A relation is given below.
{(0, 0), (2, 0.5), (4, 1), (3, 1,5), (4, 2), (5, 1.5), (6, 8)}
Which ordered pair can be removed to make this relation a function?
Why would removing this ordered pair make the relation a function?
Answers
The input and output values cannot be the same.
Hope this helps!
Related Questions
In slicing, if the end index specifies a position beyond the end of the list, Python will use the length of the list instead.
Answers
True, If the end index for slicing specifies a location after the end of the alphabet, Python will use the list's length instead.
What is slicing?
In Python, there is a concept of string, list and tuples. Sometimes it is required to access part of those string, list and tuples. This is known as slicing.
In case of slicing, suppose the the end index specifies a position beyond the end of the list, Python will return to the default length of the string. So there will be no error if the end index specifies a position beyond the end of the list.
So the above sentence is a true sentence.
To learn more about slicing, refer to the link-
https://brainly.com/question/19660645
#SPJ4
What is the range of the graph?

Answers
Answer:
D
Step-by-step explanation:
the graph is forever extending to infinity, so there's no definite range
what is 44.64 ÷ 3.6
Answers
Answer:
12.4
Step-by-step explanation:
Hope this helps :)
find the general solution of the given differential equation. y' + 5x4y = x4
Answers
\(y = (1/5) x^5 + Ce^ {(-x^5)}\) is the general solution of the given differential equation.
The given differential equation is:
y' + 5x⁴ y = x⁴
To solve this equation, we can use an integrating factor. First, we need to multiply both sides of the equation by the integrating factor, which is \(e^{(int 5x^4 dx)}\):
\(e^{(int 5x^4 dx) }y' + 5x^{4} e^{(int 5x^4 dx)} y = x^4 e^{(int 5x^4 dx)}\)
The integral of 5x⁴ is (5/5)x⁵ = x, so the integrating factor is \(e^{(x^5)}\):
\(e^{(x^5)} y' + 5x^{4} e^{(x^5)} y = x e^(x^5)\)
Now we can recognize the left-hand side as the product of the derivative of the product of \(e^{(x^5)\)and y:
\((d/dx)[e^{(x^5)} y] = x^4 e^{(x^5)}\)
Integrating both sides with respect to x, we get:
\(e^{(x^5)} y = (1/5) x^5 e^{(x^5)} + C\)
where C is the constant of integration. Dividing both sides by \(e^{(x^5)}\), we get the general solution:
\(y = (1/5) x^5 + Ce^(-x^5)\)
where C is an arbitrary constant.
\(y = (1/5) x^5 + Ce^{(-x^5)}\) is the general solution of the given differential equation.
Learn more about Integration:
https://brainly.com/question/30094386
#SPJ1
What is the value of r? r = 4 ft r = 8 ft r = 16 ft r = 32 ft.
Answers
The value of r is 4 feet, the correct option is A.
What is the area of the circle?
The area of a circle is the region occupied by the circle in a two-dimensional plane.
Given
The area of circle Z is 64 ft2.
According to the following formula, we must find the radius of the circle:
\(\rm r =\sqrt{\dfrac{Area}{\pi }}\)
Substitute all the values in the formula
\(\rm r =\sqrt{\dfrac{Area}{\pi }}\\\\\rm r =\sqrt{\dfrac{64}{3.14}}\\\\\rm r =\sqrt{20.38}\\\\r=4.5\)
Hence, the value of r is 4 feet.
To know more about the area of the circle click the link given below.
https://brainly.com/question/19164857
Which of the following shapes is the cross-section for a cone?
O A. Pentagon
O B. Square
O C. Triangle
O D. Circle
Answers
Answer:
The choose (D)
D. Circle
I hope I helped you^_^
The required cross-section for a cone is a circle. Option D is correct.
What is a conic section?A conic section is a geometric shape that is obtained by intersecting a cone with a plane. Conic sections include circles, ellipses, parabolas, and hyperbolas.
The type of conic section that is formed depends on the angle of the plane relative to the axis of the cone, as well as the distance of the plane from the vertex of the cone.
Here,
The cross-section of a cone is a circle.
A cross-section is a shape that you get when you slice a 3D object with a plane. If you slice a cone parallel to its base, you get a circle as the cross-section.
Therefore, the correct answer is option D.
Learn more about the conic section here;
https://brainly.com/question/28991363
#SPJ7
Mike uses 22 ounces of lemon juice to make one pitcher of lemonade. He has 572 ounces of lemon juice. How many pitchers of lemonade can Mike made?
Answers
22x = 572
x = 26 [pitchers of lemonade].
Answer:594
Step-by-step explanation: You have to add to find ur answer so it will be 594 ounces
Or just multiply
Rosa and her brother worked landscaping jobs last summer. Rosa earned $8 more than twice the amount earned by her brother. If their earnings totalled $71, how much did Rosa earn? NEED AN ANSWER
Answers
Explanation:
Two people Rosa & her brother
Her brother earns X
While Rosa earns 2X + 8
Now we gotta solve for X
They made $71. $71 minus X should give you Rosa’s pay
71 - X = 8 + 2X (subtract 8 from 71)
63 - X = 2X (add X to 2X)
63 = 3X (divide by 3)
21 = X
Plug in $21 for Rosa:
8 + 2(21)
8 + 42 = $50
the mean monthly electric bill for 71 residents of the local apartment complex is $62. what is the best point estimate for the mean monthly electric bill for all residents of the local apartment complex?
Answers
If the mean monthly electric bill for 71 residents of the local apartment is $62 , then the best point estimate is $62 .
In the question ,
it is given that ,
the number of residents in the local apartment complex is = 71
the mean electric bill for the 71 residents = $62 ;
we know that the sample mean is itself called as the best point estimate ;
So , best point estimate for mean monthly electric bill for all residents of local apartment complex will be = mean monthly bill for 71 residents of local apartment complex which is given as $62 .
Therefore , the best point estimate is $62 .
Learn more about Best Point Estimate here
https://brainly.com/question/19425323
#SPJ4
Please answer no links!!!!!!!!!!!

Answers
Answer:
2 (4, 14)3 (3, 5)Q4) Let x denote the time taken to run a road race. Suppose x is approximately normally distributed with a mean of 190 minutes and a standard deviation of 21 minutes. If one runner is selected at random, what is the probability that this runner will complete this road race: In less than 160 minutes? * 0.764 0.765 0.0764 0.0765 In 215 to 245 minutes? * 0.1128 O 0.1120 O 0.1125 0.1126
Answers
a. The probability that this runner will complete this road race: In less than 160 minutes is 0.0764. The correct answer is C.
b. The probability that this runner will complete this road race: In 215 to 245 minutes is 0.1125 The correct answer is C.
a. To find the probability for each scenario, we'll use the given normal distribution parameters:
Mean (μ) = 190 minutes
Standard Deviation (σ) = 21 minutes
Probability of completing the road race in less than 160 minutes:
To calculate this probability, we need to find the area under the normal distribution curve to the left of 160 minutes.
Using the z-score formula: z = (x - μ) / σ
z = (160 - 190) / 21
z ≈ -1.4286
We can then use a standard normal distribution table or statistical software to find the corresponding cumulative probability.
From the standard normal distribution table, the cumulative probability for z ≈ -1.4286 is approximately 0.0764.
Therefore, the probability of completing the road race in less than 160 minutes is approximately 0.0764. The correct answer is C.
b. Probability of completing the road race in 215 to 245 minutes:
To calculate this probability, we need to find the area under the normal distribution curve between 215 and 245 minutes.
First, we calculate the z-scores for each endpoint:
For 215 minutes:
z1 = (215 - 190) / 21
z1 ≈ 1.1905
For 245 minutes:
z2 = (245 - 190) / 21
z2 ≈ 2.6190
Next, we find the cumulative probabilities for each z-score.
From the standard normal distribution table:
The cumulative probability for z ≈ 1.1905 is approximately 0.8820.
The cumulative probability for z ≈ 2.6190 is approximately 0.9955.
To find the probability between these two z-scores, we subtract the cumulative probability at the lower z-score from the cumulative probability at the higher z-score:
Probability = 0.9955 - 0.8820
Probability ≈ 0.1125
Therefore, the probability of completing the road race in 215 to 245 minutes is approximately 0.1125. The correct answer is C.
Learn more about probability at https://brainly.com/question/32274851
#SPJ11
How patriotic are you? Would you say extremely patriotic, very patriotic, somewhat patriotic, or not especially patriotic? Below is the data from Gallup polls that asked this question of a random sample of U.S. adults in 1999 and a second independent random sample in 2010. We conducted a chi-square test of homogeneity to determine if there are statistically significant differences in the distribution of responses for these two years. In this results table, the observed count appears above the expected count in each cell. 1999 994 extremely patriotic very patriotic somewhat patriotic not especially patriotic Total 193 466 284 257.2 443.8 237.3 55.72 324 426 193 611004 259.8 448.2 239.7 517 892 477 112 1998 2010 56.28 Total Chi-Square test: Statistic DF Value P-value Chi-square 3 53.19187) <0.0001 If we included an exploratory data analysis with the test of homogeneity, the percentages most appropriate as part of this analysis for the Extremely Patriotic group are
a. 193/1517 compared to 994/1998 b. 193/1998 compared to 324/1998 c. 193/517 compared to 324/517 d. 193/994 compared to 324/1004
Answers
The appropriate percentages for the Extremely Patriotic group are 19.42% in 1999 and 32.27% in 2010, corresponding to option d: 193/994 compared to 324/1004.
To calculate the appropriate percentages for the Extremely Patriotic group, we need to compare the counts from the 1999 and 2010 samples.
In 1999:
Number of Extremely Patriotic responses: 193
Total number of respondents: 994
In 2010:
Number of Extremely Patriotic responses: 324
Total number of respondents: 1004
Now we can calculate the percentages:
Percentage for 1999: (193 / 994) × 100 = 19.42%
Percentage for 2010: (324 / 1004) × 100 = 32.27%
Therefore, the appropriate percentages as part of the exploratory data analysis for the Extremely Patriotic group are:
19.42% compared to 32.27% (option d: 193/994 compared to 324/1004).
To know more about appropriate percentages:
https://brainly.com/question/28984529
#SPJ4
PLS HELP WILL MARK BRAINLIEST!!!!!!!!
answer both questions (they are two separate questions)
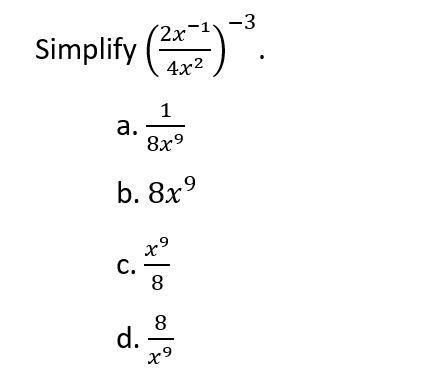

Answers
Answer:
#1
\({ \tt{ {( \frac{ {2x}^{ - 1} }{ {4x}^{2} } )}^{ - 3} }} \\ \\ = { \tt{ {( \frac{ {x}^{( - 1 - 2)} }{2}) }^{ - 3} }} \\ \\ = { \tt{ ({ \frac{ {x}^{ - 3} }{2}) }^{ - 3} }} \\ \\ = { \tt{( \frac{ {x}^{( - 3 \times - 3)} }{ {2}^{ - 3} } }}) \\ \\ ={ \boxed{ \mathfrak{answer : { \tt{ {b. \: 8 {x}^{9} }}}}}}\)
#2
\({ \tt{ \frac{16 {x}^{3} - {4x}^{2} + 44x - 60 }{4x} }} \\ \\ { \boxed{ \mathfrak{answer : \: { \tt{b. \: 4 {x}^{2} - x + 11 - \frac{15}{x} }}}}}\)
Compare
5/8 and 7/12
Answers
Answer:
to compare them, you have to get the same denominator. So you change the denominator to 24 by multipling 7/12 by 2, and 5/8 by 3. Then you have 14/24 and 15/24. This means that 5/8 is greater than 7/12
Step-by-step explanation:
Hope this helps. If you want, please mark me as brainliest
Answer: Please mark me brainlest 15
24
>
14
24
or
5
8
>
7
12
Step-by-step explanation:
Find the least common denominator or LCM of the two denominators:
LCM of 8 and 12 is 24
For the 1st fraction, since 8 × 3 = 24,
5
8
=
5 × 3
8 × 3
=
15
24
Likewise, for the 2nd fraction, since 12 × 2 = 24,
7
12
=
7 × 2
12 × 2
=
14
24
Since the denominators are now the same, the fraction with the bigger numerator is the greater fraction
Brad rolled a cube number cube 30 times and recorded the results in the tally chart below which what is the experimental probability of rolling a five
Answers
Find the derivative of the function f(x), below. It may be to your advantage to simplify before differentiating. f(x)=ln(14-e^-2x). f'(x)
Answers
The derivative of the function f(x) = ln(14 - e^(-2x)) is f'(x) = [4xe^(-2x)] / [e^(2x) - 14].
The derivative of the function f(x) = ln(14 - e^(-2x)) is given by:
f'(x) = [1/(14 - e^(-2x))] * [-2e^(-2x)]
To simplify this expression, we can factor out a -2 from the numerator:
f'(x) = [-2/(14 - e^(-2x))] * [e^(-2x)]
Now, we can use the chain rule to differentiate the second factor:
f'(x) = [-2/(14 - e^(-2x))] * [-2x e^(-2x)]
Simplifying further, we get:
f'(x) = [4xe^(-2x)] / [e^(2x) - 14]
Therefore, the derivative of f(x) is f'(x) = [4xe^(-2x)] / [e^(2x) - 14].
For more questions like Function click the link below:
https://brainly.com/question/12431044
#SPJ11
Help me on this question please

Answers
The measure of angle DAB in the given quadrilateral can be calculated as: 109°.
How to Find the Measure of an Angle in a Quadrilateral?To find the measure of an angle in a quadrilateral, you need to use the fact that the sum of all angles in a quadrilateral is always equal to 360 degrees.
Using the above fact stated, we can add up the three known angles in the given quadrilateral and then subtract it from 360 degrees to find the measure of angle DAB.
Thus, we have:
m<DAB = 360 - (90 + 97 + 64)
m<DAB = 360 - 251
m<DAB = 109°
Learn more about Quadrilateral on:
https://brainly.com/question/30291770
#SPJ1
PLEASE HELP ME IM SO CONFUSED AND THIS IS DUE IN 10 MINS!!! PLEASE HELP!!!

Answers
Answer:
The answer is 98304
Step-by-step explanation:
Which of the following statements accurately describes the expressionx +3x² - 4?A. The quotient of x+3 and x2 - 4B. The quotient of you - 4 and you - 4OC. The product of x+3 and 2 - 4OD. The product of x+3 and x+3

Answers
-Recall that the statement:
The quotient of a and b,
in algebraic notation is:
\(\frac{a}{b}\text{.}\)-Therefore, the expression:
\(\frac{x+3}{x^2-4},\)as a statement is:
The quotient of x+3 and x²-4.
Answer: Option A.
for+the+standard+normal+distribution,+how+much+confidence+is+provided+within+2+standard+deviations+above+and+below+the+mean?+95.44%+90.00%+99.74%+97.22%+99.87%
Answers
The answer to your question is that within 2 standard deviations above and below the mean of the standard normal distribution, approximately 95.44% of the data falls.
The properties of the standard normal distribution. The standard normal distribution is a bell-shaped curve with a mean of 0 and a standard deviation of 1. This distribution is important in statistics because it allows us to make comparisons and draw conclusions about different sets of data that have different means and standard deviations.
In the standard normal distribution, we can use the empirical rule, also known as the 68-95-99.7 rule, to estimate the percentage of data that falls within certain intervals of standard deviation from the mean. According to this rule, approximately 68% of the data falls within 1 standard deviation of the mean, approximately 95% falls within 2 standard deviations, and approximately 99.7% falls within 3 standard deviations.
Therefore, we can conclude that within 2 standard deviations above and below the mean of the standard normal distribution, approximately 95.44% of the data falls. This is because 2 standard deviations above and below the mean cover approximately 95.44% of the total area under the curve.
To know more about standard deviation visit:
https://brainly.com/question/23907081
#SPJ11
Prove that among a group of six students, at least two received the same grade on the final exam. (The grades assigned were chosen from A,B,C,D,F.)A,B,C,D,F.)
Answers
Among a group of six students, at least two received the same grade on the final exam.
This problem is a classic example of the Pigeonhole Principle, which states that if there are more pigeons than pigeonholes, then at least one pigeonhole must contain more than one pigeon. In this case, the pigeons are the grades assigned to the six students, and the pigeonholes are the possible grades they could have received (A, B, C, D, or F).
Since there are five possible grades and six students, at least one grade must have been assigned to two or more students. This is because if each student received a different grade, there would be five grades in total, which is one less than the number of students, so at least one grade must be repeated.
learn more about Pigeonhole Principle,
https://brainly.com/question/30322724
#SPJ4
Answer need ASAP
Add -3 1/6 + 5 3/4 and write it as a reduced mixed number
-3 1/6 + 5 3/4 = ?
Answers
Answer: 2 5/6 I think.
Wait no. I just did the math and it would be 2 1/2
A bolt manufacturer is very concerned about the consistency with which his machines produce bolts. The bolts should be 0.2 centimeters in diameter. The variance of the bolts should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level? Step 1 of 5: State the hypotheses in terms of the standard deviation. Round the standard deviation to four decimal places when necessary. A bolt manufacturer is very concerned about the consistency with which his machines produce bolts. The bolts should be 0.2 centimeters in diameter. The variance of the bolts should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level? Step 2 of 5: Determine the critical value(s) of the test statistic. If the test is twotailed, separate the values with a comma. Round your answer to three decimal places. A bolt manufacturer is very concerned about the consistency with which his machines produce boits. The bolts should be 0.2 centimeters in diameter. The variance of the boits should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level?
Answers
To determine if the bolts vary by more than the required variance, we can conduct a hypothesis test. The null hypothesis (H₀) states that the variance of the bolts is equal to or less than the required variance (σ² ≤ 0.025), while the alternative hypothesis (H₁) states that the variance is greater than the required variance (σ² > 0.025).
Next, we need to determine the critical value(s) of the test statistic. Since we are testing for variance, we will use the chi-square distribution. For a one-tailed test with α = 0.01 and 14 degrees of freedom (n-1), the critical value is 27.488.
Now, we can compare the test statistic to the critical value. The test statistic is calculated as (n-1) * s² / σ², where n is the sample size (15), s² is the sample variance (0.1587²), and σ² is the required variance (0.025).
If the test statistic is greater than the critical value, we reject the null hypothesis and conclude that the bolts vary by more than the required variance. Otherwise, we fail to reject the null hypothesis.
To learn more about Hypothesis test - brainly.com/question/29996729
#SPJ11
To determine if the bolts vary by more than the required variance, we can conduct a hypothesis test. The null hypothesis (H₀) states that the variance of the bolts is equal to or less than the required variance (σ² ≤ 0.025), while the alternative hypothesis (H₁) states that the variance is greater than the required variance (σ² > 0.025).
Next, we need to determine the critical value(s) of the test statistic. Since we are testing for variance, we will use the chi-square distribution. For a one-tailed test with α = 0.01 and 14 degrees of freedom (n-1), the critical value is 27.488.
Now, we can compare the test statistic to the critical value. The test statistic is calculated as (n-1) * s² / σ², where n is the sample size (15), s² is the sample variance (0.1587²), and σ² is the required variance (0.025).
If the test statistic is greater than the critical value, we reject the null hypothesis and conclude that the bolts vary by more than the required variance. Otherwise, we fail to reject the null hypothesis.
To learn more about Hypothesis test - brainly.com/question/29996729
#SPJ11
Which of the following functions of x is guaranteed by the Extreme Value Theorem to have an absolute maximum on the interval [0,4]? a. y=tanx
b. y=tan−1x
c. y=x^2−16/x^2+x−20
d. y=1/e^x-1
Answers
We need to identify the function among the given options which is guaranteed by the Extreme Value Theorem to have an absolute maximum on the interval [0,4].What is the Extreme Value Theorem? The extreme value theorem says that a function on a closed interval must have a maximum and a minimum value.
The correct option is-C
In other words, there is an absolute maximum and an absolute minimum value. It is an important theorem in calculus. Let's check the given options for the absolute maximum on the interval [0,4]:a. y=tanx As the function
f(x)=tanx is not continuous on the interval [0,4], it is not guaranteed to have an absolute maximum on the interval [0,4]. Therefore, option a is incorrect .b
. y=tan⁻¹xAs the function
f(x)=tan⁻¹x is not continuous on the interval [0,4], it is not guaranteed to have an absolute maximum on the interval [0,4].
Therefore, option b is incorrect. c.
y=x²−16/x²+x−20 Let's check the critical points of the function
f(x)=x²−16/x²+x−20 by finding its derivative and equating it to zero:
f '(x)= (2x(x² - 20) + (x² - 16)(2x + 1))/ (x² + x - 20)²=0On solving this equation,
we get x=-4, 0, and 4. Now we will check the function values of these critical points as well as at the endpoints of the given interval:[0,4]. We get: f(0) = -4 and
f(4) = 4/3 Since f(4) is greater than all other values, the absolute maximum of f(x) is at
x=4.Therefore, option c is correct .d. y=1/e^x-1As the function f(x)=1/e^x-1 is not continuous on the interval [0,4], it is not guaranteed to have an absolute maximum on the interval [0,4].
To know more about function visit:
https://brainly.com/question/30721594
#SPJ11
write an equation of line parallel to the line y=2/5x+10 and passes through the point 10/11
Answers
Answer: y=2/5x+b
Step-by-step explanation:
Find the Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) for the curve →r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0. Round answers to 3 decimal places.
T(0) =0=[sqrt(89)= sqrt(89)]
N(0) =[ ]
B(0) =[ ]
Answers
The tangent vector → \(r(t)=〈4cos(2t),4sin(2t),5t〉\), normal vector at t=0 is given by →N(0) = 〈-1,0,0〉, and binormal vector at t=0 is given by →\(B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector, normal vector, and binormal vector of the given curve are as follows:
Given curve:
→ \(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0
To find: Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) at the point t=0
Tangent vector: To find the tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0,
we need to differentiate the equation of the curve with respect to t.t = 0, we have:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉→r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
Differentiating w.r.t t:→\(r(t) = 〈4cos(2t),4sin(2t),5t〉 → r'(t) = 〈-8sin(2t),8cos(2t),5〉t = 0\),
we have:
→\(r'(0) = 〈-8sin(0),8cos(0),5〉= 〈0,8,5〉\)
Therefore, the tangent vector at t = 0 is given by
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Normal vector:To find the normal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to differentiate the equation of the tangent vector with respect to t.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating w.r.t t:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉t = 0\),
we have:
→\(T'(0) = 〈-16cos(0),-16sin(0),0〉= 〈-16,0,0〉\)
Therefore, the normal vector at t = 0 is given by
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Binormal vector: To find the binormal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to cross-product the equation of the tangent vector and normal vector of the curve.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉\)
The cross product of two vectors:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the binormal vector at t = 0 is given by→B(0) = 〈0, -0.441, -0.898〉
Hence, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are as follows:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The given curve is
→\(r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0.\)
We are asked to find the tangent vector, the normal vector, and the binormal vector of the given curve at t=0.
the tangent vector at t=0. To find the tangent vector, we need to differentiate the equation of the curve with respect to t. Then, we can substitute t=0 to find the tangent vector at that point. the equation of the curve Is:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉\)
At t = 0, we have:
→\(r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
We can differentiate this equation with respect to t to get the tangent vector as:
→\(r'(t) = 〈-8sin(2t),8cos(2t),5〉\)
At t=0, the tangent vector is:
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Next, we find the normal vector. To find the normal vector, we need to differentiate the equation of the tangent vector with respect to t. Then, we can substitute t=0 to find the normal vector at that point.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating this equation with respect to t, we get the normal vector as:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉\)
At t=0, the normal vector is:
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Finally, we find the binormal vector. To find the binormal vector, we need to cross-product the equation of the tangent vector and the normal vector of the curve.
At t=0, we can cross product →T(0) and →N(0) to find the binormal vector.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
The normal vector is:
→N(0) = 〈-1,0,0〉Cross product of two vectors →T(0) and →N(0) is given as:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0 is given by →\(T(0) = 〈0.000,0.898,0.441〉.\)
The normal vector at t=0 is given by →N(0) = 〈-1,0,0〉.
The binormal vector at t=0 is given by →B(0) = 〈0, -0.441, -0.898〉.
To know more about binormal vectors visit
brainly.com/question/31673319
#SPJ11
whats 0.00316 in scientific notation ?
Answers
(scientific notation)
= 0.00316
(real number)
The temperature on Monday was -23° F. The temperature on Tuesday was 18° higher. What was the temperature on Tuesday?
A.
-41° F
B.
5° F
C.
-5° F
D.
41° F
Answers
Answer: C is correct
Step-by-step explanation:
-23+18= -5
In the country of United States of Heightlandia, the height measurements of ten-year-old children are approximately normally distributed with a mean of 56.9 inches, and standard deviation of 8.2 inches. A) What is the probability that a randomly chosen child has a height of less than 42.1 inches? Answer= (Round your answer to 3 decimal places.) B) What is the probability that a randomly chosen child has a height of more than 41.7 inches?
Answers
A) The probability that a randomly chosen child has a height of less than 42.1 inches is 0.036 (rounded to 3 decimal places).B)The probability that a randomly chosen child has a height of more than 41.7 inches is 0.966 (rounded to 3 decimal places).
A) In order to find the probability that a randomly chosen child has a height of less than 42.1 inches, we need to find the z-score and look up the area to the left of the z-score from the z-table.z-score= `(42.1-56.9)/8.2 = -1.8098`P(z < -1.8098) = `0.0359`
Therefore, the probability that a randomly chosen child has a height of less than 42.1 inches is 0.036 (rounded to 3 decimal places).
B) In order to find the probability that a randomly chosen child has a height of more than 41.7 inches, we need to find the z-score and look up the area to the right of the z-score from the z-table.z-score= `(41.7-56.9)/8.2 = -1.849`P(z > -1.849) = `0.9655`.
Therefore, the probability that a randomly chosen child has a height of more than 41.7 inches is 0.966 (rounded to 3 decimal places).
Note: The sum of the probabilities that a randomly chosen child is shorter than 42.1 inches and taller than 41.7 inches should be equal to 1. This is because all the probabilities on the normal distribution curve add up to 1
Learn more about probability here,
https://brainly.com/question/13604758
#SPJ11
find the perimeter
A. 8cm
B.34 cm
C.32 cm
D.49 cm
the bottom number is 10 in the photo

Answers
Answer:
The answer is number B:34 cm
The bottom is 10, 10 - 3 - 3 (the sides on top) = 4 so we know the middle part is 4.
We know that both of the "small ups" are 2 and the "longer ups" are 5.
Adding this altogether we get:
3 + 3 + 2 + 2 + 4 + 10 + 5 + 5 =
6 + 4 + 4 + 10 + 10 =
10 + 4 + 20 =
14 + 20 =
= 34
So our answer is B. 34 cm
Hope this helps, have a nice day! :D
(I answered in the comments, but one was deleted so I am answering this here too!)