A rock-climbing wall at a local park has a right triangular section that slants toward the climber, as shown in the picture below. The height of the wall is 5 meters and the slanted section begins 1.2 meters up the wall at an angle of 14 degrees.

Answers
The length of the hypotenuse section on the rock-climbing wall at the local park is 3.92 meters
Calculating the length of the hypotenuse sectionThe length of the hypotenuse section is calculated using the following cosine function
cos(14) = adjacent/hypotenuse
Substitute the known values in the above equation, so, we have the following representation
cos(14) = (5 - 1.2)/hypotenuse
This gives
hypotenuse = (5 - 1.2)/cos(14)
Evaluate
hypotenuse = 3.92 meters
Hence, the hypotenuse is 3.92 meters
Read more about right triangles at
brainly.com/question/2437195
#SPJ1
Related Questions
what’s the working out to this question as i know the answer is 2.94cm squared but the working out is wrong!

Answers
Answer:
2.94
Step-by-step explanation:
A = 6a²
6 × .7² = 2.94
.7 × .7 = .49
6 × .7 = 2.94
\( a = 6a {}^{2} \)
a is the side
area -6 x 0.7
Aris and Josiah are reading a 50-page book for their ELA class. Aris wants to know what page Josiah is reading. Josiah gives her two hints: 1. The product of the two page numbers he can see is 930. 2. The page he is reading is an odd numbered page.
Answers
Answer:
31
Step-by-step explanation:
Let x and (x + 1) be the page numbers Josiah can see
Hint 1: x(x + 1) = 930
⇒ x² + x = 930
⇒ x² + x - 930 = 0
Using quadratic formula,
\(x = \frac{-b\pm\sqrt{b^2 -4ac} }{2a}\)
a = 1, b = 1 and c = -930
\(x = \frac{-1\pm\sqrt{1^2 -4(1)(-930)} }{2(1)}\\\\= \frac{-1\pm\sqrt{1 +3720} }{2}\\\\= \frac{-1\pm\sqrt{3721} }{2}\\\\= \frac{-1\pm61 }{2}\\\)
\(x = \frac{-1-61 }{2}\;\;\;\;or\;\;\;\;x= \frac{-1+61 }{2}\\\\\implies x = \frac{-62 }{2}\;\;\;\;or\;\;\;\;x= \frac{60 }{2}\\\\\implies x = -31\;\;\;\;or\;\;\;\;x= 30\)
Sice x is a page number, it cannot be negative
⇒ x = 30 and
x + 1 = 31
The two pages Josiah can see are pg.30 and pg.31
Hint 2: The page he is reading is an odd number
Out of the pages 30 and 31, 31 is an odd number
Thereofre, Josiah is reading page 31
9) What 2 numbers have a total of 28 and a difference of 6?
Answers
Answer:
Sum: 17 + 11 = 28
Difference: 17 - 11 = 6
Step-by-step explanation:
The sum of x and y is 28. In other words, x plus y equals 28 and can be written as equation A:
x + y = 28
The difference between x and y is 6. In other words, x minus y equals 6 and can be written as equation B:
x - y = 6
Now solve equation B for x to get the revised equation B:
x - y = 6
x = 6 + y
Then substitute x in equation A from the revised equation B and then solve for y:
x + y = 28
6 + y + y = 28
6 + 2y = 28
2y = 22
y = 11
Now we know y is 11. Which means that we can substitute y for 11 in equation A and solve for x:
x + y = 28
x + 11 = 28
X = 17
Summary: The sum of two numbers is 28 and their difference is 6. What are the two numbers? Answer: 17 and 11 as proven here:
Sum: 17 + 11 = 28
Difference: 17 - 11 = 6
Answer:
17 +11 = 28
hope this helps
What’s the correct answer for this question?
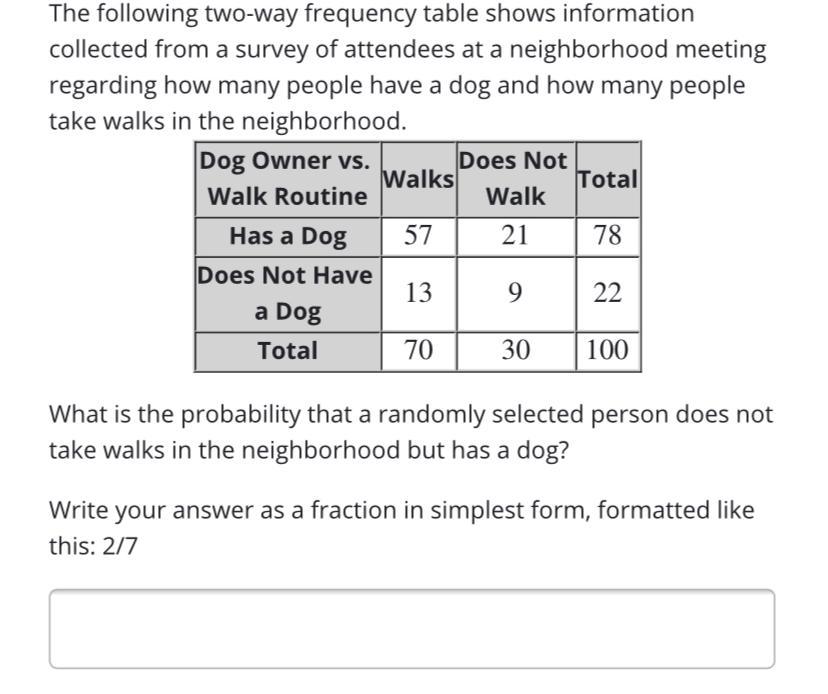
Answers
Answer:
21/100
Step-by-step explanation:
By looking at the table, we can find the box that has information on people who have dogs but do not walk. The number is 21. The total number of people is 100. To find probability, divide 21 by 100.
21/100
This fraction is in its simplest form and cannot be simplified any further.
What kind of slopes do you need to have for a square?
Answers
pls help me pls pls pleasse

Answers

6x - y = 5
3x + y = 4
Answers
Answer:
1.6x-y=5--->equ.(i)
3x+4=y--->equ.(ii)
substitution method
6x-y=5
y=5+6x--->equ (iii)
Replace y=5+6x into equ--->(ii)
3x-5+6x=4
3x+6x=4+5
9x=9
divide both side by 9
9x/9=9/9
x=1
Replace x=1 into equ (iii)
6(1)-y=5
6-y=5
y=5+6
y=11
then your x and y is
x=1,y=11
HELP PLS IK ITS NOT C JUST REWRITING IT WITHIUT PARENTHESIS

Answers
Answer:
Wouldn't it be answer B?
Step-by-step explanation:
The rest of the answers have addition which is not in the problem provided.
I need a good answer, with a good explanation.
Janie and Jasmine are playing three games at an arcade. Each of the games requires either 2, 3, or 4 tokens. The girls plan to play as many games as they can before running out of tokens.
Write an expression to represent the total number of tokens that Janie and Jasmine will need to play each of the three games at least once. Let m represent the number of games that require 2 tokens; n represent the number of games that require 3 tokens; p represent the number of games that require 4 tokens.
Answers
The expression to represent the information will be 2(2m + 3n + 4p)
How to illustrate the expression?From the information given, Janie and Jasmine are playing three games at an arcade. Each of the games requires either 2, 3, or 4 tokens.
There are m number of games required.
There are n number of games that require 3 token.
Therefore, the expression to represent the information will be:
= 2(2 × m) + 2(3 × n) + 2(4 × p)
= 2(2m + 3n + 4p)
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
Answer:
The other person who answered is incorrect!! The real answer is 2m + 3n + 4p
Step-by-step explanation:
have a good besti!!!!
-leeknowishawt
Which of the following is the product of the rational expressions shown below?


Answers
Answer:
A
Step-by-step explanation:
\($\frac{x-3}{x+5} \cdot \frac{3x}{x-5} $\)
\($\frac{3x(x-3)}{(x+5)(x-5)} $\)
\($\frac{3x^2-9x}{x^2-25} $\)
\(\dfrac{(3x^2-9x)}{(x^2-25)}\)
What is rational function?A rational function is defined as a polynomial divided by a polynomial.
What are Fractions?Fractions is defined as a numerical value that represents a portion of a whole is used to represent fractions. A fraction is a component or section taken from a whole, which can be any number, a certain amount, or an object.
\((\dfrac{x-3}{x+5})(\dfrac{3x}{x-5} )\\\)
\(\dfrac{(x-3)(3x)}{(x+5)(x-5)}\)
Used formula a² - b² = (a + b)(a - b)
\(\dfrac{(3x^2-9x)}{(x^2-5^2)}\)
\(\dfrac{(3x^2-9x)}{(x^2-25)}\)
learn more about rational function here:
brainly.com/question/20850120
#SPJ2
Which of the following is a characteristic of a plane
Answers
Answer:
I think you meant to add a list of answers but didn't so here's the characteristics of a plane: Flat, two dimensional, extends infinitely, and is assembled about multiple points and lines.
Step-by-step explanation:
Answer:
If you are taking the FLVS test it is "Two endpoints"
Step-by-step explanation:
Just took the test
hope it helps :)
A college student takes the same number of credits each semester. They had 8 credits when they started, and after 5 semesters, they had 58 credits.
Which of these expresses the rate at which they is earning credits?
Answers
Answer:
There are 10 credits per semester.
Step-by-step explanation:
Given that: A college student takes the same number of credits each semester.
They had 8 credits when they started, and after 5 semesters, they had total 58 credits.
Now, In which rate they are earning credits per semester,
for that use the formula:
\(rate=\frac{change of credits}{total no of semeters}\)
rate=50/5
The change in credits is 58-8 = 50, since the
student earned 50 credits in 5 semesters.
So the rate at which they are earning credits per semester is:
Rate = 10 credits per semester.
Hence, there are 10 credits per semester.
Learn more about rates & ratios, refer here:
https://brainly.com/question/12024093
Need help with this math problem please!!

Answers
Answer:
The domain of a function is the set of numbers for which the function is defined.
Here, this function has values of number from -1 to +3
therefore, it's domain is [-1,3]
The range is the set of results of a function
here, this function ranges between -5 to +4
therefore, its range is [-5,4]
I am 1 Brainly away from Virtuoso, help if you find this answer helpful
Find the height of the tower using the information given in the illustration.

Answers
using SOH CAH TOA
Tan 85.144 =h/130
h=tan 85.144*130
h=1530.19 fr

Solve the inequality for x:
8 + 4(x - 3) + 3x < 24
Answers
Answer:
7x - 4 < 24
Step-by-step explanation:
8 + 4x - 12 + 3x < 24
3x + 4x - 12 + 8 < 24
7x - 4 < 24
Hope this helps!
Have a nice day!
If you find my answer helpful
Pls consider marking my answer as Brainliest! It would mean a lot!
Answer:
8 + 4x - 12 + 3x < 24
3x + 4x - 12 + 8 < 24
7x - 4 < 24
Step-by-step explanation:
On Joe's bookshelf are: • 8 fiction books 3 non-fiction books • 4 historical drama books Joe will randomly choose 1 book to read from the shelf. What is the probability that he will choose a non-fiction book? A)0.267 B)0.8 C)0.2 D)0.533
Answers
Answer:
There is a 0.2 chance or 20% change that he will choose a nonfiction book. PLease mark as helpful if it is! thanks
Suppose a baker claims that the average bread height is more than 15cm. Several of this customers do not believe him. To persuade his customers that he is right, the baker decides to do a hypothesis test. He bakes 10 loaves of bread. The mean height of the sample loaves is 17 cm with a sample standard deviation of 1.9 cm. The heights of all bread loaves are assumed to be normally distributed. The baker is now interested in obtaining a 95% confidence interval for the true mean height of his loaves. What is the lower bound to this confidence interval? 2 cm (round to 2 decimal places) What is the upper bound to this confidence interval? cm (round to 2 decimal places) For the following situations, use RStudio to find the appropriate t-critical values that would be needed to construct a confidence interval. Round all critical values to the second decimal place. 1. n = 15, confidence level is 95%, x= 35 and s = 2.7, t-critical value- 2, n = 37, confidence level is 99%, x= 82 and s = 5.9 t-critical value- 2 3, n 1009, confidence level is 90%, x 0.9 and s-0.04 t- critical value = 2 2
Answers
The correct answer is Confidence interval lower bound: 32.52 cm,Confidence interval upper bound: 37.48 cm
To calculate the confidence interval for the true mean height of the loaves, we can use the t-distribution. Given that the sample size is small (n = 10) and the population standard deviation is unknown, the t-distribution is appropriate for constructing the confidence interval.
The formula for a confidence interval for the population mean (μ) is:
Confidence Interval = sample mean ± (t-critical value) * (sample standard deviation / sqrt(sample size))
For the first situation:
n = 15
Confidence level is 95% (which corresponds to an alpha level of 0.05)
x = 35 (sample mean)
s = 2.7 (sample standard deviation)
Using RStudio or a t-table, we can find the t-critical value. The degrees of freedom for this scenario is (n - 1) = (15 - 1) = 14.
The t-critical value at a 95% confidence level with 14 degrees of freedom is approximately 2.145.
Plugging the values into the formula:
Confidence Interval = 35 ± (2.145) * (2.7 / sqrt(15))
Calculating the confidence interval:
Lower Bound = 35 - (2.145) * (2.7 / sqrt(15)) ≈ 32.52 (rounded to 2 decimal places)
Upper Bound = 35 + (2.145) * (2.7 / sqrt(15)) ≈ 37.48 (rounded to 2 decimal places)
Therefore, the lower bound of the confidence interval is approximately 32.52 cm, and the upper bound is approximately 37.48 cm.
For the second situation:
n = 37
Confidence level is 99% (which corresponds to an alpha level of 0.01)
x = 82 (sample mean)
s = 5.9 (sample standard deviation)
The degrees of freedom for this scenario is (n - 1) = (37 - 1) = 36.
The t-critical value at a 99% confidence level with 36 degrees of freedom is approximately 2.711.
Plugging the values into the formula:
Confidence Interval = 82 ± (2.711) * (5.9 / sqrt(37))
Calculating the confidence interval:
Lower Bound = 82 - (2.711) * (5.9 / sqrt(37)) ≈ 78.20 (rounded to 2 decimal places)
Upper Bound = 82 + (2.711) * (5.9 / sqrt(37)) ≈ 85.80 (rounded to 2 decimal places)
Therefore, the lower bound of the confidence interval is approximately 78.20 cm, and the upper bound is approximately 85.80 cm.
For the third situation:
n = 1009
Confidence level is 90% (which corresponds to an alpha level of 0.10)
x = 0.9 (sample mean)
s = 0.04 (sample standard deviation)
The degrees of freedom for this scenario is (n - 1) = (1009 - 1) = 1008.
The t-critical value at a 90% confidence level with 1008 degrees of freedom is approximately 1.645.
Plugging the values into the formula:
Confidence Interval = 0.9 ± (1.645) * (0.04 / sqrt(1009))
Learn more about Confidence interval here:
https://brainly.com/question/15712887
#SPJ8
what is 2/3(9+x)=-5(4-x)
Answers
Answer:
x=78
Step-by-step explanation:
2/3(9+x)=-5(4-x)
6+2/3=-20+x
6=-20+1/3x
x=78
Answer:
x=6
Step-by-step explanation:
Distribute.
2/3 * 9 = 6
2/3 * x = 2/3x
Distribute other side.
-5*4 = -20
-5 * -x = 5x
Rewrite.
6 + 2/3x = -20 + 5x
Subtract 5x from both sides.
-13/3x + 6 = -20
Subtract 6 from both sides.
-13/3x = -26
Multiply -3/13 to both sides.
x=6
Can someone help me with this.. It is timed I WILL MARK YOU AS BRAINLIEST

Answers
Answer:
1) dividend
2) divisor
3) quotient
4.1 A bag contains 6 red, 4 green, 2 yellow and 3 blue balls. In each case, give the ratio (in simplest form) of the asked number of balls in the bag.( 4 ) 4.1.1 The number of red balls to the number of green balls.
Answers
The number of red balls to the number of green balls is 3 : 2
How to determine the ratio?The distribution of the balls is given as:
6 red, 4 green, 2 yellow and 3 blue balls
The number of red balls to the number of green balls is represented as:
Ratio = Red : Green
So, we have:
Ratio = 6 : 4
Simplify
Ratio = 3 : 2
Hence, the number of red balls to the number of green balls is 3 : 2
Read more about ratios at:
https://brainly.com/question/2328454
#SPJ1
Find the domain and range of the relation. Also determine whether the relation is a function.
{(6,3), (8,5), (-4,-4), (5,5)}
Answers
The domain is:
D: {-4, 5, 6, 8}
The range is:
R: {-4, 3, 5}
And yes, the relation is a function.
How to determine the domain and range?
For a relation that maps elements x into elements y (in the form (x, y)), we define the domain as the set of the inputs (values of x) and the range as the set of the outputs (values of y).
Here our relation is defined by: {(6,3), (8,5), (-4,-4), (5,5)}
The domain is the set of the first values of each pair, so we have:
D: {-4, 5, 6, 8}
The range is the set of the second values of each pair:
R: {-4, 3, 5}
Now, is this a function?
Yes, it is a function, because each input is mapped into only one output.
If you want to learn more about domain and range:
https://brainly.com/question/10197594
#SPJ1
Which system is represented in the graph? y > x2 – 3x + 2y ≥ –x2 + 1 y < x2 – 3x + 2y < –x2 + 1 y ≥ x2 – 3x + 2y ≤ –x2 + 1 y > x2 – 3x + 2y < –x2 + 1

Answers
Explanation
To find the answer, we will have to find the equations that define the two functions
For the first graph
\(\begin{gathered} let \\ f(x)=a(x+1)(x-1) \\ when\text{ } \\ x=0,\text{ y=1} \\ 1=a(1)(-1) \\ a=-1 \\ Thus \\ y\ge-1(x^2-1) \\ y\ge-x^2+1 \end{gathered}\)For the second graph (The purple)
\(\begin{gathered} g(x)=a(x-1)(x-2) \\ when\text{ x=0,y=2} \\ 2=a(0-1)(0-2) \\ a=\frac{2}{-1\times-2}=\frac{2}{2}=1 \\ \\ a=1 \\ Thus,\text{ we have} \\ g(x)>1(x-1)(x-2) \\ g(x)>x^2-3x+2 \\ y>x^2-3x+2 \end{gathered}\)Thus, the answer is
\(\begin{gathered} y\ge-x^2+1 \\ y>x^2-3x+2 \end{gathered}\)In a class of 80 Students, 30 offered mathematics, 20 offered Accountancy and 40 offered Economics. Those who offered both mathematics and accountancy are more than those who offered both Accountancy and Economics by 2. No student offered all the subjects and none offered both mathematics and Economics. Find the number of students who offered Accountancy only?
Answers
The number of students who offered Accountancy only is 10.
Let's represent the number of students who offered Mathematics as M, the number of students who offered Accountancy as A, and the number of students who offered Economics as E.
From the given information:
M = 30 (Number of students who offered Mathematics)
A = 20 (Number of students who offered Accountancy)
E = 40 (Number of students who offered Economics)
We are also given the following conditions:
M ∩ A > A ∩ E by 2
M ∩ E = 0
We know that the total number of students is 80, so:
M + A + E = 80
Now, let's solve for the number of students who offered Accountancy only.
We can start by substituting the given values into the equation:
30 + 20 + 40 = 80
Now, we need to find the value of A ∩ E (Number of students who offered both Accountancy and Economics).
Since none offered both Mathematics and Economics, we can subtract M from A:
A - M = A ∩ E
20 - 30 = A ∩ E
-10 = A ∩ E
Since A ∩ E cannot be a negative number, we know that A ∩ E = 0.
Now, let's use the first condition: M ∩ A > A ∩ E by 2.
Substituting the values, we have:
M ∩ A - A ∩ E = 2
M ∩ A - 0 = 2
M ∩ A = 2
Now, we can substitute the values of M ∩ A and M into the equation M + A + E = 80:
30 + A + 40 = 80
A + 70 = 80
A = 10
For more such question on Accountancy visit:
https://brainly.com/question/28569477
#SPJ8
Please look at the photo. Thank you.

Answers
The output value of (f∘g)(x) is: \((f \circ g)(x) = \frac{4x^2-29x+60}{x +3}\)
The domain of (f∘g)(x) is (-∞, -3) U (-3, ∞).
How to determine the corresponding output value for this function?In this scenario, we would determine the corresponding composite function of f(x) and g(x) under the given mathematical operations (multiplication) in simplified form as follows;
\(f(x) = \frac{x-6}{x +3}\)
g(x) = 4x - 15
Next, we would write the numerators and denominators in factored form as follows;
(x - 6)(4x - 15)
4x² - 15x - 24x + 60
4x² - 29x + 60
Now, we can derive the corresponding composite function of f(x) and g(x);
\((f \circ g)(x) = \frac{4x^2-29x+60}{x +3}\)
For the restrictions on the domain, we would have to equate the denominator of the rational function to zero and then evaluate as follows;
x + 3 ≠ 0
x ≠ -3
Domain = (-∞, -3) U (-3, ∞).
Read more on domain here: brainly.com/question/17440903
#SPJ1
The longest side of a triangle is 4 inches longer than the shortest side. The medium side is 3 inches longer than the shortest side. If the perimeter of the triangle is 25 inches, what are the lengths of the 3 sides
Answers
Answer:
Longest side = 10 inches
Medium side = 9 inches
Shortest side = 6 inches
Step-by-step explanation:
Let the longest side be L, the medium side be M and the shortest side be S
From the data,
L = S + 4
(The longest side of a triangle is 4 inches longer than the shortest side)
M = S + 3
(The medium side is 3 inches longer than the shortest side)
Perimeter of the triangle
P = L + M + S
Substituting for L and M in terms of S:
P = (S + 4) + (S + 3) + S
P = S + S + S + 4 + 3
P = 3S + 7
We are given that perimeter P = 25 inches
So,
3S + 7 = 25
Subtract 7 from both sides
3S = 25-7 = 18
Divide by 3 both sides:
3S/3 = 18/3
S = 6
So shortest side is 6 inches
Longest side L = 6 + 4 = 10 inches
Medium side M = 6 + 3 = 9 inches
What is the meaning of "\(F=\left \{ (x,y):\varphi (x,y,p) \right \}\)"?
![What is the meaning of "[tex]F=\left \{ (x,y):\varphi (x,y,p) \right \}[/tex]"?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qPezzQZ7dJhdA0YcETQG5fBdyZW4BfQR.png)
Answers
The expression "F = {(x, y) : φ(x, y, p)}" represents a set of ordered pairs (x, y) that satisfy a condition defined by the function φ. The interpretation and nature of the set F depend on the specific function φ and the parameter p, which determine the relationship between the variables x, y, and p.
The expression "F = {(x, y) : φ(x, y, p)}" represents a set F consisting of ordered pairs (x, y) that satisfy a particular condition defined by the function φ, which takes the variables x, y, and p as inputs.
To fully understand the meaning of F, we need to delve into the function φ and its relationship with the variables x, y, and p. The function φ could represent a wide range of mathematical relationships or conditions that determine the inclusion of certain pairs (x, y) in the set F.
For instance, let's consider a specific example where vraphi(x, y, p) is defined φ(x, y, p) = \(x^2 + y^2 - p^2.\)In this case, F = {(x, y) : \(x^2 + y^2 - p^2\)= 0} represents a set of ordered pairs (x, y) that satisfy the equation \(x^2 + y^2 - p^2 = 0.\) This equation represents a circle with radius p centered at the origin (0, 0). Consequently, F corresponds to all the points lying on the circumference of this circle.
It is important to note that the specific meaning and implications of F heavily rely on the nature of the function φ and the parameter p. Different functions and parameters will yield distinct sets F with their own unique characteristics and interpretations.
For more such information on: expression
https://brainly.com/question/28602085
#SPJ8
Leila triples her recipe that calls for 2/5 of a cup of flour. Leila has 1 cup of flour. Does she have enough to triple her recipe?
no
yes
Answers
Answer:
No
Step-by-step explanation:
3 × \(\frac{2}{5}\) = \(\frac{6}{5}\) = 1 \(\frac{1}{5}\) cups required to triple her recipe
she only has 1 cup
so does not have enough to triple her recipe
Answer:
No
Step-by-step explanation:
If she triples it that means you need to triple the 2/5 so she would neew 6/5 of flour which is 1/5 more than what she has.
“One subtracted from the product of 4 and a number is 1 1”
Answers
Answer:
3
Step-by-step explanation:
4x3=12
12-1=11
Jason works for a car dealer and his commission for selling a car is 2% of the selling price. Jason sold two cars last month for $70,000 and $60,000. how much commission in total did Jason receive?
Answers
Answer:
$2600
Step-by-step explanation:
2/100×70000=1400
2/100×60000=1200
1400+1200=2600
In Problems 21 through 30, set up the appropriate form of a
particular solution yp, but do not determine the values of the
coefficients.y" – 2y' + 2y = et sin x = . =
Answers
The particular solution of Differential equation y" – 2y' + 2y = et sin x is yp = (1/2et - 1/2et cos(x))sin(x).
We assume the particular solution is of the form of given differential equation is
yp = (Aet + Bcos(t))sin(x) + (Cet + Dsin(t))cos(x)
where A, B, C, and D are constants to be determined.
Taking the first and second derivative of yp with respect to t:
yp' = Aet sin(x) - Bsin(t)sin(x) + Cet cos(x) + Dcos(t)cos(x)
yp'' = Aet sin(x) - Bcos(t)sin(x) - Cet sin(x) + Dsin(x)cos(t)
Substituting these into the differential equation and simplifying, we get:
(et sin x) = (A - C)et sin(x) + (B - D)cos(x)sin(t)
Since et sin x is not a solution to the homogeneous equation, the coefficients of et sin x and cos(x)sin(t) on both sides of the equation must be equal. Therefore:
A - C = 1 and B - D = 0
Solving for A, B, C, and D, we get:
A = 1/2, B = 0, C = -1/2, D = 0
So the particular solution is:
yp = (1/2et - 1/2et cos(x))sin(x)
To know more about Differential Equation:
https://brainly.com/question/2273154
#SPJ4