A room is 15 by 20 feet with a 9 foot celling. How much would it cost to paint all the walls if a gallon of paint cost $23.45 and covers about 250 square feet?
Answers
Answer:
$70.35 (3 cans)
Step-by-step explanation:
2 walls at 15' x 9' = 270 ft^2
2 walls at 20' x 9' = 360 ft^2
Total area = 630 ft^2
Total cost = (630 ft^2)*($23.45/250 ft^2) = $59.09
But we need to assume that we need to purchase whole gallons, not fractions of a can.
Each can covers 250 ft^2, so we'll need 3 can (750 ft^2) since 2 (500 ft^2) won't cover everything.
3 cans at $23.45 each is $70.35
Related Questions
PLEASE PLEASE PLEASE HELPPPPPPPPPPPPP


Answers
Answer:
1) B
2) B
Step-by-step explanation:
1) funtion 1 slope is 4
function 2 we use y2-y1/x2-x1
10-6/3-1
4/2
2 is the slope of function 2
so function 1 is bigger
1) only b is correct because it lands on the same line of y=x
hopes this helps please mark brainliest
Lorena's backpack has a mass of 15,000 grams.
What is the mass of Lorena's backpack in kilograms?
Lorena's backpack weighs
kilograms.
Answers
Answer:
1 kg = 1000 grams
15,000 grams = 15kg
What is the measure of angle y in this figure?

Answers
Step-by-step explanation:
180-163= 17
163+17=180
x and z = 17
y=163
SOMEONE PLEASE HELP
Describe how the variable h and the variable k of the general formula for a cube root function effects the graph. The general formula is y=a^3sqrt x-h+k
Answers
Using translation concepts, it is found that the variable h shifts the function horizontally while the variable k shifts the function vertically.
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
The cube root function is given by:
\(y = \sqrt[3]{x}\)
The translated function is given by:
\(y = \sqrt[3]{x - h} + k\).
The variables work as follows:
Variable h is in the domain, hence it changes the function horizontally.Variable k is in the range, hence it changes the function vertically.More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
Evaluate cos 120° without using a calculator.A.NICOOB. - 1/2O C. 1/2OD. -³

Answers
Explanation
We are required to evaluate cos 120° without using a calculator.
This is achieved thus:
We know that 120° lies in the second quadrant.
We also know that cosine is negative in the second quadrant.
Therefore, we have:
\(\begin{gathered} \cos120\degree=\cos(180\degree-60\degree) \\ \Rightarrow-\cos60\degree \\ \text{ We know that }\cos60\degree=\frac{1}{2} \\ \\ \therefore-\cos60\degree=-\frac{1}{2} \end{gathered}\)Hence, the answer is:
\(-\frac{1}{2}\)Option B is correct.
The value of the trigonometric ratio \(cos 120^0\) without using a calculator is \(\dfrac{-1}{2}\), So the option \(B\) is correct.
The trigonometric ratio \(cos \theta\) is a periodic function and a continuous function that lies from \((-1 \ to +1 )\). In a right-angle triangle, it can be expressed as the ratio of base and hypotenuse.
The trigonometric function \(cos \ 120 ^0\) lies in the second quadrant where all trigonometric functions are negative except \(sin\) function.
It can be calculated as :
\(Cos (180 ^0 - \ \theta ) = Cos \ \theta \\Cos ( 180 ^0 - 120^0) = Cos 60 ^0\\\)
Since \(Cos \theta\) is negative in the second quadrant, so
\(- Cos 60 ^0 = \dfrac {-1}{2}\)
Hence, \(Cos 120^0\) is equal to\(\dfrac{-1}{2}\).
Learn more about trigonometric ratios here:
https://brainly.com/question/29024806
#SPJ6
You are at a coffee shop and notice that as the temperature of the room gets colder, more people order hot beverages. From this observation, you conclude that there is a _______ between the temperature and hot beverage sales at this coffee shop. Group of answer choices negative relationship curvilinear relationship no relationship positive relationship
Answers
Answer:
negative relationship.
Step-by-step explanation:
An experiment can be defined as an investigation which typically involves the process of manipulating an independent variable (the cause) in order to be able to determine or measure the dependent variable (the effect).
This ultimately implies that, an experiment can be used by scientists to show or demonstrate how a condition causes or gives rise to another i.e cause and effect, influence, behavior, etc in a sample.
Cause and effect can be defined as the relationship between two things or events in which an occurrence one (cause) leads to the occurrence of another (effect).
A negative relationship or correlation can be defined as the relationship between two variables in which there exist an inverse relationship between them i.e as one variable increases, the other decreases and vice-versa.
In this scenario, you are at a coffee shop and notice that as the temperature of the room gets colder, more people order hot beverages. From this observation, you conclude that there is a negative relationship between the temperature and hot beverage sales at this coffee shop because for the temperature to get colder it would decrease and for the hot beverages to be hot, its temperature must be increased.
In a group of 1,100 youths, each uses smart phones, either I-phone or Samsung or both or neither, 150 of them use only I-phone, 770 of them use Samsung and 900 use only one of these two smart phones. (1) Find the number of youths who use both of these smart phones. (ii) Find the number of youths who use neither of these smart phones.
Answers
The requried, 20 youths use both iPhone and Samsung, and 200 youths use neither iPhone nor Samsung.
Let A be the set of youths using only iPhones, B be the set of youths using only Samsung, and C be the set of youths using both. Then, we have:
|A| = 150
|B| = 770
|A ∪ B| = 900
We want to find |C| and |A ∩ B| (which is the number of youths using both).
Using the inclusion-exclusion principle, we have:
|A ∪ B| = |A| + |B| - |A ∩ B|
900 = 150 + 770 - |A ∩ B|
|A ∩ B| = 20
So, 20 youths use both iPhone and Samsung.
To find the number of youths who use neither, we can use the fact that:
|A ∪ B ∪ C| = 1100
|A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|
Plugging in the values we know, we get:
1100 = 150 + 770 + |C| - 20 - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|
|C| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C| = 200
Since the number of youths using both is 20, we have:
|A ∩ C| = |B ∩ C| = |A ∩ B ∩ C| = 0
So, we can simplify the equation to:
|C| = 200
Therefore, 200 youths use neither iPhone nor Samsung.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ1
Given the individual rates of workers, to find the combined rate of all the individuals working together you must
the individual rates.
Fill in the blank

Answers
To find the combined rate of all the individuals working together, you must add the individual rates.
How to calculate combined rate of individuals working together?When calculating the combined rate of individuals working together, you need to add up the individual rates. Each worker contributes their own rate of work or productivity, and by adding these rates together, you can determine the combined rate at which they are working collectively.
This allows you to assess the overall efficiency and output of the team or group. By summing up the individual rates, we have better understanding of the overall productivity and performance of the group.
Read more about individual rates
brainly.com/question/31251379
#SPJ1
Determine which conic section is represented based on the given equation: 4x^2+9xy+4y^2-36y-125=0
Answers
The conic section of the equation 4x² + 9x +4y² - 36y - 125 = 0 is a circle
Selecting the conic section of the equationThe given equation is
4x² + 9xy + 4y² - 36y - 125 =0
The above equation is an illustration of a circle equation
The standard form of a circle equation is
(x - a)² + (y - b)² = r²
Where
(a, b) is the center
r is the radius
While the general form of the equation is
ax² + fx + by² + gy + c =0
Where c is a constant
Recall that, we have
4x² + 9x + 4y² - 36y - 125 =0
This is the general form
We can convert to the standard form as follows
Divide through by 4
x² + 2.25x + y² - 9y - 31.25 =0
Next, we complete the square of the x-terms and the y-terms
For the x-terms, we have
x² + 2.25x = x² + 2.25x + (2.25/2)² - (2.25/2)²
x² + 2.25x = (x + 2.25/2)² - (2.25/2)²
For the y-terms, we have
y² - 9y = y² - 9y + (9/2)² - (9/2)²
y² - 9y = (y - 9/2)² - (9/2)²
Substitute the new x and y terms
So, x² + 2.25x + y² - 9y - 31.25 = 0 becomes
(x + 2.25/2)² - (2.25/2)² + (y - 9/2)² - (9/2)²- 31.25 =0
Evaluate the sum of like terms
(x + 2.25/2)² + (y - 9/2)² - 3377/64 = 0
So, we have
(x + 9/8)² + (y - 9/2)² = 3377/64
Using the above as a guide, we can conclude that the conic section of the equation is a circle
Read more about conic section at
brainly.com/question/9702250
#SPJ1
Suppose f left parenthesis x right parenthesis equals 1 minus x squared and g left parenthesis x right parenthesis equals 2 x plus 5. Find the value of f(g(-1).
Answers
Answer:
f(g(-1)) = -8
Step-by-step explanation:
⭐ The two equations we are given are:
\(f(x) = 1-x^2\)\(g(x) = 2x + 5\)This problem is an example of composite functions.
⭐What are composite functions?
Composite functions are functions inside of a functionYou compute the value of an x-value for one function, and use that value for another function.First, we have to compute the value for the 2nd function you see. The 2nd function is inside f(x), and it is g(-1).
Essentially, we have to find the corresponding y-value for when x = -1 in g(x)
\(g(-1) = 2(-1) + 5\)
\(g(-1) = 3\)
Next, take this value and substitute it as the x-value for f(x).
\(f(3) = 1-x^2\)
Now we have to find the y-value for f(x) for when x = 3.
\(f(3) = 1 -3^2\)
⚠️⚠️⚠️!!! CAUTION !!! ⚠️⚠️⚠️
Some people may make the mistake of computing f(3) like this:
\(f(3) = 1 - 3^2\)
\(f(3) = 1+9\\f(3) = 10\)
This is wrong because only 3 is being squared, not -3. Make sure to read the equations you are given carefully to avoid mistakes like this.
\(f(3) = 1-3^2\\f(3) = 1-9\\f(3) = -8\)
∴ f(g(-1)) = -8
Help please!! I’ll give brainliest if you show work as well. Thank you!!!

Answers
Answer:
TWO CRACKERS
Step-by-step explanation:
I'm assuming they want to find x. Here we see that these two are similar triangles, so the sides are reflective. 5x/5 should be equal to 4/x, so 5x/5 = 4/x. If we use cross multiplying we get 5x^2 = 20. divide both sides by 5 and we get x^2 = 4 or x = 2.
Hope this helped
For a floral arrangement class, Jayvon has to create an arrangement of twigs and flowers that has a total of 9 objects. Jayvon has to pay for the twigs and flowers that he uses in his arrangement. Each twig costs $1, and each flower costs $3. He spends a total of $15 on the twigs and flowers. Write and solve a linear system to find the number of twigs and the number of flowers he used. Use the method of substitution.
Answers
Answer:
3 flowers 6 twigs
Step-by-step explanation:
set flowers to x and twigs to y
15 = 3x + y subtract 3x both sides to get y
9 = x+y sub 15-3x in for y 9= x + 15-3x simplify to 2x =6 so x =3 put that in for x in 9=x+y 9= 3+ y so y =6
Select the correct answer. Consider this function. Which graph represents the inverse of function f? f(x)= x+4
Answers
The inverse of the function f(x) = x + 4 is given as f⁻¹(x) = x - 4
What is inverse of a function?An inverse function or an anti function is defined as a function, which can reverse into another function. In simple words, if any function “f” takes x to y then, the inverse of “f” will take y to x. If the function is denoted by ‘f’ or ‘F’, then the inverse function is denoted by f-1 or F-1.
In this problem, the function given is f(x) = x + 4;
We can find the inverse of the function as;
y = x + 4;
Let's switch the variables by replacing x as y and y as x;
x = y + 4
Solving for y;
y = x - 4
f⁻¹(x) = x - 4
The graph of the function is attached below
Learn more on inverse of a function here;
https://brainly.com/question/14391067
#SPJ1

Point A is located at (1, 2). Point B is located at (4, 6). Use this information to determine the length of the line, rounded to the nearest whole number.
Answers
If Point A is located at (1, 2) and Point B is located at (4, 6), the length of the line between points A and B is 5 units.
To determine the length of the line between points A and B, we can use the distance formula, which is a formula used to calculate the distance between two points in a coordinate plane. The distance formula is:
d = √((x₂ - x₁)² + (y₂ - y₁)²)
where (x₁, y₁) and (x₂, y₂) are the coordinates of the two points and d is the distance between them.
Using the coordinates of points A and B, we can substitute their values into the distance formula to find the length of the line between them:
d = √((4 - 1)² + (6 - 2)²)
d = √(3² + 4²)
d = √(9 + 16)
d = √25
d = 5
Rounded to the nearest whole number, the length of the line is also 5 units.
In conclusion, we can use the distance formula to find the length of the line between two points in a coordinate plane. The distance formula uses the coordinates of the two points to calculate the distance between them. The resulting distance can be rounded to the nearest whole number, if needed.
To learn more about distance click on,
https://brainly.com/question/28658621
#SPJ1
Help me please it’s for math class

Answers
Answer:
No solution
Step-by-step explanation:
To start, a solution requires the lines to intersect
However both lines share a slope of -3 and are thus parallel
Since parallel lines dont intersect, there is no solution
Answer:
Hi! The answer to your question is A. No solution, i also have a picture to help you if u need it.
Step-by-step explanation:
☆*: .。..。.:*☆☆*: .。..。.:*☆☆*: .。..。.:*☆☆*: .。..。.:*☆
☆Brainliest is greatly appreciated!☆
Hope this helps!!
- Brooklynn Deka

Help find the slope??

Answers
Answer:
The slope is -1
Answer: -1
Step-by-step explanation:
slope = Δy / Δx = (-3-(-2)) / (3-2) = -1/1 = -1
Negative slope means line goes down
the 2 points to use are (2, -2) and (3, -3)
Given the function:
What is the inverse function of g(x)?
g(x) = -
O g-4(X) = - 2x - 3
Og +(x) = -3(x-3)
O g 7(x)=-3x-2
O g-(x) = -2(x – 3)
Answers
Answer: The answer is D
g-1(x)= -2(x-3)
Step-by-step explanation:
The inverse of a function is its opposite
The inverse of the function g(x) is \(g^{-1}(x)= -2(x-3)\)
The function is given as;
\(g(x) = -0.5x + 3\)
Rewrite as:
\(y = -0.5x + 3\)
Swap the x and y variables
\(x = -0.5y + 3\)
Subtract 3 from both sides
\(-0.5y = x -3\)
Multiply both sides by -2
\(y= -2(x-3)\)
Rewrite as:
\(g^{-1}(x)= -2(x-3)\)
Hence, the inverse of the function g(x) is \(g^{-1}(x)= -2(x-3)\)
Read more about inverse functions at:
https://brainly.com/question/14391067
Loans Bill took out two loans that totaled $15,000. One
of the loans charges 12% per year, and the other charges
10% per year. If the total interest charged in the first year
is $1,600, how much was each loan?
Answers
Let, money in loan with 12% interest is x.
So, money in loan with 10% interest is 15000-x.
Now , sum of interest :
\(\dfrac{12x}{100}+\dfrac{10(15000-x)}{100}=1600\\\\12x+150000-10x=160000\\\\2x=10000\\\\x=5000\)
Therefore, money on 12% interest is $5000 and 10% interest is $10000.
Hence, this is the required solution.
write in two equivalent forms: fraction, decimal, or percent.
7/8
PLEASE ANSWER QUICK!!!!!!!!! I NEED HELP!!!! FAST!!!!
ty
Answers
Answer:
7/8 = 0.875 = 87.5%
Step-by-step explanation:
7/8 = 0.875 = 87.5%
HELP PLEASE YOU'LL GET BRAINLIEST :)
Question: Jack wants to buy a new skateboard.The store is offering a discount of 10%. he also has a store coupon that will give Him a additional 15% off the discounted price.The original price of the skateboard is $45.What is the price of the skateboard after the discount and Jack's coupon.
Answers
45 x 10/100 = 4.5
subtract that from the original price to find the discount:
45 - 4.5 = 40.5
find 15% of 40.5:
40.5 x .15 = 6.075
subtract the discount:
40.5 - 6.075 = 34.425
$34.425 is the discounted price
Which three lengths could be the lengths of the sides of a triangle?
Answers
Any three lengths that satisfy the triangle inequality theorem can form the sides of a triangle. The theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
In order for three lengths to form a triangle, they must satisfy the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Let's consider three lengths: a, b, and c.
To determine if they can form a triangle, we need to check the following conditions:
a + b > c
a + c > b
b + c > a
If all three conditions are true, then the lengths a, b, and c can form a triangle.
For example, let's consider the lengths 3, 4, and 5.
3 + 4 > 5 (True)
3 + 5 > 4 (True)
4 + 5 > 3 (True)
Since all three conditions are true, the lengths 3, 4, and 5 can form a triangle.
Therefore, any three lengths that satisfy the triangle inequality theorem can be the lengths of the sides of a triangle.
For more such question on triangle inequality theorem
https://brainly.com/question/1163433
#SPJ8
What is the range of f(x) = 3* + 9?
O {yly<9}
O {yly>9}
O {yly> 3}
O {yly<3}
Answers
On solving the provided question, we can say that - the range \(|x + 1| = 0\) \(x + 1 = 0 = > x = -1\) and \(y = 3\)
What is range?Finding the variable's greatest observed value (maximum) and deducting the least observed value will yield the range (minimum). Limits of variation or potential range: a variety of steel costs; several styles; The size or scope of an action or operation: insight. how far a weapon's projectile can or will travel. The number in a list or set between the lowest and maximum is referred to as a range. Line up all the numbers before locating the region. After that, take away (get rid of) the lowest number from the greatest number. The solution provides the list's range.
The regions where the absolute values are zero are known as the vertex points of an absolute value function.
\(|x + 1| = 0\\x + 1 = 0\\x = -1\)
\(y = |-1 + 1| + 3\\y= 0 + 3\\y = 3\)
To know more about range visit:
https://brainly.com/question/28135761
#SPJ1
What is this! I will mark u as branilyst

Answers
because the triangle angles must measure to 180 and the scalene triangle states that the base angles add up to 86. Subtract 86 from 100, you get 94. Angle two is 94. 94-100=x
I need help with this
look at picture
Complementary angles

Answers
18°
Mark as brainlist......
Answer:
18 degrees.
Step-by-step explanation:
....you welcome
HELP HURRY! YOU GET 50 POINTS AND ILL MARK YOU BRAINLY!!
A right rectangular prism is packed with cubes of side length fraction 1 over 5 inch. If the prism is packed with 15 cubes along the length, 6 cubes along the width, and 5 cubes along the height, what is the volume of the prism?
fraction 2 and 3 over 10 cubic inches
fraction 3 and 3 over 5 cubic inches
fraction 7 and 1 over 5 cubic inches
fraction 7 and 1 over 10 cubic inches
Answers
Answer:
3.6 in³
This should be the correct answer, good luck!
2x-7= -5x+14
with explanation pls.
Answers
First, add 7 to both sides of the equation so it would be;
2−7=−5+14
2−7 + 7=−5+14+7
To simplify this it would be:
2=−5+21
Add 5 to both sides, it would look like this:
2=−5+212+5=−5+21+5
To simplify it would be;
7=21
Divide both sides of equation with once again, the same number
7=21 77=217
Simplify it;
=3
Therefore your answer is;
=3
6x = 52 − 2y 5x + 7y = 70 Question 1 What is the first step when solving the given system by the elimination method?
Answers
The solution of the equations 6x = 52 − 2y and 5x + 7y = 70 by elimination method will be (7, 5).
What is the solution to the equation?In other words, the collection of all feasible values for the parameters that satisfy the specified mathematical equation is the convenient storage of the bunch of equations.
The equations are given below.
6x = 52 - 2y
6x + 2y = 52
3x + y = 26 ...1
5x + 7y = 70
(5/7)x + y = 10 ...2
Subtraction equation 2 from equation 1, then we have
3x - (5/7)x = 26 - 10
(16/7)x = 16
x = 7
Then the value of 'y' is given as,
3(7) + y = 26
21 + y = 26
y = 5
The solution of the equations 6x = 52 − 2y and 5x + 7y = 70 by elimination method will be (7, 5).
More about the solution of the equation link is given below.
https://brainly.com/question/22613204
#SPJ1
Write the equation
Show how to solve

Answers
(Giving brainliest! Pls have at least one sentence to explain why you chose the answer :) )
Rodney sold 45,612 copies of his book and Beth sold 45,612 x one half copies of her book. Which statement compares the numbers of book copies sold?
A) Beth sold half the number of book copies that Rodney sold.
B) Rodney sold half the number of book copies that Beth sold.
C) Beth sold twice the number of book copies that Rodney sold.
D) Rodney sold the same number of book copies that Beth sold.
Answers
Answer:
A
Step-by-step explanation:
Hope it helps
Answer:The awnser is
B
Step-by-step explanation:
because rodney sold half her copies
Given this transformation, find the period and any asymptotes in order to sketch it
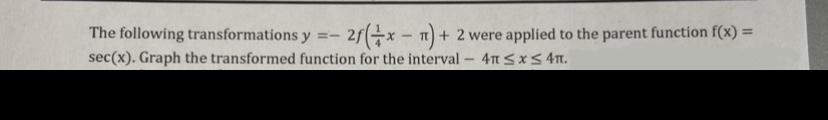
Answers
In this problem, we have the parent function f(x) = sec(x).
This function is transformed in the following way:
\(f(x)\rightarrow g(x)=-2\cdot f(\frac{1}{4}x-\pi)+2.\)(1) Applying this transformation to the parent function f(x), we get:
\(g(x)=-2\cdot sec(\frac{1}{4}x-\pi)+2.\)(2) Plotting this function in the interval -4π ≤ x ≤ 4π, we get the following graph:
Answer
