A small treasure chest is in the shape of a rectangular prism.
The length of the chest is y feet, the width ½ y feet, and the height
2y feet. The chest holds 8 cubic feet of treasure. What are the
dimensions of the treasure chest?
Answers
Answer:
length = 2ft
width = 1 ft
height = 4 ft
Step-by-step explanation:
V = LWH
V = (1/2)y × y × 2y
V = y³ = 8 ft³
y = 2
length = 2ft
width = (1/2)(2 ft) = 1 ft
height = 2(2 ft) = 4 ft
Related Questions
how many bottles can u buy for $3
Answers
Answer:
3?
Step-by-step explanation:
It depends on the price of the bottle, for example if the bottle is $1 then you can buy 3 but if it's 50¢ then you can buy 6. If there is tax then the amount of bottles you buy will be less than what it be without tax
If 5 people arrive at the coffee shop each minute (during rush hour) and they each have to wait 3 minutes to be served; how long is the line on average at the coffee shop during rush hour?
Answers
The line at the coffee shop during rush hour is 15 people long.
Given:
- 5 people arrive at the coffee shop each minute.
- Each person has to wait for 3 minutes to be served.
Since 5 people arrive each minute, the rate of people entering the line is 5 people/minute.
Now, Each person has to wait for 3 minutes to be served.
So, Average length of line = Rate of people entering * Time for a person to be served
Average length of line = 5 people/minute * 3 minutes
Average length of line = 15 people
Therefore, on average, the line at the coffee shop during rush hour is 15 people long.
Learn more about Unitary Method here:
https://brainly.com/question/28276953
#SPJ4
What is the Value of P? 9=p÷9
Answers
Answer:
p = 81
Step-by-step explanation:
9 = \(\frac{p}{9}\) Multiply both sides by 9
9(9) = \(\frac{p}{9}\)\((\frac{9}{1})\) another name for 9 is \(\frac{9}{1}\)
81 = p
8x-9(x-9)=-(9x-16)+9(x-1)
Answers
Answer: X=74
if you want to be shown step by step comment below
a number is doubled and then increased by seven. The result is ninety one. what is the original number?
Answers
Answer:
The anwser to this is 41
Step-by-step explanation:
91 - 7 = 82, 82/2 = 41
The cost of an apple is $1.20. What is the cost of 5 apples?
Answers
Answer:
0.24
Step-by-step explanation:
$1.20 ÷ 5 = 0.24
To check that we are going to multiply \(5 x 0.24 = $1.20\\\)
I hope this helps and have a great day!
the square root of 72 is it closer to 8 or 9
Answers
ming Math th grade > Assessment Language arts Analytics S.11 Solve two-step equations: word problems D2Y Science 18c+ 4 = 42 4c+18 42 Painted Pots lets customers choose and paint their own pottery. The store has teap multiple sizes. Rebecca chose to paint the largest teapot offered, which cost $18. She a painted 4 small teacups to go with her teapot. Rebecca spent a total of $42 on pottery. Which equation can you use to find c, the cost of each teacup? Learn with an example ✓ OF Watch a video > Social studies 4(c + 18) 42 = Recommendations 18(c + 4) = 42
Answers
The equation representing the cost of each teacup is given as follows:
4c + 18 = 42.
Hence the cost is of: $6.
How to define a linear function?The slope-intercept representation of a linear function is given by the equation presented as follows:
y = mx + b
The coefficients of the function and their meaning are described as follows:
m is the slope of the function, representing the rate of change.b is the y-intercept of the function, which is the initial value.The meaning of the slope and of the intercept for this problem are given as follows:
Slope -> cost per teacup.Intercept: fixed cost.Hence the function is given as follows:
C = xc + 18.
(as the cost of the pot is of $18).
4 teacups push the price up to $42, hence the equation is given as follows:
4c + 18 = 42
4c = 24
c = 6.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
TIME REMAINING
43:25
Triangles X Y Z and X prime Y prime Z prime are shown.
ΔXYZ was reflected over a vertical line, then dilated by a scale factor of One-half, resulting in ΔX'Y'Z'. Which must be true of the two triangles? Select three options.
△XYZ ~ △X'Y'Z'
AngleXZY ≅ AngleY'Z'X'
YX ≅ Y'X'
XZ = 2X'Z'
mAngleYXZ = 2mAngleY'X'Z'
Answers
Answer:
△XYZ ~ △X'Y'Z'AngleXZY ≅ AngleY'Z'X'XZ = 2X'Z'Step-by-step explanation:
Reflection over any line is a rigid transformation that does not change angles or lengths. Dilation is a transformation that changes lengths by the same scale factor, but has no effect on angles. Dilated figures are similar to the original.
ApplicationWhen ΔXYZ is reflected over a vertical line, no lengths or angles are changed. When the reflected triangle is dilated by half, we get ...
Y'X' = (1/2)YX . . . . . . . makes option 3 false
X'Z' = (1/2)XZ . . . . . . . makes option 4 true
Since no angles are changed, we have ...
Angle XZY ≅ Angle Y'Z'X' (another name for angle X'Z'Y')
... makes option 2 true
Of course, the resulting triangle is similar to the original, so ...
△XYZ ~ △X'Y'Z' . . . . . option 1 is true
3. Calculate the following: a) 5-9 d) 8-8 g) -1 + 12 j) -12 + 12 m) -2 +4+3 p) -4-3+2-1 4. Calculate the following: a) 3+ -2 d) −5+-2 al 2−−3+-4 mo b) 2 + 7 e) −2+5 h)-8-22 k) 2+4-3 n) -2+4-3 193 b)-4--56/t e) 8-+3 h) | +-2--3
Answers
The arithmetic expressions are solved and answered below -
5 - 9 = - 4
8 - 8 = 0
- 1 + 12 = 11
- 12 + 12 = 0
- 2 + 4 + 3 = 5
- 4 + 3 + 2 - 1 = - 2 + 2 = 0
What are algebraic expressions?In mathematics, an expression or mathematical expression is a combination of terms both variables and constants. For example -
2x + 4y + 5z
4y + 2x
Given are the expressions as given in the questions.
{a} -
5 - 9 = - 4
{b} -
8 - 8 = 0
{c} -
- 1 + 12 = 11
{d} -
- 12 + 12 = 0
{e} -
- 2 + 4 + 3
5
{f} -
- 4 + 3 + 2 - 1 = - 2 + 2 = 0
Therefore, the arithmetic expressions are solved and answered below -
5 - 9 = - 4
8 - 8 = 0
- 1 + 12 = 11
- 12 + 12 = 0
- 2 + 4 + 3 = 5
- 4 + 3 + 2 - 1 = - 2 + 2 = 0
To solve more questions on arithmetic operations, visit the link below
https://brainly.com/question/20562711
#SPJ9
{Complete question -
Calculate the following:
a) 5-9
b) 8-8
c) -1 + 12
d) -12 + 12
e) -2 +4+3
f) -4-3+2-1}
for a positive integer nn and nonzero digits aa, bb, and cc, let a na n be the nn-digit integer each of whose digits is equal to aa? let b nb n be the nn-digit integer each of whose digits is equal to bb, and let c nc n be the 2n2n-digit (not nn-digit) integer each of whose digits is equal to cc. what is the greatest possible value of a b ca b c for which there are at least two values of nn such that c n - b n
Answers
The greatest possible value of a b ca b c occurs when aa, bb, and cc are the largest possible digits.
This value can be calculated by subtracting the two largest values of b n b_n from c n c_n for different values of nn and finding the maximum result.
Let's consider the largest possible digits for aa, bb, and cc. Since aa, bb, and cc are nonzero digits, the largest possible digit is 9.
To find the greatest possible value of a b ca b c, we need to find the maximum difference between c n c_n and b n b_n for different values of nn. Since a na n has nn digits with all digits equal to aa, the maximum value of a na n is nn times aa.
For b nb n , we have nn digits with all digits equal to bb, so the maximum value of b nb n is nn times bb.
Lastly, for c nc n , we have 2n digits with all digits equal to cc. The maximum value of c nc n is 2n times cc.
To find the maximum difference between c n c_n and b n b_n, we subtract b nb n from c nc n :
c n - b n = (2n * cc) - (nn * bb)
We can calculate this difference for different values of nn and find the maximum result. The largest possible value of a b ca b c occurs when this difference is maximum.
Please note that specific values of nn, aa, bb, and cc are not provided, so we cannot calculate the exact value. However, the approach described above can be used to find the greatest possible value based on the given conditions.
Learn more about subtracting here:
brainly.com/question/13619104
#SPJ11
HOW DO I SOLVE THIS 20POINTS

Answers
The solution of the system of equations f(x) = 2^x + 1 and g(x) = 3^x is x = 1
Determining the solution of the system of equationsFrom the question, we have the following parameters that can be used in our computation:
f(x) = 2^x + 1
g(x) = 3^x
The above expression is a system of exponential equations
We are required to solve by graph
That implies that we graph the equations in the system on the same plane and write out ordered pairs from the point of intersection of the equations in the system
Next, we plot the graph
See attachment for the graph of the equations
The ordered pairs of the intersection point is (1, 3)
Read more about equations at
https://brainly.com/question/148035
#SPJ1

To calculate the interquartile range, Daniel subtracts the highest and lowest number within a given dataset. Is this method correct?
Answers
Daniel's method is incorrect, as the interquartile range is given by the difference between the third quartile and the first quartile.
What is the interquartile range of a data-set?The interquartile range of a data-set is by the difference of the 75th percentile(Q3) by the 25th percentile(Q1) of the data-set.
The quartiles are described as follows:
Q3: Median of the upper half of the data-set.Q1: Median of the lower half of the data-set.From this, we get that the quartiles are related to the median of the set, that is, neither is given by the highest and by the lowest values, hence the interquartile range is given by the difference between the third quartile and the first quartile.
More can be learned about the interquartile range of a data-set at https://brainly.com/question/17083142
#SPJ1
you get $2,000 loan at 9% interest rate and pays it back in 6 months. how much intereast will you pay on the loan
Answers
Answer:
$90
Step-by-step explanation:
First, converting R percent to r a decimal
r = R/100 = 9%/100 = 0.09 per year,
then, solving our equation
I = 2000 × 0.09 × 0.5 = 90
I = $ 90.00
The simple interest accumulated
on a principal of $ 2,000.00
at a rate of 9% per year
for 0.5 years is $ 90.00.
2) find the equations of the straight lines given the slope m and one point. be prepared to show your work on paper to your teacher. m= -2 point (-1,-2) x1= _______ y1=_____ equation: _________________
Answers
The equation of the straight line is y = -2x - 4, the value of x₁ is -1 and the value of y₁ is -2.
To find the equation of a straight line given its slope and one point, we use the point-slope form of the equation:
−y − y₁ = m(x−x₁ )
where m is the slope of the line, and (x₁, y₁) is the given point.
In this case, m = -2 and the point is (-1, -2). So we have:
x₁ = -1
y₁ = -2
m = -2
Substituting these values into the point-slope form, we get:
y−(−2)=−2(x−(−1))
Simplifying and rearranging terms, we get the equation of the line:
y + 2 = -2x - 2
y = -2x - 4
Find out more about straight lines
brainly.com/question/23805201
#SPJ4
can someone plz help me wit dis plz

Answers
Answer:
b = 6.1 ft
Step-by-step explanation:
The area (A) of a triangle is calculated as
A = \(\frac{1}{2}\) bh ( b is the base and h the perpendicular height )
Here A = 10.98 and h = 3.6 , then
\(\frac{1}{2}\) × b × 3.6 = 10.98
1.8b = 10.98 ( divide both sides by 1.8 )
b = 6.1
A ratio of two complementary angles is 3:7 find the measures of both angles
Answers
Given the word problem, we can deduce the following information:
1. The ratio of the two complementary angles is 3:7.
To determine the measures of both angles, we must note first that complementary angles are two angles whose measures add up to 90°. So our equation would be:
\(3x+7x=90\)We simplify the equation above:
\(\begin{gathered} 3x+7x=90 \\ 10x=90 \\ x=\frac{90}{10} \\ x=9 \end{gathered}\)We plug in x=9 into 3x to get the first angle:
Angle 1 = 3x = 3(9) = 27
Then, we plug in x=9 into 7x to get Angle 2:
Angle 2= 7x=7(9)=63
Therefore, the measures of both angles are 27° and 63°.
what is the missing number. Good points

Answers
Answer:
Which number is missing?
40 38 35 31 26 20 13 5
Pattern: ( -2, -3, -4, etc)
40 - 2 = 38
38 - 3 = 35
35 - 4 = 31
31 - 5 = 26
26 - 6 = 20
20 - 7 = 13
13 - 8 = 5
Step-by-step explanation:
You're welcome.
Classify this number as rational, irrational, or nether: 6
Answers
Answer:
The answer is : Rational
8. Alvin purchased $1,300,000 worth of videogame set and made a $150,000 down payment. He agreed to pay the balance by making equal payments at the end of each month for 20 years. What is the size of the monthly payment if the interest charged is 16% compounded quarterly?
Answers
We have a purchase of $1,300,000.
The downpayment is $150,000 and the rest is financed.
We can calculate the amount that is owed as:
\(\begin{gathered} C=1,300,000-150,000 \\ C=1,150,000 \end{gathered}\)This amount will be paid in equal amounts, monthly for 20 years.
The interest rate is 16% compounded quarterly.
We have to start by converting the interest rate in a monthly-compounded equivalent rate.
A rate of 16% compounded quarterly (m=3) will be equivalent to a monthly rate r. We can calculate r as:
\(\begin{gathered} (1+r)^{12}=(1+\frac{0.16}{3})^3 \\ (1+r)^4=1+\frac{0.16}{3} \\ (1+r)^4\approx1+0.05333 \\ 1+r\approx1.0533^{\frac{1}{4}} \\ r\approx1.013-1 \\ r\approx0.013 \end{gathered}\)We then can calculate the payments as an annuity with r = 0.013 and 20*12 = 240 payments.
We can calculate the amount he will pay each month as:
\(\begin{gathered} P=\frac{r\cdot PV}{1-(1+r)^{-n}} \\ P=\frac{0.013\cdot1150000}{1-(1+0.013)^{-240}} \\ P=\frac{14950}{1-1.013^{-240}} \\ P=\frac{14950}{1-0.045} \\ P=\frac{14950}{0.955} \\ P=15654.45 \end{gathered}\)Answer: the monthly payment is approximately $15654.45.
HELP ASAP!!!!!!!!!
I can’t find the slope

Answers
Answer:
The slope of the line is -2.
Step-by-step explanation:
y = mx + b
The "m" variable is the slope.
m = \(\frac{y_{2} - y_{1} }{x_{2} - x_{1}}\)
\(y_{2}\) is the second "y" value given in the table. \(y_{1}\) is the first value given. Same thing for \(x_{2}\) and \(x_{1}\).
m = \(\frac{y_{2} - y_{1} }{x_{2} - x_{1}}\)
m = \(\frac{(-5) - 3}{(-1) - (-5)}\)
m = \(\frac{-8}{4}\)
m = -2
PLEASE ANSWER PLEASEEEEEEEEE

Answers
Answer:
C
Step-by-step explanation:
11 | 2 means 112
A is wrong because 11 | 2 cannot mean 12.
B is wrong because stem with value 1 doesn't exist.
D is wrong because stems and leaves are not added to give real value.
Hope this helps!
consider this polynomial equation
6(x-3)(x^2+4)(x+1)=0
the equation has ( A. 2 B.3 C.4) solutions. it's real solutions are x = (-2 -1 and 2 or. -1 and 3)

Answers
Answer:
2 solutions
-1 and 3 is the real solutions
Question H3 Suppose f(8) = 6 and f'(8) = 4. Find the following. el (z) - e6 lim x24x - 32 ef(x) -6 - f(x) + 5 x² + 16x + 64 18 lim z 8 = 8
Answers
Using L'Hopital's rule `18 lim z->8 (1 + 8/z)^(z/8) = 18e^8`
Given information; f(8) = 6 and f'(8) = 4.
Suppose f(8) = 6 and f'(8) = 4. Find the following. Part A: `el (z) - e6`
We know that; $e^0 = 1$ and $e^x > 0$ for all $x$.
Therefore, `el (z) - e6 = e^0 - e^6 = 1 - e^6`
Part B: `lim x->24x - 32 ef(x) -6 - f(x) + 5 x² + 16x + 64`Let, `y = x - 8`
Then, `x = y + 8` and `f(x) = f(y + 8)`
Now, rewrite the expression in terms of `y`;`lim y->0 ((2y + 8)^2 - 32) (f(y + 8) - 6 - f'(8)y + 5y^2 + 32y + 64)`
Using the given values;`lim y->0 ((2y + 8)^2 - 32) (f(y + 8) - 6 - 4y + 5y^2 + 32y + 64)`
Part C: `18 lim z->8 = 8`
Using L'Hopital's rule;`lim z->8 (1 + 8/z)^(z/8) = e^8`
Therefore, `18 lim z->8 (1 + 8/z)^(z/8) = 18e^8`
More on L'Hopital's rule: https://brainly.com/question/24331899
#SPJ11
Function A is given by the equation y = 3 x + 10 . Function is given by the example show. When x = 1, y =10. When x = 2, y = 13. When x = 3, y = 16. When x = 4, y = 19.
Function A has a..
A. Greater rate of change
B. Smaller rate of change
C. Greater y-intercept
D. Smaller y- intercept
Answers
Answer: both of you have a lead yet but you can get it right away if I can see you guys again in a developer way but I have a game pass
Step-by-step explanation: yes
The following series are geometric series or a sum of two geometric series. Determine whether each series converges or not. For the series which converge, enter the sum of the series. For the series which diverges enter "DIV" (without quotes). (a) ∑n=1[infinity]8n7n= , (b) ∑n=2[infinity]13n= , (c) ∑n=0[infinity]3n92n+1= , (d) ∑n=5[infinity]7n8n= , (e) ∑n=1[infinity]7n7n+4= , (f) ∑n=1[infinity]7n+3n8n=
Answers
(a) ∑n=1[infinity]8n7n is a geometric series and it diverges. Answer: DIV.
(b) ∑n=2[infinity]13n is a geometric series and it diverges. Answer: DIV.
(c) ∑n=0[infinity]3n92n+1 is a geometric series and it converges. Sum = 2.452.
(d) ∑n=5[infinity]7n8n is a geometric series and it converges. Sum = 0.0954.
(e) ∑n=1[infinity]7n7n+4 is a geometric series and it converges. Sum = 3.5
(f) ∑n=1[infinity] 7/8*\((7/8)^{(n-1)\) + \(3/8*(3/8)^{(n-1)\). Both of these are geometric series and the series converges. Sum= 1.6.
(a) This series can be rewritten as ∑n=1[infinity]\((8/7)^n\). This is a geometric series with ratio r=8/7 which is greater than 1. Hence, the series diverges. Answer: DIV.
(b) This is a geometric series with first term a=13 and common ratio r=13. Since |r|>1, the series diverges. Answer: DIV.
(c) This series can be written as ∑n=0[infinity] \(3^n/(9^2)^n\) * \(9^{(1/(2n+1))\). The first part of the series is a geometric series with a=1 and r=3/81<1. The second part of the series is also a geometric series with a=\(9^{(1/3)\) and r=\((9^{(1/3)})^2=9^{(2/3)\)<1. Therefore, the series converges. To find the sum, we use the formula for the sum of an infinite geometric series:
sum = a/(1-r) + b/(1-c)
where a and r are the first term and common ratio of the first geometric series, and b and c are the first term and common ratio of the second geometric series. Substituting the values, we get:
sum = 1/(1-3/81) + \(9^{(1/3)}/(1-9^{(2/3))\)
= 1.01 + 1.442
= 2.452
Answer: 2.452.
(d) This series can be written as ∑n=5[infinity] \((7/8)^n\). This is a geometric series with ratio r=7/8 which is less than 1. Hence, the series converges. To find the sum, we use the formula for the sum of an infinite geometric series:
sum = a/(1-r)
where a and r are the first term and common ratio of the series. Substituting the values, we get:
sum = \((7/8)^5/(1-7/8)\)
= \(7/8^4\)
= 0.0954
Answer: 0.0954.
(e) This series can be rewritten as ∑n=1[infinity] \((7/7.4)^n\). This is a geometric series with ratio r=7/7.4<1. Hence, the series converges. To find the sum, we use the formula for the sum of an infinite geometric series:
sum = a/(1-r)
where a and r are the first term and common ratio of the series. Substituting the values, we get:
sum = 1/(1-7/7.4)
= 3.5
Answer: 3.5.
(f) This series can be rewritten as ∑n=1[infinity] \(7/8*(7/8)^{(n-1)\) + \(3/8*(3/8)^{(n-1)\). Both of these are geometric series with ratios less than 1, so the series converges. To find the sum, we add the sums of the two geometric series:
sum = 7/8/(1-7/8) + 3/8/(1-3/8)
= 1 + 3/5
= 1.6
Answer: 1.6.
For more such questions on Geometric series.
https://brainly.com/question/4617980#
#SPJ11
At a sale this week, a sofa is being sold for $416. This is a 35% discount from the original price.
What is the original price?
Х
?
Answers
65% is $416
65% = $416
1% = $6.40
100% = $6.40 x 100 = $640
So the original price of a sofa is $640
In circle R with m/QRS = 30 and QR = 4 units, find the length of arc QS.
Round to the nearest hundredth.
R
S
Q
Answers
The length of arc QS is approximately 2.09 units.
The length of an arc of a circle:
Length of arc = (central angle / 360) × 2 × π × radius
Central angle is the angle in degrees formed by the two radii that define the arc and radius is the radius of the circle.
In this case, we are given that m∠QRS = 30 means that the central angle formed by radii QS and QR is 30 degrees.
We are also given that QR = 4 unit
The radius of the circle is also 4 units.
Substituting these values into the formula, we get:
Length of arc QS = (30 / 360) × 2 × π × 4
Simplifying and rounding to the nearest hundredth we get:
Length of arc QS ≈ 2.09
The length of arc QS is approximately 2.09 units.
An arc of a circle's length:
Arc length equals (central angle / 360) divided by 2 and radius.
Radius is the diameter of the circle, while central angle is the angle, in degrees, produced by the two radii that constitute the arc.
In this instance, we are told that mQRS = 30 denotes the centre angle of 30 degrees created by radii QS and QR.
Also stated is that QR equals 4 units.
The circle also has a radius of 4 units.
When these values are added to the formula, we obtain:
Arc length QS = (30 / 360) 2 4
Rounding to the closest hundredth and simplifying, we obtain:
Arc length QS = 2.09
Arc QS has a length of around 2.09 units.
For similar questions on length
https://brainly.com/question/28322552
#SPJ11
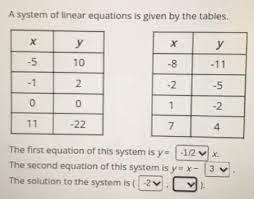
Select the correct answer from each drop-down menu. A system of linear equations is given by the tables. x y -5 10 -1 2 0 0 11 -22 x y -8 -11 -2 -5 1 -2 7 4 The first equation of this system is y = x. The second equation of this system is y = x − . The solution to the system is ( , ).
Answers
For the linear equations provided by the coordinates in the table;
The first equation of this system is y = -2x.
The second equation of this system is y = x - 3.
The solution to the system is (1, -2).
How do we solve for the system of linear equation?We have four points (-5,10), (-1,2), (0,0), and (11,-22) for first equation, and four points (-8,-11), (-2,-5), (1,-2), and (7,4) the second equation.
The slope (m) is given by the formula (y2 - y1) / (x2 - x1).
For the first line, we can use the points (-5,10) and (-1,2)
m1 = (2 - 10) / (-1 - (-5)) = -8/4 = -2.
the first equation is y = -2x
the second line, we can use the points (-8,-11) and (-2,-5)
m2 = (-5 - -11) / (-2 - -8) = 6/6 = 1.
the second line has a slope of 1,
the equation should have the form y = x + c.
To find c, we can use one of the points, for instance (-2,-5):
-5 = -2 + c => c = -5 + 2 = -3.
So, the second equation is y = x - 3.
the solution to the system, we need to find where the two lines intersect.
y = -2x
y = x - 3
Setting both equation equally
-2x = x - 3
=> 3x = 3
=> x = 1.
Substituting x = 1 into the first equation
y = -2(1) = -2.
the solution to the system of linear equation would be (1, -2).
Find more exercises on linear equation;
https://brainly.com/question/29739212
#SPJ1
for a repeated measures anova, given n = 78 k = 7 ssb = 8 ssw = 8 sserror = 71 what is the value of the mean squares error term (mserror)?
Answers
For a repeated measures ANOVA for n = 78, k = 7, SSb = 8, SSw = 8, SSerror = 71 , the value of Mean Square Error Term is 1 .
The Mean Squares Error Term (MSerror) is calculated by dividing the sum of squares error (SSerror) by the degrees of freedom for error (dfe), which is equal to (n - k). So , we have:
⇒ MSerror = (SSerror)/(dfe) ,
For n = 78 and k = 7 ,
We get ,
The degree of freedom for error (dfe) = 78 - 7 = 71 ,
So , MSerror = (SSerror)/(dfe) ,
⇒ MSerror = 71/(78 - 7) ,
⇒ MSerror = 71/71 ,
⇒ MSerror = 1
Therefore, the value of MSerror is equal to 1.
Learn more about ANOVA here
https://brainly.com/question/28206398
#SPJ4
The given question is incomplete , the complete question is
For a repeated measures ANOVA, given n = 78, k = 7, SSb = 8, SSw = 8, SSerror = 71 . What is the value of the mean squares error term (MSerror)?