A sports store has 116 soccer balls. over 6 months, it sells 8 soccer balls per month. how many soccer balls are in an inventory at the end of the 6 months?

The solution of the system of equations is x = 10 and y = 20.  

A quadratic equation is a second-order polynomial equation in one variable x ax2 + bx c=0. with  ≠ 0. Since this is a quadratic polynomial equation, the Fundamental Theorem of Algebra ensures that it has at least one solution. The solution can be real or complex

To solve an equation, you must find the value of x that makes both equations true at the same time. Once you find the value of x, you can substitute it  into both equations to find the corresponding value of y.  

One way to do this is to set the two expressions for y equal to each other, since  both are equal to y:

2x = 3x - 10

Subtracting 2x from both sides, we get:

-x = -10

Dividing both sides by -1 gives:

x = 10

Now that we know that x = 10, we can substitute it into both equations to find the corresponding value of y. Let's use the first equation:

y = 2x = 2(10) = 20

Therefore, the solution of the system of equations is x = 10 and y = 20.

Learn more about polynomial equation here

https://brainly.com/question/30127172

#SPJ1

A) the car rate (R) of gas consumption in miles per gallon will be the miles he grive divided by the gallons he spend so first we have to find the number of miles he drive so:

So the rate will be:

B) the average cost in dollars per day will be the total amount of money divided by the number of days he use the car so we know he uses the car for 3 days so the average will be:

And the averarage rate of travel in miles per days will be:

The range of the function y = 4x + 1 is {y | 1 ≤ y ≤ 41}.

What is the range of data?

The range of data is defined as a measure of the difference between the maximum value of data and the minimum value of data.

The function is given as y = 4x + 1.

The range of the function y = 4x + 1 is the set of all possible output values that the function can produce.

Given that the domain of the function is 0 ≤ x ≤ 10.

The range of this function is the set of all y-values that can be obtained by plugging in x-values between 0 and 10 into the function.

Plugging in x = 0, the value for y = 4(0) + 1 = 1.

Plugging in x = 10, the value for y = 4(10) + 1 = 41.

The range of the function y = 4x + 1 is the set of all y-values between 1 and 41, inclusive.

Therefore, the range of the function is {y | 1 ≤ y ≤ 41}.

To learn more about range of data from the given link

https://brainly.com/question/20607770

#SPJ1

Cluster analysis is a valuable tool in data analysis that helps identify hidden patterns and group similar objects or data points.

It is useful in various fields, such as market research, image analysis, customer segmentation, and anomaly detection. By clustering data, we can gain insights, make predictions, and improve decision-making. Hierarchical clustering is a specific approach to cluster analysis. It organizes data points into a hierarchy of clusters, where each cluster can contain subclusters. This method allows for a hierarchical structure that captures different levels of similarity or dissimilarity between data points.

For example, in customer segmentation, hierarchical clustering can group customers based on similar attributes like demographics, purchase history, and behavior. In image analysis, it can be used to segment images into meaningful regions or objects based on their visual characteristics. Hierarchical clustering offers a flexible and interpretable way to analyze complex datasets and discover underlying structures.

To learn more about data points click here: brainly.com/question/17148634

#SPJ11

Answer:

Finding the y value is easy if you know the slope of the line and the x coordinate. Review the equation for the slope of a line. The equation for finding the slope is: m = [y1 - y2] / [x1 - x2]. If you know x, you can solve for y to find the y value for the slope of the line.

Step-by-step explanation:

Answer:

b)

Step-by-step explanation:

Surface area of a cube = 6a²   , here a is the side of cube

When side is halved, side = a/2

Now, the surface area of new cube = 6* (a/2)²

                                                           = \(6*\frac{a^{2}}{4}=\frac{1}{4}*6a^{2}\\\)

                                                            = one fourth of the cube

A box contains five cards lettered A,A,B,C,D. If one card is selected at random from the box and NOT replaced, what is the probability that Jill will draw an A and then a C?​

step 1

Find the probability that Jill draw an A

P=2/5

step 2

Find the probability that jill draw a C

P=1/4

therefore

the probability that Jill will draw an A and then a C is

P=(2/5)(1/4)

P=2/20

The equation for the amount of money in the account after t years in continuous compounding is A(t) = 700e^(0.05t). We find that the amount of money in the account after 5 years is approximately $866.85. The equation for the amount of money in the account after t years in monthly compounding is A(t) = 700(1 + 0.05/12)^(12t)

In part 1, the equation for the amount of money in the account after t years in continuous compounding is A(t) = 700e^(0.05t). The graph of this equation represents the growth of the account balance over time. In part 2, using the graph, we find that the amount of money in the account after 5 years is approximately $866.85.

In part 3, the equation for the amount of money in the account after t years in monthly compounding is A(t) = 700(1 + 0.05/12)^(12t). The graph of this equation is plotted on the same graph as part 1, showing the growth of the account balance with monthly compounding. In part 4, using the graph, we find that the amount of money in the account after 5 years with monthly compounding is approximately $866.61.

Comparing the results from part 2 and part 4, we observe a slight difference in the amounts. With continuous compounding, the balance after 5 years is $866.85, while with monthly compounding, it is $866.61. This difference arises from the compounding frequency. Continuous compounding assumes infinite compounding periods, resulting in a slightly higher balance compared to monthly compounding, which has a fixed number of compounding periods in a year. Therefore, we conclude that continuous compounding yields a slightly higher amount than monthly compounding over the same time period.


To learn more about equations click here: brainly.com/question/29281557

#SPJ11

Answer:

  102,476

Step-by-step explanation:

If a population grows linearly from 55556 in 2000 to 72760 in 2011, you want the predicted value in 2030 assuming growth continues to be linear.

The change in population is proportional to the change in years:

  (72760 -55556)/(2011 -2000) = (p -55556)/(2030 -2000)

  p = 30(17204)/11 +55556 . . . . . . solve for p

  p = 46920 +55556 = 102,476 . . . . . . do the arithmetic

The population in 2030 will be $102,476.

Answer:

( 5.5 , 4 )

Step-by-step explanation:

Use mid point formula shown in image

first x= (X+X)/2

x=(4+7)/2

x=11/2

x=5.5

y=(Y+Y)/2

y=(2+6)/2

y=8/2

y=4

(5.5,4)

a) The evaporation rate per square foot of surface area (in gal/A) is equals to the 1/12 gal/A.

b) The thirty-three gallons of water will evaporate from a pool of 200 square feet.

We have, Area of a pool = 200 square feet

and we have to determine quantity of water evaporate from a pool in gallons. For this, first we have to calculate the evaporation rate. Let's assume y = gallons of water and

x = surface area in square foot

From the data, dy/dx = (50-25) / (400-100)

=> dy/dx = 1/12

The above equation means that for every 12 square feet surface there is 1 gallons water of evaporation will happen. So, similarly for 100 square feet = 100/12 gallons water

=> 8.33 gallons

But for 100 square feet 25 gallons of evaporation will happen.

=> 25 - 8.33 = 16.67

b) Now we will calculate quantity of water will evaporate from a pool of 200 square feet. As we know, 1 gallon for 12 square feet, so number of gallons for 200 square foot = 200/12

= 16.66

Now we add 16.67 for answer that is 16.66+ 16.67 = 33.33 ~ 33 gallons of water. Hence, required value is 33 gallons.

For more information about gallons, visit :

https://brainly.com/question/26007201

#SPJ4

Complete question:

Water evaporates from a swimming pool at an approximately constant rate of 25 gallons of water for a pool with a surface area of 100 square feet to 50 gallons for a pool with a surface area of 400 square feet.

(a) What is the evaporation rate per square foot of surface area (in gal/A?)? Round to the nearest hundredth. gal/

(b) How many gallons of water will evaporate from a pool of 200 square feet? Round to the nearest gallon. X gal Need Help? Read Submit Answer

Answer:

25000 mg.

Step-by-step explanation:

There are 1000 mg per gram.  If we multiply 1000*25 we will get 25000 mg of sugar.

There are 70 different types of pizzas could be ordered

A permutation is an act of arranging the objects or numbers in order.

Combinations are the way of selecting the objects or numbers from a group of objects or collection, in such a way that the order of the objects does not matter

Given,

Number of options on crust=2

Number of options on topping= 7

Number of options on size= 5

Therefore for each type of crust there are 7 different topping, for each toppings there are 5 different sizes

The total number ways of ordering pizza=2×7×5=70

Hence, there are 70 different types of pizzas could be ordered

Learn more about Combination here

brainly.com/question/13387529

#SPJ4

1.  A consequence of committing a Type I error is falsely rejecting a true null hypothesis.

2. A consequence of committing a Type II error is failing to reject a false null hypothesis.

a. A consequence of committing a Type I error is falsely rejecting a true null hypothesis.

In the given context, it would mean concluding that the AAA proportion of driver error causing fatal accidents is inaccurate (rejecting the null hypothesis) when it is actually accurate.

b. A consequence of committing a Type II error is failing to reject a false null hypothesis. In the given context, it would mean failing to conclude that the AAA proportion of driver error causing fatal accidents is inaccurate (failing to reject the null hypothesis) when it is actually inaccurate.

To determine if the AAA proportion is accurate, a hypothesis test can be conducted using the given sample data. The null hypothesis (H0) would state that the AAA proportion is accurate (54%), while the alternative hypothesis (Ha) would state that the AAA proportion is inaccurate.

Learn more about Null Hypothesis here:

https://brainly.com/question/30821298

#SPJ1

The Answer:the answer is D

Step-by-step explanation:

(a) tangent line to the graph of f(x) = x^3 at the point (4,2).

(b) equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12).

(a) To find the equation of the tangent line to the graph of f(x) = x^3 at the point (4,2), we need to find the slope of the tangent line at that point. We can do this by taking the derivative of f(x) with respect to x and evaluating it at x = 4. The derivative of f(x) = x^3 is f'(x) = 3x^2. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Once we have the slope, we can use the point-slope form of a linear equation to write the equation of the tangent line.

(b) Similarly, to find the equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12), we differentiate f(x) to find the derivative f'(x). The derivative of f(x) = x^2 - x is f'(x) = 2x - 1. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Using the point-slope form, we can write the equation of the tangent line.

In both cases, the equations of the tangent lines will be in the form y = mx + b, where m is the slope and b is the y-intercept.

Learn more about line tangent: brainly.com/question/30162650

#SPJ11

The three wffs given in this question all evaluate to true for all the given combinations of truth values.

Truth tables can be used to determine the truth values of logical expressions. The following truth tables represent the given three wffs (well-formed formulas):

a ~a b ~b (1) (a ⊃ (~a v ~b)) ⊃ (a v ~ b) (2) ( (a v b) & ((~a ⊃ b) ⊃ b)) ⊃ (a ⊃ ~b) (3) (a ⊃ b) v (~b v (a ⊃ ~ b))

T F T F T T T

T F F T T F T

F T T F F T T

F T F T T T F

From the truth tables, it is clear that (1) (a ⊃ (~a v ~b)) ⊃ (a v ~ b) is true for all the given combinations of truth values. Similarly, (2) ( (a v b) & ((~a ⊃ b) ⊃ b)) ⊃ (a ⊃ ~b) and (3) (a ⊃ b) v (~b v (a ⊃ ~ b)) are both true for all the given combinations of truth values.

To better understand how truth tables can be used to determine the truth values of logical expressions, we can look at the specific truth values assigned to the expressions. For (1) (a ⊃ (~a v ~b)) ⊃ (a v ~ b), the first part (a ⊃ (~a v ~b)) evaluates to true, regardless of the values of a and b. This means that the result of (1) will always be true. For (2) ( (a v b) & ((~a ⊃ b) ⊃ b)) ⊃ (a ⊃ ~b), the first part ((a v b) & ((~a ⊃ b) ⊃ b)) evaluates to true if a and b both have the same truth value. This means that the result of (2) will be true if a and b are both true or both false. For (3) (a ⊃ b) v (~b v (a ⊃ ~ b)), the first part (a ⊃ b) evaluates to true if a is true and b is false, and the second part (~b v (a ⊃ ~ b)) evaluates to true if b is false and a is true or false. This means that the result of (3) will be true if a and b are different truth values.

In conclusion, truth tables can be used to determine the truth values of logical expressions. The three wffs given in this question all evaluate to true for all the given combinations of truth values.

For more such questions on Truth tables.

https://brainly.com/question/29155453#

#SPJ11

Answer:

x = 7

y = 0

Step-by-step explanation:

use substitution method:

2(-6y + 7) - 9y = 14

-12y + 14 - 9y = 14

-21y = 0

y = 0

x = -6(0) + 7

x = 7

Step-by-step explanation:

Hey there!

Given eqautions are;

2x-9y= 14……………(i)

x= -6y+7………………(ii)

~ Putting the value of"x" from eqaution (ii) in eqaution (i).

2(-6y+7) - 9y = 14

~ Simplify it.

-12y +14 -9y= 14

21y = 0

y =0/21

Therefore, y= 0.

Now,

~ Put value of "x" on eqaution (ii).

X = -6(0)+7

x= (0)+7

x= 7

Therefore, x= 7.

Check:

Putting the value of X and y in eqaution (ii)

7= -6(0)+7

7=7(True).

x= 7

y= 0

Hope it helps....

Answer:

\(\frac{2y-8x+3xy}{xy}\)

Step-by-step explanation:

cancel out the common factor (x^2) & (y^2)

Answer:

5.04 seconds

Step-by-step explanation:

According to the graph :

Observe the end points on x axis of the parabola

They are

Time is x axis

So total time

Step-by-step explanation:

Magnitude = sqrt ( (-12)^2 + (-4)^2 ) = sqrt 160 = 12.649

Angle = arctan(-4/-12) = 198 degrees

The Magnitude: 12.649 and Direction: 18° (option c).

To find the magnitude and direction of the vector v = (-12, -4), we can use the following formulas:

Magnitude (or magnitude) of v = |v| = √(vₓ² + \(v_y\)²)

Direction (or angle) of v = θ = arctan(\(v_y\) / vₓ)

where vₓ is the x-component of the vector and \(v_y\) is the y-component of the vector.

Let's calculate:

Magnitude of v = √((-12)² + (-4)²) = √(144 + 16) = √160 ≈ 12.649 (rounded to the thousandths place)

Direction of v = arctan((-4) / (-12)) = arctan(1/3) ≈ 18.435°

Since we need to round the direction to the nearest degree, the direction is approximately 18°.

So, the correct answer is:

Magnitude: 12.649 (rounded to the thousandths place)

Direction: 18° (rounded to the nearest degree)

The correct option is: 12.649; 18°

To know more about Magnitude:

https://brainly.com/question/31022175

#SPJ2

The predicted college gpa be for a student whose current high school

gpa = 3.2 is 2.9718.

In statistics, a scalar response and one or more explanatory factors are modeled using a linear approach called linear regression. Simple linear regression is the scenario in which there is only one explanatory variable; multiple linear regression is the scenario in which there are numerous explanatory variables.

When predicting a variable's value based on the value of another variable, linear regression analysis is utilized. The dependent variable is the one you're trying to forecast. The independent variable is the one that you are utilizing to forecast the value of the other variable.

The linear regression for Y (dependent variable) on X (independent variable) is given by:

Y = a + bX

where,

a be the y-intercept

b be the slope of the line

When the slope is positive (or negative), the regression line is presumed to be increasing, which gives rise to the characteristics for the assumption (or decreasing).

For a = 0.719, b = 0.704, and X = 3.2, the predicted college GPA exists,

Y′ = 0.719 + (0.704 \(*\) 3.2) = 2.9718

Therefore, the predicted college gpa be for a student whose current high school gpa = 3.2 is 2.9718.

To learn more about linear regression refer to:

https://brainly.com/question/25987747

#SPJ4

Answer:

4km/1.5km

Step-by-step explanation:

hope that helps :)

Ratio of 400m to 1.5km​ is 400/1500 or 400:1500

A ratio is an ordered pair of numbers a and b, written a / b where b does not equal 0.

Here the given quantities are 400m and 1.5km

The quantities are with different unit

We convert them into same unit

We know that one kilometre=1000 metre

One kilometre equal to thousand metres.

Let us convert 1.5 km to metre by multiplying 1.5 with 1000

1.5×1000=1500

The ratio of 400m to 1.5km​ is 400/1500 or 400:1500

Hence  ratio of 400m to 1.5km​ is 400/1500 or 400:1500

To learn more on Ratios click:

https://brainly.com/question/1504221

#SPJ2

the solution of equation problem is estimated distance of the gold medal winning discus throw in 1980 is approximately 65.03 meters. The answer is option C.

An equation is a statement that says two things are equal. It can contain variables, which can take on different values. Equations are used to solve problems and model real-world situations by expressing relationships between variables.

A mathematical definition of an equation is a claim that two expressions are equal when they are joined by the equals sign ("="). For illustration, 2x - 5 = 13.

Here,

5 and 13 are expressions for 2x.

These two expressions are joined together by the sign "="

To estimate the distance of the gold medal winning discus throw in 1980 using the line of best fit, we need to first calculate the value of x for the year 1980

x = 1980 - 1920 = 60

Now, we can substitute x=60 into the equation of the line of best fit to find the estimated distance:

y = 0.34x + 44.63

y = 0.34(60) + 44.63

y = 20.4 + 44.63

y ≈ 65.03

Therefore, the estimated distance of the gold medal winning discus throw in 1980 is approximately 65.03 meters. The answer is option C.

To know more about Equation visit :-

https://brainly.com/question/15172156

#SPJ1

Answer: 17/y-5

Step-by-step explanation:

The slopes of the secant lines are listed below:

Case I: m = 0

Case II: m = - √3  (aprox. 1.7321)

Case III: m = 0

Case IV: m = 2.2103

Case V: m = 5√3 / 2 (approx. 4.3301)

Case VI: m = 7.5570

Case VII: m = 0

Case VIII: m = - √3  (aprox. 1.7321)

Case IX: m = 0

Case X: m = 5

Case XI: m = - 9.8480

In this problem we find eleven cases of two pairs of points lying on a sinusoidal curve, each of which we need to determine the slope of the secant line by means of the following formula:

m = [f(a) - f(b)] / (b - a)

Where the definition of the sinusoidal function is f(x) = sin (14π / x).

Now we proceed to determine the slope of each secant line:

Case I

m = [f(2) - f(1)] / (2 - 1)

m = (0 - 0)

m = 0

Case II

m = [f(1.5) - f(1)] / (1.5 - 1)

m = (- √3 / 2 - 0) / 0.5

m = - √3  (aprox. 1.7321)

Case III

m = [f(1.4) - f(1)] / (1.4 - 1)

m = (0 - 0) / 0.4

m = 0

Case IV

m = [f(1.3) - f(1)] / (1.3 - 1)

m = (0.6631 - 0) / 0.3

m = 2.2103

Case V

m = [f(1.2) - f(1)] / (1.2 - 1)

m = (√3 / 2 - 0) / 0.2

m = 5√3 / 2 (approx. 4.3301)

Case VI

m = [f(1.1) - f(1)] / (1.1 - 1)

m = (0.7557 - 0) / 0.1

m = 7.5570

Case VII

m = [f(0.5) - f(1)] / (0.5 - 1)

m = (0 - 0) / (- 0.5)

m = 0

Case VIII

m = [f(0.6) - f(1)] / (0.6 - 1)

m = (- √3 / 2 - 0) / (- 0. 4)

m = - √3  (aprox. 1.7321)

Case IX

m = [f(0.7) - f(1)] / (0.7 - 1)

m = (0 - 0) / (- 0. 3)

m = 0

Case X

m = [f(0.8) - f(1)] / (0.8 - 1)

m = (- 1 - 0) / (- 0.2)

m = 5

Case XI

m = [f(0.9) - f(1)] / (0.9 - 1)

m = (- 0.9848 - 0) / (- 0.1)

m = - 9.8480

To learn more on slopes of secant lines: https://brainly.com/question/14438198

#SPJ1

The confidence interval which shows 90% confidence level for the mean and assumed standard deviation is (2.94 meals, 3.0565 meals).

Given standard deviation=1.4. Sample size =1271, mean=3.

We have to find the confidence interval for 90% confidence level.

We have to find out α level that is the subtraction of 1 by the confidence interval divided by 2.

α=(1-0.90)/2

=0.05

Now we have to find z in the z table as such z has a p value of 1-α so it is z with p value of 1-0.05=0.95

Z=1.44 from z table.

Now find M as such that

M=z* st/\(\sqrt{n}\)

where st is standard deviation ,n is sample size.

M=1.44*1.4/\(\sqrt{1271}\)

=1.44*1.4/35.65

=2.016/35.65

=0.0565

Lower end= mean -M

=3-0.0565

=2.94

Upper end=Mean+ M

=3+0.0565

=3.0565

Hence the confidence interval showing 90% confidence level is (2.94,3.0565).

Learn more about z test at https://brainly.com/question/14453510

#SPJ4

The function t(x, y) = (2x², 3xy, y²) is not a linear transformation because it does not satisfy the additivity condition.

To determine whether the function t: ℝ² → ℝ³ defined as t(x, y) = (2x², 3xy, y²) is a linear transformation, we need to check two conditions: additivity and scalar multiplication.

Additivity:

Let's consider two vectors (x₁, y₁) and (x₂, y₂) in ℝ².

t(x₁, y₁) = (2x₁², 3x₁y₁, y₁²)

t(x₂, y₂) = (2x₂², 3x₂y₂, y₂²)

Now, let's add the two vectors and calculate t(x₁, y₁) + t(x₂, y₂):

t(x₁, y₁) + t(x₂, y₂) = (2x₁², 3x₁y₁, y₁²) + (2x₂², 3x₂y₂, y₂²)

                      = (2x₁² + 2x₂², 3x₁y₁ + 3x₂y₂, y₁² + y₂²)

If we calculate t(x₁ + x₂, y₁ + y₂), we get:

t(x₁ + x₂, y₁ + y₂) = (2(x₁ + x₂)², 3(x₁ + x₂)(y₁ + y₂), (y₁ + y₂)²)

                    = (2x₁² + 4x₁x₂ + 2x₂², 3x₁y₁ + 3x₁y₂ + 3x₂y₁ + 3x₂y₂, y₁² + 2y₁y₂ + y₂²)

Comparing t(x₁ + x₂, y₁ + y₂) and t(x₁, y₁) + t(x₂, y₂), we can see that the two expressions are not equal. Therefore, the additivity condition is not satisfied, and the function t is not additive.

Since t does not satisfy additivity, it cannot be a linear transformation.

To know more about linear transformation refer here:

https://brainly.com/question/13595405#

#SPJ11

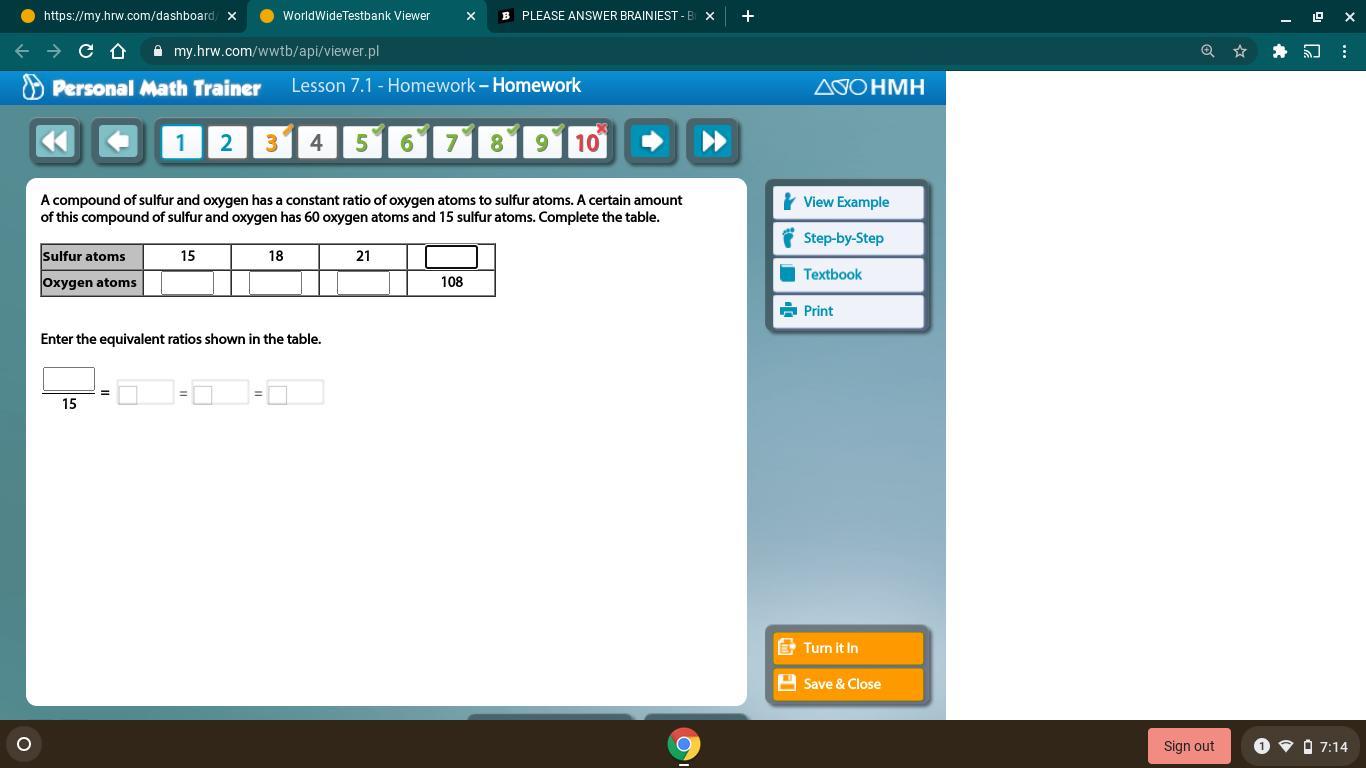
Answer:

Step-by-step explanation:

15:60

your ratio would be a 1:4

15  18  21  27

60  72  84  108

Answer:1560

Step-by-step explanation: i just copied the other guy