A student is writing a proof that if n >1 and n is a natural number then n3 – n is divisible by 6. Write down, using an equation, (meaning use an equals sign what the inductive hypothesis would be. Do NOT write a full proof, just write the inductive hypothesis, P(k).)
Answers
The inductive hypothesis, P(k), states that if the equation k³ - k is divisible by 6 for some natural number k > 1, then it also holds true for the next natural number, k+1.
The inductive hypothesis, denoted as P(k), would be:
Assuming that for some natural number k > 1, the equation holds true:
k³ - k is divisible by 6.
In other words, P(k) states that if k³ - k is divisible by 6, then the equation also holds true for the next natural number, which is k+1. This hypothesis forms the basis for the inductive proof, where we will show that if P(k) is true, then P(k+1) is also true.
To know more about inductive hypothesis, refer to the link below:
https://brainly.com/question/31703254#
#SPJ11
Related Questions
Corey bought 2 1/2
liters of paint for 60dollars
What was the cost per liter of paint?
Answers
Answer:
24 dollars per liter
Step-by-step explanation:
Take the number of dollars and divide by the number of liters
60 dollars / 2.5 liters
24 dollars per liter
Answer:$24 per litter
Step-by-step explanation:
What type of pair of angles are∠2 and angle∠11 ?
Answers
The type of pair of angles that are∠2 and angle∠11 is an alternate interior angles.
What is an alternate interior angle?When a transversal intersects two coplanar lines, alternate interior angles are formed. They are on the inside of the parallel lines, but on the outside of the transversal.
Angles with the same size that occur on opposite sides of the transversal line are known as alternate angles. The following alternate angles are equal: By drawing a Z shape, we can frequently identify interior alternate angles: Alternate angles are classified into two types: alternate interior angles and alternate exterior angles.
To understand alternate interior angles, imagine a set of parallel lines and then a line intersecting them. The intersecting line is known as a transversal, and all of the angles formed by the parallel lines are known as interior angles.
Both angles are interior angles that lie alternately to each other on the transversal line r. Therefore, they are alternate interior angle.
Learn more about angle on:
https://brainly.com/question/25716982
#SPJ1

(03.02 MC)The number of pages that Ana, Hillary, Roger, and Juan can read in a day is shown below:
Ana read 15% of her 46-page book.
Hillary read 11% of her 72-page book.
Roger read 12% of his 68-page book.
Juan read 14% of his 69-page book.
Who can read the greatest number of pages in a day?
plz explain your answer
Answers
Answer:
Juan
Step-by-step explanation:
The number of pages that Ana, Hillary, Roger, and Juan can read in a day is shown below:
For Ana
Ana read 15% of her 46-page book.
= 15% × 46 pages
= 6.9 pages
For Hillary
Hillary read 11% of her 72-page book.
= 11% × 72 pages
= 7.92 pages
For Roger
Roger read 12% of his 68-page book.
= 12% × 68 pages
= 8.16 pages
For Juan
Juan read 14% of his 69-page book.
= 14% × 69 pages
= 9.66 pages
The person who can read greatest number of pages in a day also means the person who read the highest number of pages in a day.
From the calculation above, that person in JUAN because she can read 9.66 pages of her book in one day.
Answer:
juan or D
Step-by-step explanation:
took the test
would
you help me with this abstract algebra question?
I need a detailed explanation.
Thank you!
Concepts: Basic concepts emphasized: - Rings, definition and examples. - Commutativity, unity, subrings, units, division.
5. Write down a multiplication table for the ring: \[ \mathbb{Z}_{2}[\sqrt{-2
Answers
The multiplication table for the ring \(\(\mathbb{Z}_2[\sqrt{-2}]\)\) cannot be provided without the actual elements of the ring.
To construct the multiplication table for the ring \((\mathbb{Z}_2[\sqrt{-2}]\)\), we need to know the elements of the ring. However, without the specific elements, we cannot generate the complete multiplication table.
The ring\(\(\mathbb{Z}_2[\sqrt{-2}]\)\) is formed by extending the integers modulo 2 \((\(\mathbb{Z}_2\))\) with the elemen\(t \(\sqrt{-2}\)\). Since we are working modulo 2, the elements in this ring can only take on the values 0 and 1.
To illustrate the general structure, we can represent the elements as\(\(a + b\sqrt{-2}\), where \(a, b \in \mathbb{Z}_2\)\) . The addition operation is performed modulo 2, and the multiplication operation follows the rules\(\((\sqrt{-2})^2 \equiv 0 \pmod{2}\)\).
To construct the multiplication table, we would list all possible combinations of elements and perform the multiplication operation. However, without knowing the specific elements, we cannot provide the complete multiplication table.
In summary, the multiplication table for the ring \(\(\mathbb{Z}_2[\sqrt{-2}]\)\) cannot be generated without the knowledge of the specific elements within the ring.
Learn more about Multiplication from the given link :
https://brainly.com/question/1135170
#SPJ11
(2x + 3)/5 = (x - 2)/3
What is x?
Answers
Helppppppol PLS NEED
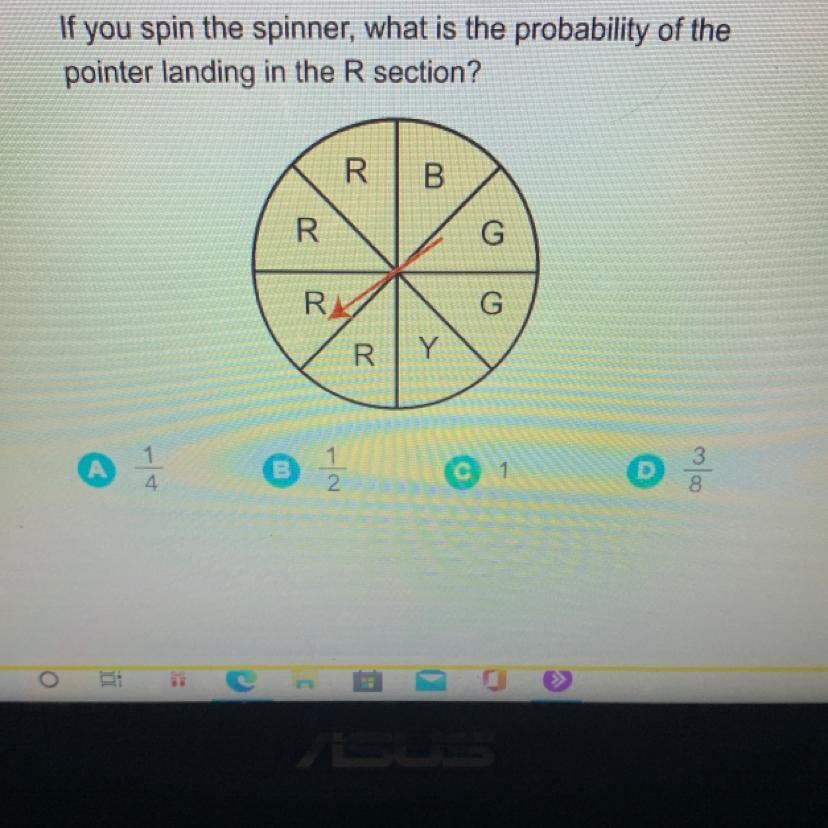
Answers
Answer:
the answer should be B)1/2
Step-by-step explanation:
there are 4 spots to land on R and 8 spots in total so it is 4/8 and when you simplify it comes out as 1/2
Which is an equation of the line through (0, 0) and (2, –3)?A.y=−23xy=− 32 xB.y=32xy= 23 xC.y=−32xy=− 23 xD.y=23xy= 32 x
Answers
The equation of the line passing through (0, 0) and (2, –3) is y = - 3 / 2 x
How to find the equation of a line?The equation of a line can be described as follows:
y = mx + b
where
m = slopeb = y-interceptTherefore, using (0, 0)(2, -3)
m = y₂ - y₁ / x₂ - x₁
m = -3 - 0 / 2 - 0
m = - 3 / 2
Therefore, the y-intercept is 0.
The equation of the line is y = - 3 / 2 x
learn more on equation of line here: https://brainly.com/question/12810609
#SPJ1
HELP WHAT IS THE VALUE OF TAN A

Answers
Answer: 4 / 3
Step-by-step explanation:
Soh Cah Toa
In this case, we'll use Toa
Tangent = Opposite / Adjacent
Tan A = 40 (opposite) / 30 (adjacent)
Tan A = 40 / 30 = 4 / 3 (simplified)
I need help!! im stuck and dont understand and this is due at 12

Answers
Answer:
K is the midpoint of JL.
I hope this helps:)
This distance time graph represents a journey made by Sue.
Work out how much time Sue spends travelling and how much time she spends stationary.
If, this doesn't make sense then see picture attached.
Please help me
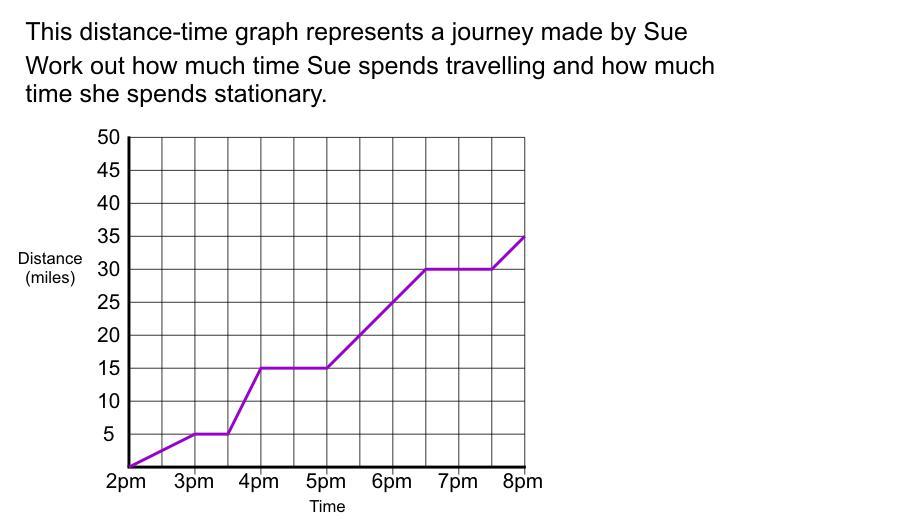
Answers
Answer:
stationary time is 2 hours 30 minutes
Traveling time is 3 hours 30 minutes
Step-by-step explanation:
There are two distinct line types on the graph
the horizontal ones and the ones going towards the upper part
The horizontal ones represent the stationary positions while the climbing one represent the traveling time
The horizontal ones are;
3 to 3:30
4-5
6:30 to 7:30
Time here is ;
30
minutes + 1 hour + 1 hour = 2 hours 30 minutes
The traveling time;
2 - 3
3:30 to 4
5 to 6:30
7:30 to 8
1 + 30 min + 1hr 30 + 30
= 3 hours 30 minutes
Answer:
Travelling-3 hours 30 minutes
Stationary-2.5 hours
Step-by-step explanation:
If x+4/4 = y+7/7 then x/4 =___.
(Number 9 is the one I need an answer for)

Answers
Answer:
4th answer is correct
Step-by-step explanation:
First, let us make x the subject.
\(\sf \frac{x+4}{4} =\frac{y+7}{7}\)
Use cross multiplication.
\(\sf 7(x+4)=4(y+7)\)
Solve the brackets.
\(\sf 7x+28=4y+28\)
Subtract 28 from both sides.
\(\sf 7x=4y+28-28\\\\\sf7x=4y\)
Divide both sides by 7.
\(\sf x=\frac{4y}{7}\)
Now let us find the value of x/4.
To find that, replace x with (4y/7).
Let us find it now.
\(\sf \frac{x}{4} =\frac{\frac{4y}{7} }{4} \\\\\sf \frac{x}{4} =\frac{4y}{7}*\frac{1}{4} \\\\\sf \frac{x}{4} =\frac{4y}{28}\\\\\sf \frac{x}{4} =\frac{y}{7}\)
you scored 85 percent on your math quiz. the quiz was out of 40 points how many points did you get
Answers
Answer: Said person scored 34 points on their math quiz.
Step-by-step explanation: To identify how many points the person got, what we need to do is multiply 40 by 0.85 because 85% is less than a whole, which would be 100.
40 x 0.85 = 34
Final answer: Out of the 40 maximum points, the person scored 34 points on their math quiz.
Answer:
34
Step-by-step explanation:
First, divide 85 by 100 to get 0.85. Then, multiply the percent (in decimal form) by 40 to get the answer 34.
Your cousin is bulding a sandbox for his daughter. How much sand will he need to fill the box? Explain. How much paint will he need to paint all six surfaces of the sandbox? Explain.
Answers
The amount of paint that he will need to paint all six surfaces of the sandbox is: 68 square feet
How to find the volume of the prism?Since the image is a rectangular prism
The volume of the box can be obtained by using the formula:
Volume = l * b * h
The box has a dimension of 1ft x 4ft x 6ft
The volume of the box = 1 x 4 x 6 = 24 cubic feet
Therefore, the volume of sand needed to fill the box will be = 24 cubic feet of sand
The surface area of the box can be obtained using the formula:
2(lb + lh + bh)
= 2(1*4 + 1*6 + 4*6)
=2(4 + 6 + 24)
=2 (34)
= 68 square feet
Therefore a total surface area of 68 square feet needs to be painted
Read more about Volume of box at: https://brainly.com/question/463363
#SPJ1
Complete question is:
Your cousin is building a Sandbox for his daughter how much sand will he need to fill the Box? Explain. How much paint will he need to paint all six surface of the sandbox? Explain. 1ft 4ft 6ft not answer choices
3. the chattanooga choo choo provides services for 4,500 tourists in a 30-day (month) period. the next month they provide services for 6355 tourists in a 31-day (month) period. what is the daily percent of increase in tourists from one month to the next? round to the nearest tenth of a percent.
Answers
The daily percent of increase in tourists from one month to the next is approximately 5.4% which is obtained through mathematical operations.
To calculate the daily percent of increase, we need to determine the difference in the number of tourists between the two months and divide it by the number of days in the second month. Then, we express this difference as a percentage.
In the given scenario, the increase in tourists from the first month to the second month is 6355 - 4500 = 1855. The number of days in the second month is 31. Dividing the increase by the number of days gives us
1855 / 31 = 59.8387.
To express this increase as a percentage, we multiply the result by 100, yielding 5983.87%. Rounding this to the nearest tenth of a percent gives us approximately 5983.9%.
Finally, to find the daily percent of increase, we divide the percentage by the number of days in the second month: 5983.9% / 31 = 5.4%.
Therefore, the daily percent of increase in tourists from one month to the next is approximately 5.4%.
Learn more about mathematical operations here:
https://brainly.com/question/25828217
#SPJ11
" Question set 2: Find the Fourier series expansion of the function f(x) with period p = 21
1. f(x) = -1 (-2
2. f(x)=0 (-2
3. f(x)=x² (-1
4. f(x)= x³/2
5. f(x)=sin x
6. f(x) = cos #x
7. f(x) = |x| (-1
8. f(x) = (1 [1 + xif-1
9. f(x) = 1x² (-1
10. f(x)=0 (-2
Answers
The Fourier series expansions of the given functions are as follows: f(x) = -1, f(x) = 0, f(x) = x², f(x) = x³/2, f(x) = sin(x) , f(x) = cos(#x) , f(x) = |x|, f(x) = (1 [1 + xif-1 , f(x) = 1x² (with calculated coefficients), and f(x) = 0.
The Fourier series expansion of a function is a representation of the function as a sum of sinusoidal functions. For the given function f(x) with a period p = 21, let's find the Fourier series expansions:
f(x) = -1:
The Fourier series expansion of a constant function like -1 is simply the constant value itself. Therefore, the Fourier series expansion of f(x) = -1 is -1.
f(x) = 0:
Similar to the previous case, the Fourier series expansion of the zero function is also zero. Hence, the Fourier series expansion of f(x) = 0 is 0.
f(x) = x²:
To find the Fourier series expansion of x², we need to determine the coefficients for each term in the expansion. By calculating the coefficients using the formulas for Fourier series, we can express f(x) = x² as a sum of sinusoidal functions.
f(x) = x³/2:
Similarly, we can apply the Fourier series formulas to determine the coefficients and express f(x) = x³/2 as a sum of sinusoidal functions.
f(x) = sin(x):
The Fourier series expansion of a sine function involves only odd harmonics. By calculating the coefficients, we can express f(x) = sin(x) as a sum of sine functions with different frequencies.
f(x) = cos(#x):
The Fourier series expansion of a cosine function also involves only even harmonics. By calculating the coefficients, we can express f(x) = cos(#x) as a sum of cosine functions with different frequencies.
f(x) = |x|:
The Fourier series expansion of an absolute value function like |x| can be obtained by considering different intervals and their corresponding expressions. By calculating the coefficients, we can express f(x) = |x| as a sum of different sinusoidal functions.
f(x) = (1 [1 + xif-1:
To find the Fourier series expansion of this function, we need to determine the coefficients for each term in the expansion. By calculating the coefficients using the formulas for Fourier series, we can express f(x) = (1 [1 + xif-1 as a sum of sinusoidal functions.
f(x) = 1x²:
Similar to the case of x², we can apply the Fourier series formulas to determine the coefficients and express f(x) = 1x² as a sum of sinusoidal functions.
f(x) = 0:
As mentioned before, the Fourier series expansion of the zero function is also zero. Therefore, the Fourier series expansion of f(x) = 0 is 0.
Each expansion represents the original function as a sum of sinusoidal functions, with different coefficients determining the amplitudes and frequencies of the harmonics present in the series.
To learn more about Fourier series here brainly.com/question/30763814
#SPJ11
a marble is selected from a bag containing eight marbles numbered to . the number on the marble selected will be recorded as the outcome. consider the following events. event : the marble selected has a number less than . event : the marble selected has an even number. give the outcomes for each of the following events. if there is more than one element in the set, separate them with commas.
Answers
Event A and B = 4
Event A or B = 2, 3, 4, 5, 6, 8
Complement of Event B = 1, 2, 7, 8
Event A: The marble selected has an even number.
The even numbers from 1 to 8 are 2, 4, 6, and 8. Therefore, the outcomes for Event A are: 2, 4, 6, 8.
Event B: The marble selected has a number from 3 to 6.
The numbers from 3 to 6 are 3, 4, 5, and 6. Therefore, the outcomes for Event B are: 3, 4, 5, 6.
Event A and B:
The outcomes that satisfy both Event A and Event B are the numbers that are both even and from 3 to 6. In this case, the only number that satisfies both conditions is 4.
Therefore, the outcome for Event A and B is: 4.
Event A or B:
The outcomes for Event A or Event B are the numbers that satisfy either Event A or Event B or both.
Combining the outcomes from Event A and Event B, we have: 2, 3, 4, 5, 6, 8.
Complement of Event B:
The complement of an event includes all the outcomes that are not part of the event.
In this case, the complement of Event B includes the numbers that are not from 3 to 6.
Therefore, the outcomes for the complement of Event B are: 1, 2, 7, 8.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ4
Complete question
A marble is selected from a bag containing eight marbles numbered 1 to 8.
The number on the marble selected will be recorded as the outcome.
Consider the following events.
Event A: The marble selected has an even number.
Event B: The marble selected has a number from 3 to 6.
Give the outcomes for each of the following events.
If there is more than one element in the set, separate them with commas.
Event A and B =
Event A or B =
Complement of the event B=
Can someone help me with this math homework please!

Answers
Answer:
Table 2.
Step-by-step explanation:
Recall that by definition, a linear function increases linearly. That is, the rate of change between any two points is constant.
We can go through each table and verify its rate of change.
Table 1)
For Table 1, note that y = -19 when x = 0.
When x = 1, y = -11. In other words, we added 8 for every increase of one for x.
When x = 2, y = -3. We still increased by 8 for every increase of one for x.
When x = 3, y = 5. Since -3 + 8 = 5, all points in Table 1 shows a constant rate of change.
In conclusion, Table 1 represents a linear function.
Table 2)
For Table 2, note that y = -1.5 when x = 0.
When x = 1, y = -1.5. In other words, we increased by 3 for every increase of one for x.
However, when x = 2, y = 3. This time, we only increased by 1.5 for every increase of one for x. Since the two rates are not equivalent, Table 2 is nonlinear.
Table 3)
Again, note that for Table 3, y = 15 when x = 0.
When x = 1, y = 12. So, we decreased by 3 for every increase of one for x.
When x = 2, y = 9. And when x = 3, y = 6. For both cases, we still decreased by 3 for every increase of one for x.
In conclusion, Table 3 represents a linear function.
Therefore, the table that represents a nonlinear function is Table 2.
find the inverse of the matrix (if it exists). (if an answer does not exist, enter dne.) 4 5 7 9
Answers
The inverse of the given matrix does not exist. To determine if the inverse of a matrix exists, we need to check if the matrix is invertible, which is equivalent to checking if the matrix has a nonzero determinant.
The given matrix is a 2x2 matrix with elements 4, 5, 7, and 9. To calculate the determinant, we multiply the diagonal elements and subtract the product of the off-diagonal elements. In this case, the determinant is (4 * 9) - (5 * 7) = 36 - 35 = 1. Since the determinant is nonzero, we conclude that the matrix is invertible. However, to find the inverse of the matrix, we need to calculate the matrix of cofactors, transpose it, and divide by the determinant.
Learn more about determinant here: brainly.com/question/14405737
#SPJ11
PLLLLLLLLLLLLLLLEEEEEEEEEAAAAAAAASSSSSSSE HEEEEEEEEELP As soon as a new car that costs $25,000 is driven off the lot, it begins to depreciate at a rate of 24.9% annually. About how much money is the car worth after the second year?
Answers
Answer:
The value of the car after two years is $14,100.025
Step-by-step explanation:
Here, we want to calculate the value of a car after its second year, given the depreciation percentage.
To get the value of the car year after year at the fixed percentage level, what we do is to set up an exponential equation;
V = I(1-r)^t
where V is the present value
I is the initial value = $25,000
r is the rate = 24.9% = 24.9/100 = 0.249
t is the number of years = 2 in this case
So we substitute these values in the depreciation case and have;
V = 25000(1-0.249)^2
V = 25000(0.751)^2
V = $14,100.025
Provide an example of a regression that arguably would have a high value of R 2
but would produce biased and inconsistent estimators of a causal effect. Explain why the R 2
is likely to be high. Explain why the OLS estimators would be biased and inconsistent.
Answers
An example of a regression that arguably would have a high value of R2 but would produce biased and inconsistent estimators of a causal effect is a regression of income against age. The R2 is likely to be high because income tends to increase with age. However, the OLS estimators would be biased and inconsistent because there are other factors that affect income besides age.
Regression models seek to analyze relationships between variables. A high R2 indicates a good fit of the model and suggests that a large part of the variation of the dependent variable is explained by the independent variables. In the regression of income against age, age is the independent variable and income is the dependent variable.
The R2 in this regression is likely to be high because income tends to increase with age due to factors such as experience, promotions, and seniority. The OLS estimators, on the other hand, would be biased and inconsistent because there are other variables that affect income besides age.
For example, education level, location, and occupation are all factors that could affect income but are not included in the regression model. Therefore, the causal effect of age on income cannot be estimated accurately.
You can learn more about regression at: brainly.com/question/32505018
#SPJ11
develop an algorithm to determine the probability of winning the lottery after at least n trials. assume that you can only buy one ticket whose probability of winning the lottery in each trial is p. therefore, the probability of not winning with the same ticket is 1-p in each trial. also, the number of trials needed to win the lottery is represented by the random variable x. the formula to calculate the probability of winning the lottery after at least n trials is:
Answers
The probability of winning the lottery after at least n trials, we can use the formula: P(X≤ n) = 1 - (1-p)^n
Where X is the number of trials needed to win the lottery, p is the probability of winning the lottery in each trial, and n is the minimum number of trials we are considering.
To understand the above formula, we need to consider the probability of winning the lottery in each trial. Let's assume that the probability of winning the lottery in each trial is p. Therefore, the probability of not winning with the same ticket is 1-p in each trial.
Now, let's consider the random variable X, which represents the number of trials needed to win the lottery. If we want to calculate the probability of winning the lottery after at least n trials, we need to find the probability of winning in the first n trials, plus the probability of winning in the (n+1)th trial or any subsequent trial.
The probability of winning in the first n trials can be calculated using the binomial distribution formula, which is:
P(X=k) = (n choose k) * p^k * (1-p)^(n-k)
Where k is the number of trials in which we win the lottery.
However, we are interested in finding the probability of winning after at least n trials, which means that we need to consider all possible values of k greater than or equal to n. Therefore, we can use the cumulative distribution function (CDF) of the binomial distribution to calculate the probability of winning after at least n trials, which is:
P(X≥ n) = 1 - Σ P(X=k) for k=0 to n-1
This formula calculates the probability of winning the lottery in the first n-1 trials and subtracts it from 1 to get the probability of winning in the nth trial or any subsequent trial.
However, we are interested in the probability of winning after at least n trials, not just in the nth trial or any subsequent trial. Therefore, we can rewrite the above formula as:
P(X≤n) = 1 - P(X>n-1)
Which gives us the probability of winning the lottery after at least n trials, using the complement rule of probability.
Finally, substituting the binomial distribution formula in the above formula, we get:
P(X≤n) = 1 - (1-p)^n
This formula gives us the probability of winning the lottery after at least n trials, based on the probability of winning the lottery in each trial and the minimum number of trials we are considering.
Learn more about Probability:
brainly.com/question/32117953
#SPJ11
The demand equation for a certain product is 8p2 + q2 = 1800, where p is the price per unit in dollars and q is the number of units demanded. da (a) Find and interpret dp (b) Find and interpret dq dg (a) How is calculated? dp оооо A. Use implicit differentiation. Differentiate with respect to p and assume that p is a function of q. B. Use implicit differentiation. Differentiate with respect to q and assume that is a function of p. C. Use implicit differentiation. Differentiate with respect to q and assume that p is a function of q. D. Use implicit differentiation. Differentiate with respect to p and assume that is a function of p
Answers
a. the rate of change of price with respect to the demand for the product. It tells us how much the price changes when the demand changes by a small amount. b. the demand changes when the price changes by a small amount.
To find dp, we need to differentiate both sides of the equation with respect to p, assuming that q is a function of p.
So, differentiating both sides with respect to p, we get:
16p + 2q(dq/dp) = 0
Solving for dp, we get:
dp = - (q/8p) dq
Interpreting dp, we can say that it represents the rate of change of price with respect to the demand for the product. It tells us how much the price changes when the demand changes by a small amount.
(b) To find dq/dg, we need to differentiate both sides of the equation with respect to q, assuming that p is a function of q.
So, differentiating both sides with respect to q, we get:
16p(dp/dq) + 2q = 0
Solving for dq/dg, we get:
dq/dg = - 8p/q(dp/dq)
Interpreting dq/dg, we can say that it represents the rate of change of demand with respect to the price of the product. It tells us how much the demand changes when the price changes by a small amount.
Learn more about rate of change here
https://brainly.com/question/8728504
#SPJ11
what is the probability that an exponentially distributed random variable takes on a value within one standard deviation of its mean
Answers
Around 68% of values are within 1 standard deviation from the mean with the probability that an exponentially distributed random variable takes on a value within one standard deviation of its mean.
As the empirical rule says, or also know as the 68-95-99.7 rule, tells where most of the values lie in a normal distribution, with this we know that:
Around 68% of values are within 1 standard deviation from the mean.
And around 95% of values are within 2 standard deviations from the mean.
And around 99.7% of values are within 3 standard deviations from the mean.
The empirical rule is a quick way to get an overview of the data and check for any outliers or extreme values that don’t follow the pattern.
If data from small examples do not follow the pattern closely, then other distributions like the t-distribution must be more appropriate. Once the identification of the distribution of the variable is done, then appropriate statistical tests can be applied.
To learn more about empirical rule, click here:
brainly.com/question/30700783
#SPJ4
The dot plot shown represents the number of students enrolled in each of the 16 courses at a community college. A new course has started and has 65 enrolled students. Consider the effect of the addition of the new course to the data set. Choose True or False for each statement.
Answers
The mode of the number of students enrolled in the courses may or may not increase by adding the new course. Statement 5: False. The standard deviation of the number of students enrolled in the courses may or may not increase by adding the new course.
The dot plot provided is missing, please provide the relevant details so that we can help you with the question.The dot plot shown represents the number of students enrolled in each of the 16 courses at a community college. A new course has started and has 65 enrolled students.
The mean number of students enrolled in the courses will increase by adding the new course. Statement 2: False. The median number of students enrolled in the courses will not necessarily increase by adding the new course. Statement 3: False. The range of the number of students enrolled in the courses may not necessarily increase by adding the new course. Statement 4: False.
To know more about community visit:
https://brainly.com/question/29811467
#SPJ11
When the input is 5, what is the output for the square function?

Answers
Answer:25
Step-by-step explanation:
Answer:
20
Step-by-step explanation:
can you please help me?

Answers
Answer:
24.00
Step-by-step explanation:
8 times tables
someone pls help
asap
ty :)

Answers
Answer:
56%
Step-by-step explanation:
We know that there are 6 groups of 6 and 4 groups of 5.
6x6 = 36
4x5 = 20
Add them up. 36 + 20 = 56.
Add the percent sign for 56%.

Answer:
56%
Step-by-step explanation:
Please helpppppppppppppppppppppppppp

Answers
Answer:
the answer is D or A
Step-by-step explanation:
step-by-step explanation
I hope this helps
Radicals/Fractional Exponents on Integers

Answers
Answer:
b.....................
\(\sqrt[5]{5} \cdot \sqrt[5]{5^2} = 5^{1/5} \cdot 5^{2/5} = \boxed{5^{3/5}}\)
Which one is greater 5.3 or 5 1/3
Answers
Answer:
5 1/3 > 5.3
Step-by-step explanation:
1/3 = 0.333... so 5 1/3 > 5.3 as 5 1/3 = 5.333...
The fraction 5 1/3 is greater than 5.3.
What is a fraction?A number expressed as a quotient, in which a numerator is divided by a denominator. In a simple fraction, both are integers. A complex fraction has a fraction in the numerator or denominator. A fraction represented with its quotient and remainder is a mixed fraction.
For the given situation,
The decimal number is 5.3.
The mixed fraction is 5 1/3.
First, convert this fraction to a decimal number to check which is greater.
\(5\frac{1}{3}=\frac{16}{3}\)
⇒ \(5.33\)
On comparing these two decimals 5.33 and 5.3, we can conclude that 5 1/3 is greater than 5.3.
Learn more about the fractions here
https://brainly.com/question/1301963
#SPJ2