a swimming pool has a depth of 4 ft at the shallow end and 8 ft at the deep end. the bottom of the pool slopes downward at an angle of 5.7°. how long is the pool? round to the nearest foot.
Answers
To solve this problem, we need to use trigonometry. We can use the tangent function to find the length of the pool.
First, we need to find the difference in depth between the shallow end and the deep end:
8 ft - 4 ft = 4 ft
Next, we need to find the horizontal distance over which this depth change occurs. We can use the angle of 5.7° to find this distance:
tan(5.7°) = opposite/adjacent
opposite = difference in depth = 4 ft
adjacent = horizontal distance we want to find
Solving for adjacent, we get:
adjacent = opposite/tan(5.7°)
adjacent = 4/tan(5.7°)
adjacent ≈ 39.6 ft
Therefore, the length of the pool is approximately 40 feet (rounded to the nearest foot).
Learn more about length:
https://brainly.com/question/28108430
#SPJ11
Related Questions
For each function, determine the zeros. State the multiplicity of any multiple zeros. y=(x+1)(x-4)(3-2 x) .
Answers
The zeros of a function, also known as the roots or x-intercepts, are the values of the independent variable for which the function evaluates to zero. In other words, they are the values of x where the graph of the function crosses or intersects the x-axis.
To find the zeros of the function y = (x + 1)(x - 4)(3 - 2x), we set the function equal to zero and solve for x:
0 = (x + 1)(x - 4)(3 - 2x)
To find the zeros, we set each factor equal to zero and solve for x individually:
x + 1 = 0
> x = -1
x - 4 = 0
> x = 4
3 - 2x = 0
> 2x = 3
> x = 3/2
Therefore, the zeros of the function are x = -1,
x = 4, and
x = 3/2.
Now let's determine the multiplicity of any multiple zeros. Since the function is factored, we can determine the multiplicity by looking at the power or exponent of each factor.
In this case, all the factors are linear, which means each zero has multiplicity 1. Therefore, the zeros -1, 4, and 3/2 each have a multiplicity of 1.
To know more about x-intercepts visit:
https://brainly.com/question/3205106
#SPJ11
All the zeros have a multiplicity of 1.
To determine the zeros of the function y = (x+1)(x-4)(3-2x), we need to set y equal to zero and solve for x. The zeros of a function are the values of x that make the function equal to zero.
Step 1: Set y = 0
0 = (x+1)(x-4)(3-2x)
Step 2: Use the zero product property
The zero product property states that if a product of factors is equal to zero, then at least one of the factors must be zero. Therefore, we can set each factor equal to zero and solve for x separately.
x+1 = 0
x = -1
x-4 = 0
x = 4
3-2x = 0
-2x = -3
x = 3/2
So, the zeros of the function y = (x+1)(x-4)(3-2x) are -1, 4, and 3/2.
Now let's determine the multiplicity of any multiple zeros. The multiplicity of a zero indicates how many times the factor (x-a) appears in the factored form of the function. We can determine the multiplicity by observing the powers of each factor.
In this case, we have three factors: (x+1), (x-4), and (3-2x).
The factor (x+1) appears once, so its multiplicity is 1.
The factor (x-4) also appears once, so its multiplicity is 1.
The factor (3-2x) appears once, so its multiplicity is 1 as well.
Learn more about multiplicity from the given link:
https://brainly.com/question/29796184
#SPJ11
A test with hypotheses H0:μ=5, Ha:μ<5, sample size 36, and assumed population standard deviation 1.2 will reject H0 when x¯<4.67. What is the power of this test against the alternative μ=4.5?
A. 0.8023
B. 0.5715
C. 0.9993
D. 0.1977
Answers
The power of a statistical test is the probability of correctly rejecting the null hypothesis when the alternative hypothesis is true. In this case, the null hypothesis (H0) is that the population mean (μ) is equal to 5, and the alternative hypothesis (Ha) is that μ is less than 5.
To calculate the power of the test, we need to determine the critical value for the given significance level (α) and calculate the corresponding z-score. Since the alternative hypothesis is μ < 5, we will calculate the z-score using the hypothesized mean of 4.5.
First, we calculate the z-score using the formula: z = (x¯ - μ) / (σ / √(n)), where x¯ is the sample mean, μ is the hypothesized mean, σ is the population standard deviation, and n is the sample size.
z = (4.67 - 4.5) / (1.2 / √(36)) = 0.17 / (1.2 / 6) = 0.17 / 0.2 = 0.85
Next, we find the corresponding area under the standard normal curve to the left of the calculated z-score. This represents the probability of observing a value less than the critical value.
Using a standard normal distribution table or a calculator, we find that the area to the left of 0.85 is approximately 0.8023.
Therefore, the power of this test against the alternative hypothesis μ = 4.5 is approximately 0.8023, which corresponds to option A.
Learn more about area here: https://brainly.com/question/1631786
#SPJ11
plss help i’ll give brainliest thank you!

Answers
Answer:
36
Step-by-step explanation:
The formula of LCM is LCM(a,b) = ( a × b) / GCF (a,b)
The Greatest Common Factor of (9,12) = 3
Therefore
LCM of 9 and 12 = (9 × 12) / 3
= 108/3 = 36
LCM of 9 and 12 = 36
Irrespective of the method, the solution to our question LCM of 9 and 12 is the same.
Therefore, LCM of 9 and 12 is 36
What is the principal that will grow to $5100 in two years,
eight months at 4.3% compounded semi-annually? The principal is
$=
Answers
The principal that will grow to $5,100 in two years, eight months at 4.3% compounded semi-annually is approximately $4,568.20.
To find the principal that will grow to $5,100 in two years and eight months at 4.3% compounded semi-annually, you can use the formula for compound interest:
A = P(1 + r/n)^(nt)
where:
A = final amount ($5,100)
P = principal amount (what we're trying to find)
r = annual interest rate (4.3% or 0.043)
n = number of times interest is compounded per year (semi-annually, so 2)
t = time in years (2 years and 8 months or 2.67 years)
First, plug in the values:
$5,100 = P(1 + 0.043/2)^(2*2.67)
Next, solve for P:
P = $5,100 / (1 + 0.043/2)^(2*2.67)
P = $5,100 / (1.0215)^(5.34)
P = $5,100 / 1.11726707
P ≈ $4,568.20
The principal that will grow to $5,100 in two years, eight months at 4.3% compounded semi-annually is approximately $4,568.20.
Learn more about Compound Interest: https://brainly.com/question/14295570
#SPJ11
Find r, T, N, and B at the given value of t. Then find the equations for the osculating, normal, and rectifying planes at that value of t. r(t) = (cos t)i + (sin t)j - 5k, t = pi/2 r(pi/2) = (0)i + (1)j + (-5)k (Type exact answer, using radicals as needed.) T(pi/2) = (-1)i + (0)j + (0) k (Type exact answer, using radicals as needed.) N(pi/2) = (0)i + (-)j + (0)k (Type exact answer, using radicals as needed.) B(pi/2) = (0)i + (0)j + (1)k (Type exact answer, using radicals as needed.) Choose the correct equation for the osculating plane at t = pi/2. -y = -1 -x = 0 z = -5 Squareroot 3/2 x + 1/2 y = 5
Answers
the equations for the osculating, normal, and rectifying planes at t = pi/2 are:
Osculating plane: z = -j * (t - pi/2) - 5
Normal plane: y = -i * (t - pi/2) + 1
Rectifying plane: x = 1.
To find the values of r, T, N, and B at t = pi/2, we first need to calculate r(pi/2) and its derivatives.
r(t) = (cos t)i + (sin t)j - 5k
r(pi/2) = (cos(pi/2))i + (sin(pi/2))j - 5k
= 0i + 1j - 5k
= <0, 1, -5>
To find T(pi/2), we need to take the derivative of r(t) and evaluate it at t = pi/2.
r'(t) = (-sin t)i + (cos t)j + 0k
r'(pi/2) = (-sin(pi/2))i + (cos(pi/2))j + 0k
= -i
Since T(pi/2) is the unit tangent vector at t = pi/2, we need to normalize r'(pi/2) to get T(pi/2).
|T(pi/2)| = |r'(pi/2)| = |-i| = 1
T(pi/2) = r'(pi/2) / |r'(pi/2)|
= (-i) / 1
= -i
= <-1, 0, 0>
To find N(pi/2), we need to take the second derivative of r(t) and evaluate it at t = pi/2.
r''(t) = (-cos t)i - (sin t)j + 0k
r''(pi/2) = (-cos(pi/2))i - (sin(pi/2))j + 0k
= 0i - 1j + 0k
= <0, -1, 0>
Since N(pi/2) is the unit normal vector at t = pi/2, we need to normalize r''(pi/2) to get N(pi/2).
|N(pi/2)| = |r''(pi/2)| = |<0, -1, 0>| = 1
N(pi/2) = r''(pi/2) / |r''(pi/2)|
= <0, -1, 0> / 1
= <0, -1, 0>
To find B(pi/2), we can use the formula B = T x N, where x denotes the cross product.
B(pi/2) = T(pi/2) x N(pi/2)
= <-1, 0, 0> x <0, -1, 0>
= <0*0 - (-1)*0, 0*0 - 0*0, (-1)*(-1) - 0*0>
= <0, 0, 1>
Therefore, we have:
r(pi/2) = <0, 1, -5>
T(pi/2) = <-1, 0, 0>
N(pi/2) = <0, -1, 0>
B(pi/2) = <0, 0, 1>
To find the equations of the osculating, normal, and rectifying planes at t = pi/2, we can use the following formulas:
Osculating plane: r(pi/2) + [r'(pi/2) x r''(pi/2)] / |r'(pi/2)|^2 * (t - pi/2)
Normal plane: r(pi/2) + [r''(pi/2) x [r'(pi/2) x r''(pi/2)]] / |r''(pi/2)|^2 * (t - pi/2)
Rectifying plane: r(pi/2) x [r'(pi/2) x r''(pi/2)] / |r'(pi/2)|^2
Plugging in the values we found earlier, we get:
Osculating plane: (0)i + (1)j + (-5)k + [(-i) x <0, -1, 0>] / |-i|^2 * (t - pi/2)
= (0)i + (1)j + (-5)k - j * (t - pi/2)
Normal plane: (0)i + (1)j + (-5)k + [<0, -1, 0> x [-i x <0, -1, 0>]] / |<0, -1, 0>|^2 * (t - pi/2)
= (0)i + (1)j + (-5)k + (-i*(t - pi/2)
Rectifying plane: <0, 1, -5> x [-i x <0, -1, 0>] / |-i|^2
= <0, 1, -5> x <0, 0, -1>
= <1, 0, 0>
Therefore, the equations for the osculating, normal, and rectifying planes at t = pi/2 are:
Osculating plane: z = -j * (t - pi/2) - 5
Normal plane: y = -i * (t - pi/2) + 1
Rectifying plane: x = 1.
Note that these equations are in the form of a plane equation ax + by + cz = d, where a, b, c are the components of the normal vector to the plane, and d is the distance from the origin to the plane.
Visit to know more about Osculating plane:-
https://brainly.com/question/30781925
#SPJ11
Mrs. Johnson has 159 chickens that she puts in shelters at night to keep safe. She places 12 chickens in a shelter and continues putting this number of chickens in each shelter until she comes to the last one. How many chickens will Mrs. Johnson put in the last shelter? answers: 3,4,13,14
Answers
Answer:
3
Step-by-step explanation:
159-12=147-12=... keep going until you get to
15-12=3
least common denominator of 1/3 and 7/12
Answers
Least common denominator is the least common multiple of the given denominators.
Find the least common multiple of 3 and 12, this way:
The least common multiple of 3 and 12 is 12, which means that the least common denominator of 1/3 and 7/12 is 12.

The price of a car decreases by 35% to £13000.
What was the car worth before the decrease?
Help

Answers
Answer:
€20,000
Step-by-step explanation:
% decrease = (original price of the car - new price) ÷ original price × 100
Let "x' represents the original price before the decrease.
New price = €13,000
% decrease = 35%
Plug in the values into the equation
\( 35 = \frac{x - 13,000}{x}*100 \)
\( 35 = \frac{100x - 1,300,000}{x} \)
Multiply both sides by x
\( 35*x = \frac{100x - 1,300,000}{x}*x \)
\( 35x = 100x - 1,300,000 \)
Subtract 100x from both sides
\( 35x - 100x = 100x - 1,300,000 - 100x \)
\( -65x = -1,300,000 \)
Divide both sides by -65
\( \frac{-65x}{65} = \frac{-1,300,000}{65} \)
\( x = 20,000 \)
The car was worth €20,000 before the decrease.
when approaching an intersection, if you see a traffic sign in the shape of a triangle, the sign is
Answers
Answer:
A traffic sign in the shape of a triangle is a warning sign. These signs are typically yellow with black lettering or symbols and are used to warn drivers of upcoming hazards or changes in the road ahead. Some common warning signs include "Sharp Curve Ahead," "Deer Crossing," "Merge Ahead," and "Pedestrian Crossing."
Step-by-step explanation:
help help help help help

Answers
Answer:
y = 45
Step-by-step explanation:
y = 9x
input = 5
y = 9(5)
9(5) = 45
y = 45
you come across a bomb that is about to go off if you do not stop it! to neutralize the bomb, you must get exactly four gallons of water in the empty tub to which it is attached. the only equipment you have is one empty 3-gallon jug, one empty 5-gallon jug and an unlimited supply of water. there are no markings on the jugs or the tub. the only thing you know is that one jug is 3-gallon and the other jug is 5-gallon. the jugs have to be completely filled. you cannot make eyeball assumptions about a half-filled jug. you have to make sure you get exactly 4 gallons in the tub. what do you do?
Answers
Fill the 3-gallon jug all the way.
Pour those 3 gallons of water into the 5-gallon jug.
Fill the 3-gallon jug all the way again, and pour as much as it takes to fill the 5-gallon jug (which is 2 gallons).
Now you have 5 gallons in the 5-gallon jug and 1 gallon in the 3-gallon jug.
Empty the 5-gallon jug.
Pour the 1 gallon in the 3-gallon jug into the 5-gallon jug.
Now fill the 3-gallon jug all the way, and pour all 3 gallons into the 5-gallon jug, which, added to the 1 gallon already in there, and leaves you with exactly 4 gallons.
To know more about Jug Problem visit brainly.com/question/16134180
#SPJ4
Fill the 3-gallon jug all the way.
Pour those 3 gallons of water into the 5-gallon jug.
Fill the 3-gallon jug all the way again, and pour as much as it takes to fill the 5-gallon jug (which is 2 gallons).
Now you have 5 gallons in the 5-gallon jug and 1 gallon in the 3-gallon jug.
Empty the 5-gallon jug.
Pour the 1 gallon in the 3-gallon jug into the 5-gallon jug.
Now fill the 3-gallon jug all the way, and pour all 3 gallons into the 5-gallon jug, which, added to the 1-gallon already in there, leaves you with exactly 4 gallons.
To know more about Jug Problem visit
brainly.com/question/16134180
#SPJ4
solve for c.
4(3+c)+c=c+4
Answers
Answer:
c=-2
Step-by-step explanation:
4(3+c)+c=c+4
distribute the 4
12+4c+c=c+4
subtract c on both sides
12+4c=4
subtract 12 on both sides
4c=-8
c=-2
Step-by-step explanation:
subtract c and distribute
12 + 4 c = 4
4c = - 8
solve for c
HELPPP!!!
(6 points)
8. If you bought a $55 table and
paid an additional $4 in tax,
what percentage was the tax?
Answers
Answer:
7.27%
Step-by-step explanation:
If the temperature continues to fall at this rate,what was the temperature after 1 hour
PLS ONLY ANSWER IF YOUR CORRECT THXX <3
Answers
Answer:
Incomplete question.
Provide the full question pls
Helpppppppppppppppp

Answers
4. If the radius of a circle is 24 feet, what is the diameter?
Answers
Answer: 12
Step-by-step explanation:
If the value of "y" varies directly with "x" and y = 6 when x = -2, find "y" when x = 8. Direct Variation Equation: y = kx
First, we'll solve for "k", the constant of variation. What value should we input for "y" in the equation?
A) 6
B) -2
C) 8
Answers
Answer:
to solve for k we will put y=6
A doggy daycare charges a $90 fee plus $15 each day to board a dog. the puppy palace charges $35 per day to board a dog. the cost to board the dog at each site is for a full day. how many days must someone board their dog for the total cost at a doggy daycare to be less expensive than puppy palace?
Answers
Answer:
5 days
Step-by-step explanation:
Answer:
All of theses are correct.
4.5
4 1/2
9/2
About 5.
mathematical literacy
\(79 \times 85\)
Answers
Answer:
6715
Step-by-step explanation:
I hope this helps, :)
HARDEST MATH PROBLEM!
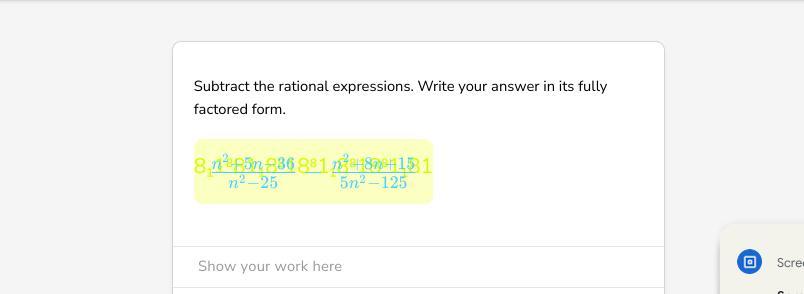
Answers
The result of subtracting and simplifying the rational expression in its fully factored form is \(\frac{4n^{2} +17n - 195 }{5(n^{2} -25)}\)
Simplifying an expression in fully factored formFrom the question, we are to subtract the rational expressions and express in the factored form
The given expression is
\(\frac{n^{2} + 5n - 36 }{n^{2} -25} - \frac{n^{2} +8n +15 }{5n^{2} -125}\)
Factor 5n² - 125
\(\frac{n^{2} +5n - 36 }{n^{2} -25} - \frac{n^{2} +8n +15 }{5(n^{2} -25)}\)
\(\frac{5(n^{2} +5n - 36) - (n^{2} +8n +15) }{5(n^{2} -25)}\)
\(\frac{5n^{2} +25n - 180 - n^{2} -8n -15 }{5(n^{2} -25)}\)
Simplify
\(\frac{4n^{2} +17n - 195 }{5(n^{2} -25)}\)
Hence, the expression is \(\frac{4n^{2} +17n - 195 }{5(n^{2} -25)}\)
Learn more on Simplifying an expression here: https://brainly.com/question/11792603
#SPJ1
Aditya’s boat has come untied and drifted a bit, and is now lodged against several rocks. Aditya is standing atop a cliff that is 35 ft. above the water in the lake. If she stands 10 ft. from the edge of the cliff, she can visually align the top of the cliff with the water at the back of her boat. Her eye level is 5.5 ft. above the ground. Her line of sight forms a 29° angle with the ground on the cliff, as well as with the water at the base of the boat.
Approximately how far out from the cliff is Aditya's boat? Round your answer to the nearest tenth of afoot. Show your work on paper or in the box below.
Aditya's boat is about ___feet from the cliff.
Answers
Approximately how far out from the cliff is Aditya's boat is 63.64ft.
DistanceGiven:
Standing atop a cliff above the water =35 ft
Standing at edge of the cliff=10ft
Eye level=5.5ft
Hence:
AE/CD=BC/DE
5.5/35=10/DE
AE=35×10/5.5
AE=350/5.5
AE=63.636ft
AE=63.64ft (Approximately)
Inconclusion approximately how far out from the cliff is Aditya's boat is 63.64ft.
Learn more about distance here:https://brainly.com/question/4931057

how much money will you earn if you get 3 million views on tlk tok or 3 million likes and or about 500k followers?
And how much money would you make per view/like?
Answers
Answer:
According to business insider, you can make an average of $0.01 to $0.02 for each sponsored view on TikTok. So if you have a video with 100,000 views, you can make 1000 dollars in sponsorships. After you have built a following on the app, you can reach out to brands and offer your services.He said that a creator with one million followers and good engagement should charge between $5,000 and $10,000 for a sponsorship on TikTok. That number is constantly shifting, however, as the platform matures.
Step-by-step explanation:
Enrollment in a dance studio has grown exponentially since the studio opened. A graph depicting this growth is shown. Determine the percentage rate of growth.
0.25%
1.25%
2.5%
25%

Answers
Answer:
Option (4). 25%
Step-by-step explanation:
The graph attached shows the exponential growth.
Let the graphed function is y = \((1+\frac{r}{100})^{t}\)
Here 'r' = Rate of growth
t = Duration of time in years
y = enrollments after time 't' years
Graph shows at time 't' = 0 or initially number of enrollments = 20
After 8 years number of enrollments will be
120 = \(20(1+\frac{r}{100})^{8}\)
\(\frac{120}{20}=(1+\frac{r}{100})^{8}\)
6 = \((1+\frac{r}{100})^{8}\)
log 6 = \(8\text{log}(1+\frac{r}{100})\)
0.77815 = \(8\text{log}(1+\frac{r}{100})\)
\(\text{log}(1+\frac{r}{100})\) = 0.0972689
\((1+\frac{r}{100})=1.251\)
\(\frac{r}{100}=0.251\)
r = 25.1%
r ≈ 25%
Therefore, Option (4) will be the answer.
Answer:
25%
Step-by-step explanation:
did test and it was right
Now, the Group of Good would like to decide how they should infiltrate the gallery. The group wants to vote on different plans to sneak into the gallery; the plans are labelled a - e. While the group puts all of the plans together so everyone can see them, a tragedy occurs. Kenny gets a paper cut by Plan a! The cut is too deep! Saddened by their colleague’s sudden paper death, they decide that the leader should have more say in which plan is picked (in hopes to avoid more unnecessary death). Suppose the leader’s vote (from the last question) counts as 5 votes. The following preference schedule is produced:
Total Votes = 2 2 1 1
Choice 1 e c a b b
Choice 2 d a b d a
Choice 3 c d e c d
Choice 4 a b d e c
Choice 5 b e c a e
(a) If plurality voting is used, what plan should the group use? Does this plan have a majority
Total Votes = 2 2 1 1
Choice 1 e c a b b
Choice 2 d a b d a
Choice 3 c d e c d
Choice 4 a b d e c
Choice 5 b e c a e
(b) If Instant Runoff Voting is used, what plan should the group use? Show how you discovered your answer.
Total Votes = 2 2 1 1
Choice 1 e c a b b
Choice 2 d a b d a
Choice 3 c d e c d
Choice 4 a b d e c
Choice 5 b e c a e
(c)If the Borda Count method is used, what plan should the group use? Show how the winner is computed
What was the best part of this project? What was the worst part?
Answers
(a) If plurality voting is used, Plan E will be chosen.
b It has the most first-place votes, with 2 each from voters 1 and 5. No other plan has more than 1 first-place vote.
c If the Borda Count method is used, Plan C will be chosen.
How to explain the informationa The best part of this project was learning about different voting methods and how they can be used to choose a winner. The worst part of the project was the difficulty of calculating the Borda Count.
b If Instant Runoff Voting is used, Plan C will be chosen. In the first round of counting, Plan E is eliminated, as it has the fewest first-place votes. In the second round, Plan C is eliminated, as it has the fewest second-place votes. In the third round, Plan B is eliminated, as it has the fewest third-place votes. In the fourth round, Plan D is eliminated, as it has the fewest fourth-place votes. This leaves Plan A as the winner, as it has the most votes remaining.
c If the Borda Count method is used, Plan C will be chosen. Each voter's ballot is assigned a number of points equal to the number of candidates ranked lower than that candidate. For example, voter 1's ballot gives Plan E 5 points, Plan C 4 points, Plan A 3 points, Plan B 2 points, and Plan D 1 point. The total number of points for each candidate is then calculated. Plan C has the most points, with 16, so it is the winner.
Learn more about plurality on
https://brainly.com/question/14581557
#SPJ4
The radius of a circle is 11 miles. What is the circle's area?
r=11 mi
Use 3.14 for d.
square miles
Submit

Answers
Not sure if you have to round or give an exact answer, but you can round that if you have to.
Answer:
379.94
Step-by-step explanation:
3.14 x (11x11) = 379.94
The provided dataset "Franchises Dataset" contains data collected from different 100 franchises. The data contains the net profit (million $) for each franchise, the counter sales (million $), the drive-through sales (million $), the number of customers visiting the business daily, and the type of the franchise. Q: What is the predicted profit of a Burger store restaurant with 900,000$ counter sales, and 800,000$ drive-through sales?
Answers
The predicted profit of a Burger store restaurant with $900,000 counter sales and $800,000 drive-through sales is $690,001 million.
To find the predicted profit of a Burger store restaurant with $900,000 counter sales and $800,000 drive-through sales using the provided dataset, we can follow these steps:
Step 1: Import the "Franchises Dataset" into a statistical software package like Excel or R.
Step 2: Perform regression analysis to find the equation of the line of best fit that relates the net profit (dependent variable) to the counter sales and drive-through sales (independent variables). The equation will be in the form of y = mx + b, where y is the net profit, x is the combination of counter sales and drive-through sales, m is the slope, and b is the y-intercept.
Step 3: Use the regression equation to calculate the predicted net profit for the given counter sales and drive-through sales values. Plug in the values of $900,000 for counter sales (x1) and $800,000 for drive-through sales (x2) into the equation.
For example, let's say the regression equation obtained from the analysis is: y = 0.5x1 + 0.3x2 + 1.
Substituting the values, we get:
Predicted Net Profit = 0.5(900,000) + 0.3(800,000) + 1
= 450,000 + 240,000 + 1
= 690,001 million dollars.
Therefore, the predicted profit of a Burger store restaurant with $900,000 counter sales and $800,000 drive-through sales is $690,001 million.
Learn more about profit at:
brainly.com/question/1078746
#SPJ11
(02.01)
Solve for x: 3x - 5 = 2x + 6. (1 point)
a
-1
d
-11
Answers
Answer:
Step-by-step explanation:
3x - 5 = 2x + 6
x - 5 = 6
x = 11
how to determine the end behavior of a rational function
Answers
By analyzing the degrees and leading coefficients, you can determine how the rational function behaves at the extreme ends of the x-axis.
To determine the end behavior of a rational function, you need to examine the degrees of the numerator and denominator polynomials. The end behavior refers to how the function behaves as the input (x-values) approaches positive or negative infinity.
Here are the steps to determine the end behavior of a rational function:
1. Identify the highest power of x in the numerator and denominator. Let's call them n and m, respectively.
2. If n < m, the degree of the denominator is greater than the numerator. In this case, the function's end behavior is determined by the degree of the denominator.
- If m is even, the function approaches the horizontal axis (y = 0) as x approaches both positive and negative infinity.
- If m is odd, the function approaches opposite infinities: positive infinity as x approaches negative infinity and negative infinity as x approaches positive infinity.
3. If n = m, the degree of the numerator is equal to the denominator. In this case, the leading coefficients of the numerator and denominator determine the end behavior.
- The function approaches the ratio of the leading coefficients as x approaches both positive and negative infinity.
4. If n > m, the degree of the numerator is greater than the denominator. In this case, the function's end behavior is determined by the degree of the numerator.
- If n is even, the function approaches positive infinity as x approaches both positive and negative infinity.
- If n is odd, the function approaches opposite infinities: positive infinity as x approaches positive infinity and negative infinity as x approaches negative infinity.
By analyzing the degrees and leading coefficients, you can determine how the rational function behaves at the extreme ends of the x-axis.
Learn more about rational function here
https://brainly.com/question/29098201
#SPJ4
Evaluate the following integral using trigonometric substitution. x² dx (225+x²)² What substitution will be the most helpful for evaluating this integral? A. x= 15 sin 0 B. x 15 tan 0 OC. x= 15 sec 0 Rewrite the given integral using this substitution. dx JC de (225+x²)2 (Type an exact answer.) =
Answers
To evaluate the given integral, the most helpful substitution is x = 15 sec θ. The rewritten integral will be dx = 15 sec θ tan θ dθ / (225 + 225 sec² θ)².
In trigonometric substitution, we choose a substitution that simplifies the integral by transforming it into a form that can be easily evaluated using trigonometric identities. In this case, the most helpful substitution is x = 15 sec θ.
To rewrite the integral, we need to express dx in terms of θ. Since x = 15 sec θ, we can differentiate both sides with respect to θ to find dx. The derivative of sec θ is sec θ tan θ, so we have dx = 15 sec θ tan θ dθ.
Substituting this expression for dx and rewriting (225 + x²)² in terms of θ, we obtain:
∫(x² dx) / (225 + x²)² = ∫[(15 sec θ)² (15 sec θ tan θ dθ)] / (225 + (15 sec θ)²)².
Simplifying further, we get:
∫(225 sec² θ tan θ dθ) / (225 + 225 sec² θ)².
This is the rewritten form of the integral using the substitution x = 15 sec θ.
Learn more about trigonometric substitution here:
https://brainly.com/question/32150762
#SPJ11
Hi My teacher hasn't been in online class for a week and I dont get the math and I need help

Answers
Sebastian, this is the solution to the first problem you uploaded:
Let's recall that the interior angles of a triangle add up to 180 degrees.
Then if E =