A table is made using the following two patterns.
Pattern x: Starting number: 1, Rule: add 1
Pattern y: Starting number: 5, Rule: add 5
Complete the table for the given patterns.
x y
1 5
Answers
Answer:
The required table will be
x y
1 5
2 10
3 15
4 20
5 25
Step-by-step explanation:
We are given 2 patterns
Pattern x: Starting number: 1, Rule: add 1
Pattern y: Starting number: 5, Rule: add 5
We need to complete the table for given patterns
x y
1 5
The second number for x according to pattern will be: we will add 1 to the previous number i.e 1+1 =2
The third number for x according to pattern will be: we will add 1 to the previous number i.e 2+1 =3
The second number for y according to pattern will be: we will add 5 to the previous number i.e 5+5 =10
The third number for y according to pattern will be: we will add 5 to the previous number i.e 10+5 =15
So, the required table will be
x y
1 5
2 10
3 15
4 20
5 25
As we are not given how much we need to fill table. I am adding 4 values for x and y.
Related Questions
The paved area is a square with sides 2 m long.
The paving stones for this area are squares that measure 50 cm by 50 cm
How many paving stones are needed?
Answers
Answer:
Step-by-step explanation:
2 meters = 200 cm
200 cm × (1 block)/(50 cm) = 4 blocks
4 blocks by 4 blocks = 16 blocks
Answer:
16 paving stones
Step-by-step explanation:
1 m = 100 cm
The square has sides 200 cm long
Its area is 200(200) = 40000 sq cm
Each paving stone has an area of 50(50) = 2500 sq cm
So 40000/2500 = 16 paving stones
A group of students go out on a boat to go scuba diving. The instructor takes the group 57.52 feet below the surface to start. Then they go up 24.88 feet and stop to see some fish. Estimate the total change in distance from where they started at the surface. Find the total change in distance from where they started at the surface..
Answers
Answer:
it is 82.13
Step-by-step explanation:
you can add the 57.52+24.88
HELP PLEASE
Solve the right triangle if the hypotenuse is 5 and one acute angle is 34°. Round answers to two decimal places.

Answers
i. α = 56°
ii. adj = 4.1
iii. opp = 2.79
What is the right angle triangle?We have to recall that what makes the right angle triangle unique is the fact that one of the angles that we find in the triangle is 90 degrees. We have to recall that the sum of the angles that we have in a triangle is 180°.
Hence we have;
α = 180 - (90 + 34)
α = 56°
Then;
Cos 34 = adj/5
adj = 5 cos 34
= 4.1
Sin 34 = opp/5
opp = 5 * sin 34
= 2.79
These are the parts of the right angled triangle required.
Learn more about triangle:https://brainly.com/question/2773823
#SPJ1
What is the volume of the cylinder below?

Answers
Answer:
The volume of the cylinder is \(112\ \text{units}^3\).
Step-by-step explanation:
We have,
Radius of the cylinder is 4 units
Height of the cylinder is 7 units
It is required to find the volume of the cylinder. The formula of the volume of the cylinder is given by :
\(V=\pi r^2 h\)
Plugging all the values, we get :
\(V=\pi \times (4)^2\times 7\\\\V=112\ \text{units}^3\)
So, the volume of the cylinder is \(112\ \text{units}^3\). The correct option is (b).
Find the slope of a line perpendicular to the line whose equation is x + 6y = -24.
Fully simplify your answer.
Answers
Answer:
\(m_{perpendicular}\) = 6
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
given
x + 6y = - 24 ( subtract x from both sides )
6y = - x - 24 ( divide through by 6 )
y = - \(\frac{1}{6}\) x - 4 ← in slope- intercept form
with slope m = - \(\frac{1}{6}\)
given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{-\frac{1}{6} }\) = 6
A tire swing hangs straight down. Then a child gets on, swings forward 50°, and swings back 95°. How many degrees forward must the swing go to return to its starting position?
Answers
Let's draw a picture of the problem:
From the picture above, we can see that the difference (x) between the second and third position is
\(95-50=x\)which gives
\(x=45\)How many degrees forward must the swing go to return to its starting position? Answer: 45 degrees forward

Please help I can’t figure it out

Answers
well, let's first off find out how many actually do favor it in the first place.
\(\stackrel{total}{4000}\cdot \cfrac{3}{8}\implies \stackrel{seniors}{\text{\LARGE 1500}}\hspace{12em}\stackrel{total}{4000}-1500=\stackrel{not~seniors}{\text{\LARGE 2500}} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{seniors}{\text{\LARGE 1500}}\cdot \cfrac{1}{6}\implies \stackrel{in~favor}{\text{\LARGE 250}}\hspace{11em} \stackrel{not~seniors}{\text{\LARGE 2500}}\cdot \cfrac{3}{5}\implies \stackrel{in~favor}{\text{\LARGE 1500}} \\\\[-0.35em] ~\dotfill\\\\ 250+1500\implies \stackrel{in~favor}{\text{\LARGE 1750}}\hspace{15em}\boxed{\underset{\textit{do not favor it}}{\stackrel{4000~~ - ~~1750}{\text{\LARGE 2250}}}}\)
What is the present value of R13 000 p.a. invested at the beginning of each year for 8years at 10%p.a. compound interest? (NB Use the compound interest tables provided or work to three decimal places only.)
Answers
Given statement solution is :- The present value of R13,000 per year invested for 8 years at 10% compound interest is approximately R69,776.60.
To calculate the present value of an investment with compound interest, we can use the formula for the present value of an annuity:
PV = A *\((1 - (1 + r)^(-n)) / r\)
Where:
PV = Present value
A = Annual payment or cash flow
r = Interest rate per period
n = Number of periods
In this case, the annual payment (A) is R13,000, the interest rate (r) is 10% per year, and the investment is made for 8 years (n).
Using the formula and substituting the given values, we can calculate the present value:
PV = \(13000 * (1 - (1 + 0.10)^(-8)) / 0.10\)
Calculating this expression:
PV = \(13000 * (1 - 1.10^(-8)) / 0.10\)
= 13000 * (1 - 0.46318) / 0.10
= 13000 * 0.53682 / 0.10
= 6977.66 / 0.10
= 69776.6
Therefore, the present value of R13,000 per year invested for 8 years at 10% compound interest is approximately R69,776.60.
For such more questions on present value
https://brainly.com/question/30390056
#SPJ8
A rectangle has an area of 36 mm2. All of the sides
are the same length.
What is the length of a single side?
Answers
Answer:
6mm
Step-by-step explanation:
A rectangle with all sides equal is a square
Area=a
36=a
a=6mm
Express in simplest radical form.
V9
Answers
Answer:
3
Step-by-step explanation:
\(\sqrt{9}=\sqrt{3*3} = 3\)
What key features do the functions f(x) = 4-x and g of x equals negative one times the square root of the x minus 4 end root have in common? Both f(x) and g(x) include domain values of [–4, ∞) and range values of (–∞, ∞), and both functions have an x-intercept in common. Both f(x) and g(x) include domain values of [4, ∞), and both functions decrease over the interval (4, ∞). Both f(x) and g(x) include domain values of [4, ∞) and range values of [0, ∞), and both functions have a y-intercept in common. Both f(x) and g(x) include domain values of [–4, ∞) and range values of (–∞, ∞), and both functions are negative for the entire domain.
Answers
The statement about both functions that is true is:
Both f(x) and g(x) include domain values of [4, ∞), and both functions decrease over the interval (4, ∞). What is the domain and range for the function of y = f(x)?The domain of a function is the set of values of input for which the function is valid.
The range is the dependent variable of a set of values for which the function is defined.
Given that:
f(x) = 4 - x
The slope (m) of the function = -1x-intercept = (4,0)y-intercept = (0,4)Domain = [4,∞)For function g(x) = -1 ×\(\mathbf{\sqrt{x-4}}\)
The domain = x ≥ 4 and the solution set is [4,∞)The range g(x) = ≤ 0 and the solution set is [-∞, 0)The function g(x) does not have a y-intercept.Therefore, from the given options, the statement about both functions that is true is:
Both f(x) and g(x) include domain values of [4, ∞), and both functions decrease over the interval (4, ∞).Learn more about the domain of a function here:
https://brainly.com/question/1369616
#SPJ1
Answer:
Both f(x) and g(x) include domain values of [4, ∞), and both functions decrease over the interval (4, ∞).
Step-by-step explanation:
I got it right on the test.
There are 60 children in a club.
In the club, the ratio of the number of girls to the number of boys is 3:1
3/5 of the girls play a musical instrument.
4/5 of the boys play a musical instrument.
What fraction of the 60 children play a musical instrument?
(4 marks)
Answers
What is the equation of the line that passes through the point (7,6) and has a slope of 0
Answers
The equation of the line that passes through the point (7, 6) with slope 0 is y = 6
Given,
The points which the line passes, (x₁, y₁) = (7, 6)
Slope of the line, m = 0
We have to find the equation of the line:
We know that,
y - y₁ = m(x - x₁)
So,
y - 6 = 0(x - 7)
y - 6 = 0
y = 6
That is,
The equation of the line that passes through the point (7, 6) with slope 0 is y = 6
Learn more about equation of line here:
https://brainly.com/question/25789778
#SPJ1
PLEASE HELP ME
The function f(x) = -2(4)^x+1 +140
represents the number of tokens a child has x hours after arriving at an arcade.
What is the practical domain and range of the function?
If necessary, round to the nearest hundredth.
The practical domain of the situation is ?
The practical range of the situation is ?
PLEASE SEE PHOTO FOR FUNCTION

Answers
The function f(x) = -2(4)ˣ⁺¹ +140 represents the number of tokens a child has x hours after arriving at an arcade. The practical domain and range of the function are x ≥ 0 and The practical range of the situation is [140, ∞).
The given function is f(x) = -2(4)ˣ⁺¹+ 140, which represents the number of tokens a child has x hours after arriving at an arcade.
To determine the practical domain and range of the function, we need to consider the constraints and limitations of the situation.
For the practical domain, we need to identify the valid values for x, which in this case represents the number of hours the child has been at the arcade. Since time cannot be negative in this context, the practical domain is x ≥ 0, meaning x is a non-negative number or zero.
Therefore, the practical domain of the situation is x ≥ 0.
For the practical range, we need to determine the possible values for the number of tokens the child can have. Looking at the given function, we can see that the term -2(4)ˣ⁺¹represents a decreasing exponential function as x increases. The constant term +140 is added to shift the graph upward.
Since the exponential term decreases as x increases, the function will have a maximum value at x = 0 and approach negative infinity as x approaches infinity. However, due to the presence of the +140 term, the actual range will be shifted upward by 140 units.
Therefore, the practical range of the situation will be all real numbers greater than or equal to 140. In interval notation, we can express it as [140, ∞).
To summarize:
- The practical domain of the situation is x ≥ 0.
- The practical range of the situation is [140, ∞).
Know more about the domain here:
https://brainly.com/question/30096754
#SPJ8
which expressions are equivalent to 3^4/9/3^2/9? select all that apply

Answers
Answer:
first and third expressions
Step-by-step explanation:
using the rule of exponents
\(\frac{a^{m} }{a^{n} }\) = \(a^{m-n}\)
then
\(\frac{3^{\frac{4}{9} } }{3^{\frac{2}{9} } }\)
= \(3^{\frac{4}{9}-\frac{2}{9} }\) ← first expression
= \(3^{\frac{2}{9} }\) ← third expression
Can you guys help me with this please

Answers
Step-by-step explanation:
Using rules of logs :
9 loga x = loga x^9
Then using another rule:
loga x^9 + loga y = loga (x^9 * y )
Express the sum of the angles of this triangle in two different ways.
X
1/2x
3/2x
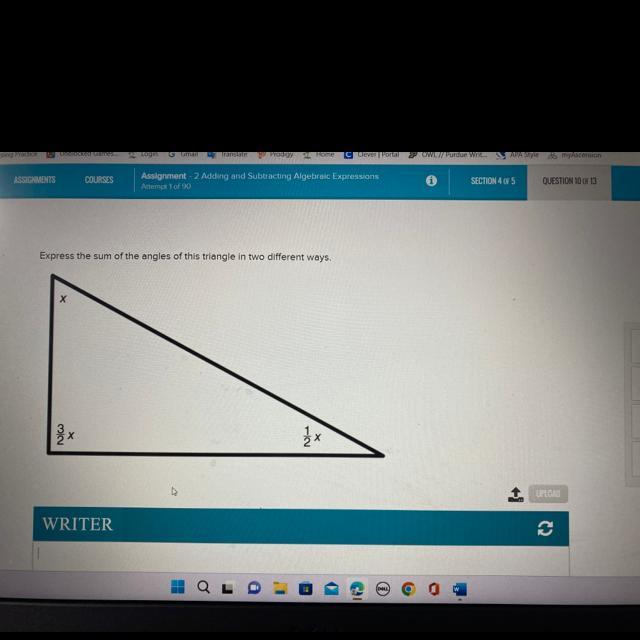
Answers
The sum of the angles of the triangle expressed in two ways are x + 1/2x + 3/2x and 2x + x + 3x/2
How to determine the expressionIt is important to note that the sum of the angles of a triangle is equal or equivalent to 180 degrees.
We have the angle measurements as;
x3/2x1/2xSubstitute the values
x + 1/2 x + 3/2x = 180
Find the lowest common multiple
2x + x + 3x /2 = 180
Add the numerators
6x/2 = 180
cross multiply
6x = 360
x = 60
Hence, the expression is x + 1/2x + 3/2x and 2x + x + 3x/2
Learn more about triangles here:
https://brainly.com/question/14285697
#SPJ1
sarah ran 20 miles over 5 days how many miles did she run every day
Answers
Answer:
that's easy she ran 4 every day
Step-by-step explanation:
4x5 equals 20 for the first day she ran 4 second day 8 third 12 fourth 16 fifth 20
What’s the correct answer for this?

Answers
Answer:
Answer is the first one :)
Step-by-step explanation:
√(-7-5)² + (-7-9)²
answer is 20
hope this helps
Answer:
A.
Step-by-step explanation:
In the attached file

x/9=7/15 answer plss
Answers
Answer: To solve for x in the equation x/9 = 7/15, we can cross-multiply to get:
15x = 9 * 7
Simplifying the right side, we get:
15x = 63
To solve for x, we can divide both sides by 15:
x = 63/15
Simplifying the fraction on the right side, we get:
x = 4 3/5 or x = 4.2 (rounded to one decimal place)
Therefore, the solution to the equation x/9 = 7/15 is x = 4.2 or x = 4 3/5.
Step-by-step explanation: kinda easy ngl lol but hope this helps :D
Find two integers whose sum is 11 and whose product is 30.

Answers
5 x 6 = 30
The following table shows the times of trains between Juno and Odiham.
Station
Times
Station
Times
Juno
07:15
22:15
Odiham
07:00
22:00
Kepler
07:24
and every
22:24
Ninar
07:10
and every
22:10
Lemma
07:32
20 minutes 22:32
Morgan
07:25
20 minutes 22:25
07:40
until
22:40
Lemma
07:33
until
22:33
Morgan
Ninar
07:55
22:55
Kepler
07:41
22:41
Odiham
08:05
23:05
Juno
07:50
22:50
Ferdo lives in Juno. He has a business appointment in Odiham and needs to be there for at least
two hours between his arrival in and departure from Odiham. He leaves Juno on the first train after
08:30.
(a) What is the earliest time that Ferdo can be back at Juno station after his appointment?
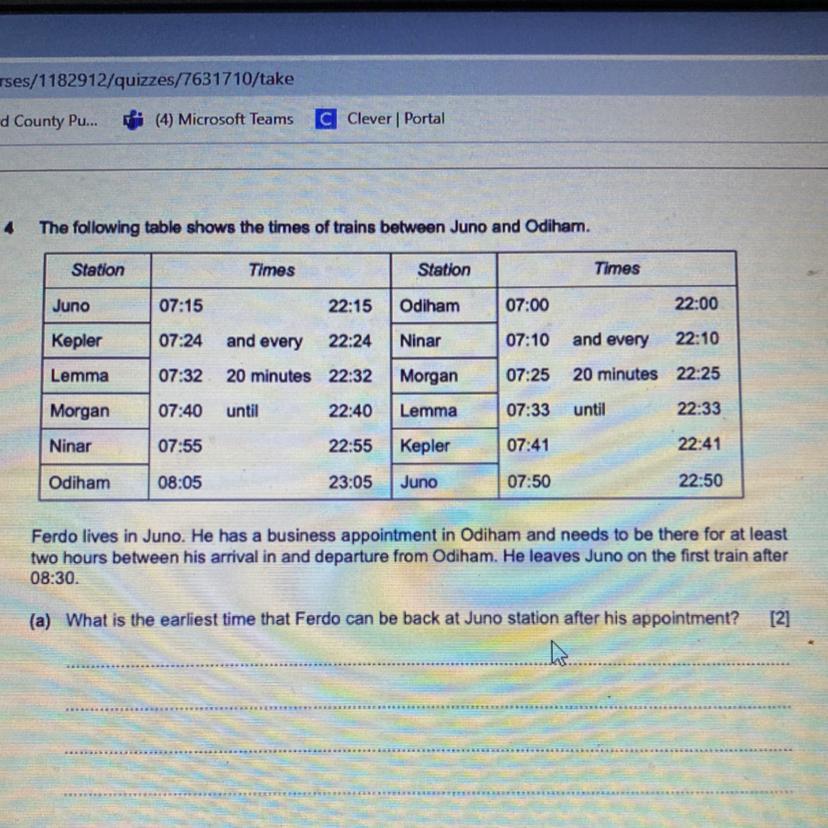
Answers
Answer:
(a) The earliest time that Ferdo can be back at Juno station is 12:15
Step-by-step explanation:
From the given table, we have;
The starting time for train departure from Juno = 07:15
The frequency of train departures from Juno = Every 20 minutes
The time of departure, 't₁' of first train that departs from Juno after 08:30 is given as follows;
The train departure times from Juno = 07:15, 07:35, 07:55, 08:15, 08:35
Therefore;
The time at which the first train departs from Juno after 08:30 = 08:35
The time it takes a train to travel from Juno to Odiham = 0:805 - 07:15 = 50 minutes
The time of arrival of the train Ferdo takes from Juno at Odiham = 08:35 + 50 minutes = 09:25
The number of hours Ferdo spends at Odiham = 2 hours
The time after which Ferdo departs from Odiham = 09:25 + 02:00 = 11:25
The time of departure of the train from Odiham after 11:25 = 08:05 + 20 minutes × 10
Therefore, the time of departure of the train from Odiham after = 11:25
The time it takes on the trip back to Juno from Odiham = 50 minutes
The earliest time that Ferdo can be back at Juno station = 11:25 + 50 minutes = 12:15
Find the measure of the missing angles.

Answers
Answer:
Step-by-step explanation:
e = 61°, f = 119°, and d = 90°
We know that vertically opposite angles are equal.
So, e = 61° [Vertically opposite angles]
We know that linear pair of angles are supplementary (180°).
So, f + 61° = 180° [Linear pair of angles]
=> f = 180° - 61°
=> f = 119°
and d + 90° = 180° [Linear pair of angles]
=> d = 180° - 90°
=> d = 90°
: Find the equation of the tangent line to the curve f(x)= e^xat x_0= 2, and show this line on the graph.
Answers
The tangent line to f(x) = e ˣ at the point x = 2 has slope equal to f ' (2):
f(x) = e ˣ → f '(x) = e ˣ → f ' (2) = e ²
At x = 2, the function takes on a value of f (2) = e ². Use the point-slope formula to get the equation of the tangent line:
y - e ² = e ² (x - 2)
Solve for y :
y = e ² x - e ²
answer the number 2 only

Answers
The missing variables on item 2 are given as follows:
\(o = 12\sqrt{3}\)i = 24.What are the trigonometric ratios?The three trigonometric ratios are the sine, the cosine and the tangent of an angle, and they are obtained according to the formulas presented as follows:
Sine = length of opposite side to the angle/length of hypotenuse of the triangle.Cosine = length of adjacent side to the angle/length of hypotenuse of the triangle.Tangent = length of opposite side to the angle/length of adjacent side to the angle = sine/cosine.For the angle of 60º, we have that:
o is the opposite side.12 is the adjacent side.Hence the length o is given as follows:
tan(60º) = o/12.
\(\sqrt{3} = \frac{o}{12}\)
\(o = 12\sqrt{3}\)
Applying the Pythagorean Theorem, the length i is given as follows:
i² = 12² + \((12\sqrt{3})^2\)
i² = 576
i² = 24²
i = 24.
A similar problem, also about trigonometric ratios, is given at brainly.com/question/24349828
#SPJ1
Answer:
o = 12√3
i = 24
Step-by-step explanation:
From observation of the given right triangle, we can see that two of its interior angles measure 60° and 90°. As the interior angles of a triangle sum to 180°, this means that the remaining interior angle must be 30°, since 30° + 60° + 90° = 180°. Therefore, the triangle is a special 30-60-90 triangle.
The side lengths in a 30-60-90 triangle have a special relationship, which can be represented by the ratio formula a : a√3 : 2a, where "a" represents a scaling factor that can be any positive real number.
Side a is opposite the 30° angle (shortest leg).Side a√3 is opposite the 60° angle (longest leg).Side 2a is the hypotenuse (longest side).In triangle #2, the shortest leg is 12 units.
As "a" is the shortest leg, the scale factor "a" is 12.
The side labelled "o" is the longest leg opposite the 60° angle. Therefore:
\(o = a\sqrt{3}=12\sqrt{3}\)
The side labelled "i" is the hypotenuse of the triangle. Therefore:
\(i= 2a = 2 \cdot 12=24\)
Therefore:
o = 12√3i = 24Pankaj is a Biomedical Engineering student. He plans to deposit $600 that he earned as stipend, in
a bank account at 3% rate of interest compounded weekly for no more than 2 years. The total
amount of the money, A, that Pankaj will get back, is a function of time, t. Which is a reasonable
domain of the money that he may accumulate?

Answers
The correct answer is A: 600 <= money <= 2822.4.
This represents the range of possible values that Pankaj's accumulated money could fall into, given the specified conditions of the 3% interest rate compounded weekly for a maximum of 2 years. The lower bound, 600, represents the initial deposit amount, while the upper bound, 2822.4, represents the maximum amount of money Pankaj could earn after 2 years, assuming that interest is compounded every week.
please help i am giving away brainliest
A swimming pool in the shape of a cylinder with a diameter of 10 m and a depth of 3 m is being filled with water. 27,535 L have been added so far. 1 m3 is equal to 1000 L. To the nearest liter, how much more water can the pool hold?
A. 236,000 L
B. 208,084 L
C. 236,616 L
D. 207,314 L
No dam links
Answers
Answer:
207,314
Step-by-step explanation:
V = πr2h =π · 52·3 ≈ 235.61945 m^3
because 1m^3 = 1000 L, (27,535 / 1000) = the amount of added water in m^3. As this is equal to 27.535, we can substract this from 235.62.
235.62 - 27.535 is about 208.085, or 207.314 because of rounding. As this is in m^3, we multiply by liters to arrive at the answer of 207,314, or option D.
Two is subtracted from a number, and then the difference is divided by 3. The result is 30. Find the number.
Answers
Hey there! I'm happy to help!
Let's call this number n. Here is the equation we can write.
(n-2)/3=30
We multiply both sides by 3.
n-2=90
We add 2 to both sides.
n=92.
Have a wonderful day! :D
Two rectangular picture frames have the same area of 45 square inches but have different side lengths. Frame A has a length of 6 3/4 inches, and Frame B has a length of 7 1/2 inches.
Without calculating, predict which frame has the shorter width. Explain your reasoning.
Find the width that you predicted to be shorter.
Answers
Answer:
B, 6 inches
Step-by-step explanation:
The formula for area is width * height. If the area is the same in both times, increasing height means you must be decreasing width. B has a taller height so must have a shorter width.
7 and 1/2 = 15/2
45 / (15 / 2) = 45 * 2 / 15 = 6 inches
A bucket contains 72 red, 48 blue, 48 green, and 48 yellow crayons. The art teacher also has 120 pieces of drawing paper. What is the largest number of identical kits the art teacher can make with all of the crayons and all of the paper?
Answers
The art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper for proper distribution.
To determine the largest number of identical kits the art teacher can make using all the crayons and drawing paper, we need to find the greatest common divisor (GCD) of the quantities.
The GCD represents the largest number that can divide all the quantities without leaving a remainder.
The GCD of the quantities of crayons can be found by considering the prime factorization:
72 = 2³ × 3²
48 = 2⁴ × 3
48 = 2⁴ × 3
48 = 2⁴ × 3
The GCD of the crayons is 2³ × 3 , which is 24.
Now, we need to find the GCD of the quantity of drawing paper:
120 = 2³ × 3 × 5
The GCD of the drawing paper is also 2³ × 3 , which is 24.
Since the GCD of both the crayons and drawing paper is 24, the art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper.
Each kit would contain an equal distribution of crayons and drawing paper.
Learn more about distribution here:
brainly.com/question/30034780
#SPJ1