a tax rate of $.0711 in decimal expressed per $1,000 of assessed valuation is equal to:
Answers
A tax rate of $0.0711 per $1,000 of assessed valuation in decimal form can be calculated as follows. First, divide the tax rate by 1,000 to determine the rate per dollar: $0.0711 / 1,000 = $0.0000711.
This represents the decimal equivalent of the tax rate per dollar. To express it as a percentage, multiply the decimal value by 100: $0.0000711 * 100 = 0.00711%.
Therefore, a tax rate of $0.0711 per $1,000 of assessed valuation is equal to 0.00711% in decimal form.
To know more about tax rate, visit:
https://brainly.com/question/30629449
#SPJ11
Related Questions
Which expression is a factor of x² + 3x - 40?
A. (x-4)
B. (x - 5)
C. (x-8)
D. (x-10)
Answers
The result is not equal to zero, (x - 10) is not a factor of x² + 3x - 40.
None of the given expressions (A, B, C, D) are factors of x² + 3x - 40.
To determine which expression is a factor of the given quadratic expression, we need to check if substituting the value from each expression into the quadratic expression results in zero. Let's evaluate each option:
A. (x - 4)
Substituting x - 4 into x² + 3x - 40:
(x - 4)² + 3(x - 4) - 40 = x² - 8x + 16 + 3x - 12 - 40 = x² - 5x - 36
Since the result is not equal to zero, (x - 4) is not a factor of x² + 3x - 40.
B. (x - 5)
Substituting x - 5 into x² + 3x - 40:
(x - 5)² + 3(x - 5) - 40 = x² - 10x + 25 + 3x - 15 - 40 = x² - 7x - 30
Since the result is not equal to zero, (x - 5) is not a factor of x² + 3x - 40.
C. (x - 8)
Substituting x - 8 into x² + 3x - 40:
(x - 8)² + 3(x - 8) - 40 = x² - 16x + 64 + 3x - 24 - 40 = x² - 13x
Since the result is not equal to zero, (x - 8) is not a factor of x² + 3x - 40.
D. (x - 10)
Substituting x - 10 into x² + 3x - 40:
(x - 10)² + 3(x - 10) - 40 = x² - 20x + 100 + 3x - 30 - 40 = x² - 17x + 30
Since the result is not equal to zero, (x - 10) is not a factor of x² + 3x - 40.
None of the given expressions (A, B, C, D) are factors of x² + 3x - 40.
For more such questions on factor , Visit:
https://brainly.com/question/25829061
#SPJ11
The intersection of two mutually exclusive events: A. can be any value between 0 and 1 B. must always be equal to 1 C. must always be equal to 0 D. can be any positive value If A and B are independent events with P(A) = 0.4 and P(B) =0.6, then P(A B) = A. 0.76 B. 1.00 C. 0.24 D. 0.20 If A and B are independent events with P(A) = 0.05 and P(B) =0.65, then P(A / B) = A. 0.05 B. 0.65 C. 0.8 D. 0.0325
Answers
If A and B are independent events with given probabilities P(A) and P(B), then the probability of A intersecting B (P(A ∩ B)) is equal to the product of their individual probabilities. For example, if P(A) = 0.05 and P(B) = 0.65, then P(A ∩ B) = 0.0325.
The probability of two events A and B occurring together, P(A ∩ B), can be calculated by multiplying the individual probabilities of each event, P(A) and P(B). In this case,
P(A) = 0.4 and P(B) = 0.6, so P(A ∩ B) = 0.4 * 0.6 = 0.24
.The probability of event A occurring given that event B has already occurred, P(A | B), is equal to the probability of both events occurring together, P(A ∩ B), divided by the probability of event B occurring, P(B). In this case,
P(A ∩ B) = 0.24 and P(B) = 0.65, so P(A | B) = 0.24 / 0.65 = 0.0375
which can be rounded to 0.0325.These probabilities can be used to estimate the likelihood of certain events occurring together or given certain conditions. In this case, the probability of events A and B occurring together is 0.24 and the probability of event A occurring given that event B has already occurred is 0.0325.
A. P(A ∩ B) = P(A) * P(B)
= 0.4 * 0.6
= 0.24
B. P(A | B) = P(A ∩ B) / P(B)
= 0.24 / 0.65
= 0.0375
= 0.0325
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
A company that makes robotic vacuums claims their newest model of vacuum lasts, on average, two hours when starting on a full charge. To investigate this claim, a consumer group purchases a random sample of five vacuums of this model. They charge each unit fully and then measure the amount of time each unit runs. Here are the data (in hours): 2.2, 1.85, 2.15, 1.95, and 1.90. They would like to know if the data provide convincing evidence that the true mean run time differs from two hours. What are the appropriate hypotheses?
H0: μ = 2 versus Ha: μ < 2, where μ = the true mean run time for all vacuums of this model
H0: μ = 2 versus Ha: μ > 2, where μ = the true mean run time for all vacuums of this model
H0: μ = 2 versus Ha: μ ≠ 2, where μ = the true mean run time for all vacuums of this model
H0: μ ≠ 2 versus Ha: μ = 2, where μ = the true mean run time for all vacuums of this model
Answers
Answer:
The answer is C. H0: μ = 2 versus Ha: μ ≠ 2, where μ = the true mean run time for all vacuums of this model
Step-by-step explanation:
EDGE 2021
what is the sum 28 sigma i=1 (8i-13)
Answers
The sum of the expression 28 ∑_{i=1} (8i - 13) is 11171.
To find the sum of the expression 28 ∑_{i=1} (8i - 13), we need to evaluate the expression for each value of i from 1 to 28 and then add up the results.
Let's break down the expression 8i - 13 for i = 1 to 28:
For i = 1: 8(1) - 13 = 8 - 13 = -5
For i = 2: 8(2) - 13 = 16 - 13 = 3
For i = 3: 8(3) - 13 = 24 - 13 = 11
...
For i = 28: 8(28) - 13 = 224 - 13 = 211
Now, we can add up all these individual values:
(-5) + 3 + 11 + ... + 211
To simplify the calculation, we can use the formula for the sum of an arithmetic series:
Sum = (n/2)(first term + last term)
In this case, the first term is -5 and the last term is 211. The number of terms, n, can be determined by subtracting the first term from the last term and then adding 1:
n = last term - first term + 1
n = 211 - (-5) + 1
n = 211 + 5 + 1
n = 217
Substituting these values into the sum formula, we get:
Sum = (217/2)(-5 + 211)
Sum = (217/2)(206)
Sum = 11171
Learn more about arithmetic series at: brainly.com/question/14203928
#SPJ11
Please help will mark brainliest if correct

Answers
Answer:
Step-by-step explanation:
Triangles are congruent by SAS postulate.
The surface area of a sphere is 314 square meters. Which equation can be used to find the radius of the sphere?
Recall the formula S A = 4 pi r squared.
314 = 4 pi r
314 = 4 pi r squared
314 = (4 pi r) squared
314 = 4 pi r squared + 2 pi r
Answers
Answer:
314 =4 Pi (r squrared)
Step-by-step explanation:
so second option is the right answer
Is 210879 divisible by 3?
PLEASE HELPP
Answers
Answer:
Yes
Step-by-step explanation:
Well to figure out if 210879 is divisible by 3 we do,
210879 / 3
= 70 293.
Thus,
210879 is divisible by 3.
Hope this helps :)
Answer: Yes
Explanation: To determine whether 210,879 is divisible by 3, first we need to find the sum of the digits.
Image is provided below.
The divisibility rules tell us that if the sum of the digits is divisible by 3,
then the number is also divisible by 3.
So since 27 is divisible by 3, 210,879 must also divisible by 3.
So our answer is yes, 210,879 is divisible by 3.
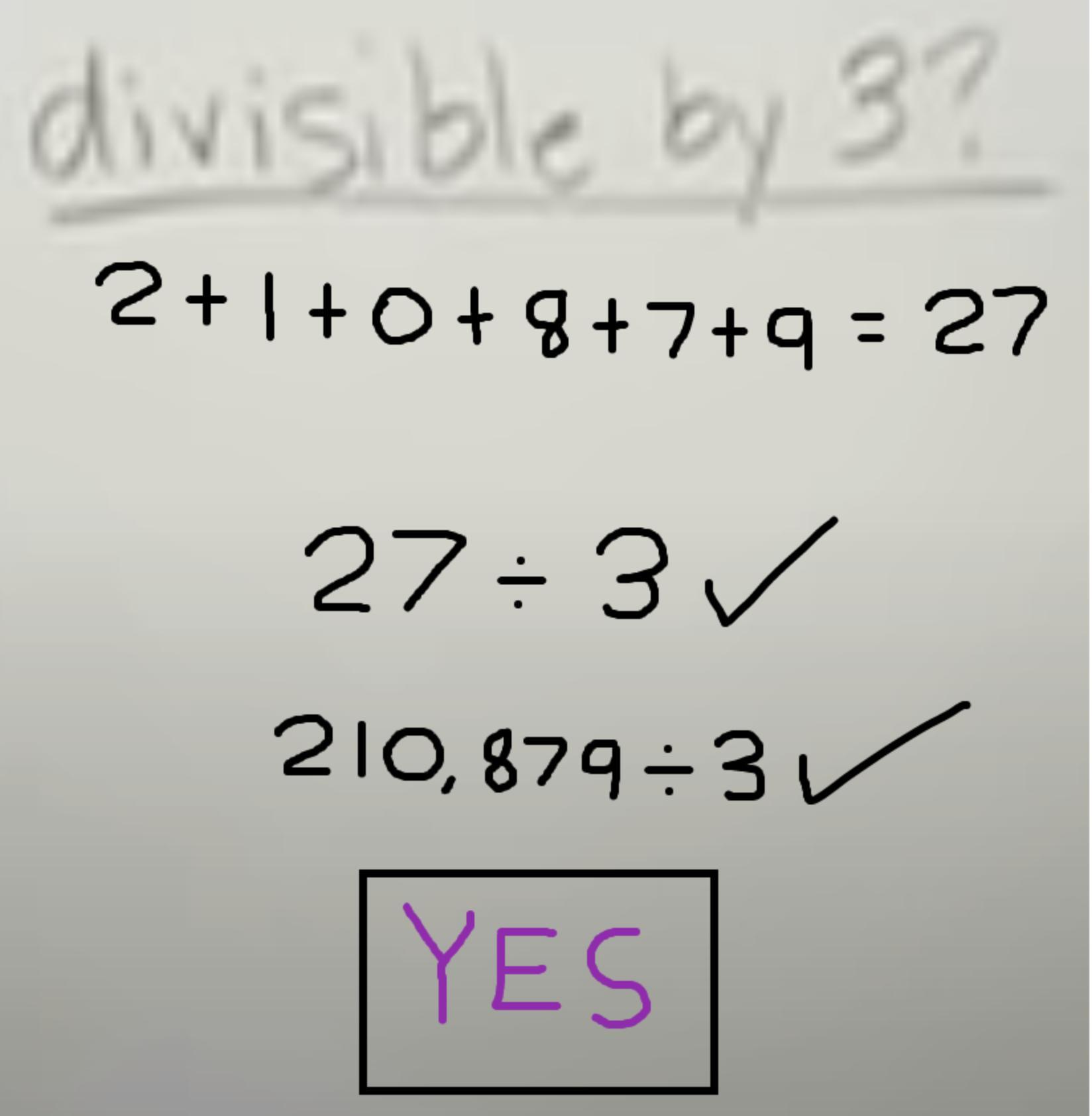
discrete mathematics and its applications answers to even numbered exercises 8th edition
Answers
The statement “The sum of two odd integers is odd” is true because if both integers are odd, the sum will be an odd integer.
1. Answer: False
2. Answer: True
3. Answer: False
4. Answer: True
5. Answer: False
6. Answer: True
7. Answer: False
8. Answer: True
9. Answer: False
10. Answer: True
1. False: The statement “Every odd integer is prime” is false because some odd integers are not prime, e.g. 9.
2. True: The statement “The square of an even integer is even” is true because the square of any even integer can be written as 2k for some integer k, and 2k is even.
3. False: The statement “The sum of two odd integers is even” is false because if both integers are odd, the sum will be an odd integer.
4. True: The statement “The product of two even integers is even” is true because the product of two even integers can be written as 4k for some integer k, and 4k is even.
5. False: The statement “Every even integer is divisible by 4” is false because some even integers are not divisible by 4, e.g. 6.
6. True: The statement “The sum of two even integers is even” is true because the sum of two even integers can be written as 2k for some integer k, and 2k is even.
7. False: The statement “The product of two odd integers is even” is false because the product of two odd integers is an odd integer.
8. True: The statement “The square of an odd integer is odd” is true because the square of any odd integer can be written as 2k + 1 for some integer k, and 2k + 1 is odd.
9. False: The statement “Every even integer is divisible by 8” is false because some even integers are not divisible by 8, e.g. 14.
10. True: The statement “The sum of two odd integers is odd” is true because if both integers are odd, the sum will be an odd integer.
The complete question is :
Q. Are the following statements true or false?
1. Every odd integer is prime.
2. The square of an even integer is even.
3. The sum of two odd integers is even.
4. The product of two even integers is even.
5. Every even integer is divisible by 4.
6. The sum of two even integers is even.
7. The product of two odd integers is even.
8. The square of an odd integer is odd.
9. Every even integer is divisible by 8.
10. The sum of two odd integers is odd.
Learn more about integer here
https://brainly.com/question/15276410
#SPJ4
what is x+y=6???? i need help asap and u will mark brainliest!!!
Answers
Answer:
0,6 6,0
Step-by-step explanation:
but hey use DESMOsS.COmM its super useful
Answer:
Step-by-step explanation:
there are a couple ansers
3+3=6
4+2=6
5+1=6
6+0=6
Reflect (1, -4) over the x-axis.
Then translate the result up 3 units.
What are the coordinates of the final point?
Answers
Answer: (4,4)
Step-by-step explanation:
(1,-4) reflected over the x-axis is (1,4). Then translated 3 units up is (4,4). Hope this helps
The mean length of 6 rods is 44.2 cm. The mean length of 5 of them is 46 cm. How long is the sixth rod?
Answers
Answer:
The sixth rod is 35.20 cm.
Step-by-step explanation:
Get the total length of the 6 rods.
Total length = 6(44.2cm)
= 265.20 cm
Get the total length of 5 rods
Length of 5 rods = 5(46cm)
=230cm
The length of the sixth rod is the difference between the two.
Length of the sixth rod = 265.20 cm - 230 cm
length = 35.2 cm
7 Find in degrees. 19 0 [?] degrees Round to the nearest hundredth.
![7 Find in degrees. 19 0 [?] degrees Round to the nearest hundredth.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/NBf7Hy68pBia2eoLhai0bjxjmEexy8UY.jpeg)
Answers
Answer:
Θ ≈ 21.62°
Step-by-step explanation:
using the sine ratio in the right triangle
sinΘ = \(\frac{opposite}{hypotenuse}\) = \(\frac{7}{19}\) , then
Θ = \(sin^{-1}\) ( \(\frac{7}{19}\) ) ≈ 21.62° ( to the nearest hundredth )
I will award Brainleist if you answer ASAP
The area of a rectangle is represented by the function x^3 − 2x^2 − 40x − 64.
The width of the rectangle is x + 4. Find the expression representing the length of the rectangle.
x^2 − 8x − 20
x^2 + 12x + 20
x^2 − 6x − 16
x^2 + 10x + 16
Answers
The length of the rectangle is represented by the expression x^2 − 6x − 16. (option c)
To find the expression representing the length, we need to use the fact that the area of a rectangle is given by the product of its length and width. In this case, the area of the rectangle is given by the function x^3 − 2x^2 − 40x − 64. Since the width of the rectangle is x + 4, we can write the area as
(x + 4) * L
where L is the length of the rectangle.
To find the expression for L, we can set
x^3 − 2x^2 − 40x − 64 = (x + 4) * L and solve for L.
First, we distribute the x + 4 on the right side of the equation:
x^3 − 2x^2 − 40x − 64 = x^2 * L + 4L. Then, we compare the coefficients of the x^2 and x terms on both sides of the equation: -2 = L + 4L, which simplifies to -2 = 5L. Finally, we solve for L: L = -2/5.
Thus, the expression representing the length of the rectangle is -2/5.
Learn more about rectangle :
https://brainly.com/question/25292087
#SPJ4
Solve the equation.
-9x + 1 = -x + 17
X=-8
O X=-2
X = 2
X = 8
Answers
Answer:
-9x + x = 17 – 1
8x = 16
X = 16/8
X=2
determine whether the series is absolutely convergent, conditionally convergent, or divergent. sum_(n=0)^infinity (-14)^n/n!
Answers
Answer:
Absolutely Convergent
yw;)
Step-by-step explanation:
To determine whether the series is absolutely convergent, we can consider the absolute value of its terms: |(-14)^n/n!| = 14^n/n!. This is the Taylor series expansion for e^(14), which also converges. Therefore, the original series is absolutely convergent.
Find the magnitude of vector v given that its component form is = (5,–12).
Answers
The magnitude of vector v given that its component form is ( 5,–12 ) is 13 .
The magnitude (or length) of a vector with components (a, b) is given by the formula
Magnitude = √(a² + b²).
In this case, vector v has components ( 5, -12 ).
a = 5 , b = -12
Let's calculate its magnitude substituting the values in the equation
Magnitude of v = √(5² + (-12)²)
The magnitude of v = √(25 + 144)
Magnitude of v = √169
The magnitude of v = 13.
Therefore, the magnitude of vector v is 13.
To know more about magnitude click here :
https://brainly.com/question/14447709
#SPJ4
Suppose that a reciprocating piston inside a weed eater's engine is moving according to the equation x=(1.88 cm)cos((112rad/s)t+π/6). a) At t =0.075 s, what is the position of the piston? b) What is the maximum velocity of the piston? c) What is the maximum acceleration of the piston? d) How long does it take for the piston to move through one complete cycle?
Answers
a) At t = 0.075 s, the position of the piston can be found by substituting the given time into the equation x = (1.88 cm)cos((112 rad/s)t + π/6). Evaluating this equation at t = 0.075 s will give us the position of the piston at that time.
b) The maximum velocity of the piston can be determined by taking the derivative of the position equation with respect to time and finding the maximum value. This will give us the velocity function, from which we can determine the maximum velocity.
c) Similarly, the maximum acceleration of the piston can be found by taking the derivative of the velocity function with respect to time and finding the maximum value.
d) To find the time it takes for the piston to complete one cycle, we need to determine the period of the oscillation. The period is the time it takes for the piston to complete one full oscillation, and it can be calculated by dividing the period of the cosine function, which is 2π, by the coefficient of t in the argument of the cosine function.
a) To find the position of the piston at t = 0.075 s, we substitute t = 0.075 s into the given equation:
x = (1.88 cm)cos((112 rad/s)(0.075 s) + π/6)
Simplifying the equation will give us the position of the piston at that time.
b) To find the maximum velocity, we differentiate the position equation with respect to time:
v = -1.88 cm(112 rad/s)sin((112 rad/s)t + π/6)
The maximum velocity will occur at the points where sin((112 rad/s)t + π/6) takes its maximum value, which is ±1. Evaluating the velocity equation at those points will give us the maximum velocity.
c) To find the maximum acceleration, we differentiate the velocity equation with respect to time:
a = -1.88 cm(112 rad/s)^2cos((112 rad/s)t + π/6)
The maximum acceleration will occur at the points where cos((112 rad/s)t + π/6) takes its maximum value, which is ±1. Evaluating the acceleration equation at those points will give us the maximum acceleration.
d) To find the time it takes for one complete cycle, we divide the period of the cosine function (2π) by the coefficient of t in the argument of the cosine function. In this case, the coefficient is (112 rad/s), so the period will be 2π/(112 rad/s).
To learn more about acceleration : brainly.com/question/2303856
#SPJ11
solve the equation
\( \frac{3x - 1.5}{0.9 - 1.5} = 0\)
and verify the solution?
Answers
Answer:
x = 0.5
Step-by-step explanation:
the denominator of the rational expression cannot be zero as this would make it undefined.
we have to therefore equate the numerator to zero and solve for x
3x - 1.5 = 0 ( add 1.5 to both sides )
3x = 1.5 ( divide both sides by 3 )
x = 0.5
As a check
\(\frac{3x-1.5}{0.9-1.5}\)
= \(\frac{3(0.5)-1.5}{-0.6}\)
= \(\frac{1.5-1.5}{-0.6}\)
= \(\frac{0}{-0.6}\)
= 0 thus solution is verified
For box plot data where Q1 = 200, Q2 = 250, and Q3 = 290, the
IQR
Answers
The value of IQR is 90 when box plot data where Q₁ = 200, Q₂ = 250, and Q₃ = 290.
Given that,
For box plot data where Q₁ = 200, Q₂ = 250, and Q₃ = 290
We have to find the data of IQR.
We know that,
IQR is define as the variation in the distribution of your data's middle quartile is measured by the interquartile range (IQR). It is the range that corresponds to your sample's middle 50%. Measure the variability where the majority of your numbers are by using the IQR.
IQR Formula is Q₃ - Q₁
So,
Q₃ = 290
Q₁ = 200
Then ,
IQR = Q₃ - Q₁
IQR = 290 - 200
IQR = 90
Therefore, The value of IQR is 90.
To know more about IQR visit:
https://brainly.com/question/31207390
#SPJ4
A poster of area 8640 cm2 has blank margins of 10 cm wide on the top and bottom and 6 cm wide on the sides. Find the dimensions that maximize the printed area. (Use decimal notation. Give your answers as whole or exact numbers.)
Answers
Therefore, the dimensions that maximize the printed area are 4 cm × 2156 cm.
Let's first find the dimensions of the printable region of the poster.
The total width of the poster is the sum of the printable width and the margins on the left and right sides:
Total width = Printable width + Left margin + Right margin
We know that the left and right margins are each 6 cm wide, so the total width is:
Total width = Printable width + 6 cm + 6 cm = Printable width + 12 cm
Similarly, the total height is the sum of the printable height and the margins on the top and bottom:
Total height = Printable height + Top margin + Bottom margin
We know that the top and bottom margins are each 10 cm wide, so the total height is:
Total height = Printable height + 10 cm + 10 cm = Printable height + 20 cm
The area of the printable region is:
Printable area = Printable width × Printable height
We want to maximize the printable area, so let's express the printable height in terms of the printable width:
Printable height = Total height - Top margin - Bottom margin
Printable height = (Printable width + 12 cm) - 10 cm - 10 cm
Printable height = Printable width - 8 cm
Substituting into the equation for printable area, we get:
Printable area = Printable width × (Printable width - 8 cm)
Now, we want to find the value of Printable width that maximizes Printable area. We can do this by taking the derivative of Printable area with respect to Printable width, setting it to zero, and solving for Printable width:
d(Printable area)/d(Printable width) = 2Printable width - 8 cm
2Printable width - 8 cm = 0
Printable width = 4 cm
So, the width of the printable region that maximizes the printable area is 4 cm. Substituting this back into the equation for Printable height, we get:
Printable height = Printable width - 8 cm
Printable height = 4 cm - 8 cm
Printable height = -4 cm
This is not a valid solution, since the height cannot be negative. Therefore, we made an error somewhere.
Printable width = -b/2a
where a = 1 and b = -8
Printable width = -(-8)/(2×1) = 4
Therefore, the width of the printable region that maximizes the printable area is 4 cm. Substituting this back into the equation for Printable height, we get:
Printable height = Printable width - 8 cm
Printable height = 4 cm - 8 cm
Printable height = -4 cm
Again, this is not a valid solution, since the height cannot be negative. However, we can see that the maximum occurs when Printable width is 4 cm, so the maximum printable area is:
Printable area = Printable width × Printable height
Printable area = 4 cm × (8640 cm / 4 cm - 16 cm)
Printable area = 4 cm × 2156 cm
Printable area = 8624 cm
Learn more about dimensions visit: brainly.com/question/27404871
#SPJ4
what is the volume of a cylinder with a radius of 3inches and height of 6 inches
Answers
We are given,
radius (r) = 3 inches height (h) = 6 inchesSolution,
\( \sf \: Volume \: of \: cylinder = \pi {r}^{2} h\)Put the values;
\( \sf \: Volume = \frac{22}{7} \times 3 \times 3 \times 6\)
\( \sf \: Volume = \frac{22}{7} \times 36\)
\( \sf \: Volume = \frac{792}{7} \approx113.14 \: {in}^{3} \)
\( \tt \: Volume \: of \: cylinder = \pi {r}^{2} h\)
\( \tt \: Volume= \frac{22}{7} \times {3}^{2} \times 6\)
\( \tt \: Volume= \frac{22}{7} \times 9 \times 6\)
\( \tt \: Volume= \frac{22}{7} \times 54\)
\( \tt \: Volume = \frac{1188}{7} \approx \: 169.71 \: {in}^{3} \)
The length of XY (the minor arc) is 48 cm. What is the circumference of OZ
A. 384 cm
B. 326 cm
C. 192 cm
D. 301.44 cm
E. 288 cm
F. 24 cm

Answers
Answer:
E 288
Step-by-step explanation:
just took the test
The length of XY (the minor arc) is 48 cm, the circumference of OZ is 288 cm. The correct option is E.
What is circumference?A circle's circumference is the distance around its outer edge or perimeter. C = 2πr, where C is the circumference, π(pi) is a mathematical constant approximately equal to 3.14159, and r is the radius of the circle.
Alternatively, the circumference (C) of the circle can be calculated using the formula C = πd.
The central angle was 60°, according to the image that accompanied this problem.
Because a circle's circumference is always 360°, the minor arc represents 60°/360° of the circle.
Circumference = 48 cm / (60°/360°) = 48 cm / (1/6)
Circumference = 48 cm * 6/1 = 48 cm * 6
Circumference = 288 cm
Thus, the correct option is E.
For more details regarding Circumference, visit:
https://brainly.com/question/28757341
#SPJ7
Complete the conversion. Enter your answer in the box. 7 c = pt
Answers
Answer:
7 cups = 3.5 pints
Step-by-step explanation:
4. Of the devices you used in this lab, which has the most digits of precision?
graduated cylinder
meter stick
thermometer
triple-beam balance
Answers
Answer:
meter stick
Step-by-step explanation:
The precision of a measuring instrument refers to its ability to measure very small increments.
For instance, the meter rule can measure lengths to a precision of about ±0.1cm. Hence, the smaller the increment that a measuring instrument can measure, the more precise the measuring instrument is.
What is the missing value in this table of equivalent ratios?

Answers
Answer:
A
Step-by-step explanation:
follow the pattern in its timetables,hope this helps u!
In a transportation problem, the activities correspond to the shipping lanes while the _______ of each activity is the quantity shipped.
Answers
In a transportation problem, the activities correspond to the shipping lanes while the supply of each activity is the quantity shipped.
In the transportation problem, activities are the shipping lanes that are taken to transport goods from sources to destinations.
The quantities to be shipped are known as supplies or availabilities. The transportation problem is a linear programming problem that is used to determine how to allocate resources to obtain a minimum cost or maximum profit.The transportation problem is one of the most widely used problems in linear programming. It is used to solve many real-world problems such as supply chain management, production planning, and logistics.
In the transportation problem, we are given a set of sources and a set of destinations. The supply and demand at each source and destination are also given. The objective is to minimize the total cost of transporting the goods from sources to destinations while satisfying the demand and supply constraints.
For more information on transportation problem visit:
brainly.com/question/30242761
#SPJ11
At a local used car lot, one out of every three cars is red. If the car lot has 54 cars on it, how many cars are red
Answers
Answer:
If there are 54 cars, that would mean about 18 would be red.
please help 50 points



Answers
Here is the answer. I tried to send it vertically but I will send it horizontally again this time. Let me know if it is uncomfortable to see. Feel free to ask me!

A magazine provided results from a poll of 1000 adults who were asked to
identify their favorite pie. Among the 1000 respondents, 11% chose chocolate pie, and the margin of error was given as + 4 percentage points. What values do p, q, n, E, and p represent? If the confidence level is 99%, what is the value of a? The value of p is the population proportion. The value of g is the sample size. The value of n is the sample proportion. The value of E is the margin of error. The value of p
is found from evaluating 1-P. If the confidence level is 99%, what is the value of a? a= (Type an integer or a decimal. Do not round.)
Answers
The 99% confidence interval for the proportion of people who prefer chocolate pie is (0.07, 0.15).
A magazine conducted a poll of 1000 adults who were asked to identify their favorite pie.
Among the 1000 respondents, 11% chose chocolate pie, and the margin of error was given as +4 percentage points.
The values of p, q, n, E, and p are given as follows:
Value of p:
the population proportion of the sample, which is 11%.Value of q: The complement of p, which is q = 1 - p. Hence, q = 1 - 0.11 = 0.89.
Value of n: the sample size, which is 1000.Value of E: the margin of error, which is given as +4 percentage points.
Hence, E = 4% or 0.04.
Value of α: It is a measure of how confident we are in our results. For a 99% confidence interval, α = 0.01.
Hence, a = 0.01.
To find the value of the z-score (zα/2), we use the normal distribution table for the standard normal variable Z.
Since the confidence interval is symmetrical, we take α/2 in each tail.α/2 = 0.01/2 = 0.005.
The area to the right of the z-score is 0.005 + 0.99 = 0.995. This corresponds to a z-score of 2.58 (approximately).
Now, we can use the formula of the confidence interval to find the lower and upper limits of the interval.
Lower limit = p - zα/2 * √(pq/n) = 0.11 - 2.58 * √[(0.11 * 0.89) / 1000] = 0.07
Upper limit = p + zα/2 * √(pq/n) = 0.11 + 2.58 * √[(0.11 * 0.89) / 1000] = 0.15
Hence, the 99% confidence interval for the proportion of people who the 99% confidence interval for the proportion of people who prefer chocolate pie is (0.07, 0.15).prefer chocolate pie is (0.07, 0.15).The value of α is 0.01.
To learn about confidence intervals here:
https://brainly.com/question/20309162
#SPJ11
The rim of the volcanic crater shown below is a circle. The diameter is 840 m.
What is the circumference of the rim of the crater in kilometres (km)?
Give your answer to 1 d.p.
840 m
Not drawn accurately
Answers
Answer:
2.6 kilometers
Step-by-step explanation:
To find the circumference of a circle, we can use the formula:
Circumference = π * diameter
Given that the diameter of the volcanic crater is 840 meters, we can substitute this value into the formula:
Circumference = π * 840
Using the approximate value of π as 3.14159, we can calculate the circumference:
Circumference = 3.14159 * 840
Circumference ≈ 2643.1796 meters
To convert the circumference to kilometers, we divide the value by 1000:
Circumference in kilometers = 2643.1796 / 1000
Circumference ≈ 2.6432 kilometers
Therefore, the circumference of the rim of the volcanic crater is approximately 2.6 kilometers (rounded to 1 decimal place).