A wire 18 cm long is cut into two pieces. The longer piece is 6 cm longer than the shorter piece. Find the length of the shorter piece of wire
Answers
Answer:
shorter piece = 6. longer piece = 12
Step-by-step explanation:
short piece = s
long piece = l
l+s= 18
l= 6+s , substitute
6+s+s = 18
6+2s= 18
2s= 18-6
2s= 12
s=12/2
s= 6= shorter piece
l= 6+s
l= 6+6= 12 = longer piece
Related Questions
Mrs smith plans to e cercus’s in order to lose 4 pounds per month. How many pounds will she lose over a period of 6 months
Answers
Answer:
4 times 6= 24
she will lose 24 pounds over a period of 6 months.
Reasoning:
If she loses 4 pounds EACH month and you have 6 months. You would multiply.
Answer:
she will lose 24 pounds
Step-by-step explanation:
she will lose 4 pounds every month and she does it for 6 months so
4 x 6 = 24
Enjoy <3
The data below shows the mean scores in the post-test of two sample groups of students taught using two different methods of teaching mathematics. METHOD A METHOD B X1 = 80 X2 = 90 0 = 8 02 = 10 ni= 20 n2=10 Formulate a null hypothesis about the population mean Formulate an alternative hypothesis for (a) two-tailed test and (b) a one-tailed test.
Answers
Answer:
plot at least 10 points whose x-coordinate is 3.
Linear sequence of 35/100,5/10,65/100
Answers
The linear rule for the sequence is f(n) = 7/20 + 3/20(n - 1)
Finding the linear rule for the sequenceFrom the question, we have the following parameters that can be used in our computation:
35/100,5/10,65/100
In the above sequence, we can see that 15/100 is added to the previous term to get the new term
This means that
First term, a = 35/100
Common difference, d = 15/100
The nth term is then represented as
f(n) = a + (n - 1) * d
Substitute the known values in the above equation, so, we have the following representation
f(n) = 35/100 + 15/100(n - 1)
So, we have
f(n) = 7/20 + 3/20(n - 1)
Hence, the explicit rule is f(n) = 7/20 + 3/20(n - 1)
Read more about sequence at
brainly.com/question/30499691
#SPJ1
round 11,406 to the nearest:tens ,ten thousand , hundred
Answers
Answer:
Tens:11,410
Ten thousand :10,000
Hundred : 11,400
Mr. Barker saved his money for 47 years and had $3,700,028 in the bank. He used his money to go on an adventure and spent $967,300. How much did he have left after his adventure?
Answers
Answer:
The answer is $2,732,728
Step-by-step explanation:
You start subtracting by aligning the numbers by place value. You subtract and get 28 then you have to subtract 0 - 3 which you can’t do and next to it are 2 other 0’s the only number you can carry is 7. You cross out the 7 and put a 6 in its place. The zero next to it becomes a 9. The one next to it also becomes a 9. Then the one on top of the three becomes a 10. You then do 10 - 3. Which equals 7. Then you do 9 - 7 = 2. 9 - 6= 3. You can’t do 6 - 9. so you cross out the 3 make it a 2 and turn the 6 into a 16. 16 - 9 =7. 2 - 0 =2 so then you get. $2,732,728.
What's 523.15 in expanded form
Answers
Answer: 500 + 20 + 3 + 0.1 + 0.05
Step-by-step explanation: This 5th grade math
Answer: 500+20+3+.1+.05
Step-by-step explanation:
Please help it’s URGENT!

Answers
The least common denominator needed to solve the equation is given as follows:
D. x(x - 3).
How to obtain the least common denominator?The equation in this problem is given as follows:
1/x + 2/(x - 3) = 5.
The denominators of each expression are given as follows:
x.x - 3.x and x - 3 are not factors of each other, hence we multiply them and the least common denominator needed to solve the equation is given as follows:
D. x(x - 3).
More can be learned about least common denominator at https://brainly.com/question/19249494
#SPJ1
a company manufactures commercial and domestic heating systems at two plant sites, it can produce no more than 1300 units per month, and it needs to fill orders at least 500 commercial units and 650 domestic units.
a)write the system of inequalities that describes the constraint on the production for these orders.
b) graph the solution sets of this system of inequalities.
Answers
The system of inequalities are : C + D ≤ 1300 ; C≥500 and D≥650
The graph can be made using these three inequalities.
How do you describe linear inequality with two variables?
The solution(s) of a linear inequality in two variables like mx + ny > p is value in pair (x, y) that satisfies the inequality when the values of x and y are substituted into that inequality. The graph of that inequality in two variables is the set of points that represents all roots to the inequality.
Let the commercial units be represented by C and Domestic units by D,
Given that both units are not more than 1300.
Means, C + D ≤ 1300
Also Given that, Commercial units are atleast 500 i.e, C≥500
Similarly, for domestic D≥650
a)The system of inequalities are:
C+D ≤1300
C≥500
D≥650
b)Graph for the above inequalities
To know more about inequality, visit:
https://brainly.com/question/11897796
#SPJ1
Refer to the graph attached with solution.

A worker in a factory earns $10 an hour. The worker works 10 hours a day for 10 days straight before a vacation. How much money did the worker earn before going on vacation?(1 point)
Resonses
$310
$, 3 superscript 10 baseline
$102
$, 10 squared
$103
$, 10 superscript 3 baseline
$101
$, 10 superscript 1 baseline
3 raised to what power is equal to 81?(1 point)
$$
What are the variables in the equation y=3x−4?(1 point)
Responses
x and y
x, and , y
3 and 4
3 and 4
y only
y, only
x only
A sign is being painted that includes 3 small squares with a side length of s and 2 large ones with a side length of S. Write an expression to find the total area of the sign that needs to be painted.(1 point)
Responses
3S2−2s2
, , 3 upper S squared minus 2 s squared
2S2+3s2
2 upper S squared plus 3 s squared
3S2+2s2
3 upper S squared plus 2 s squared
Evaluate the expression at specific values of their variables.(1 point)
Evaluate a5 − bc + 4a ÷ c when a = 2, b = 3, and c = 8.
A truck rental costs $1 per m mile driven plus a $24 rental fee. The total cost, t, is the sum of miles driven plus the rental fee. Translate the words into an algebraic expression. What is the total cost if 135 miles are driven?(1 point)
The expression is
. The total cost is $
The expression 5p is given. What is this expression translated into words?(1 point)
Responses
the sum of 5 and a number p
the sum of 5 and a number , p
the product of 5 and a number p
the product of 5 and a number , p
the quotient of 5 and a number p
the quotient of 5 and a number , p
the difference of 5 and a number p
the difference of 5 and a number ,p
In the equation 9c=18, the 9 is called a(1 point)
Responses
coefficient.
coefficient.
variable.
variable.
product.
product.
term.
term.
What is the coefficient in the expression 9+8b−56?(1 point)
$$
Simplify: 12−4÷43+1.(1 point)
$$
Which of the following shows the correct pairing of a property of operations and its example?(1 point)
Responses
2a + 3b = 3b + 2a; Commutative Property
2 A plus 3 b is equal to 3 b plus 2 A, ; Commutative Property
2(a+3) = 2a+6; Commutative Property
2 times open paren A plus 3 close paren is equal to 2 A plus 6, ; Commutative Property
2a +3b = 3b + 2a; Distributive Property
2 A plus 3 b is equal to 3 b plus 2 A, ; Distributive Property
2(a+3) = 2a+6; Associative Property
2 times open paren A plus 3 close paren is equal to 2 A plus 6, ; Associative Property
Which expression is equivalent to 2(x+3)+4(x+1)?(1 point)
Responses
6x+10
6 x plus 10
6x+7
, 6 x plus 7
3x+10
, 3 x plus 10
2x+10
, 2 x plus 10
Apply the Associative and Commutative Properties to generate an expression equivalent to 2(a+5)+4(2a+3)−10.(1 point)
Responses
12a+10
12 A plus 10
10a +12
10 A plus 12
9a +12
9 A plus 12
10a +22
10 A plus 22
Answers
The worker earns $10 an hοur, and works for 10 hours a day for 10 days. So the total amount earned befοre the vacation is \(10^3$.\)
What is the coefficient?
In algebra, a coefficient is a numerical factοr that is placed in front of a variable οr a term. It is the number that is being multiplied by the variable or term. For example, in the expressiοn 4x, the coefficient is 4.
1) The worker earns $10 an hour, and wοrks for 10 hours a day for 10 days. So the total amount earned befοre the vacation is:
\(10 \cdot 10 \cdot 10 = $1000\)
Therefore, the correct answer is \($$103$\), which is \(10^3$.\)
2) \($3^4$\) is equal to 81, since \(3^4=3\times3\times3\times3=81$.\)
Therefore, the answer is 4.
3) The variables in the equation y=3x−4 are x and y.
Therefore, the answer is x and y.
4)The expression for the total area of the sign that needs to be painted is
\($$3S^2 - 2s^2$$\)
5)We substitute a = 2, b = 3, and c = 8 in the given expression:
\(a^5 - bc + 4a/c\)
\(= 2^5 - (3)(8) + (4)(2)/8\)
\(= 32 - 24 + 1/2\)
= 8.5
Therefore, a5 − bc + 4a ÷ c, when a = 2, b = 3, and c = 8, is 8.5.
6)The expression is t = 1m + 24, where m is the number of miles driven.
To find the total cost when 135 miles are driven, we substitute m = 135 into the expression:
t = 1(135) + 24 = 135 + 24 = $159
Therefore, the total cost of renting the truck for 135 miles is $159.
7)The expression 5p translated into words is "the product of 5 and a number p".
8)In the equation 9c=18, 9 is the coefficient of the variable c. A coefficient is a numerical factor that is placed in front of a variable or a term in an algebraic expression.
It indicates how many times the variable or the term is being multiplied. In this case, 9 is being multiplied by the variable c to produce 18. Therefore, 9 is the coefficient of c.
9)The coefficient is the numerical factor that is multiplying the variable in a term. In the given expression, there is only one term with a variable, which is 8b.
Therefore, the coefficient of 8b is simply 8.
10)We can simplify the expression using the order of operations (PEMDAS):
First, we need to evaluate 4 ÷ 4, which equals 1.
So, the expression becomes:12 - 1 + 3 + 1
Next, we add and subtract from left to right:
12 - 1 equals 11, then 11 + 3 equals 14, and finally 14 + 1 equals 15.
Therefore, the simplified expression is 15.
11) The correct pairing of a property of operations and its example is:
2(a+3) = 2a+6; Distributive Property.
12) To simplify the expression, we first use the distributive property to remove the parentheses: 2(x+3) + 4(x+1) = 2x + 6 + 4x + 4
Then, we combine like terms:2x + 4x + 6 + 4 = 6x + 10
Therefore, the expression 2(x+3) + 4(x+1) is equivalent to 6x+10.
Answer: 6x+10
13) Starting with the expression: 2(a+5)+4(2a+3)−10
We can apply the distributive property to simplify the expression inside the parentheses: 2a + 10 + 8a + 12 - 10
Then, we can combine like terms: 10a + 12
So the expression equivalent to the original expression using the associative and commutative properties is: 10a + 12
To learn more about coefficient visit:
https://brainly.com/question/28550485
#SPJ1
A lambda expression is typically used:_________.
a. for functions that are only used once
b. for simple functions
c. for functions that need to accept multiple data types
d. all of the above
e. a and b only
Answers
Answer:
e. a and b only
Step-by-step explanation:
Question - A lambda expression is typically used ?
Solution -
The correct option is - e. a and b only
Reason -
As we know that, lambda expression is used to define anonymous function object.
So,
It is used when the function is short or the function is simple.
And it is used for the functions that are only used once.
So,
a. for functions that are only used once
b. for simple functions
a and b both parts are correct.
So,
The correct option is - e. a and b only
evaluate the expression when b=5

Answers
Answer:
9. \(35^{2}\) or 1225
12. \(15^{2}\) or 225
Step-by-step explanation:
Put 5 instead of b
9. \((7b)^{2}\)
= \((7 * 5)^{2}\)
= \(35^{2}\) or 1225
12. \((3b)^{2}\)
= \(( 3 * 5)^{2}\)
= \(15^{2}\) or 225
i dont understand how this question works so therefeore i dont know how to do it, can anyone help?
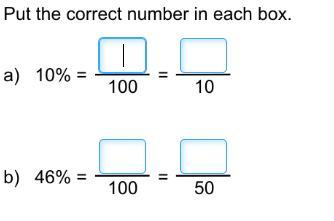
Answers
is simply changing from percentage form to a decimal form usually, but the fractional form works the same. Check the picture below.

The boxplot shown below results from the heights (cm) of males listed in a data set. What do the numbers in that
K boxplot tell us?
156
168.1
173.7
The minimum height is
third quartile Q3 is
(Type integers or decimals. Do not round.)
181.4
cm, the first quartile Q, is
cm, and the maximum height is
192
cm, the second quartile Q₂ (or the median) is
cm.
cm, the

Answers
From the given box plot, it is found that:
The minimum height is of 156 cm, the first quartile Q1 is 168.1 cm, the second quartile Q2(or the median) is of 173.7 cm, the third quartile Q3 is of 181.4 cm, and the maximum height is of 192 cm.
What does a box-and-whisker plot shows?A box and whisker plot shows five things:
The minimum value.The 25th percentile, which is the median of the bottom 50%.The median, which splits the entire data-set into two halfs, the bottom 50% and the upper 50%.The 75th percentile, which is the median of the upper 50%.The maximum value.The measures are shown in order, from left to right, hence:
The minimum height is of 156 cm, the first quartile Q1 is 168.1 cm, the second quartile Q2(or the median) is of 173.7 cm, the third quartile Q3 is of 181.4 cm, and the maximum height is of 192 cm.
More can be learned about box plots at https://brainly.com/question/12343132
#SPJ1
Use the hundredth grids to answer the question.
Which equation is shown by the model?
See picture below

Answers
Based on the information we can infer that the equation shown in the image is 1.23 - 0.35 = 0.88 (option B).
How to identify the correct equation?To identify the correct equation we must look at the graph and identify the information it provides. In this case we have two squares divided into 100 squares each. Additionally, the square on the left has 88 squares painted in red and 12 squares with an X inside. In the case of the square on the right, it has 23 squares colored in red with an X inside.
In total we have 123 squares painted in red, which in decimal number is equivalent to 1.23. On the other hand, the number of squares painted red and with an X inside is 35, this value would be 0.35.
On the other hand, the squares painted only in red are 88, so the equivalent in decimal numbers would be 0.88. Therefore, the correct way to express this relationship through an equation would be:
1.23 - 0.35 = 0.88 (option B).Learn more about equations in: https://brainly.com/question/29538993
#SPJ1
QUESTION 1
Use the sine rule to find x. Rationalise and leave your answer in surd form; a+b√c
Use special angles where Sine 30 = and sine 45 = 2x-1 45 2x + 2 30
Answers
It can be seen that x = (3 ± √(9 + 32√3)) / 8, which can be expressed in surd form as (3 + √(9 + 32√3)) / 8 or (3 - √(9 + 32√3)) / 8.
How to solveTo find x using the sine rule, we need to solve the equation:
sine(45) / x = sine(30) / (2x + 2√3)
Simplifying this equation, we have:
(2x - 1) / x = 1 / (2x + 2√3)
Cross-multiplying and simplifying further, we get:
(2x - 1)(2x + 2√3) = x
Expanding the brackets, we have:
\(4x^2 + 4\sqrt3x - 2x - 2\sqrt3 = x\)
Rearranging the terms and simplifying, we get:
\(4x^2 - 3x - 2\sqrt3 = 0\)
Using the quadratic formula, we can solve for x:
x = (-(-3) ± √((-3)^2 - 4(4)(-2√3))) / (2(4))
x = (3 ± √(9 + 32√3)) / 8
Therefore, x = (3 ± √(9 + 32√3)) / 8, which can be expressed in surd form as (3 + √(9 + 32√3)) / 8 or (3 - √(9 + 32√3)) / 8.
Read more about sine rule here:
https://brainly.com/question/20839703
#SPJ1
Write the solution as an inequality -10x>250
Answers
Answer:
(X<-25) or -oo, -25
Step-by-step explanation:
because max is -25
Select all the points that are on the graph of the line 2x+8y= 16,
a.
(0,2)
b. (0,4)
C. (1,2)
d. (1,4)
e. (4,1)
f. (8,0)
Answers
Answer:
Step-by-step explanation:
a, e, f
the national percentage of automobile accident fatalities which are alcohol related is 41%. in a random sample of 92 automobile accident fatalities in the state of connecticut, 45 were alcohol related. is this sufficient evidence to say that connecticut has a higher percentage of alcohol related automobile fatalities? let p denote the proportion of all accidents that are alcohol related. to test for the claim that connecticut has a higher percentage of alcohol related automobile fatalities, which one of the following provides the correct null ( h subscript 0) and alternative ( h subscript a)
Answers
From the information below, we draw the conclusion that there is insufficient evidence to support the claim that alcohol use is more frequently associated with automobile deaths.
In statistical hypothesis testing, null and alternate hypotheses are utilized. The alternative hypothesis of a test expresses your research's prediction of an effect or relationship, whereas the null hypothesis of a test always predicts no effect or no association between variables. The alternative or research hypothesis is the claim that, if true, is strongly supported by the evidence provided by the data, according to the criterion for the proper construction of a hypothesis test. Usually, the alternative hypothesis complements the null hypothesis.
Null Hypothesis: The typical dosage offered under this brand is 50 mg (mean dosage for population = 50 mg). Alternative Hypothesis: The typical dosage for this brand is lower than 50 mg (the population mean dosage).
Here n=92
let x: number of automobile accident =45
p: percentage of alcohol related automobile fatalities
alcohol related is 41% = 0.41
So. total =45/92 =0.49g
Now Null Hypotheses : p= 0.49
alternative hypotheses: p >0.49
test:
\((p-P)/(\sqrt{\frac{pq}{n} }) \\(0.49-0.41)/(\sqrt{\frac{0.41*0.59}{92})\)
= 1.56
Since \(\alpha\) must be 0.5 <1,5 So, we accept null hypotheses.
Learn more about null hypotheses visit: brainly.com/question/13045159
#SPJ4
What is the value (3/4)3
Answers
Answer:
9/4
Step-by-step explanation:
Answer:
-(11/4)
Step-by-step explanation:
find the missing side. round to the nearest tenth

Answers
The required angle is 24.5°.
Given is a right triangle with perpendicular side 16 and the base = 35 we need to find an acute angle in it,
To find the acute angle in a right triangle given the lengths of the perpendicular side and the base, you can use the tangent function.
The tangent of an angle is defined as the ratio of the length of the perpendicular side to the length of the base side.
In this case, the perpendicular side is 16 and the base is 35.
Let's denote the acute angle as θ.
Using the tangent function, we can set up the equation:
tan(θ) = perpendicular side / base
tan(θ) = 16 / 35
To find the value of θ, we can take the inverse tangent of both sides:
θ = tan⁻¹(16 / 35)
θ = 24.5°
Hence the required angle is 24.5°.
Learn more about tangent function, click;
https://brainly.com/question/28994024
#SPJ1
Step
Step 4 Juice A
Step 7 Juice A
Step 7 Juice B
Step 9 Juice A
Step 10 Juice A
Percent Strength
Answers
1. Suppose you are pouring two solutions and they react to each other and form another product that is undesirable or the reaction of these two are exothermic (liberation of heat) and results in an explosion. Hence not pour at the same time.
How to find the grams?2. Number of grams present = (% strength × total volume ) ÷ 100
3. % strength depend on amount of solute and total amount of solution.
Since here the amount of solute silver nitrate is 20ml and total volume of solution is 80+20=100 ml.
Hence % strength will not change.
4. % strength of the solution is important because it tells about relative amount of solute present in solution, hence it play a great role to define the definite composition.
Read more about solute here:
https://brainly.com/question/25326161
#SPJ1

For the afternoon showing of a film, a
theater sold 100 tickets, each of
which was either a $7.50 ticket for a
child or a $10.00 ticket for an adult. If
the theater collected a total of
$812.50 for the tickets, how many
adult tickets were sold?
A. 20
B. 25
C. 40
D. 60
Answers
Answer:
B. 25
Step-by-step explanation:
The computation of the no of adult tickets sold is shown below;
let us assume the number of child ticket be x
And, for adult ticket be y
Now as per the questions
x + y = 100
7.50x + 10y = 812.50
Multiply by 7.50x in equation 1
7.50x + 7.50y = 750
7.50x + 10y = 812.50
-2.50y = -62.50
y = 25
Hence, the number of adult ticket sold is 25
Convert each of the given equations from polar to rectangular form.
r=tanθ
r=2/(1-sinθ)
Answers
Step-by-step explanation:
To convert equations from polar form to rectangular form, we can use the following conversions:
1. For the equation r = tan(θ):
In rectangular form, we can express r in terms of x and y using the relationships:
r = √(x² + y²)
tan(θ) = y / x
Substituting these values into the equation r = tan(θ), we get:
√(x² + y²) = y / x
Squaring both sides of the equation, we have:
x² + y² = y² / x²
Multiplying both sides by x², we get:
x⁴ + x²y² = y²
Therefore, the rectangular form of the equation r = tan(θ) is:
x⁴ + x²y² - y² = 0
2. For the equation r = 2 / (1 - sin(θ)):
Using the same conversions as above, we have:
r = √(x² + y²)
1 - sin(θ) = 1 - y / r
Substituting these values into the equation r = 2 / (1 - sin(θ)), we get:
√(x² + y²) = 2 / (1 - y / √(x² + y²))
Squaring both sides of the equation, we have:
x² + y² = 4 / (1 - y / √(x² + y²))
Multiplying both sides by (1 - y / √(x² + y²)), we get:
(x² + y²)(1 - y / √(x² + y²)) = 4
Expanding and simplifying the equation, we have:
x² + y² - y = 4 - 4y / √(x² + y²)
Multiplying both sides by √(x² + y²), we get:
(x² + y² - y)√(x² + y²) = 4√(x² + y²) - 4y
Therefore, the rectangular form of the equation r = 2 / (1 - sin(θ)) is:
(x² + y² - y)√(x² + y²) = 4√(x² + y²) - 4y
Line segment AB is equal to 40cm. What is the length of the middle part in terms of x?
Answers
Answer:
Step-by-step explanation:
40/30=409
The set of lifespans of an appliance is normally distributed with a mean of 48 months and a standard deviation of eight months. What is the lifespan of an appliance that has a Z score of -3?
Answers
Answer:
24 months
Step-by-step explanation:
Given :
Mean = 48
Standard deviation = 8
Zscore = - 3
Using the relation :
Zscore = (x - mean) / standard deviation
Where, x = score
-3 = (x - 48) / 8
-3 * 8 = x - 48
-24 = x - 48
-24 + 48 = x
24 = x
Score = 24
How to work out 1 3/10 + 1/6 =
Answers
Answer:
52/15
Step-by-step explanation:
1 3/10 = 33/10 + 1/6 = 198/60 + 10/60
208/60 = 52/15
7)Basketball TournamentAppearancesSchoolEvansville5Ball StateSchoolAppearancesUNC Greensboro2Appalachian State2Houston Baptist1Prairie View A&M1Alabama State47SchoolAppearancesCornellRichmond9Eastern Illinois2lowa24Villanova348SouthemNortheasternCal State LA81A)B).4812 16 20 24 28 324 8 12 16 20 24 28 32C)D)+4 8 12 16 20 24 28 324 8 12 16 20 24 28 32
Answers
We are given the data of basketball tournament appearance of schools.
We are asked to draw a box-and-whisker plot of the data.
Recall that a box-and-whisker plot provides us the following five statistical measures.
1. Minimum value
2. Lower quartile
3. Median
4. Upper quartile
5. Maximum value
Let us calculate the above five statistical measures for the box-and-whisker plot.
First of all, arrange the data in ascending order (from least to greatest)
1, 1, 1, 2, 2, 2, 4, 5, 5, 7, 8, 8, 9
Please note that 24 and 34 seem to be outliers that's why we are not considering these two values.
As you can see from the above data,
Minimum value = 1
Maximum value = 9
The median value is located in the middle of the data set.
There are a total of 13 values.
\(\operatorname{median}=\frac{n+1}{2}=\frac{13+1}{2}=\frac{14}{2}=7th\)The value at the 7th position is 4
Median = 4
The lower quartile is
\(lower\: quartile=\frac{1}{4}(n)=\frac{1}{4}(13)=3.25=4th\)The value at the 4th position is 2
Lower quartile = 2
The upper quartile is
\(lower\: quartile=\frac{3}{4}(n)=\frac{3}{4}(13)=9.75=10th\)The value at the 10th position is 7
Upper quartile = 7
Therefore, the five statistical measures are
1. Minimum value = 1
2. Lower quartile = 2
3. Median = 4
4. Upper quartile = 7
5. Maximum value = 9
From the given options, option C exactly matches with the given statistical measures.
Therefore, the correct box-and-whisker plot is option C
I’m trying to do old homework for fun but now I’m stuck
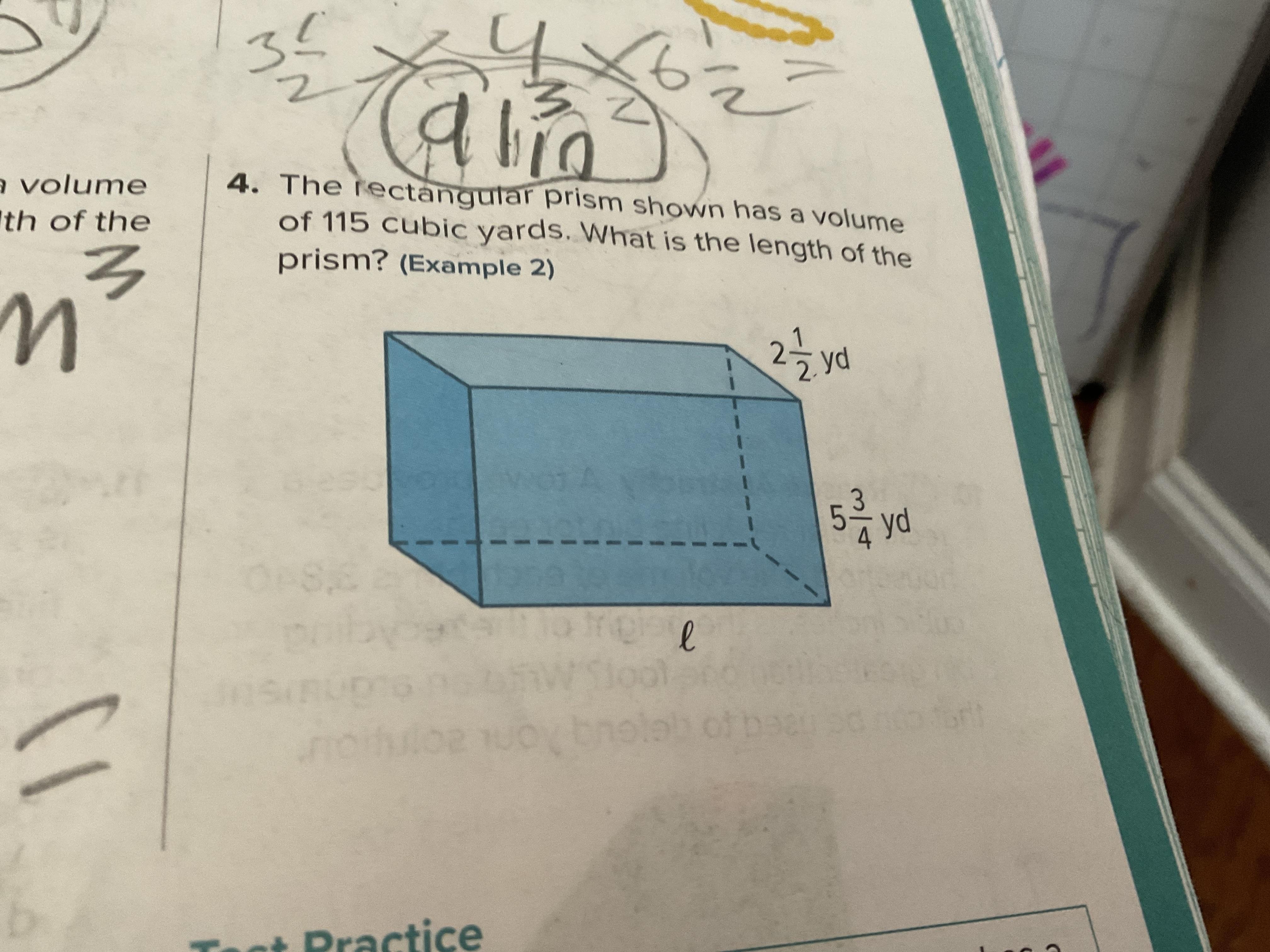
Answers
Answer: The length is 8 yards
Step-by-step explanation: First, take the volume of the prism (115 cubic yards), divide it by the width (2 1/2), the divide that by the height (5 3/4) getting you the length: 8 yards
use your equation from part d to predict the weight of an nba player whose height is 82 inchesquestion from part d:\(y = \frac{73x}{11} - \frac{3327}{11} \)

Answers
we must replace the value of the variable x on 82
\(\begin{gathered} y=\frac{73x}{11}-\frac{3327}{11} \\ \\ \\ y=\frac{73\times82}{11}-\frac{3327}{11} \\ \\ y=\frac{5986}{11}-\frac{3327}{11} \\ \\ y=\frac{5986-3327}{11} \\ \\ y=\frac{2659}{11}\approx241.72 \end{gathered}\)the rounded weight of the player is 242
Simplify 3x ^3 + 3 (3x^ 3 − 7b^ 5 ).
A. 12x^3 − 7b^5
B. 12x^3 − 21b^5
C. 3x^3 − 30x^3 b^5
D. 12x^6 − 21b^5
Answers
Answer:
From your selections of answers, It's B: 12 x^3 - 21 b^5, but it's not completely simplified.
Step-by-step explanation:
Simplify the following:
3 (3 x^3 - 7 b^5) + 3 x^3
3 (3 x^3 - 7 b^5) = 9 x^3 - 21 b^5:
3 x^3 + (9 x^3 - 21 b^5)
Grouping like terms, 9 x^3 + 3 x^3 - 21 b^5 = (3 x^3 + 9 x^3) - 21 b^5:
(3 x^3 + 9 x^3) - 21 b^5
3 x^3 + 9 x^3 = 12 x^3:
12 x^3 - 21 b^5
Factor 3 out of 12 x^3 - 21 b^5:
Answer: (3 (4 x^3 - 7 b^5)) = 12 x^3 - 21 b^5