Abby is registering at a Web site and must select a six-character password.The password can contain either letters or digits.
a.How many passwords are possible if characters can be repeated? if no characters can be repeated?
b.How many passwords are possible if all characters are letters that can be repeated? if the password must contain exactly one digit? Which type of password is more secure? explain
Answers
Answer:
a. 2176782336 with repeated characters. 1402410240 with no repeated characters.
b. 7964171460 when all letters can be repeated, but not numbers. 118813760 when only one number and letters can be repeated.
I believe that the password with all letters able to repeat and numbers not being able to is the most secure password, because if someone were to guess the password there is a 1/7964171460 chance of guessing the password.
Step-by-step explanation:
A. Since there are 26 different letters and 10 different numbers, there are 36 characters we can type. If characters can be repeated then, there is 2176782336 different passwords, since on all six number there are 36 possibilities each. So, 36 x 36 x 36 x 36 x 36 x 36 or 36^6 is to evaluated to find the answer. If characters are not to be repeated, there are 1402410240 different passwords, since on the first number there are 36, second has 35, third has 34, fourth has 33, fifth has 32, and sixth has 31. So, 36 x 35 x 34 x 33 x 32 x 31 is to be evaluated to solve this.
B. Since all characters that are letters can be repeated, then there are 26 letters to use forever and 10 numbers you can use with a limit. So, 36 x 35 x 34 x 33 x 32 x 31 which is to be solved if only numbers were to be used, which is 1402410240. Then, you add that with 36 x 35^5 and 36 x 35 x 34^4 and 36 x 35 x 34 x 33^3 and 36 x 35 x 34 x 33 x 32^2. which will be 7964171460. If the password must contain one digit, then you must multiply 10 with 26^5. Since, there is 10 different digits to use for the first number and 26 letters to choose from for the other five. So, it will be 26^5 times 10 which is 118813760.
Related Questions
About how many centimeters are in 6.25 inches if 1 inch is about 2.5 centimeters? Show your reasoning.
heheheheheh im so smarts (not really)
Answers
Answer:
6.25inch=15.625cm
Step-by-step explanation:
1inch=2.5cm
6.25*2.5=15.625cm
Given RS = 6, ST = 3, and SL = 4, find the required measure. (Part of the answer is provided for you.)
KT =
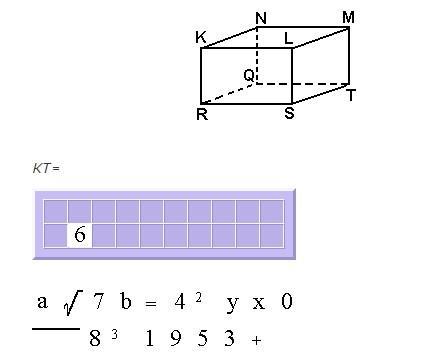
Answers
Answer:
https://brainly.com/question/1593288
Step-by-step explanation:
This was answered previously on here
Answer:
Square root of 61
Step-by-step explanation:
It was correct on my assignment
BRAINLIST!!!!!!!!!
which one is a function???

Answers
Answer: C
i hope this helps
please help me with math pt.1

Answers
Answer:
i don't think you're in high school
#1. 15.84 (6.6 * 2.4)
#2 193.2 (27.6 * 7)
#3 B and E
Step-by-step explanation:
6.6 * 2.4
27.6 * 7
Answer:
No. of miles Jake rode today = 6.6×2.4 times
= 15.84 miles
1 gallon of gas = 27.6 miles
7 gallons of gas = 193.2 miles
Myla's car can go 193.2 miles with 7 gallons of gas.
All expressions except 7.33×6.
a rectangle field is four times as long as it's wide if the length is decreased by 10 ft and the width is increased by 2 ft the perimeter will be 80 ft find the dimensions of the original field the original dimensions are blank feet long by blank feet wide
Answers
Let the width of the field = w
∵ The length is four times as the width
∵ The width = w
∴ The length = 4w
∵ The length is decreased by 10 feet
∴ The new length = 4w - 10
∵ The width is increased by 2 feet
∴ The new width = w + 2
The new perimeter is 80 feet
∵ The perimeter of the rectangle = 2(length + width)
\(\therefore P=2(4w-10+w+2)\)Let us simplify it
\(\begin{gathered} P=2(4w+w-10+2) \\ P=2(5w-8) \\ P=2(5w)-2(8) \\ P=10w-16 \end{gathered}\)Now equate it by 80
\(10w-16=80\)Add 16 to both sides
\(\begin{gathered} 10w-16+16=80+16 \\ 10w=96 \end{gathered}\)Divide both sides by 10
\(\begin{gathered} \frac{10w}{10}=\frac{96}{10} \\ w=9.6 \end{gathered}\)The length is 4 times the width
\(\begin{gathered} l=4(9.6) \\ l=38.4 \end{gathered}\)The length is 38.4 feet and the width is 9.6 feet
**URGENT PLEASE HELP SOON** Each brick in the wall has the dimensions shown below. A rectangular prism with a length of 8 inches, width of 4 inches, and height of 2.25 inches. What is the volume of each brick?
Options:
56 in^3
72 in^3
118 in^3
144 in^3
Answers
The volume of each individual brick is 72 cubic inches.
How to get the volume of each brick?
The volume of a rectangular prism of height H, width W, and length L is given by:
V = L*H*W
In this case we have:
L = 8inW = 4inH = 2.25 inThen, replacing these in the volume equation, we get:
V = (8 in)*(4 in)*(2.25 in) = 72in³
So the correct option is the second one.
If you want to learn more about volume:
https://brainly.com/question/1972490
#SPJ1
Answer:
The volume of each individual brick is 72 cubic inches.
Step-by-step explanation:
How to get the volume of each brick?
The volume of a rectangular prism of height H, width W, and length L is given by:
V = L*H*W
In this case we have:
L = 8in
W = 4in
H = 2.25 in
Then, replacing these in the volume equation, we get:
V = (8 in)*(4 in)*(2.25 in) = 72in³
So the correct option is the second one.
Your friend is trying to see if you can guess the two numbers she secretly has written on her paper. Your friend tells you that 2 times the first number is 13 more than the second number. She also tells you that the sum of the two numbers is 62.
Can you guess your friend's numbers?
Answers
If your friend tells you that 2 times the first number is 13 more than the second number, the two numbers are 25 and 37.
Let's assume the first number is represented by x and the second number is represented by y. According to the given information, we can create two equations:
2x = y + 13 (Equation 1)
x + y = 62 (Equation 2)
We can use Equation 2 to solve for x:
x = 62 - y
We can substitute this value of x in Equation 1 to solve for y:
2(62 - y) = y + 13
124 - 2y = y + 13
124 = 3y + 13
111 = 3y
y = 37
Now that we have found y, we can substitute this value in Equation 2 to solve for x:
x + 37 = 62
x = 25
To learn more about number click on,
https://brainly.com/question/12660637
#SPJ1
If your company is worth $100,000 and you sell 10 shares of your company...
How much is each share worth?
This is a test!
Answers
Answer:
10
Step-by-step explanation:
dived them
the administration team compiled test results for those who had been tested for strep throat in a random sample of 400 sick patients who had been tested. the following relative frequency table shows the data. positive negative total has the flu 54% 6% 60% does not have the flu 8% 32% 40% total 62% 38% 100% based on the data, what is the ratio of false positives to true positives? 6 over 32 8 over 6 8 over 54
Answers
The ratio of false positives to true positives is 8 over 54.
According to the Question
Results of a strep throat test performed on a sample of 400 ill people are displayed in the table's data. People who have the flu and those who don't are separated into two categories. The patients are then separated into groups based on whether they tested positive or negative for strep throat within each of these categories.
We must first define what a true positive and a false positive are in order to calculate the ratio of false positives to true positives. A patient who tests positive for strep throat but does not actually have the illness is said to have a false positive. The 8% of patients in this instance who tested positive for strep throat but did not have the flu would fall under that category. A patient who tests positive for strep throat and truly has the illness is said to have a true positive. That would be the 54% of patients who tested positive for both the flu and strep throat in this instance.
We divide the percentage of false positives (8%) by the percentage of true positives (54%), which gives us the ratio of false positives to true positives.
As a result, the ratio becomes 8% / 54%, or 8/54.
It's critical to remember that this ratio is dependent on the sample and test performed and may not be the same for different populations or testing methodologies.
To know more about proportion and ratio on brainly :
brainly.com/question/26974513
#SPJ4
10 < w/6 solve the inequality for w and simplify your answer as much as possible
Answers
Answer:
60
Step-by-step explanation:
10 x 6 < w
60 < w
that answers it
Answer: Multiply to remove the fraction, then set equal to
0
and solve.
Inequality Form:
w
>
60
Interval Notation:
(
60
,
∞
)
a vineyard has 145 acres of chardonnay grapes. a particular soil supplement requires 5.50 g for every square meter of vineyard. how many kilograms of the soil supplement are required for the entire vineyard? (recall that 1 km2
Answers
3230 Kilograms of the soil supplement are required for the entire Vineyard.
Some units that need to be recalled are as follows:
1 km = 1000 m
1 km^2 = 1000000 m^2
1 km^2 = 247 acres
1 kg = 1000 g
Let's tackle the problem now:
A vineyard has 145 acres of Chardonnay grapes.
145 acres = \(\frac{145}{247}\)× 1 km^2
145 acres = 145/247 km^2
145 acres ~ 0.587 km^2
A particular soil supplement requires 5.50 grams for every square meter of vineyard
1m^2 → 5.50 gram
1 km^2 = 10^6 →5.50 x 10^6 gram
1 km^2 →5.50 x 10^6 x 10^-3 kg
1 km^2 →5.50 x 10^3 kg
145 acres = 145/247 km^2 →145/247 x 5.50 x 10^3 kg
145 acres → 797500/247 kg
145 acres → 3230 kg
It required 797500/247 kg ~ 3230 kg of the soil supplement for the entire Vineyard.
Learn more about Soil Supplement at:
https://brainly.com/question/1578028
#SPJ4
A coffee distributor needs to mix a(n) House coffee blend that normally sells for $9.50 per pound with a Terraza coffee blend that normally sells for $14.70 per pound to create 20 pounds of a coffee that can sell for $10.54 per pound. How many pounds of each kind of coffee should they mix
Answers
The coffee distributor should mix 16 pounds of House coffee blend with 4 pounds of Terraza coffee blend to create a 20-pound mixture that can sell for $10.54 per pound.
Let's assume x represents the number of pounds of House coffee blend to be mixed and y represents the number of pounds of Terraza coffee blend to be mixed.
We are given the following information:
House coffee blend cost per pound: $9.50
Terraza coffee blend cost per pound: $14.70
Desired selling price per pound of the mixture: $10.54
Total weight of the mixture: 20 pounds
To solve this problem, we can set up a system of equations based on the cost and weight of the coffee blends:
Equation 1: x + y = 20 (Total weight of the mixture is 20 pounds)
Equation 2: (9.50x + 14.70y) / 20 = 10.54 (Average cost of the mixture is $10.54 per pound)
Let's solve this system of equations:
From Equation 1, we can express x in terms of y:
x = 20 - y
Substituting x in Equation 2:
(9.50(20 - y) + 14.70y) / 20 = 10.54
Simplifying and solving for y:
(190 - 9.5y + 14.70y) / 20 = 10.54
(190 + 5.2y) / 20 = 10.54
190 + 5.2y = 210.8
5.2y = 210.8 - 190
5.2y = 20.8
y = 20.8 / 5.2
y = 4
Substituting y = 4 back into Equation 1:
x + 4 = 20
x = 20 - 4
x = 16
Therefore, the coffee distributor should mix 16 pounds of House coffee blend with 4 pounds of Terraza coffee blend to create a 20-pound mixture that can sell for $10.54 per pound.
For more details about mixtures
https://brainly.com/question/29080733
#SPJ4
How long will it take a $1000 investment to grow to $2000 if it earns 5. 5% compounded quarterly
Answers
It will take approximately 6.62 quarters, or 1.655 years, for a $1000 investment to grow to $2000 at an annual interest rate of 5.5% compounded quarterly.
To calculate this, we can use the formula for compound interest:
A = P * (1 + r/n)^(n*t)
Where:
A = the future value of the investment
P = the principal amount (initial investment)
r = the annual interest rate (5.5% in this case)
n = the number of times the interest is compounded per year (4 times quarterly in this case)
t = the time period (in years)
Plugging in the given values, we get:
A = 1000 * (1 + 0.055/4)^(4*t)
We want to find the time it takes for the investment to grow to $2000, so we can set A equal to $2000 and solve for t:
2000 = 1000 * (1 + 0.055/4)^(4*t)
2 = (1 + 0.055/4)^(4*t)
Taking the natural logarithm (ln) of both sides:
ln(2) = ln[(1 + 0.055/4)^(4*t)]
Using the property of logarithms that ln(a^b) = b*ln(a):
ln(2) = 4*t * ln(1 + 0.055/4)
Dividing both sides by 4*ln(1 + 0.055/4):
t = ln(2) / (4 * ln(1 + 0.055/4))
Simplifying this expression gives:
t ≈ 6.62 quarters
Therefore, it will take approximately 6.62 quarters, or 1.655 years, for a $1000 investment to grow to $2000 at an annual interest rate of 5.5% compounded quarterly.
Learn more about interest rate from
https://brainly.com/question/25720319
#SPJ11
Please help meeeeeee

Answers
Answer:
She earns $2,560
Step-by-step explanation:
She earns 2,560 because this is 8% of 32000. How do we know?
Multiply 32000 by 0.088, which is 8% of 100.
Stat 0,-10 and -6,-8
Answers
The midpoint of the given coordinates of points (0,-10) and (-6,-8) is ( -3,-9 )
How determine the midpoint between two point?A midpoint is simply a point that divides a line segment into two equal halves.
The midpoint formula is expressed as;
M = ( (x₁+x₂)/2, (y₁+y₂)/2 )
Given the data in the question;
Point 1( 0,-10 )
x₁ = 0y₁ = -10Point 2( -6,-8 )
x₂ = -6y₂ = -8Midpoint = ?
To determine the midpoint, plug the given points into the midpoint formula above and simplify.
M = ( (x₁+x₂)/2, (y₁+y₂)/2 )
M = ( ( 0 + (-6) )/2, ( (-10) + (-8) )/2 )
M = ( ( 0 - 6) )/2, ( -10 - 8 )/2 )
M = ( ( -6 )/2, (-18 )/2 )
Midpoint M = ( -3,-9 )
Therefore, the midpoint of the coordinates is ( -3,-9 ).
Learn more about the midpoint formula here: brainly.com/question/14687140
#SPJ1
The area of a parallelogram can be found by the equation area = (b)(h)
Find the height of a parallelogram that has an area of 10
1
2
in² and a base of
3
4
in.
The height of the parallelogram is
inches.
Answers
Answer:
14
Step-by-step explanation:
Answer:
answer: 14
Step-by-step explanation:
got it right
How far is the 100cm chord to the center of a circle with a radius of 26cm?
Need help here, Which formula should I use in any questions like this?
Answers
The distance between the chord to the center of the circle is 42.70 units.
What is a chord?The line segment joining the two points in the circle, the diameter, is the longest chord of the circle.
Given that, a circle has 100 cm of chord and 26 cm of radius, we need to find the distance between them,
Let the chord be AB and the radius be CA and the distance between them be AD,
Please refer to the figure,
We see that, the arrangement of the radius and chord are making a right triangle,
Therefore, using Pythagoras theorem,
AC² = AD² + CD²
50² = 26²+CD²
CD = 2500-676
CD = 42.70
Hence, the distance between the chord to the center of the circle is 42.70 units.
Learn more about Chord click;
https://brainly.com/question/2562191
#SPJ9

what is the probability that a student has a gpa under 2.0 given that he or she has skipped many classes?
Answers
The probability that a student has a GPA under 2.0 given that he has skipped many classes is 8/11.
From the table we see that,
The student who have a GPA under 2.0 = 80
The student who has skipped many classes = 80 + 25 + 5
The student who has skipped many classes = 110
Hence, the probability that a student has a GPA under 2.0 given that he has skipped many classes = The student who have a GPA under 2.0/The student who has skipped many classes
The probability that a student has a GPA under 2.0 given that he has skipped many classes = 80/110
The probability that a student has a GPA under 2.0 given that he has skipped many classes = 8/11
To learn more about probability link is here
brainly.com/question/14200898
#SPJ4
The complete question is:
One thousand students at a city high school were classified both according to GPA and whether or not they consistently skipped classes.
What is the probability that a student has a GPA under 2.0 given that he has skipped many classes?
A. 0.080
B. 0.281
C. 0.285
D. 0.314
E. 0.727

A salesperson at a jewelry store earns 6% commission each week. Last week, jarrod sold $680 worth of jewelry. How much did make in commission? How much did the jewelry store make from sales?
Answers
Answer:
1/ $ 4.08
2/ $675.92
Step-by-step explanation:
Take 68 times 0.06% = $4.08
680 - 4.08= 675.92
Answer:
Step-by-step explanation:
40.80 it told me the answer
Find the perimeter and area
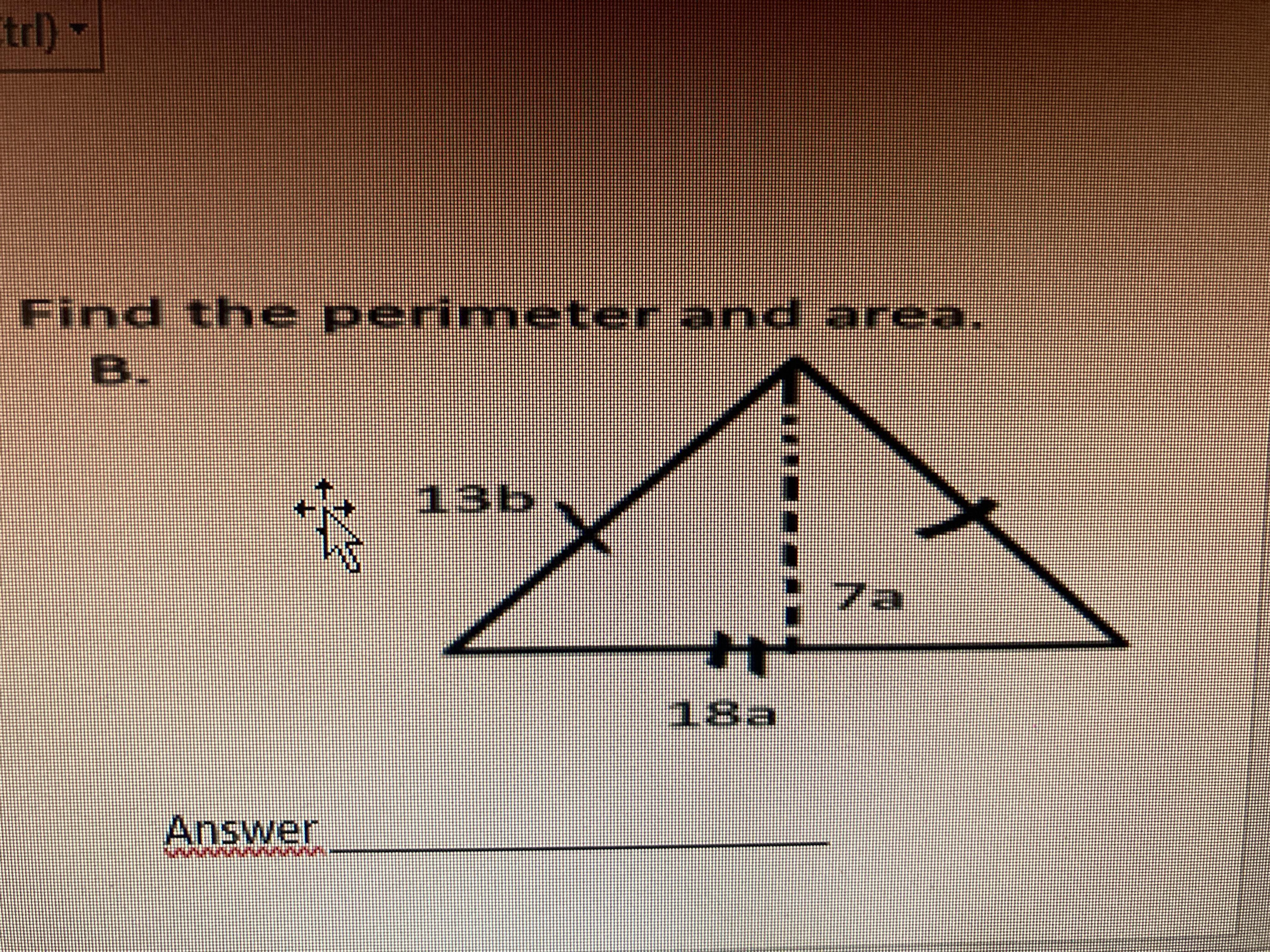
Answers
Answer:
The area is 63a
The perimeter is 39b
Step-by-step explanation:
Given two sequences
A) 3, 5, 7, 9, 11....
B) 3, 6, 12, 24...
Write the nth term of the above each sequence
Answers
Answer:
[See Below]
Step-by-step explanation:
✦ Given that \(y=x+2\) the next numbers would be:
✧ \(13\)
✧ \(15\)
✧ \(17\)
✧ \(19\)
✦ Given that \(y=x+x\) the next numbers would be:
✧ \(48\)
✧ \(96\)
✧ \(192\)
✧ \(384\)
✧ \(768\)
~Hope this helps Mate. If you need anything fell free to message me.
Type your solutions into this document and be sure to show all steps for arriving at your solution. Just giving a final number may not receive full credit. PROBLEM 1 A 125-page document is being printed by five printers. Each page will be printed exactly once. (a) Suppose that there are no restrictions on how many pages a printer can print. How many ways are there for the 125 pages to be assigned to the five printers? One possible combination: printer A prints out pages 2-50, printer B prints out pages 1 and 51-60, printer
Answers
The number of ways there for the 125 pages to be assigned to the four printers = 5^125 ways.
As per the question,
A 125-page document is being printed by four printers.
Each page will be printed exactly once.
There are no restrictions on how many pages a printer can print.
One of the possible combinations is that printer A prints out pages 2-50, printer B prints out pages 1 and 51-60, printer C prints out 61-80 and 86-90 and printer D prints out pages 81-85 and 91-100.
Since, there are no restrictions in printing the pages any printer cannot print even a single page and any printer can print all 125 pages. To print 100 pages we have four printers.
⇒ Number of possible ways a single paper can be assigned to the four printers = 4 ways
⇒ Number of possible ways 125 pages can be assigned to the four printers
= 5 × 5 × 5 × 5 .................... 5 ( a total of 125 terms )
= ways.
Therefore, In ways we can assign 125 pages to four printers with no restrictions.
To know more about assigning pages problem refer to:
brainly.com/question/25583761
#SPJ4
In a sale, the price of a book is reduced by 25%.
The price of the book in the sale is £12
Work out the original price of the book
Answers
Question: In a sale, the price of a book is reduced by 25%. The price of the book in the sale is £12. Work out the original price of the book
Answer: £16
Step-by-step explanation:
To determine the original price of the book, we can use the fact that the sale price is 75% (100% - 25%) of the original price. Let's denote the original price as x.
75% of x = £12
To solve for x, we can set up the equation:
0.75x = £12
To isolate x, we divide both sides of the equation by 0.75:
x = £12 / 0.75
x = £16
Therefore, the original price of the book was £16.
The mapping diagram represents a relation where x represents the independent variable and y represents the dependent variable. A mapping diagram with one circle labeled x-values containing values negative 8, negative 5, negative 1, 1, and 12 and another circle labeled y values containing values negative 4 and negative 2 and arrows from negative 8 to negative 4, negative 5 to negative 2, negative 1 to negative 2, 1 to negative 2, 12 to negative 4, and 12 to negative 2. Is the relation a function? Explain. Yes, because for each input there is exactly one output Yes, because for each output there is exactly one input No, because for each input there is not exactly one output No, because for each output there is not exactly one input
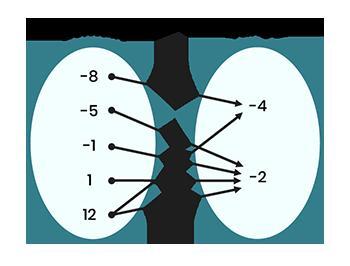
Answers
Is the relation a function: C. No, because for each input there is not exactly one output.
How to determine the relationships that represent functions?In Mathematics, a function is typically used for uniquely mapping an independent value (input variable or domain) to a dependent value (range or output variable).
This ultimately implies that, an independent value represents the value on the x-axis of a cartesian coordinate while a dependent value represents the value on the y-axis of a cartesian coordinate.
Since the independent value (12) is mapped to multiple dependent values (-4 and -2), we can logically deduce that the relation does not represent a function.
Read more on function here: brainly.com/question/3632175
#SPJ1
Find square root of 3-4i
Answers
The correct answer is ±(2-i).
Given function,
√3-4i
Further solving,
Assume,
√3-4i = x + iy
3 - 4i = x² - y² + 2ixy
Comparing both sides,
x² - y² = 3......(1)
2ixy = -4i
So,
xy = -2........(2)
(x² + y²)² = (x² - y²)² + 4x²y²
= 3² + (-4)²
= 25
(x² + y²)² = 25
(x² + y²) = 5.........(3)
from 1 and 3
x² = 4
x = ±2
y² = 1
y = ±1
Thus the square root of 3 - 4i is ±(2-i).
Know more about complex functions,
https://brainly.com/question/30241589
#SPJ1
Why is i squared equal to 1?
Answers
The square root of -1 is the definition of i. A square root is squared to eliminate the two and leave the original number.
Given that,
We have to find why i squared is equal to negative 1.
We know that,
The imaginary numbers are denoted as i.
We occasionally obtained negative integers in equations when using the radican (square root) symbol to solve them. When they realized this, some would halt and respond, "no actual solution," which is technically accurate. We can further simplify radicals by using the imaginary number I which is the square root of real numbers. We occasionally even manage to get rid of the fictitious element, which provides us with actual solutions.
The square root of -1 is the definition of i. A square root is squared to eliminate the two and leave the original number.
To learn more about square visit: https://brainly.com/question/29286039
#SPJ4
In a _______ problem, the objective function line is moved in the direction that reduces cost.
Answers
In a Linear Programming problem, the objective function line is moved in the direction that reduces cost.
Linear Programming (LP) is an operation research approach used to determine the best outcomes, such as optimum profit, minimum cost, or maximum yield, given a set of constraints represented as linear relationships. Linear programming's fundamental idea is to find the best value of a linear objective function that takes into account a variety of constraints that are linear inequalities or equations. The goal of the constraints is to restrict the values of the decision variables. A linear programming problem consists of a linear objective function and linear inequality constraints, as well as decision variables. In a Linear Programming problem, we try to maximize or minimize a linear objective function, which represents our target. This objective function is expressed as a linear equation consisting of decision variables, each of which has a coefficient. Linear programming's ultimate goal is to find values of the decision variables that maximize or minimize the objective function while still satisfying the system of constraints we're working with. In this case, the objective function line is moved in the direction that reduces cost, which means we are minimizing the cost. We do this by moving the objective function line down towards the minimum point. This is the point where the objective function has the smallest possible value that meets all of the constraints.
Thus, in a Linear Programming problem, the objective function line is moved in the direction that reduces cost.
To know more about Linear Programming, click here
https://brainly.com/question/30763902
#SPJ11
1. Which of the following statements is (are) not true about regression model?
A. The intercept coefficient is not typically interpreted.
B. Estimates of the slope are found from sample data.
C. The dependent variable is the explanatory variable.
D. The regression line minimizes the sum of squared errors.
Answers
The correct answer is C. The dependent variable is not typically the explanatory variable in a regression model.
In regression analysis, we aim to understand the relationship between a dependent variable and one or more independent variables. The dependent variable is the variable we are trying to explain or predict, while the independent variables are the ones we use to explain or predict the dependent variable.
In a regression model, the intercept coefficient is typically interpreted. It represents the predicted value of the dependent variable when all the independent variables are equal to zero. So, statement A is not true.
The estimates of the slope coefficients are indeed found from sample data. These coefficients represent the change in the dependent variable associated with a one-unit change in the corresponding independent variable. Therefore, statement B is true.
Finally, the regression line is constructed in a way that it minimizes the sum of squared errors, also known as the residuals. The residuals are the differences between the actual values of the dependent variable and the predicted values from the regression model. So, statement D is true.
In summary, statement C is the only statement that is not true about a regression model. The dependent variable is not typically the explanatory variable in regression analysis.
Know more about regression analysis here,
https://brainly.com/question/33443994
#SPJ11
in the study of vacuum tubes, the equation 0 is encountered. find the taylor polynomial of degree 4 approximating the solution with initial values y(0)1, 0.
Answers
To approximate the solution to equation 0 in the study of vacuum tubes, we can use a Taylor polynomial of degree 4. Given the initial values y(0) = 1 and y'(0) = 0, the Taylor polynomial provides an approximation to the solution based on the values and derivatives at the initial point.
A Taylor polynomial is a polynomial function that approximates a given function by considering its values and derivatives at a specific point. In this case, we are interested in finding an approximation for the solution to the equation 0, given the initial values y(0) = 1 and y'(0) = 0.
To construct the Taylor polynomial of degree 4, we consider the values and derivatives of the function at the initial point x = 0. The polynomial will have terms up to the fourth degree, and the coefficients are determined by the values of the function and its derivatives at x = 0.
The Taylor polynomial of degree 4 can be written as:
y(x) = y(0) + y'(0)x + (y''(0)/2!)x^2 + (y'''(0)/3!)x^3 + (y''''(0)/4!)x^4
Given that y(0) = 1 and y'(0) = 0, we can substitute these values into the polynomial to obtain the specific approximation for the solution.
To learn more about Taylor polynomial click here: brainly.com/question/32073784
#SPJ11
Suppose K is the midpoint of JM. Name a theorem you could use to prove that triangle JKL is congruent to triangle MKL.
Answers
Answer:
i.dk much but try Hypotenuse Leg Theorem very sorry if i wrong so sorry
Step-by-step explanation:
i.dk how i would explain
Answer:
SAS
Step-by-step explanation:
i just got it right