According to the table below, which of these is a possible taxable income for
a married couple filing jointly in the 28% federal income tax bracket?

Answers
Answer: A. $208,850
Step-by-step explanation: took the quiz.
Any taxable income amount falling into one of the tax categories below or above $208,850 would be subject to a different rate of taxation.
Options A) $208,850 is correct.
To determine the possible taxable income for a married couple filing jointly in the 28% federal income tax bracket, we need to find the range of taxable income that falls within the 28% bracket.
Looking at the given table, we can see that the tax brackets are as follows:
Up to $16,700: 10% tax rate
Over $16,700 but not over $67,900: 15% tax rate
Over $67,900 but not over $137,050: 25% tax rate
Over $137,050 but not over $208,850: 28% tax rate
Now, we need to identify the range of taxable income for the 28% tax bracket.
The taxable income range for the 28% bracket is:
Over $137,050 but not over $208,850
So, any taxable income amount that falls within this range will be taxed at a rate of 28%.
For example:
$140,000: This falls within the range of over $137,050 but not over $208,850, so it is a possible taxable income for a married couple filing jointly in the 28% tax bracket.
$200,000: Similarly, this also falls within the same range and is a possible taxable income for the 28% bracket.
Any taxable income amount below $137,050 or above $208,850 would be taxed at a different rate according to the corresponding tax brackets in the table.
So, according to the options A) $208,850 is correct.
Learn more about taxation click;
https://brainly.com/question/22599836
#SPJ3
Related Questions
m(nx^2-y)/z=5n m=6 x=-2 y=-3 z=-5 find n
Answers
0.3673 is the value of the variable n.
The given expression is \(\frac{m(nx^2-y)}{z}=5n\)
First, let's plug the given values into the equation:
\(\frac{6(n2^2-(-3))}{-5}=5n\)
Simplifying:
\(\frac{6(n4+3)}{-5}=5n\\6(4n+3)=-25n\\24n+25n=18\\n=18/49\)
n = 0.3673
Therefore, n is approximately equal to 0.3673.
Learn more about algebraic Expression here:
https://brainly.com/question/953809
#SPJ1
Which is the solution to:
4x– 4 < 10
Answers
Answer:
4x -4 < 10 (add 4 to both sides)
4x < 14 (divide each side by 4)
x < 3.5
Answer:
x< 7/2
Step-by-step explanation:
add for to both sides
divide by four
simplify 14/4
Suppose we want to choose 4 letters, without replacement, from 17 distinct letters. How many ways can this be done, if the order of the choices is not taken into consideration
Answers
Thus, the number of ways in which to choose 4 letters, without replacement, from 17 distinct letters is 57,120.
Define the term permutation?The term permutation applies to a mathematical computation of a number of possible arrangements of a given collection. Simply said, a permutation is a term that defines the amount of different ways something can be organized or arranged.Total distinct letters are 17.
There are 17 alternatives for the initial letter if there are 17 letters.
There are just 16 alternatives left once you remove the letter.
Each time you remove a letter, the bag contains one fewer letter.
Number of ways = 17 x 16 x 15 x 14
Number of ways = 57,120
Thus, if the sequence of the alternatives is irrelevant, there are 57,120 options.
To know more about the permutation, here
https://brainly.com/question/1216161
#SPJ4
The _________________ property of multiplication can be used to group numbers together to make the calculations easier.
Example: (−8.5)(5)(−4) = (−8.5)(−20) = 170
Answers
Answer:
Associative
Step-by-step explanation:
Hope this helped!
Can someone please help I will give brainliest!!! It’s due tonight

Answers
Answer:
1738
Step-by-step explanation:
ya I honestly think that the binomial of the quadriceps and triceratops are
Three persons had dinner in a restaurant. The total bill came to $51.60.
The tip left by them was 25% and was divided equally among them. What was the tip per head
Answers
Answer:
Each person tipped $4.30.
Step-by-step explanation:
We know that the total bill was $51.60. The three people paid a 25% tip, which was split evenly among them.
Since the tip is 25%, it will be 25% of the total. Hence:
\(0.25(51.6) = \$ 12.9\)
The total tip is $12.9.
And since it was evenly split among three people, each person tipped:
\(\displaystyle \frac{12.9}{3}=\$ 4.30\)
Each person tipped $4.30.
Equation 4x - 12 = 12 - 4x
Answers
Answer:
this is infinite solutions
please help me solve this and its about dot plots
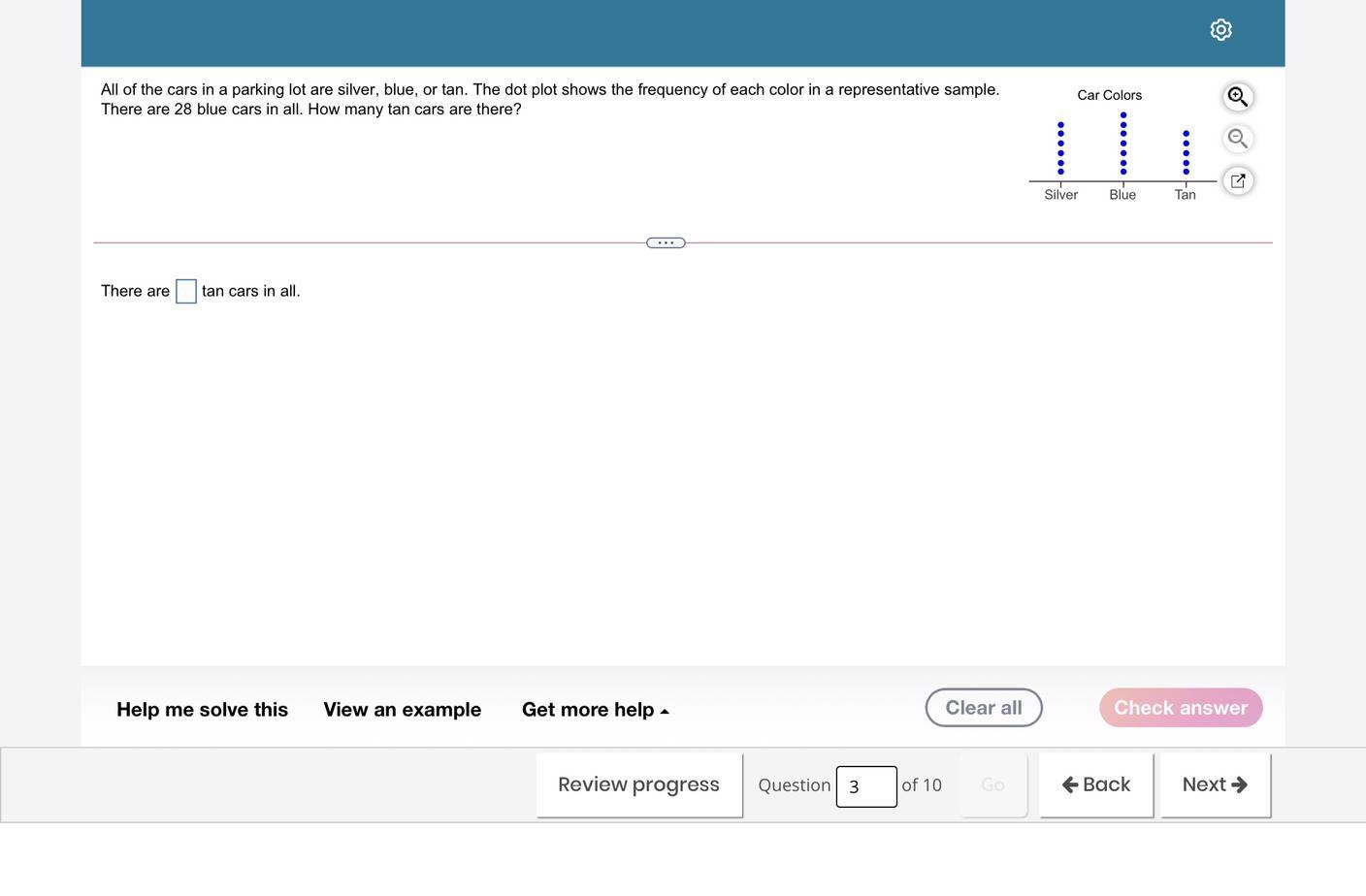
Answers
Answer:
20
Step-by-step explanation:
Number of blue cars = 28
Number of dots in blue cars = 7
one dot = 28÷ 7 = 4
One dot equals 4cars
Number of tan cars = 5*4 = 20
which of the following statements is true n=m n=4m
Answers
Answer:
This statement is true.
Answer:
insufficient info
Step-by-step explanation:
as I see it neither there isn't enough info to find a answer
Raymond is 7.In 3 years,his age will be 5/3 the age of his sister marissa. How old will marissa he in 3 years?
Answers
Answer:
6 years oldStep-by-step explanation:
Raymond is 7His sister is xIn 3 years Raymond will be 10, and his sister x + 3:
10 = 5/3(x + 3)x + 3 = 6x = 3Marissa is 3 now and will be 6 in 3 years
Calcula la diagonal de un rectángulo cuyos lados tienen las siguientes medidas.
a. 5 dm y 4 dm
b. 8 cm y 6 cm
Answers
Las longitudes de las diagonales son √41 dm y 10 cm respectivamente
La medida de la diagonal de un rectángulo: de lado l1 y l2 es igual a
d² = (l1)² + (l2)²
La diagonal entonces es: utilizamos la fórmula dadas para los lados dados y aplicando raíz en la ecuación
A. 5dm y 4dm
d = √((5 dm)² + (4 dm)²) = √(25 + 16) dm = √41 dm
B. 8cm y 6cm
d = √((8 cm)² + (6 cm)²) = √(64 + 36) cm = √100 cm = 10 cm .
A rectangular parking lot measures 3/8 mile by 2/9 mile. Find the area of the parking lot.
Answers
Answer:
1/12 miles
Step-by-step explanation:
Area of rectangular parking lot = length * breadth
Area = 3/8 * 2/9
Area = 6 / 72
Area = 1/12 miles
How can the logarithmic expression be rewritten?
Select True or False for each statement.
(I'm really struggling please help)
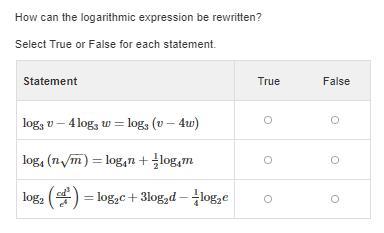
Answers
\(\begin{array}{llll} \textit{logarithm of factors} \\\\ \log_a(xy)\implies \log_a(x)+\log_a(y) \end{array} ~\hspace{4em} \begin{array}{llll} \textit{Logarithm of rationals} \\\\ \log_a\left( \frac{x}{y}\right)\implies \log_a(x)-\log_a(y) \end{array} \\\\\\ \begin{array}{llll} \textit{Logarithm of exponentials} \\\\ \log_a\left( x^b \right)\implies b\cdot \log_a(x) \end{array} \\\\[-0.35em] \rule{34em}{0.25pt}\)\(\log_3(v)-4\log_3(w)\implies \log_3(v)-\log_3(w^4)\implies \log_3\left( \cfrac{v}{w^4} \right) \\\\[-0.35em] ~\dotfill\\\\ \log_4(n\sqrt{m})\implies \log_4(n)+\log_4(\sqrt{m}) \\\\\\ \log_4(n)+\log_4\left( m^{\frac{1}{2}} \right) \implies \log_4(n)+\cfrac{1}{2}\log_4(m)~~\textit{\large \checkmark} \\\\[-0.35em] ~\dotfill\\\\ \log_2\left( \cfrac{cd^3}{e^4} \right)\implies \underline{\log_2(cd^3)}-\log_2(e^4) \\\\\\ \underline{\log_2(c)+\log_2(d^3)}-\log_2(e^4) \implies \log_2(c)+3\log_2(d)-4\log_2(e)\)
Let X be a random variable with expected value 3 and variance 5. According to the Chebyshev inequality, P(|X - 3I greaterthanorequalto 0.44) lessthanorequalto (give your answer to six decimal places)
Answers
The upper bound of the probability is P(|X - 3| ≥ 0.44) ≤ 5 / 0.44^2 ≈ 32.37e-2.
By the Chebyshev inequality, for any positive number k, we have:
P(|X - E[X]| ≥ k) ≤ Var[X] / k^2
In this case, we want to find P(|X - 3| ≥ 0.44), which is equivalent to P(X - 3 ≥ 0.44 or X - 3 ≤ -0.44). So we choose k = 0.44 and use the inequality:
P(|X - 3| ≥ 0.44) ≤ Var[X] / 0.44^2
Substituting Var[X] = 5 and solving for the upper bound of the probability, we get:
P(|X - 3| ≥ 0.44) ≤ 5 / 0.44^2 ≈ 32.37e-2
Rounding to six decimal places, we have:
P(|X - 3| ≥ 0.44) ≤ 0.323666
Learn more about probability here
https://brainly.com/question/13604758
#SPJ11
Write as a fraction in lowest terms:

Answers
Answer:
\(\frac{79}{100}\)
Step-by-step explanation:
Question:
Write as a fraction in lowest terms:
Answer:
a = 79
b = 99
the chance of getting a rare disease is .03 per person. out of 1,000 people, how many of them are expected to get the disease?
Answers
Answer:
I believe the answer would be 30 people.
Step-by-step explanation:
To calculate the percentage out of a group of people or items, you just multiply the percent (in decimal form) by the amount of people you want it out of. For example: A 0.1% chance out of 1,000 people would be a chance and expectancy of 1 person out of those 1,000 people. In this case it's 3% for every person. 0.03 • 1,000 is 30.
Do the ratios 2/3 and 12/18 form a proportion?
yes
no
Answers
Answer:
Yes
Step-by-step explanation:
Because 12/18 = 2/3..(cancel 12 and 18 by 6)
Answer:
yes
Step-by-step explanation:
2x6=12
3x6=18
6 is the multiplying number
( the 2 equations are the same amount )
A triangle has two sides of length 1 and 4. What is the largest possible whole-number length
for the third side?
Answers
Using the triangle inequality theorem, the largest possible whole-number length for the third side is 4.
How to Apply the Triangle Inequality Theorem to Find the Length of the Third Side of a Triangle?The third side of a triangle must be shorter than the sum of the other two sides and longer than the difference between the other two sides.
So, for a triangle with sides of length 1, 4, and x (where x is the length of the third side), we have:
1 + 4 > x
4 + x > 1
1 + x > 4
Simplifying these inequalities, we get:
5 > x
x > 3
x > -3 (this inequality is always true)
The largest possible whole-number length for the third side is 4, since it is the largest integer that satisfies the above inequalities.
Learn more about the triangle inequality theorem on:
https://brainly.com/question/309896
#SPJ1
Find the volume of the solid generated by revolving the region bounded by the graphs of
y sex, y >= 0 and x >= 0 about the x-axis.
Answers
The volume of the solid generated by revolving the region bounded by the graphs of y = x, y ≥ 0, and x ≥ 0 about the x-axis is 0 cubic units.
To find the volume using the disk method, we integrate the cross-sectional areas of the disks formed by revolving the region about the x-axis. The region bounded by y = x and y = 0 represents the area under the curve y = x in the positive x-axis region.
The radius of each disk is given by the value of y, which is equal to x in this case. The volume of each disk can be expressed as dV = πx^2 * dx.To determine the limits of integration, we consider the x-values where the curves intersect. In this case, y = x intersects y = 0 at the origin (0, 0). Therefore, the integral for the volume is V = ∫(0 to c) πx^2 * dx, where c represents the x-value where the curves intersect.
Evaluating the integral, we have V = π∫(0 to c) x^2 * dx. Integrating x^2 with respect to x gives V = π * [x^3/3] evaluated from 0 to c. Since c represents the x-value where the curves intersect, we have c = 0. Substituting the limits of integration, the volume simplifies to V = π * (0^3/3 - 0^3/3) = 0.
Therefore, the volume of the solid generated by revolving the region bounded by the graphs of y = x, y ≥ 0, and x ≥ 0 about the x-axis is 0 cubic units.
Learn more about volume here
https://brainly.com/question/32619305
#SPJ11
Which FAR Part 77 imaginary surface has slopes that may range from 20:1 to 50:1?
The primary surface
The horizontal surface
The approach surface
The conical surface
Answers
The conical surface is the correct answer as it allows for slopes ranging from 20:1 to 50:1. The FAR Part 77 imaginary surface that has slopes that may range from 20:1 to 50:1 is the conical surface.
The conical surface is a three-dimensional surface defined by a combination of horizontal and inclined planes. It extends upward and outward from the end of the primary surface and has varying slope requirements. The slope of the conical surface represents the ratio of the change in elevation to the horizontal distance. A slope of 20:1 indicates that for every 20 units of horizontal distance, there is a 1-unit increase in elevation.
Similarly, a slope of 50:1 means that for every 50 units of horizontal distance, there is a 1-unit increase in elevation. Therefore, the conical surface is the correct answer as it allows for slopes ranging from 20:1 to 50:1.
To learn more about conical surface click here: brainly.com/question/29129362
#SPJ11
what quadrant is point D located in?quadrant lquadrant llquadrant lllquadrant lV

Answers
The point D is located in quadrant iii. Here we have (-, -)
Please help me solve this question

Answers
Answer:
The number must also be a multiple of 4,2,1
Step-by-step explanation:
To find the missing number, we need to find the factors of 8
8 = 4*2*1
The number must also be a multiple of 4,2,1
Answer:
1, 2 and 4 (in increasing order)
Step-by-step explanation:
Your number must also be a multiple of 1 (which every single number is), 2 (every even number is a multiple of 8, since 8 is even, it's a multiple of 2), and 4.
Let's think about the factors of 8, or numbers that you can divide evenly into 8 and get a natural number.
These are:
1
2
4
So these three are the numbers that your number's a multiple of.
Learn more;work harder
#Carryonlearning
=============================================================
You may need to use the appropriate appendix table or technology to answer this question.
A population has a mean of 800 and a standard deviation of 200. Suppose a sample of size 400 is selected and
x
is used to estimate μ. (Round your answers to four decimal places.)
(a)____
What is the probability that the sample mean will be within ±5 of the population mean?
(b)___
What is the probability that the sample mean will be within ±10 of the population mean?
Answers
a. The probability that the sample mean will be within ±5 of the population mean is the area under the normal curve between these two z-scores. b. The lower bound z-score is (-10 - 0) / 10 = -1, and the upper bound z-score is (10 - 0) / 10 = 1. We can use the same normal distribution table or technology to find the probability associated with these z-scores.
(a) To find the probability that the sample mean will be within ±5 of the population mean, we can use the Central Limit Theorem (CLT) and the properties of a normal distribution.
The sample mean, is an unbiased estimator of the population mean, μ. According to the CLT, the distribution of sample means approaches a normal distribution with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
= 200 / √400
= 200 / 20
= 10
To find the probability that the sample mean will be within ±5 of the population mean, we can standardize the interval using the z-score:
For the lower bound (-5), the z-score is (-5 - 0) / 10 = -0.5.
For the upper bound (+5), the z-score is (5 - 0) / 10 = 0.5.
We can now use a standard normal distribution table or technology (such as a calculator or statistical software) to find the probability associated with the z-scores -0.5 and 0.5. The probability that the sample mean will be within ±5 of the population mean is the area under the normal curve between these two z-scores.
(b) To find the probability that the sample mean will be within ±10 of the population mean, we follow the same steps as in part (a).
The lower bound z-score is (-10 - 0) / 10 = -1, and the upper bound z-score is (10 - 0) / 10 = 1. We can use the same normal distribution table or technology to find the probability associated with these z-scores.
Note: Since the question mentions rounding answers to four decimal places, please use the appropriate table or technology to obtain the precise probabilities for parts (a) and (b).
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
please help me with this maths question

Answers
The asked net for the cube of side length 2 cm has been shown.
What is surface area?The surface area is defined as a region of any shape is the area of the shape that is faced or the Surface area is the amount of area covering the exterior of a 3D shape.
Here,
The cube of side length 2 cm is given we have to draw the net for the given cube.
So first we calculate the surface area,
surface area of the cube = 6 [a]²
surface area = 6 (2)² = 24 cm²
Here, as the cube has 6 faces, unbind the cube on the coordinate plate.
Thus. the required net for the cube has been shown.
Learn more about the surface area here: https://brainly.com/question/2835293
#SPJ1

Find the measure of each angle supplementary angles with measures 2X +3 and 3X +2
Answers
supplementary angles = the sum of those angles will equal to 180 degrees
so,
2x + 3 + 3x + 2 = 180
5x + 5 = 180
5x = 175
x = 35
angle 1 -> 2x + 3 = 70 + 3 = 73
angle 2 -> 3x + 2 = 105 + 2 = 107
if you want to check, 107 + 73 = 180
hope it helps :)
HELP QUICK PLEASE!!!
8. Calculate the return on investment in dollars and as a percentage for an investment that you purchase for $500 and sell for $600. TIP: If you don't remember how to calculate return on investment, review the Calculating ROI pages in Section 4, Lesson 2.
Answers
Answer:
100
Step-by-step explanation:
PLEASE HELP ME!!!!!!! VERY CONFUSED AND I NEED THIS VERY BADLY!!!!!! I appreciate the help!!!!

Answers
Answer:
exact form: x= 2/3, -4 decimal form:x= 0.6 , -4
Step-by-step explanation:
I’m confused on what number 4 means. Can someone please help?

Answers
Answer:I think you can say like the most bought music in class B is alternative and the lowest one is classical and so on
Step-by-step explanation:
FIND df/ds
f = xy^2 + yz^2 + + xsinz in the direction of A= i2 + j(-1) +k2
Answers
The direction derivative of A is \(\frac{df}{ds}= 2y^2+2sinz-2xy+4yz+2xcosz\).
Given that
\(f = xy^2 + yz^2 + + xsinz\) in the direction of A= 2i + -j+2k.
To find the \(\frac{df}{ds}\) = ∇f · A, of vector A= 2i + -j+2k.
Where ∇f is the gradient of f and (·) represents the dot product.
Let's us calculate ∇f:
∇f = \(\frac{∂f}{∂x}i + \frac{∂f}{∂y}j +\frac{∂f}{∂z}k.\)
Differentiate partially with respect to each variable, we have:
\(\frac{ ∂f}{∂x} = y^2 + sinz\)
\(\frac{∂f}{∂y}= 2xy\)
\(\frac{∂f}{∂z}= 2yz + xcosz\)
Therefore, ∇f is:
∇\(f = (y^2 + sinz)i + (2xy)j + (2yz + xcosz)k.\)
Now, the dot product of ∇f and A:
∇f · A = \((y^2 + sinz)(2) + (2xy)(-1) + (2yz + xcosz)(2).\)
∇f · A = \(2y^2 + 2sinz - 2xy + 4yz + 2xcosz.\)
Hence, the directional derivative of f in the direction of A is:
\(\frac{df}{ds}= 2y^2+2sinz-2xy+4yz+2xcosz\)
Learn more about Gradient here:
https://brainly.com/question/30301793
#SPJ4
The specifications for a plastic liner for a concrete highway project calls for thickness of 4.0 mm±0.10 mm. The standard deviation of the process is estimated to be 0.02 mm. The upper specification limit for this product =mm (round your response to three decimal places). The upper specification limit for this product = 4.1 mm (round your response to three decimal places). The lower specification limit for this product = 3.9 mm (round your response to three decimal places). The process is known to operate at a mean thickness of 4.0 mm. The process capability index (Cpk)= 1.667 (round your response to three decimal places). The upper specification limit lies about 5 standard deviations from the centerline (mean thickness).
Answers
The lower specification limit (LSL) for the plastic liner is 3.9 mm (rounded to three decimal places).
To calculate the upper specification limit (USL) for the plastic liner, we know that it lies about 5 standard deviations (σ) from the centerline or mean thickness. The process has a mean thickness of 4.0 mm and a standard deviation (σ) of 0.02 mm.
So, the USL can be calculated as follows:
USL = Mean + (5 * σ)
= 4.0 mm + (5 * 0.02 mm)
= 4.0 mm + 0.1 mm
= 4.1 mm
Therefore, the upper specification limit (USL) for the plastic liner in this highway project is 4.1 mm (rounded to three decimal places).
Similarly, the lower specification limit (LSL) can be calculated by subtracting 5 standard deviations from the mean thickness:
LSL = Mean - (5 * σ)
= 4.0 mm - (5 * 0.02 mm)
= 4.0 mm - 0.1 mm
= 3.9 mm
Therefore, the lower specification limit (LSL) for the plastic liner is 3.9 mm (rounded to three decimal places).
It's worth noting that the given information also mentions the process capability index (Cpk), which is a measure of how well the process meets the specifications. In this case, the Cpk is calculated as (USL - Mean) / (3 * σ), and it is determined to be 1.667 (rounded to three decimal places).
Learn more about decimal from
https://brainly.com/question/28393353
#SPJ11