Algebra 2 - Grade 11
Can anyone please help me soon as possible?
Use synthetic substitution to find f(–3) and f(4) for each function.
f(x) = x^2 – 5x + 10
f(x) = x^3 + 3x^2 + 2x – 50
Answers
Answer:
for the first equation
f(-3) = 34
f(4) = 6
for the 2nd equation
f(-3) = -56
f(4) ÷ 70
Step-by-step explanation:
my work is attached in a picture.
all you do is substitute each x value into each equation
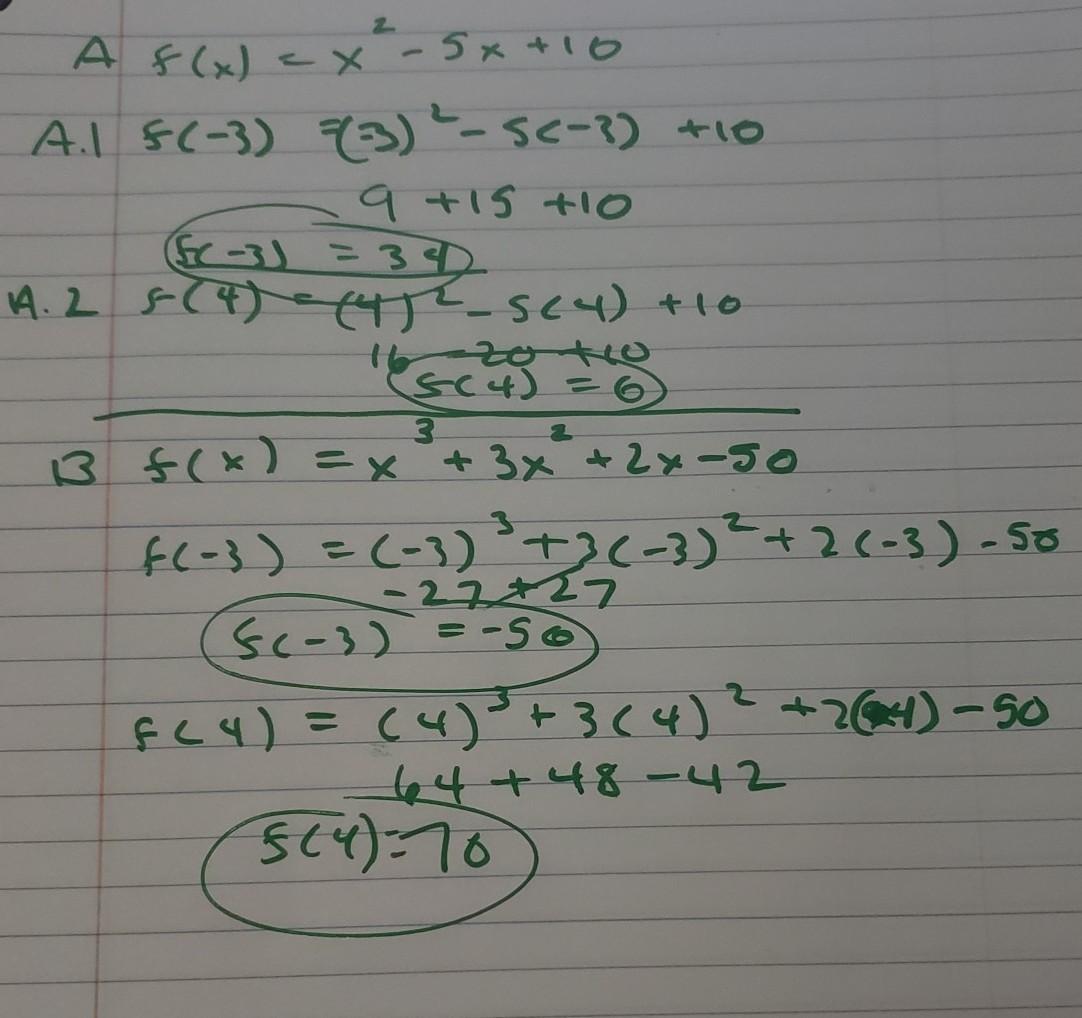
Related Questions
Graph linear equations

Answers
Answer:
(3,-6)(1,-4)=9
Step-by-step explanation:
8) (3,-6) (1,-4)
so (3,-6)(1,-4) = 9
hope this is correct! :)
11. The function f(t) = 40 sin (π/45 t) +48 models the height in feet of one car od a Ferris wheel called the Colossus, where t is the time in seconds. Each of the functions below models the motion of a different Ferris wheel. Which Ferris wheel has the same diameter as The Colossus?
a. g(t) = 40 cos (π/45 t) +50
b. h(t) = 39 cos (π/60 t) + 49
c. j(t) = 39 sin (π/45 t) + 48
d. k(t) = 39 sin (π/45 t) + 49
Answers
Ferris wheel has the same diameter as The Colossus is g(t) = 40 cos (π/45 t) +50. So, correct option is A.
To determine which of the given functions represents a Ferris wheel with the same diameter as The Colossus, we need to use the fact that the diameter of a Ferris wheel is equal to the amplitude of the sinusoidal function that models its height.
The amplitude of the function f(t) = 40 sin (π/45 t) +48 is 40, so the diameter of The Colossus is 40 feet. We need to find the function that also has an amplitude of 40.
Looking at the given answer choices, we see that function g(t) has an amplitude of 40 cos (π/45 t) +50, which is equal to 40. This means that the Ferris wheel represented by function g(t) has a diameter of 40 feet, the same as The Colossus.
Functions h(t), j(t), and k(t) all have amplitudes that are less than 40, so they represent Ferris wheels with smaller diameters than The Colossus.
Therefore, the answer is A.
To learn more about function click on,
https://brainly.com/question/31910278
#SPJ1
In your own words, how can you solve this equation?

Answers
Answer:
a square + b square = c square
Campbells wants to try and sell their soup in boxes rather than cans. The original cans have a height of 6 inches and a diameter of 4 inches. If the boxes can only be 2 inches deep, 4 inches wide and the keep the volume the same, what is the height of the new rectangular box
Answers
To find the height of the new rectangular box, we first need to determine the volume of the original can. The can has a height of 6 inches and a diameter of 4 inches, which means it has a radius of 2 inches. The volume of a cylinder (can) is calculated using the formula V = πr²h.
In this case, V = π(2²)(6) = 24π cubic inches.
Now, we need to find the height of the new rectangular box that has a width of 4 inches and a depth of 2 inches. To maintain the same volume, the formula for the volume of a rectangular prism (box) is V = lwh.
Since we know the volume (24π cubic inches), width (4 inches), and depth (2 inches), we can solve for the height (h):
24π = (4)(2)(h)
24π = 8h
Now, divide both sides by 8:
h = 3π inches
So, the height of the new rectangular box would be 3π inches to maintain the same volume as the original can.
To know more about volume visit:
https://brainly.com/question/1578538
#SPJ11
All of the following are equivalent, except_
x(2+1)
3x
2x2
2X+X
Answers
3x = 3x
2x^2 = 2x^2
2x+x = 3x
Options 1, 2, and 4 all simplify down to 3x while Option 3 does not. Therefore, the answer is 2x^2
The equation of the ellipse that has a center at ( 3 , 1 ) (3,1), a focus at ( 7 , 1 ) (7,1), and a vertex at ( − 2 , 1 ) (-2,1), is ( x − C ) 2 A 2 + ( y − D ) 2 B 2 = 1 (x-C)2A2+(y-D)2B2=1
Where:
A=
B=
C=
D=
Answers
The equation of the ellipse with a center at (3, 1), a focus at (7, 1), and a vertex at (-2, 1) is given by \(\(\frac{{(x - 3)^2}}{{36}} + \frac{{(y - 1)^2}}{{25}} = 1\).\). In this equation, A = 6, B = 5, C = 3, and D = 1.
To find the equation of the ellipse, we need to determine the values of A, B, C, and D in the general form equation \(\[\frac{{(x - C)^2}}{{A^2}} + \frac{{(y - D)^2}}{{B^2}} = 1\]\)for an ellipse. The center of the ellipse is (C, D), so C = 3 and D = 1.
The distance between the center and each focus is given by the value of A, so we can calculate A as the distance between (3, 1) and (7, 1), which is 4. Therefore, A = 4.
The distance between the center and each vertex is given by the value of B, so we can calculate B as the distance between (3, 1) and (-2, 1), which is 5. Hence, B = 5. Plugging these values into the general form equation, we get \(\(\frac{{(x - 3)^2}}{{36}} + \frac{{(y - 1)^2}}{{25}} = 1\)\) as the equation of the ellipse.
Learn more about equation of ellipse here:
https://brainly.com/question/30995389
#SPJ11
Joan has started a physical fitness program. One of her goals is to be able to run at least 5
miles without stopping. She can now run 3.5 miles without stopping. How many more
miles must she run non-stop to achieve her goal?
Answers
Answer:
1.5 miles
Step-by-step explanation:
Since Joan need to run 5 miles without stopping and already runs 3.5 miles without stopping, the number of miles more she must run non-stop to achieve her goal of 5 miles without stopping is the difference between her 5 mile goal and her current run of 3.5 miles.
So, number of miles she must run = 5 miles - 3.5 miles = 1.5 miles.
So, Joan must run 1.5 miles more non-stop to achieve her goal.
The graph below shows how much Hailey’s plane is climbing in how many seconds. How much is she climbing each second

Answers
Answer:
The answer is 48
Step-by-step explanation:
Just take one of the points shown in the graph and in this case x is the seconds the plane has being flying up and the y values is how much the plane is climbing. So, divide your x and y values to get your slope so its 192/4 and simplified is 48/1 or 48 per second
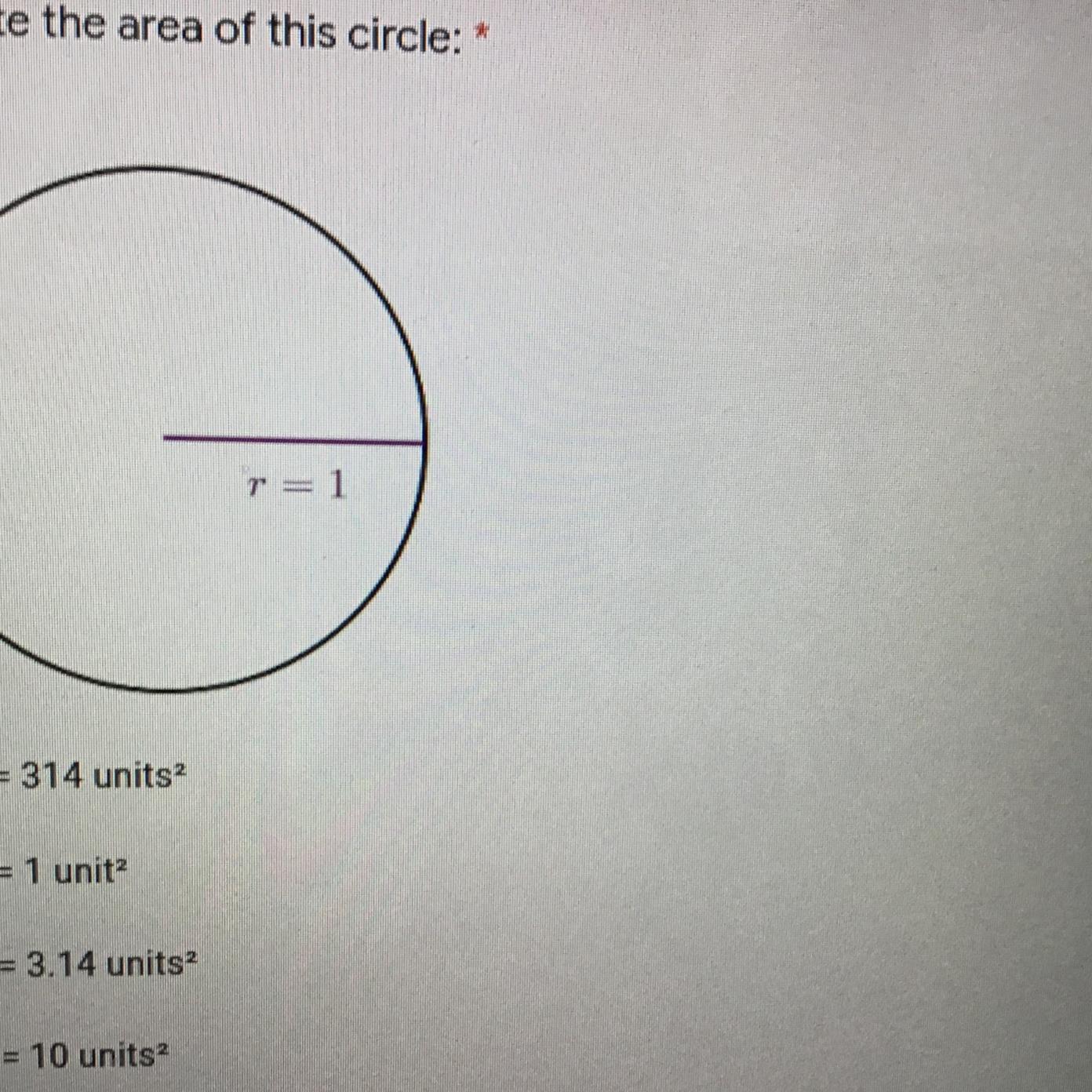
Please help! (Calculate the area of this circle)
Answers
Answer:
10 units hope this helps!!!!!!!
Step-by-step explanation:
Martina needs to make a total of 40 deliveries this week. so far she has completed 12 of them. what percentage of her total deliveries has Martina completed??? pls help
Answers
Answer: 10 percent
Step-by-step explanation:
because she was supposed to do 40 she did only 12 so it is 10%
Find the measure of

Answers
=======================================================
Explanation:
The angles SPT and TPU marked in red are congruent. They are congruent because of the similar arc markings.
Those angles add to the other angles to form a full 360 degree circle.
Let x be the measure of angle SPT and angle TPU.
86 + 154 + 60 + x + x = 360
300 + 2x = 360
2x = 360-300
2x = 60
x = 60/2
x = 30
Each red angle is 30 degrees.
Then,
angle SPQ = (angle SPT) + (angle TPU) + (angle UPQ)
angle SPQ = (30) + (30) + (86)
angle SPQ = 146 degrees
--------------
Another approach:
Notice that angles QPR and RPS add to 154+60 = 214 degrees, which is the piece just next to angle SPQ. Subtract from 360 to get:
360 - 214 = 146 degrees
What is the measure of x? *
X
80°
180 degrees
100 degrees
80 degrees
360 degrees

Answers
Answer: 80 degrees
Step-by-step explanation:
Answer:
80 degrees!
Step-by-step explanation:
There's this weird phenomenon with parallel lines, that if you trace a line over it, you would get the same angle on the opposite side of the line.
Se realiza un viaje en avión desde una ciudad A a una ciudad C, haciendo escala en un aeropuerto ubicado en la cuidad B, en el primer aeropuerto se bajan la mitad de los pasajeros, en su segunda parada llegando a su destino se bajan 1/3 pasajeros, la cantidad de pasajeros que quedan en el avión serán
Answers
Answer:
La cantidad de pasajeros que quedan en el avión serán \(\frac{1}{6}\)
Step-by-step explanation:
Sabes que en el primer aeropuerto se bajan la mitad de los pasajeros, es decir que se bajan \(\frac{1}{2}\) pasajeros, y en la segunda parada llegando a destino se bajan \(\frac{1}{3}\) pasajeros. Entonces, la cantidad de pasajeros que se bajan en ambas paradas es la suma de la cantidad de pasajeros que se bajaron entre el primer y segundo aeropuerto:
\(\frac{1}{2}+\frac{1}{3}\)
Lo primero que debes hacer es hayar un denominador común entre el 2 y el 3. Para eso, hallas el mínimo común múltiplo entre ambos, en este caso 6.
Luego debes multiplicar cada numerador por el número que hayas multiplicado el denominador. Para ello, dividis este mínimo común múltiplo entre el denominador inicial, y este resultado se multiplica por el numerador de esa fracción. De esta manera se obtiene:
\(\frac{1}{2}+\frac{1}{3}=\frac{3}{6} +\frac{2}{6}\)
Finalmente se suman los numeradores y se obtiene:
\(\frac{1}{2}+\frac{1}{3}=\frac{5}{6}\)
Considerando que 1 es un entero que representa la cantidad de total de pasajeros, para calcular la cantidad de pasajeros que quedan en el avión se realiza la sustracción:
\(1-\frac{5}{6}\)
Resolviendo de manera similar a la suma, se obtiene:
\(1-\frac{5}{6}=\frac{6}{6} -\frac{5}{6}\)
\(1-\frac{5}{6}=\frac{1}{6}\)
Entonces la cantidad de pasajeros que quedan en el avión serán \(\frac{1}{6}\)
a market sells five kinds of cups, 4 kinds of saucers, and 2 kinds of spoons. How many ways are there to buy two objects of different types? WILL GIVE BRAINLIST
Answers
Answer:
Step-by-step explanation:
To solve this problem, we need to determine the number of ways to choose two objects of different types from the given sets.
We can start by computing the number of ways to select two objects from each of the three sets, and then add these numbers together. Since we must choose two different types, we cannot choose two objects from the same set.
The number of ways to choose two cups is:
C(5,2) = 5! / (2! * (5-2)!) = 10
The number of ways to choose two saucers is:
C(4,2) = 4! / (2! * (4-2)!) = 6
The number of ways to choose two spoons is:
C(2,2) = 1
Since we must choose two different types, we need to multiply the number of ways to choose two objects from different sets. There are three sets to choose from, so we need to choose two of them as follows:
3 choices of sets * number of ways to choose two objects from each set = 3 * (10 + 6 + 1) = 51
Therefore, there are 51 ways to buy two objects of different types from the given sets of cups, saucers, and spoons.
What is 3/4 as a percentage?
Answers
Answer:
75%
Hope this helps!!!
Step-by-step explanation:
Answer:
0.75
Step-by-step explanation:
Imagine four quarters, 1 quarter equals 25 cents. So adding 2 more quarters, 3 total, would equal 75 cents. 25 + 25 + 25 = 75. Your answer is 0.75! Hope this helps!
Edit: MY BAD!! I THOUGHT YOU SAID DECIMAL, IGNORE ME!!!
solve by substitute. 9y+8=x. -2x+8y=-36
Answers
Answer:
Let's solve for x.
9y+8=x
Step 1: Flip the equation.
x=9y+8
Answer:
x=9y+8
Let's solve for x.
−2x+8y=−36
Step 1: Add -8y to both sides.
−2x + 8y + −8y = −36 + −8y
−2x = −8y − 36
Step 2: Divide both sides by -2.
−2x / −2 = −8y − 36 / −2
x=4y + 18
Answer:
x=4y + 18
Hope it helps
Please mark me as the brainliest
Thank you
Answer:
(26, 2)
x = 26
y = 2
Step-by-step explanation:
Given:
9y + 8 = x
-2x + 8y = -36
Substitute (9y + 8) for x in the second equation.
-2(9y + 8) + 8y = -36
Then distribute and solve.
-18y + (-16) + 8y = -36
Combine like terms.
-10y - 16 = -36
-10y = -20
y = 2
Solve for x by substituting the y value (2) into 9y + 8 = x.
9(2) + 8 = x
18 + 8 = x
x = 26
Therefore, the solution is (26, 2) in terms of (x, y).
PLEASE HELP!!! I GIVE TONS OF POINTS!!! THANKSSS!!!! IM GIVING 100 POINTS OR MORE FOR THIS PROBLEM!!!!!!!! YOU WILL BE MARKED BRAINLIEST!!!!
In a survey of 229 professional athletes, it was found that 99 of them owned a convertible, 84 of them owned a giant screen TV, and 98 owned a sporting goods store. 16 owned a convertible and a store, 26 owned a TV and a store, and 41 owned a covertible and a TV. 5 owned all three items.
How many athletes did not own any of the three items?_____________
How many owned a covertible and a TV, but not a store?____________
How many athletes owned a convertible or a TV?_________________
How many athletes owned exactly one type of item in the survey?___________
How many athletes owned at least one type of item in the survey?__________
How many owned a TV or a store, but not a convertible?___________
Answers
Answer:
Hope that this is helpful.
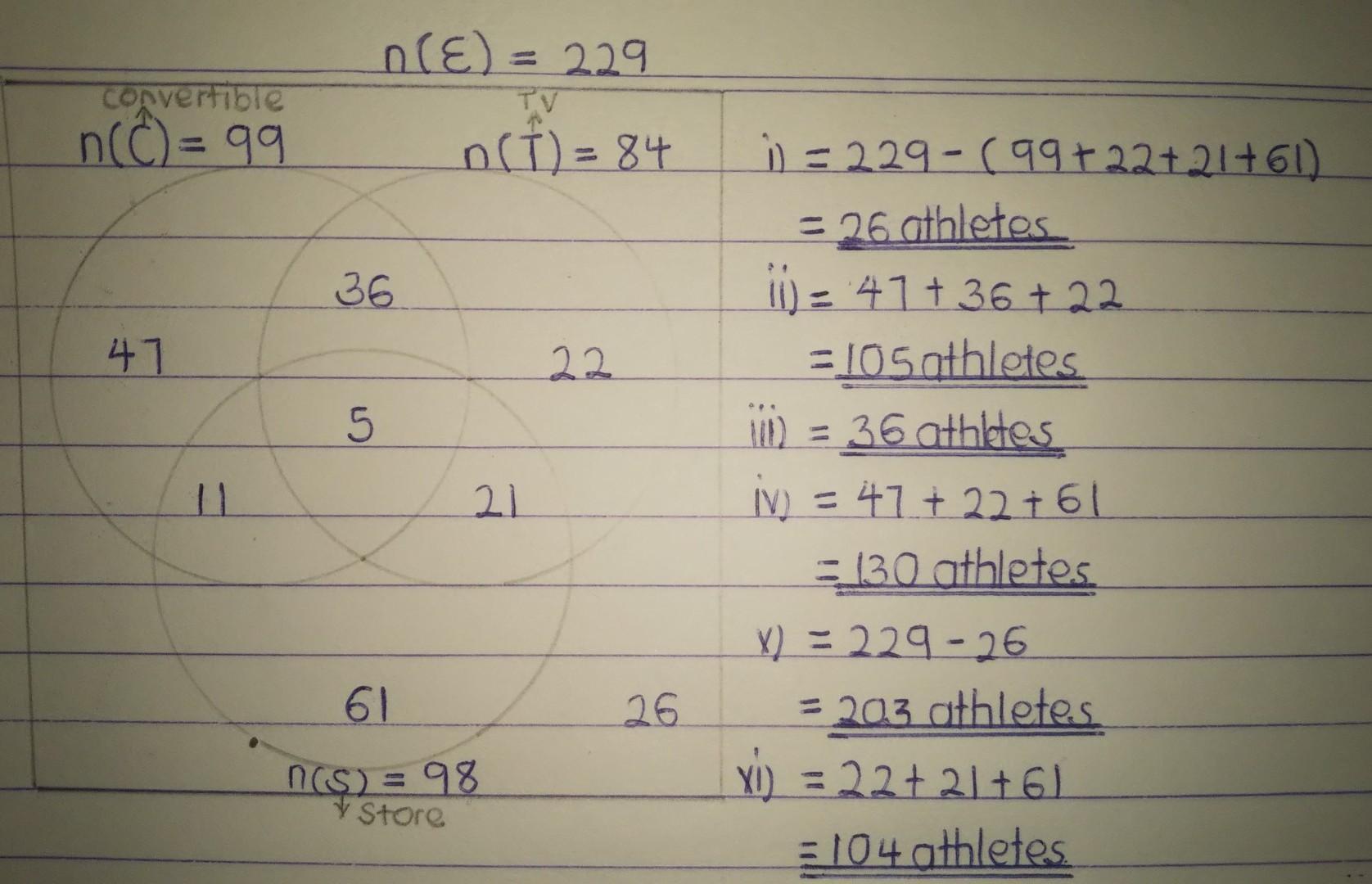
A triangle has vertices at $(-3,2),(6,-2),(3,5)$. How many square units are in the area of the triangle
Answers
The area of the triangle is 19.5 square units.
To find the area of the triangle, we can use the formula:
Area = (1/2) * base * height
where the base and height are the distance between two of the vertices of the triangle. We can choose any two vertices to use as the base and height, as long as we use the same units for both. Let's choose (-3,2) and (6,-2) as our base.
The distance between (-3,2) and (6,-2) can be found using the distance formula:
d = \(\sqrt((6 - (-3))^2 + (-2 - 2)^2)\)
d = \(\sqrt(81 + 16)\)
d = \(\sqrt(97)\)
Now we need to find the height of the triangle. The height is the perpendicular distance from the third vertex (3,5) to the line containing the base (-3,2) and (6,-2). We can use the formula:
height = \(|Ax + By + C| / \sqrt(A^2 + B^2)\)
where A, B, and C are the coefficients of the line in the standard form Ax + By + C = 0, and x and y are the coordinates of the third vertex. We can find the coefficients of the line by using the two points (-3,2) and (6,-2):
A = 2 - (-2) = 4
B = (-3) - 6 = -9
C = 6*(-2) - (-3)*2 = -18
Now we can plug in the values to find the height:
height = \(|4*3 - 9*5 - 18| / \sqrt(4^2 + (-9)^2)\)
height = \(39 / \sqrt(97)\)
Finally, we can plug in the base and height to find the area:
Area = \((1/2) * \sqrt(97) * (39 / \sqrt(97))\)
Area = 19.5
Therefore, the area of the triangle is 19.5 square units.
To know more about area, refer to the link below:
https://brainly.com/question/21107816#
#SPJ11
To search for in-depth science content, visitAdult tickets to the fall play cost and student tickets cost . The drama class sold more student tickets than adult tickets to the fall play. If the class collected from ticket sales, how many student tickets were sold
Answers
If the class collected $660 from ticket sales, the drama class sold a total of 90 student tickets. Let's assume that the number of adult tickets sold is x.
Since the drama class sold 25 more student tickets than adult tickets, the number of student tickets sold can be expressed as (x + 25).
The total revenue from ticket sales is given as $660. Adult tickets cost $6 each and student tickets cost $3 each. Therefore, the total revenue can be expressed as 6x + 3(x + 25).
Setting up the equation: 6x + 3(x + 25) = 660.
Simplifying the equation: 6x + 3x + 75 = 660.
Combining like terms: 9x + 75 = 660.
Subtracting 75 from both sides: 9x = 585.
Dividing both sides by 9: x = 65.
Therefore, the drama class sold 65 adult tickets.
To find the number of student tickets sold, we substitute the value of x into the expression (x + 25): (65 + 25) = 90.
Thus, the drama class sold 90 student tickets.
Learn more about expression here:
https://brainly.com/question/28170201
#SPJ11
At a sale, dresses were sold for $76 each. If the dresses originally cost $200 each,
what percentage of its original price was a dress sold for?
Answers
The percentage of dress was sold for 62% of its original price.
To find the percentage of the original price that the dress was sold for, we can use the formula for percentage change:
Percentage Change = (Change in Value / Original Value) × 100
In this case, the original value is the cost of the dress ($200), and the change in value is the difference between the original cost and the sale price ($76):
Original Value = $200
Sale Price = $76
Change in Value = Original Value - Sale Price
Change in Value = $200 - $76
Change in Value = $124
Now we can plug these values into the percentage change formula:
Percentage Change = (Change in Value / Original Value) ×100
Percentage Change = ($124 / $200) × 100
Percentage Change = 0.62× 100
Percentage Change = 62%
To know more about percentage here
https://brainly.com/question/32197511
#SPJ3
A student graphs the function f (x) = 2(4)* using a graphing calculator. The student then replaces the 2 in the equation with an 8.
Which best describes the change the student sees when graphing the new function?
O The graph of the new function will be vertically shifted up 4 units when compared to the previously graphed function.
O The graph of the new function will be vertically shifted up 6 units when compared to the previously graphed function.
O The graph of the new function will be vertically stretched by a factor of 4 when compared to the previously graphed function.
O The graph of the new function will be vertically stretched by a factor of 6 when compared to the previously graphed function.
Answers
The equation will be changed into = f(x)= 32
What are equations?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
We have LHS = RHS (left hand side = right hand side) in every mathematical equation.
To determine the value of an unknown variable that represents an unknown quantity, equations can be solved.
A statement is not an equation if it has no "equal to" sign.
A mathematical statement called an equation includes the sign "equal to" between two expressions with equal values.
Hence, The equation will be changed into = f(x)= 32
learn more about equations click here:
brainly.com/question/2972832
#SPJ1
use hardy-weinberg formula to evaluate the following. the frequency of disease xyz is about 1/4300. what is the probability that a mother a carrier?
Answers
The probability that a mother is a carrier is approximately 0.018.
The Hardy-Weinberg equilibrium formula can be used to determine the frequency of alleles in a population, as well as to make predictions about the probability of certain traits occurring in the next generation. In this case, we are interested in determining the probability that a mother is a carrier of a particular disease, given that the frequency of the disease is 1/4300.
To use the Hardy-Weinberg formula, we need to know the frequency of both the dominant and recessive alleles in the population. Assuming that the disease allele is recessive (i.e., carriers are heterozygous), we can represent the frequency of the disease allele (q) as
\(q = \sqrt{(1/4300)} = 0.004644.\)
To determine the frequency of carriers (heterozygotes), we can use the formula p * q * 2,
where p represents the frequency of the dominant allele (which is equal to 1 - q in this case).
Therefore:
\(p = 1 - q \\ = 1 - 0.004644 = 0.995356\\q = \sqrt{(1/4300} = 0.004644\\p * q * 2 =0.018\)
Approximately 1.8% of the population will be carriers of the disease allele. This means that the probability that a mother is a carrier is approximately 0.018.
You can learn more about probability at
https://brainly.com/question/24756209
#SPJ11
a) determine an equation for the family of quartic functions with zeroes -5/2, -1, 7/2, 3.
b) write equations for two functions that belong to this family
c) determine an equation for the member of the family whose graph passes through the point (-2,25)
Answers
a. A quartic function with zeroes -5/2, -1, 7/2, and 3 can be written as
f(x) = a(x + 5/2)(x + 1)(x - 7/2)(x - 3), b) Two examples of functions that belong to this family are: f1(x) = 2(x + 5/2)(x + 1)(x - 7/2)(x - 3)
f2(x) = -0.5(x + 5/2)(x + 1)(x - 7/2)(x - 3) and the equation for the member of the family that passes through the point (-2,25) is:
f(x) = (4/275)(x + 5/2)(x + 1)(x - 7/2)(x - 3)
What is quadratic equation?
it's a second-degree quadratic equation which is an algebraic equation in x.
a) A quartic function with zeroes -5/2, -1, 7/2, and 3 can be written as the product of linear factors with those zeroes:
f(x) = a(x + 5/2)(x + 1)(x - 7/2)(x - 3)
where "a" is a constant that determines the overall scaling of the function.
b) Two examples of functions that belong to this family are:
f1(x) = 2(x + 5/2)(x + 1)(x - 7/2)(x - 3)
f2(x) = -0.5(x + 5/2)(x + 1)(x - 7/2)(x - 3)
Note that these functions differ only in the value of the constant "a".
c) To find the value of "a" that makes the graph of the function pass through the point (-2,25), we can substitute x = -2 and y = 25 into the equation for f(x):
25 = a(-2 + 5/2)(-2 + 1)(-2 - 7/2)(-2 - 3)
Simplifying this expression:
25 = a(5/2)(-1)(-11/2)(-5)
25 = a(6875/4)
a = 100/6875 = 4/275
Therefore, the equation for the member of the family that passes through the point (-2,25) is:
f(x) = (4/275)(x + 5/2)(x + 1)(x - 7/2)(x - 3)
To learn more about quadratic equation from the given link:
brainly.com/question/30098550
#SPJ1
Suppose that (X, d, T) is a discrete dynamical system and X is finite. Prove that (X, d, T) has a periodic point.
Answers
The discrete dynamical system (X, d, T) has a periodic point, which is x.
To prove that a discrete dynamical system (X, d, T) with finite X has a periodic point, follow these steps:
1. Since X is finite, there is a finite number of elements in X. Let's say there are N elements in X.
2. Consider applying the transformation T to an arbitrary point x in X. Since T is a function from X to X, the result of applying T to x will also be in X. In other words, T(x) is also an element of X.
3. Now, apply the transformation T repeatedly to x. We will obtain a sequence of points x, \(T(x), T^2(x), T^3(x), ..., T^N(x),\)where \(T^n(x)\) means applying T n times to x.
Since there are N elements in X and we have applied T N times, by the pigeonhole principle, there must be at least one point that repeats in the sequence.
4. Let's say \(T^i(x) = T^j(x)\) for some i < j. Then, \(T^i(T^{j-i}(x)) = T^j(T^{j-i}(x))\), and we can apply \(T^{j-i}\) to both sides of the equation, which gives \(T^i(x) = T^j(x).\)
5. This shows that x has a period of (j-i). Thus, the discrete dynamical system (X, d, T) has a periodic point, which is x.
for such more question on dynamical system
https://brainly.com/question/30408733
#SPJ11
WILL GIVE BRAINLIEST!!
A line has a slope of 1/3 and passes through the point (–9, –3). What is its equation in slope-intercept form?
Answers
Answer:
y = \(\frac{1}{3}\) x
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
here slope m = \(\frac{1}{3}\) , then
y = \(\frac{1}{3}\) x + c ← is the partial equation
to find c substitute (- 9, - 3) , that is x = - 9, y = - 3 into the partial equation
- 3 = \(\frac{1}{3}\) (- 9) + c = - 3 + c ( add 3 to both sides )
0 = c
y = \(\frac{1}{3}\) x + 0 , that is
y = \(\frac{1}{3}\) x
The pair of triangles that are congruent by the ASA criterion i:
The pair of triangles that are congruent by the SAS criterion is
Answers
Step-by-step explanation:
The pair of triangles that are congruent by the SAS criterion is Δ BAC and ΔRQP.hope this helps
Clare sketches a rectangular prism with a height of 11 and a square base and labels the edges of the base LaTeX: 8. She asks Han what he thinks will happen to the volume of the rectangular prism if she triples LaTeX: 8. Han says the volume will be 9 times bigger. Is he right? Explain or show your reasoning.
Answers
The volume will be 9 times increased if she triples the dimension of the square. So, yes, he is right because 3 is 2 times in the formula.
What is Geometry?It deals with the size of geometry, region, and density of the different forms both 2D and 3D.
Given
Clare sketches a rectangular prism with a height of 11 and a square base and labels the edges of the base 8.
The side of the square is 8.
The height of the prism is 11.
Volume = Area of square × height.
The volume of the original prism will be.
\(\rm V_1 = 8 * 8 * 11\\\\V_1 = 704\)
If she triples the side of the square.
Then dimensions will be
The side of the square is 24.
The height of the prism is 11.
The volume of the modified prism will be.
\(\rm V_2 = 24 * 24* 11\\\\V_2 = 9*704\\\\V_2 = 9 \ Times \ of \ V_1\)
Thus, the volume will be 9 times bigger. So, yes, he is right because 3 is 2 times in the formula.
More about the geometry link is given below.
https://brainly.com/question/7558603
What is the slope of the line in the graph?
-4/3
-3/4
3/4
4/3

Answers
Answer: -3/4
Step-by-step explanation: I'M SMART
Which ONE of the following is the correct way to write a confidence interval? In the answer choices below, L represents the lower bound of the confidence interval and U represents the upper bound of the confidence interval. O [LU] O [LU) O (UL) O (UL) O (LU) O (UL) O (UL) O (LU) O (UL) O (LU)
Answers
The correct way to write a confidence interval is an option [LU]
Confidence interval:A confidence interval is typically written as [lower bound, upper bound], where the square brackets indicate that the bounds are included in the interval.
For example, a 95% confidence interval for a population mean might be written as [15.2, 20.8]. This means that we are 95% confident that the true population mean lies between 15.2 and 20.8.
In the answer choices, option (O [LU]) is the correct way to write a confidence interval because it follows this convention of using square brackets to indicate the inclusion of the bounds.
Option (O [LU)) uses a parenthesis for the upper bound, which could be confusing since parentheses typically indicate exclusion.
Options (O (UL)) and (O (UL)) switch the order of the bounds, which would be incorrect since the lower bound should come first.
The other options either use parentheses instead of brackets or reverse the order of the bounds, which are both incorrect.
Therefore,
The correct way to write a confidence interval is an option [LU]
Learn more at Confidence intervals at
https://brainly.com/question/24131141
#SPJ4
How do you use the binomial theorem to expand the expression (x + y)^4?
Answers
We establish the given binomial expression (x + y)^4 in the following way
What is binomial theorem in simple terms?The nth power of the sum of two integers a and b may be represented as the sum of n + 1 terms of the form, according to the binomial theorem, which states that for every positive integer n.
What is a binomial equation in math?A polynomial with just terms is a binomial. An illustration of a binomial is x + 2, where x and 2 are two distinct words. Additionally, in this case, x has a coefficient of 1, an exponent of 1, and a constant of 2. As a result, a binomial is a two-term algebraic statement that comprises a constant, exponents, a variable, and a coefficient.
(x+y) 4=
((x+y)2) 2=
(x2+2xy+y2) 2=
(x2+2xy) 2+2(x2+2xy) (y2)+(y2) 2=
(x4+4x3y+4x2y2)+(2x2y2+4xy3)+(y4)=
x4+4x3y+6x2y2+4xy3+y4
The binomal theorem is a more comprehensive strategy:
(x+y)
n=∑k=0n(nk)
⋅xn−k⋅yk=∑k=0n(nk)
⋅xk⋅yn−k\sWhere\s(nk)=n!((n−k)!)⋅(k!)
n!={1n⋅((n−1)!)
n=0n>0
∑k=0nf(k)=f(0)+f(1)+f(2)+…+f(n)
To learn more about binomial theorem, click the following link:-
https://brainly.com/question/13672615
#SPJ1