An aeroplane covers a distance of 1500km in a certain time at a certain speed.After increasing the speed by 100km/hr, it covers the same distance in a time which is half an hour less than the previous time. Find the previous speed of the aeroplane.
this is from quadratic equations CBSE grade 10
please answer ASAP
Answers
Answer: U = 600 m/s
Step-by-step explanation:
Given that an aeroplane covers a distance of 1500km in a certain time t at a certain speed U.
After increasing the speed by 100km/hr, that is, V = U + 100 it covers the same distance in a time which is half an hour less than the previous time. That is t2 = t - 0.5.
From the first statement
Speed = distance/ time
Distance = speed × time
1500 = Ut
Make t the subject of the formula
t = 1500/U ..... (1)
From the second statement
Distance = speed × time
1500 = (U + 100) × ( t - 0.5 )
Open the bracket
1500 = Ut - 0.5U + 100t - 50
Collect the like terms
1550 = Ut - 0.5U + 100t .... (2)
Substitutes equation 1 into 2
1550 = 1500U/U - 0.5U + 100(1500/U)
1550 = 1500 - 0.5U + 150000/U
1550 - 1500 = (150000 - 0.5U^2)/U
Cross multiply
50U = 150000 - 0.5U^2
0.5U^2 + 50U - 150000 = 0
Divide all by 0.5
U^2 + 100U - 300000 = 0
Using completing the square method
U^2 + 100U = 300000
U^2 + 100U + 50^2 = 300000 + 50^2
(U + 50)^2 = 302500
U + 50 = sqrt(302500)
U + 50 = +/-(550)
U = 50 + 550 or 50 - 550
U = 600 or - 500
Since U is of the same direction, it is
positive. Therefore, the previous speed of the aeroplane is 600 m/s
Answer:
500km/hr
Step-by-step explanation:
The formula for Speed (km/hr) = Distance / Time
Where S = Speed
D = Distance
T = Time
S = D/T
From the question, the aeroplane covered a distance of 1500 km
S = 1500/ T
ST = 1500
Time taken( T ) = 1500/S ......... Equation 1
We are told from the question that speed was increases by 100km/hr, it covers the same distance in a time which is half an hour less than the previous time
This is expressed mathematically as:
The new speed =S + 100km/hr
The new Time taken = 1500/ S - 1/2....... Equation 2
Also since Time = Distance / Speed
The new Time taken also = 1500/ S + 100 ......... Equation 3
Step 1
We would simplify Equation 2:
Time = 1500/S - 1/2
Find the Lowest common multiple = 2
Time = (2 × 1500 - S )/ 2S
Time = 3000 - S / 2S ......... Equation 4
Step 2
Equate Equation 4 and 3 together since they are both equal to time taken
1500/ S + 100 = 3000 - S / 2S
We cross multiply
2S × 1500 = (S + 100) ( 3000 - S)
3000S = 3000S - S² + 300000 - 100S
3000S - 3000S + S² - 300000 + 100S = 0
S² + 100S - 300000 = 0
Step 3
We solve for S = Speed by using factorisation method.
S² + 100x - 300000 = 0
S² - 500S + 600S - 300000 = 0
(S² - 500S) + (600S - 300000) = 0
S(S - 500) + 600(S - 500) = 0
(S - 500) (S + 600) = 0
S - 500 = 0, S = 500
S + 600 = 0 , S = -600
Our answer cannot be in negative form, hence, the previous speed of the aeroplane = 500km/hr
Related Questions
Which expression is equivalent to this polynomial?
9x^2 + 4
A. (3x + 2i)(3x − 2i)
B. (3x + 2)(3x − 2)
C. (3x + 2i)^2
D. (3x + 2)^2
Answer: A. (3x + 2i)(3x − 2i)
I hope this helps.
Answers
Answer:
A is the answer.
Step-by-step explanation:
In the first, we must know i^2 is (-1)
so we can get the answer is A.
A.(3x + 2i)(3x − 2i)
= (3x)^2 - (2i)^2
= 9x^2 + 4 (Answer)
B. (3x + 2)(3x − 2) = 9x^2 - 4
C. (3x + 2i)^2
= 9x^2 + 12ix - 4
D. (3x + 2)^2
= 9x^2 + 12x + 4
Simplify: (x + 7)(x-4)
A. 2r +3
B. 12-28
C. x2-3x - 28
D. x2 + 3x - 28
Answers
Answer:
(x + 7)(x - 4) = x2 - 4x + 7x - 28 = x2 + 3x - 28
Mr. Randall, a salesperson, earns a weekly salary of $300 plus a commission of 7% of
his weekly sales of merchandise. Last week, Mr. Randall earned $426. This can be
represented by the equation below, where s represents his total sales, in dollars, for
the week.
$300 + $0.07s = $426
How many dollars worth of merchandise did Mr. Randall sell last week?
Answers
Answer:
-3
Step-by-step explanation:
Based on his weekly salary and commission, we can calculate that Mr. Randall sold goods worth $1,800.
In the formula given, sales is represented as s. To find the total sales, you can solve the equation:
300 + 0.07s = 426
0.07s = 426 - 300
s = 126 / 0.07
= $1,800
In conclusion, Mr. Randall sold $1,800 worth of goods.
Find out more at https://brainly.com/question/19297414.
Use a calculator to find the approximate value of the expression Round the answer to two decimal places 4 sec 13 sec 4 13 1.8 (Round to two decimal places as needed)
Answers
The approximate value of the expression sec 4π / 13 is 1.76
Radian is a unit of measurement of angles equal to about 57.3° . equivalent to angle subtended at the center of a circle by a arc equal to length of radius
To Change Radian into degree, we multiple the angle with 180/π
The given Expression is
sec 4π / 13
Changing radian into Degree ,
=> 4π / 13 × 180 / π
=> 720 / 13
=> 55.38
Therefore , sec 55.38° is 1.7603
rounding off to two decimal places is 1.76
To know more about Radian here
https://brainly.com/question/7721249
#SPJ4
I need help with this

Answers
By applying Pythagoras' theorem, the length of x is equal to 10 units.
How to calculate the length of x?In Mathematics and Geometry, Pythagorean's theorem is modeled or represented by the following mathematical equation (formula):
x² + y² = z²
Where:
x, y, and z represents the length of sides or side lengths of any right-angled triangle.
Based on the information provided about the side lengths of this right-angled triangle, we have the following equation:
x² = y² + z²
x² = 8² + 6²
x² = 64 + 36
x = √100
x = 10 units.
Read more on Pythagorean theorem here: brainly.com/question/15430861
#SPJ1
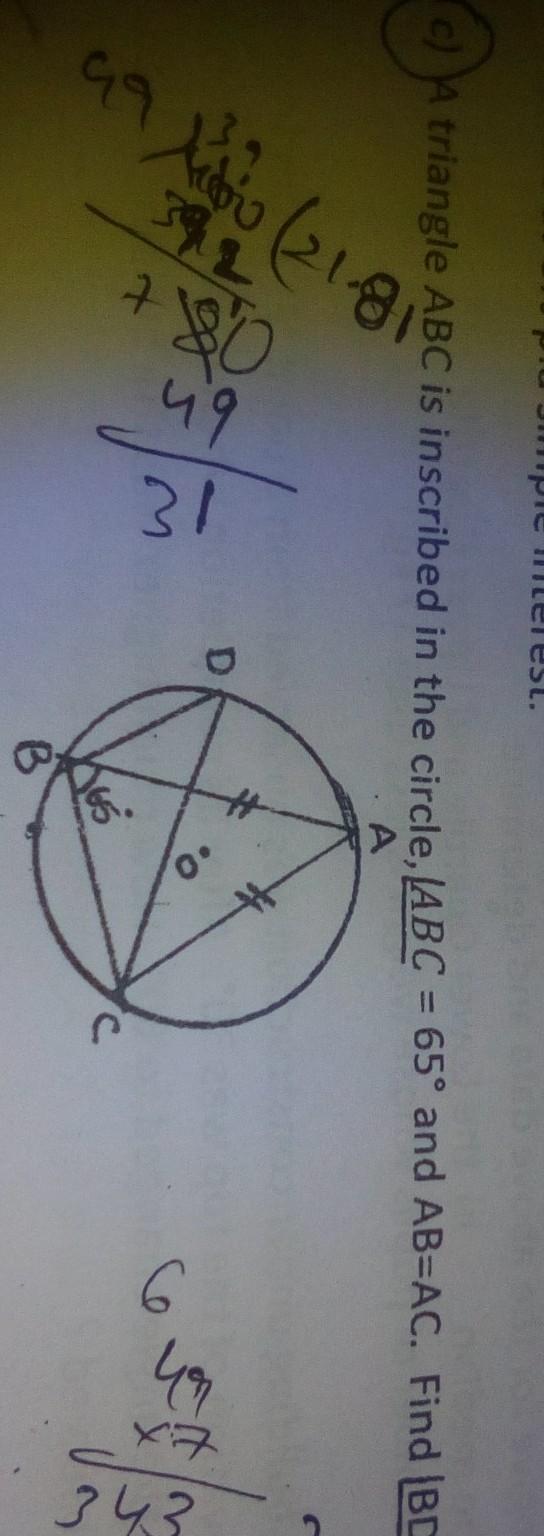
A triangle ABC is inscribed in the circle, (ABC = 65° and AB=AC. Find (BDC.
A
aado (218
h
7
.
4
343
Answers
Answer:
∠BDC=50°
Step-by-step explanation:
∠BDC=∠A[angles at the same segment)
∠A= 180-(65+65)=180-130= 50°
so, ∠BDC=50°
MARK ME BRAINLIEST
The value of angle BDC would be,
⇒ ∠BDC = 50°
What is mean by Angle?An angle is a combination of two rays (half-lines) with a common endpoint. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle.
Since, We know that;
∠BDC = ∠A
By angles at the same segment.
Here, We have;
⇒ ∠A = 180-(65+65)
⇒ ∠A = 180-130
⇒ ∠A = 50°
Thus, The value of angle BDC would be,
⇒ ∠BDC = 50°
Learn more about the angle visit:;
https://brainly.com/question/25716982
#SPJ2
Rachael gave a survey to her classmates to learn about their superstitions. Here's some of the data she collected.
can you answer the one in the picture and this question also please:
This data set contains:Choose 1 Answer:
A) 4 Variables, 1 of which is quantitative
B) 4 variables, 2 of which are quantitative
C) 3 variables, 1 of which is quantitative
D) 3 variables, 2 of which are quantitative

Answers
The individuals in this data set are B) Rachael's Classmates
The first column of the table is what will give this away
==========================================================
This data set contains A) 4 Variables, 1 of which is quantitative
Why is this? Because the four variables are
GenderAgeBirth monthRead horoscopeAge is quantitative because it deals with a quantity or number. We can do things like find the average age and it makes sense to do so. The other variables are qualitative or categorical. Gender is nominal as you can't order the data. Birth month is ordinal though because we can order the months from January to December. The responses for "read horoscope" are nominal data because we cannot order "yes" versus "no".
If segment AB is 4 units, segment AD is 23 units, and segment CD is 12 units, what is the length of segment BC?
23
A
9 units
B.
6 units
C
7 units
D
8 units
Answers
Answer:
C . 7 unitsStep-by-step explanation:
The question is lacking appropriate diagram. Find the diagram to the question attached.
From the diagram, it can be seen that AD = AB+BC+CD
Given the following
AD = 23units
AB = 4units
CD = 12units
To get C=BC, we will substitute the given segments into the expression above as shown;
23 = 4+BC+12
23 = BC + 4 + 12
23 = BC+16
Subtract 16 from both sides
23-16 = BC+16-16
7 = BC
Hence the length of segment BC is 7units.

Solve each trigonometric function IN THE INTERVAL [0, 2)
3 sec2x − 2 tan2x − 4 = 0
Answers
The intersection of the graph is (0.65, 1.073). Then the solution of the equation the interval of [0, 2) will be 0.65.
What is the solution to the equation?The allocation of weights to the important variables that produce the calculation's optimum is referred to as a direct consequence.
The trigonometric function is given below.
3 sec2x − 2 tan 2x − 4 = 0
Simplify the equation, then we have
3 sec2x − 2 tan 2x − 4 = 0
3 / cos 2x − 2 sin 2x / cos 2x = 4
3 − 2 sin 2x = 4 cos 2x
(3 − 2sin 2x)² = 16 cos² 2x
The graph of the functions is drawn below.
From the graph, the intersection of the graph is (0.65, 1.073). Then the solution of the equation the interval of [0, 2) will be 0.65.
More about the solution of the equation link is given below.
https://brainly.com/question/545403
#SPJ1

What is the additive inverse of (7x – 20)?
Answers
Answer:
cannot factor.
Step-by-step explanation:
Diff of squares help me out
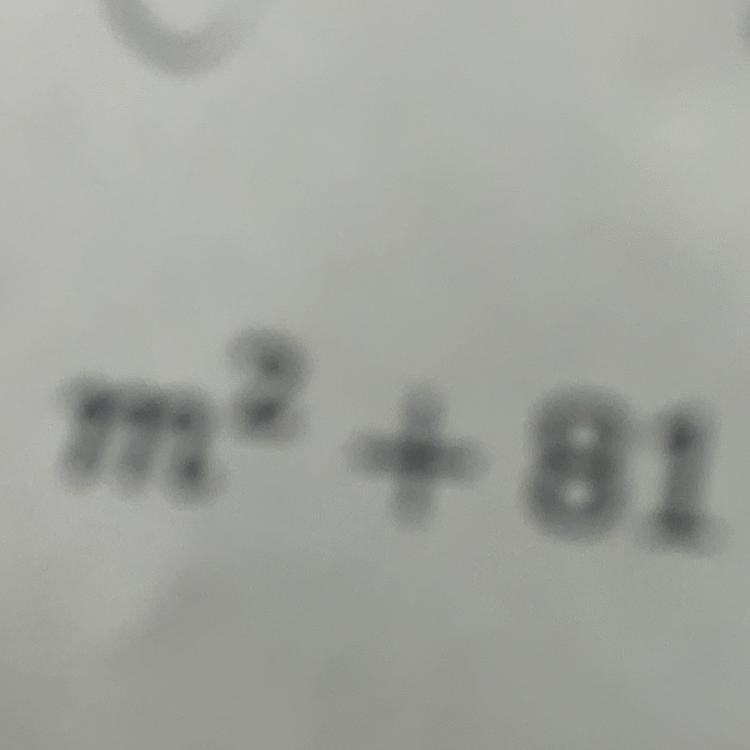
Answers
Answer:
9
Step-by-step explanation:
9 is the correct answer
Please help ineed this to pass 42 points if solved

Answers
The area of the rectangle as a product of length and width is (6x² + 13x + 6) square units
What is an equation?An equation is an expression that shows the relationship between numbers and variables.
The area of a rectangle is the product of its length and its width. It is given by:
Area = length * width
From the diagram:
Area = 6(x²) + 13(x) + 6(1) = 6x² + 13x + 6 square unit
Also:
Length = x + x + x + 1 + 1 = 3x + 2
Length = 3x + 2 units
Width = x + x + 1 + 1 + 1 = 2x + 3
Width = 2x + 3 units
Area = length * width
Substituting:
Area = (3x + 2)(2x + 3)
Area = 6x² + 9x + 4x + 6 = 6x² + 13x + 6 square units
The area is (6x² + 13x + 6) square units
Find out more on equations at: https://brainly.com/question/2972832
#SPJ1
Solve -2a - 5>3
Which graph shows the solutions?

Answers
-4>3
Step-by-step explanation:
Answer:
First line
Step-by-step explanation:
Isolating 2a is the first step, so adding 5 to each side. That leaves -2a > 8. Divide both sides by -2, and because it's a negative, you flip the sign. so you get a < -4
12. DIG DEEPER The sum of a three-digit
number and a one-digit number is 731.
The product of the numbers is 2,908,
What are the numbers?
Answers
The three digit number is 727 while the one digit number is 4
Given data
The sum of a three-digit number and a one-digit number is 731.
The product of the numbers is 2,908
How to solve for the numberslet three digit number be x, y, and z
let the one digit be w
The sum
xyz + w =731
xyz * w = 2,908
making xyz the subject of formula
xyz = 731 - w
plugging in xyz into xyz * w = 2,908
( 731 - w ) * w = 2908
731w - w^2 = 2908
w^2 - 731w + 2908 = 0
solving the quadratic equation gives
w = 727 or 4
since w is a one digit number then w = 4
plugging in w = 4 into xyz + w =731 we have
xyz + w =731
xyz + 4 =731
xyz =731 - 4
xyz = 727
Hence the three digit number is 727 while the one digit number is 4
Read more word problems on here: https://brainly.com/question/13818690
#SPJ1
I NEED HELP ASAPPP PLEASEEEE!!!!
Second bulb: When 3 is the input, the output is _____. When 10 is the input, the output is _______.
Answers
When 3 is the input, the output is 10. When 10 is the input, the output is 15.
How to explain the informationIt should be noted that the input for the function is time, measured in hours. The output of the function is energy usage, measured in kilo watts.
From the information, the energy usage of a light bulb is a function. The input for the function is time measured in hours. The output of the function is energy usage, measured in Kilo watts. E (energy) is a function of t (time).
The graph of the function will show energy usage on the y axis and time on the x axis.
Learn more about energy on:
https://brainly.com/question/11577594
#SPJ1
A tunnel for an amusement park ride has the shape of a
regular hexagonal prism with dimensions shown. The prism
has a volume of 3,572.1 cubic meters. Can two 8-meter cars
connected by a 3-meter connector pass through the tunnel
at the same time? Explain.
Answers
The 3,572.1 m³ volume of the hexagon and the 19 m. length of the cars and 3-m connector, gives;
Yes, two cars connected by a 3 meter connector can pass through the tunnel at the same timeHow can the capacity of the tunnel be found?From a similar question, we have;
Side length of the hexagon = 8.1 m
Perpendicular distance from the center to a side of the hexagon = 7 m.
Therefore;
Cross sectional area of the hexagon, A is found as follows;
A = 6 × 0.5 × 7 × 8.1 = 170.1
Length of the tunnel, D = 3572.1 ÷ 170.1 = 21
D = 21 meters
Length of two cars and a connector, L = 8 + 8 + 3 = 19
The tunnel length, D = 21 m. is longer than the length of two cars and the connector, L = 19 m.
Therefore;
Two cars connected by a 3 meter connector can pass through the tunnel at the same time.Learn more about the volume of a prism here;
https://brainly.com/question/8976947
Find the transfer function from a reference input θr to the Hapkit output θ for the closed-loop system when the Hapkit (the plant) is placed in a unity gain negative feedback with a PID controller. How many poles does the closed loop system have?
Answers
The denominator has a single first-order term the closed-loop system has a single pole at:
s = -G(s) × (Kp + Kd × s) / Ki
The transfer function from the reference input θr to the Hapkit output θ for a closed-loop system with a unity gain negative feedback and a PID controller can be derived as follows:
Let's denote the transfer function of the plant (Hapkit) by G(s) the transfer function of the PID controller by C(s) and the transfer function of the feedback path by H(s).
The closed-loop transfer function T(s) is given by:
T(s) = θ(s) / θr(s)
= G(s) × C(s) / [1 + G(s) × C(s) × H(s)]
Since the feedback path has unity gain we have H(s) = 1.
Also, the transfer function of a PID controller with proportional gain Kp, integral gain Ki and derivative gain Kd is:
C(s) = Kp + Ki/s + Kd × s
Substituting these into the expression for T(s), we get:
T(s) = θ(s) / θr(s)
= G(s) × [Kp + Ki/s + Kds] / [1 + G(s) × [Kp + Ki/s + Kds]]
Multiplying both the numerator and denominator by s, and simplifying, we get:
T(s) = θ(s) / θr(s)
= G(s) × Kps / [s + G(s) × (Kp + Ki/s + Kds)]
This is the transfer function from the reference input θr to the Hapkit output θ for the closed-loop system.
The closed-loop system has as many poles as the order of the denominator of the transfer function T(s).
Since the denominator has a single first-order term the closed-loop system has a single pole at:
s = -G(s) × (Kp + Kd × s) / Ki
The pole may change as a function of the frequency s due to the frequency dependence of G(s).
For similar questions on closed-loop system
https://brainly.com/question/14289243
#SPJ11
a^2-2ab-36b^2 factorize
Answers
The expression a² - 2ab - 36b², can be factorize as: (a - 6b)^2.
How to Factorize a Polynomial Expression?The polynomial expression a² - 2ab - 36b² can be factored as shown below:
This is done by finding two numbers that multiply to -36 and add to -2ab. The numbers are -6b and 6b, and the expression can be written as:
(a - 6b)(a - 6b), which can be simplified to (a - 6b)^2.
Therefore, given the polynomial expression, a² - 2ab - 36b², when factorized, we would get (a - 6b)².
Learn more about factorization on:
https://brainly.com/question/25829061
#SPJ1
can someone please answer the first four for me? Also can someone please explain it to me, because I don't fully understand

Answers
The function A() given by A()=0. 24551 can be ued to etimate the average age of employee of a company in the year 1981 to 2009. Let A() be the average age of an employee, and be the number of year ince 1981; that i, =0 for 1981 and =9 for 1990. What wa the average age of the employee in 2003 and in 2009?
Answers
The the function to estimate the average age of employee of a company is A(s)=0.285s + 59 , then the average age of employee in 2003 is 65.27 and in 2009 is 66.98
To estimate the average age of an employee in 2003, we need to find the value of A(s) when s = 22 ;
because the number of years between 2003 and 1981 is = 22 years ;
So , A(22) = 0.285×22 + 59 = 65.27 ;
The average age of an employee in 2003 is approximately 65.27.
To estimate the average age of an employee in 2009,
we need to find the value of A(s) when s = 28
because the number of years between 2009 and 1981 is = 28 years ;
So , A(28) = 0.285×28 + 59 = 66.98 ;
The Average age of employee in 2009 is approximately 71.48.
The given question is incomplete , the complete question is
The function A(s) given by A(s)=0.285s + 59 can be used to estimate the average age of employee of a company in the year 1981 to 2009. Let A(s) be the average age of an employee, and "s" be the number of year since 1981; that is, s=0 for 1981 and s=9 for 1990. What is the average age of the employee in 2003 and in 2009 ?
Learn more about Function here
https://brainly.com/question/14909799
#SPJ4
After 4 years, $20,000 deposited in a savings account with simple interest had earned $800 in interest. What was the interest rate?
Answers
The interest rate for the savings account is 5% after 4 years, $20,000 deposited in a savings account with simple interest earned $800 in interest.
We can use the formula for simple interest to solve the problem:
Simple interest = (Principal * Rate * Time) / 100
where Principal is the initial amount deposited, Rate is the interest rate, and Time is the time period for which the interest is calculated.
We know that the Principal is $20,000 and the time period is 4 years. We are also given that the interest earned is $800. So we can plug in these values and solve for the interest rate:
$800 = (20,000 * Rate * 4) / 100
Multiplying both sides by 100 and dividing by 20,000 * 4, we get:
Rate = $800 / (20,000 * 4 / 100) = 0.05 or 5%
Therefore, the interest rate for the savings account is 5%.
To know more about interest here
https://brainly.com/question/25720319
#SPJ4
A steel plate (50×50×0.5 cm ^3
) is to be cast using the sand casting process. If the liquid shrinkage of the steel during solidification is 3%, calculate the following (3. Volume of motten metal required to avoid shrinkage b. Calculate the dimension of a cubical riser to avoid shrinkage c. Check the adequacy of the riser using Cain's method
Answers
For the steel plate which is to be cast,
The volume of molten metal required to avoid shrinking is about 1289mL.
The dimensions of a cubical riser, which can avoid shrinkage are 3.38cm.
The riser's adequacy cannot be proved.
This question is based on the basic principles of metallurgy.
A)
We calculate the volume of molten metal which is required to avoid shrinkage after accounting for the shrinkage which will occur.
So, the volume of metal required for final casting is:
Final Casting Volume (F.C.V) = Initial volume / (1 - Shrinkage)
The value of shrinkage is in decimals.
Here, the steel liquid shrinks by 3% during solidification.
Inital volume = 50*50*0.5
= 1250 cm³
So,
F.C.V = 1250/(1 - 0.03)
F.C.V = 1250/0.97
F.C.V = 1288.6 cm³
So, about 1289 mL of liquid steel is required to avoid shrinkage.
B)
If we need the riser to compensate for the shrinkage, we need it to provide enough metal while it solidifies.
So, Riser Volume = Shrinkage Volume
Shrinkage Volume (S.V) = (F.C.V)*(Shrinkage)
= 1288.6(0.03)
= 38.65 cm³
But since we need the dimensions,
Dimensions = ∛(S.V) (Cubical Riser)
= ∛(38.65)
= 3.38 cm
The dimension of the cubical riser is 3.38 cm.
C)
According to Cain's Rule, the volume of the riser is more than or equal to 1.5 times the volume of casting that it is intended to feed.
Without the casting volume, we cannot prove its adequacy.
For more on Casting Process,
brainly.com/question/31181282
#SPJ4
b. Notice that two sides and a nonincluded angle of ΔABC are congruent to the corresponding parts of ΔABD , but the triangles are not congruent. Must ΔEFG be congruent to ΔABD if E F=10, F G=6 , and ∠ E≅∠ A ? Explain.
Answers
Based on the given information, ΔEFG is not necessarily congruent to ΔABD, even though EF is congruent to AB, FG is congruent to BD, and ∠E is congruent to ∠A. Additional information is needed to determine the congruence of the two triangles.
In order to determine congruence between triangles, we need to establish a sufficient set of congruence criteria. The given information tells us that two sides and a non-included angle of ΔABC are congruent to the corresponding parts of ΔABD. However, this information alone is not enough to guarantee the congruence of the two triangles.
To establish congruence, we would need additional information, such as the congruence of another angle or side. Without that additional information, it is not possible to conclude that ΔEFG is congruent to ΔABD solely based on the given information.
Therefore, while there are some similarities between ΔEFG and ΔABD, such as the congruent sides and angle, we cannot definitively state that the two triangles are congruent without further information or congruence criteria being provided.
Learn more about triangles here:
https://brainly.com/question/2773823
#SPJ11
I need help anyone with graphs

Answers
The given function shows imply that the graph g(x) is shifted two units right and three units up.
Option B is correct.
What is the transformation of a function?The transformation of a function occurs in a fancy way such that a function maps itself. f: x → x.
From the given information:
Let's take a look at the function f(x) that goes through 0 just when x = 0. Now we want to move it to the right by 2. It implies that it has to go through 0 when x = +2.
Now, we have to add 2 to x, then the function becomes f'(x) = f(x-2) will be shifted by 2 units to the right.
Similarly, the same scenario occurs when shifting up. Again imagine your function passes 0 when x = 0. We have to add 3. Now, the function f’’(x) = f(x) + 3 will be shifted by 3 units up.
Combining the two transformations, we have:
g(x) = f(x-2) + 3Therefore, we can conclude that the function implies that the graph g(x) is shifted two units right and three units up.
Learn more about the transformation of functions here:
https://brainly.com/question/1548871
#SPJ1
Compute f′(a) algebraically for the given value of a. f(x)=−7x+5;a=−6
Answers
The f′(a) when a = −6 is -7. This means that the slope of the tangent line of the graph of f(x) at x = -6 is -7.
To compute f′(a) algebraically for the given value of a, we use the following differentiation rule which is known as the Power Rule.
This states that:If f(x) = xn, where n is any real number, then f′(x) = nxⁿ⁻¹This is valid for any value of x.
Therefore, we can differentiate f(x) = −7x + 5 with respect to x using the power rule as follows:
f(x) = −7x + 5
⇒ f′(x) = d/dx (−7x + 5)
⇒ f′(x) = d/dx (−7x) + d/dx(5)
⇒ f′(x) = −7(d/dx(x)) + 0
⇒ f′(x) = −7⋅1 = −7
Hence, the derivative of f(x) with respect to x is -7.Now, we evaluate f′(a) when a = −6 as follows:f′(x) = −7 evaluated at x = −6⇒ f′(−6) = −7
Therefore, f′(a) when a = −6 is -7. This means that the slope of the tangent line of the graph of f(x) at x = -6 is -7.
Learn more about Power Rule here:
https://brainly.com/question/23418174
#SPJ11
he lunch special at Saleh's Restaurant is a sandwich, a drink and a dessert. There are 2 sandwiches, 2 drinks, and 3 desserts to choose from. How many lunch specials are possible?
Answers
Answer:
2
Step-by-step explanation:
that's because there are two sandwiches and two drinks so one sandwich and drink is one lunch special
Ally rents a car for one day. It costs her $35 plus $0.35 per mile. Ally only has $134.75. How many miles can she drive?
Answers
Ally will be able to cover 285 miles for the trip
How to calculate the number of miles ?Ally wants to rent the car for one day
The rents costs $35 and $0.35 per mile
Ally has $134.75 to spend for the trip
The number of miles Ally can drive for the trip can be calculated as follows
134.75 - 35
= 99.75
99.75/0.35
= 285
Hence Ally will be able to drive 285 miles for the trip
Read more on miles here
https://brainly.com/question/7044088
#SPJ1
The tax rate at this restaurant is 9. 5%. Some other person’s sales tax is $1. 61. How much was their subtotal?
Answers
Answer:
1.76295
1.76( 1 dp)
Step-by-step explanation:
\($1. 61\)
\(1.61 \times 9.5 \\ 1.61 \times \frac{9.5}{100} \\ \frac{1.61}{1} \times \frac{9.5}{100} \\ \frac{ 15.295 }{100} \\ = 0.15295 \\ add \: 0.15295 \: to \: 1.61 \\ = 1.61 + 0.15295 \\ = 1.76295 \\ approx = 1.76\)
work out the equation of the line which has a gradient of 2
Answers
Answer:
y = 2x + 2
Step-by-step explanation:
Use decomposition to find the area of the figure.
3 cm top
5 cm middle
7 cm bottom
The area is ? square centimeters
Answers
The area of the figure is 23 square centimeters.
To find the area of the figure, we need to split it up into simpler shapes whose area we can easily calculate. The figure is a trapezoid, so we can split it up into a rectangle and two triangles.
The rectangle has a length of 5 cm and a width of 3 cm, so its area is:
A(rectangle) = length × width = 5 cm × 3 cm = 15 cm²
To find the area of each triangle, we first need to find the height of the trapezoid. The height is the perpendicular distance between the parallel sides, which is the distance between the bottom and top sides. The height of the trapezoid is:
height = 7 cm - 3 cm = 4 cm
Each triangle has a base of 2 cm (half of the top side of the trapezoid) and a height of 4 cm, so the area of each triangle is:
A(triangle) = (1/2) × base × height = (1/2) × 2 cm × 4 cm = 4 cm²
To find the total area, we add the areas of the rectangle and the two triangles:
A(total) = A(rectangle) + 2 × A(triangle)
= 15 cm² + 2 × 4 cm²
= 23 cm²
Therefore, the area of the figure is 23 square centimeters.
Learn more about :
Area of trapezoid : brainly.com/question/12221769
#SPJ11