An artist is designing a stained-glass window for a modern art museum. In her design ∠F is 110°, ∠AEF is y°, ∠BEC is 25° and ∠CED is 20°. She has five sections created and needs to determine the measure of the angle in the upper left corner to cut the last piece of glass to finish the piece, as shown in the figure below
Answers
To determine the measure of the angle in the upper left corner to cut the last piece of glass to finish the piece. Given that ,In the given figure, an artist is designing a stained-glass window for a modern art museum. In her design ∠F is 110°, ∠AEF is y°, ∠BEC is 25°, and ∠CED is 20°.
By angle sum property, we know that;∠AED + ∠CED + ∠F = 180°[∵ In ΔAED, ∠AED + ∠CED + ∠BEC = 180°]⟹ ∠AED = 180° - ∠CED - ∠F⟹ ∠AED = 180° - 20° - 110°⟹ ∠AED = 50°Now, we can calculate the value of y, in ΔAEF.As we know that, in ΔAEF,∠AEF + ∠AED + ∠F = 180°⟹ y + 50° + 110° = 180°⟹ y + 160° = 180°⟹ y = 20°Now, in ΔBEC, we can find the value of ∠BCE and in ΔDEF, we can find the value of ∠EFD.∠BCE = 180° - ∠BEC - ∠CED⟹ ∠BCE = 180° - 25° - 20°⟹ ∠BCE = 135°∠EFD = ∠BCE⟹ ∠EFD = 135°In ΔDEF,∠EFD + ∠F = 180°⟹ 135° + ∠F = 180°⟹ ∠F = 180° - 135°⟹ ∠F = 45°Now, we can find the value of ∠ABD,∠ABD = ∠AEF + ∠F⟹ ∠ABD = 20° + 45°⟹ ∠ABD = 65°Therefore, the measure of the angle in the upper left corner to cut the last piece of glass to finish the piece is 65°.
Learn more about angle here:
https://brainly.com/question/31818999
#SPJ11
Related Questions
Can you help me, please?

Answers
can someone help pls

Answers
The radius of the ball, to the nearest hundredth, is approximately 10.63 cm.
To find the radius of the spherical ball, we'll use the formula for the surface area of a sphere, which is given by:
Surface Area = 4πr²
Given that the surface area of the ball is 452 cm², we can set up the equation:
452 = 4πr²
Dividing both sides of the equation by 4π, we get:
113 = r²
Taking the square root of both sides, we find:
r ≈ √113
Evaluating √113 to the nearest hundredth, we have:
r ≈ 10.63 cm
Therefore, the radius of the ball, to the nearest hundredth, is approximately 10.63 cm.
To learn more about the surface area of the sphere;
https://brainly.com/question/14692728
#SPJ1
what is slope. and what is it do
Answers
Answer:
Step-by-step explanation:
Slope is the steepness of a line as it moves from LEFT to RIGHT. Slope is the ratio of the rise, the vertical change, to the run, the horizontal change of a line. The slope of a line is always constant (it never changes) no matter what 2 points on the line you choose.
HELP PLEASE 2x+2<-4x+22<6x+10
Answers
Answer:
6//5,10/3
Step-by-step explanation:
maybe hope this is help
Please answer my question now in two minutes

Answers
Answer:
given,triangle EFG is congruent to triangle HIJ,THEIR corresponding sides are equal,
so, 10x=x+45
10x_x=45
or,9x=45
therefore , x=5
again,
3y = y+14
or, 3y_y=14
or, y=14/2
therefore the value of y is 7.
so the value of x is 5 and y is 7.
hope its helpful to uh...
Peter compra 8 limones por $6. Cada limón tiene el mismo precio.
¿Cuál es el costo de 1 limón?
Answers
Respuesta:
Cada limón cuesta $0.75
Explicación:
$6 ➗ 8 limones = $0.75 por limon
Espero que esto ayude. Lo siento si está mal. Eres amado y eres hermoso/guapo
-Bee
Math school please need help

Answers
Answer:
r² = (9 - 4)² + (6 - 4)² = 5² + 2² = 25 + 4 = 29
So the equation of this circle is
(x - 4)² + (y - 4)² = 29
Six less then a number is equal to ten
Answers
n-6=10
To solve, add 6 to each side, giving you n=16
According to the information we can infer that the number is 16. So, 6 - 16 is 10.
What number does complete the operation correctly?Let's assume the number is represented by 'x'.
According to the given information, six less than a number is equal to ten. This can be expressed as:
x - 6 = 10To find the value of 'x', we can add 6 to both sides of the equation:
x - 6 + 6 = 10 + 6This simplifies to:
x = 16According to the information we can conclude that the number is 16. So, 6 - 16 is 10.
Learn more about numbers in: https://brainly.com/question/24908711
#SPJ2
30.016
Give your answer to two decimal places.
Answers
Answer:
3001.6
Step-by-step explanation:
Move the decimal twice to the right
Right triangle FGH is shown. Which pair of expressions is equal to 9/41?
A. Sin F and Cos G
B. Sin F and Tan G
C. Tan Fand Sin G
D. Cos F and Sin G

Answers
Answer
A
Step-by-step explanation:
1,400 people traveled through a specific train station yesterday.Today, the number of people traveling through increased by 40%. how many peopled traveled through the train station today? please help
Answers
Answer: 1960
Step-by-step explanation:
Simple percentage. We have 1,400 as a base. To increase by a fraction divide the fraction by 100, add 1 and then multiply by the base. We have 40, and 40/100 = 0.4. We add one to get 1.4 and multiply 1,400 by it to get 1960
Write an iterated integral for a. vertical cross-sections, b. horizontal cross-sections. S Sa dA over the region R bounded by y=ex, y = 1, and x = - R In 5.
Answers
The iterated integral for vertical cross-sections is:
∫ from -R ln(5) to 0 ∫ from ex to 1 f(x, y) dy dx
The iterated integral for horizontal cross-sections is:
∫ from -∞ to -R ln(5) ∫ from ex to 1 f(x, y) dx dy
a. For vertical cross-sections:
To set up an iterated integral for vertical cross-sections, we integrate with respect to x first and then integrate with respect to y.
The region R is bounded by y = ex,
y = 1, and
x = -R ln(5).
The limits of integration for x are from x = -R ln(5) to
x = 0, and the limits of integration for y are from
y = ex to
y = 1.
Therefore, the iterated integral for vertical cross-sections is:
∫∫R f(x, y) dy dx
= ∫ from -R ln(5) to 0 ∫ from ex to 1 f(x, y) dy dx
b. For horizontal cross-sections:
To set up an iterated integral for horizontal cross-sections, we integrate with respect to y first and then integrate with respect to x.
The region R is bounded by y = ex,
y = 1, and
x = -R ln(5).
The limits of integration for y are from y = ex to
y = 1, and the limits of integration for x are from
x = -∞ to
x = -R ln(5).
Therefore, the iterated integral for horizontal cross-sections is:
∫∫R f(x, y) dx dy
= ∫ from -∞ to -R ln(5) ∫ from ex to 1 f(x, y) dx dy
In both cases, the specific function f(x, y) that needs to be integrated depends on the problem context or the given information.
To know more about integral visit
https://brainly.com/question/31433890
#SPJ11
find the general solutions to the following inhomogeneous first-order linear differential equations using the particular solution method: i. y 0 3y
Answers
The general solution to the given differential equation is y(t) = C * e^(3t).
To find the general solution to the inhomogeneous first-order linear differential equation y'(t) - 3y(t) = 0, follow these steps:
Step 1: Identify the homogeneous equation, which is y'(t) - 3y(t) = 0.
Step 2: Solve the homogeneous equation by finding the general solution. In this case, it is y_h(t) = C * e^(3t), where C is a constant.
Step 3: Identify the inhomogeneous part of the equation, which is missing in this case. Since the given equation is already homogeneous, there is no need to find a particular solution.
Step 4: Combine the homogeneous solution and the particular solution (if present) to form the general solution. In this case, the general solution is y(t) = y_h(t) = C * e^(3t).
So, the general solution to the given differential equation is y(t) = C * e^(3t).
Learn more about Equation
brainly.com/question/24169758
#SPJ11
The function f(x)=200/x + 10 models the cost per student of a field trip when x students go on the trip. How is the parent function f(x)=1/x transformed to create the function f(x)=200/x + 10
Answers
Answer:
Step-by-step explanation:
We need to explain the transformations applied to 1/x to get f(x). We get f by following the following steps.
1. Multiply 1/x by 200 to get the function 200/x. This represents taking the graph of 1/x and expanding it vertically by a factor of 200.
2. Sum 10 units to 200/x. This represents a vertical shift of 10 units to the graph of 200/x.
what is the probability that if 8 letters are typed, no letters are repeated? the probability that no letters are repeated is
Answers
The probability that no letters are repeated is 0.4121.
Divide the total number of outcomes by the entire number of different ways an event could happen to arrive at the probability. There are differences between probability and odds. The possibility of an event happening divided by the likelihood that it won't happen yields the odds. Probability is a metric used to assess the likelihood that a specific event will occur. The likelihood that the coin will land with the heads side up is measured using the probability concept when we toss it in the air. Here is an example of how probability is used in everyday life that you probably already know about. Prior to a major outing, we always consult the weather prediction.
So, the probability
Given, Number of letters=8
N\(=26*25*24*23*22*21*20*19\)
P\(=\frac{25}{26}*\frac{24}{26}*\frac{23}{26}*\frac{22}{26}*\frac{21}{26}*\frac{20}{26}\\=0.96*0.92*0.88*0.85*0.81*0.77\\=0.4121\)
Learn more about probability here
https://brainly.com/question/13604758
#SPJ4
Barbie has a favorite number. The
quotient of her number and -4 is -90.
What is Barbie's favorite number?
Answers
Answer:
Is -4444444444
Step-by-step explanation:
Answer:
360
Step-by-step explanation:
A quotient is the result of a division problem.
We must multiply -4 and -90.
-4 • -90 = 360
(There is no - because a negative multiplied by a negative equals a positive.)
plzzzzzzzz help this is math

Answers
m= -25
Answer:
5
Step-by-step explanation:
Simplify the equation:
2m -10 = -3m +15
Add 3m
5m -10 = 15
Add 10
5m = 25
Divide by 5
m = 5
did we prove the conclusion true for every isosceles triangle or only for this specific isosceles triangle?
Answers
∠A = ∠C for every isosceles triangle and not only for this specific isosceles triangle.
We are given that:
AB = BC
Now, draw a angle bisector from point B to the line AC in a way that it intersects AC at D.
Now, we get that:
∠ABD = ∠CBD ( BD is the angle bisector)
BD = BD ( common line)
So, ΔABD ≅ Δ CBD ( SAS property)
So,
∠A = ∠ C ( CPCT rule)
Also, it will be true for every isosceles triangle.
Therefore, we get that, ∠A = ∠C for every isosceles triangle and not only for this specific isosceles triangle.
Learn more about triangles here:
https://brainly.com/question/17335144
#SPJ4
Your question was incomplete. Please refer the content below:
There is an isosceles triangle with AB = BC. Prove that ∠A = ∠C.
Did we prove the conclusion true for every isosceles triangle or only for this specific isosceles triangle.

Complete the equation so that it has no solution 9(x-4)-5x=
Answers
Answer:
9(x-4)-5x=
open brackets
9x-36-5x=0
relate with similar expressions
note,when negative crosses the equal sign,it becomes positive
9x-5x=36
4x=36
x=9
a+ 1 1/6 = 11 7/9
...........................
Answers
Answer:
a = 191/81
Step-by-step explanation:
a+ 1 1/6 = 11 7/9
1 1/6 = 7/6
11 7/9 = 106/9
So, our equation is
a + 7/6 = 106/9
Subtract 7/6 from both sides
a = 191/81
So, the answer is
a = 191/81
The time needed to complete a final examination in a particular college course is normally distributed with a mean of 80 minutes and a standard deviation of 10 minutes. Answer the following questions. Round the intermediate calculations for z value to 2 decimal places. Use Table 1 in Appendix B. a. What is the probability of completing the exam in one hour or less (to 4 decimals)? b. What is the probability that a student will complete the exam in more than 60 minutes but less than 75 minutes (to 4 decimals)? c. Assume that the class has 60 students and that the examination period is 90 minutes in length. How many students do you expect will be unable to complete the exam in the allotted time (to the next whole number)?
Answers
a) The probability of completing the exam in one hour or less is 0.0228
b) The probability that a student will complete the exam in more than 60 minutes but less than 75 minutes is 0.2857
c) students that will be unable to complete the exam in the allotted time are 10 students
What is probability?
Simply put, probability measures how probable something is to occur. We can discuss the probabilities of various outcomes, or how likely they are, whenever we are unsure of how an event will turn out. Statistics is the study of events subject to probability.
Given data:
mean = \(\mu\) = 80
standard deviation = \(\sigma\) = 10
a) The probability of completing the exam in one hour or less:
P(x \(\leq\) 60) ( 1 hour = 60 minutes)
= P[(x - \(\mu\)) /\(\sigma \leq\) (60 - 80) / 10]
= P(z \(\leq\) -2.00)
from z table,
= 0.0228
b) The probability that a student will complete the exam in more than 60 minutes but less than 75 minutes:
P(60 < x < 75) = P[(60 - 80)/ 10 ) < (x - \(\mu\)) /\(\sigma\) < (75 - 80) / 10 ) ]
= P(-2.00 < z < -0.50)
= P(z < -0.50) - P(z < -2.00)
from z table,
= 0.3085 - 0.0228
= 0.2857
c) students that will be unable to complete the exam in the allotted time :
n = 60
P(x > 90) = 1 - p( x< 90)
=1- p P[(x - \(\mu\)) /\(\sigma\) < (90 - 80) / 10]
=1- P(z < 1.00)
from z table,
= 1 - 0.8413
= 0.1587
= 60 * 0.1587 = 9.52
= 10 students
To learn more about the probability from the given link
https://brainly.com/question/24756209
#SPJ1
Solve for b in the literal equation y = 10x + 10b
Answers
Answer:
x+y/10-b
Step-by-step explanation:
Factor out the common term: 10
Divide both sides by 10
Subtract b from both sides
Explain how to convert 44.0 gallons to liters.
Answers
It is instructed that we change 44.0 gallons to liters. One gallon is one unit of volume. A gallon is equivalent to 3.785 liters.
3.785411784 litres make to one US gallon. 4 quarts, 8 pints, or 128 fluid ounces make up a gallon. In American measurements, a gallon is equivalent to 3.785 litres, 128 fluid ounces, 4 quarts, 8 pints, or 16 cups. A gallon's volume is about equivalent to 3.78541 litres. Thus, a gallon is more than three litres. A gallon of one liquid could weigh differently than a gallon of another. As one imperial gallon is equal to 4.54609 litres, it takes up space that is nearly 4,546 cubic centimetres (roughly a 16.5cm cube). An average glass holds eight ounces. So, 16 eight-ounce glasses of water make up a gallon.
44.0 gallons to 3.785 liters.
Learn more about gallon here
https://brainly.com/question/28274339
#SPJ4
(c) A non-uniform but spherically symmetric charge distribution has a charge density: rho(r)=rho 0
(1−r/R)
rho(r)=0
for r≤R
for r>R
where rho 0
=3Q/πR 3
is a positive constant. Show that the total charge contained in this charge distribution is Q. [4] Show that the electric field in the region r>R is identical to that created by a point charge Q at r=0 [2] Derive an expression for the electric field in the region r≤R. [5]
Answers
To show that the total charge contained in the charge distribution is Q, we integrate the charge density over the entire volume. The charge density is given by:
ρ(r) = ρ₀(1 - r/R) for r ≤ R,
ρ(r) = 0 for r > R,
where ρ₀ = 3Q/πR³.
To find the total charge, we integrate ρ(r) over the volume:
Q = ∫ρ(r) dV,
where dV represents the volume element.
Since the charge density is spherically symmetric, we can express dV as dV = 4πr² dr, where r is the radial distance.
The integral becomes:
Q = ∫₀ᴿ ρ₀(1 - r/R) * 4πr² dr.
Evaluating this integral gives:
Q = ρ₀ * 4π * [r³/3 - r⁴/(4R)] from 0 to R.
Simplifying further, we get:
Q = ρ₀ * 4π * [(R³/3) - (R⁴/4R)].
Simplifying the expression inside the parentheses:
Q = ρ₀ * 4π * [(4R³/12) - (R³/4)].
Simplifying once more:
Q = ρ₀ * π * (R³ - R³/3),
Q = ρ₀ * π * (2R³/3),
Q = (3Q/πR³) * π * (2R³/3),
Q = 2Q.
Therefore, the total charge contained in the charge distribution is Q.
To show that the electric field in the region r > R is identical to that created by a point charge Q at r = 0, we can use Gauss's law. Since the charge distribution is spherically symmetric, the electric field outside the distribution can be obtained by considering a Gaussian surface of radius r > R.
By Gauss's law, the electric field through a closed surface is given by:
∮E · dA = (1/ε₀) * Qenc,
where ε₀ is the permittivity of free space, Qenc is the enclosed charge, and the integral is taken over the closed surface.
Since the charge distribution is spherically symmetric, the enclosed charge within the Gaussian surface of radius r is Qenc = Q.
For the Gaussian surface outside the distribution, the electric field is radially directed, and its magnitude is constant on the surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q,
Simplifying:
E = Q / (4πε₀r²).
This is the same expression as the electric field created by a point charge Q at the origin (r = 0).
To derive an expression for the electric field in the region r ≤ R, we can again use Gauss's law. This time we consider a Gaussian surface inside the charge distribution, such that the entire charge Q is enclosed.
The enclosed charge within the Gaussian surface of radius r ≤ R is Qenc = Q.
By Gauss's law, we have:
∮E · dA = (1/ε₀) * Qenc.
Since the charge distribution is spherically symmetric, the electric field is radially directed, and its magnitude is constant on the Gaussian surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q.
Simplifying:
E = Q / (4πε₀r²).
This expression represents the electric field inside the charge distribution for r ≤ R.
Learn more about charge here:
https://brainly.com/question/18102056
#SPJ11
How to solve 400 divided by 1,600
Answers
Answer:
1/4
Step-by-step explanation:
400 divided by 1600 = \(\frac{400}{1600}\)
We simplify by 400, and get the answer
1/4
Answer:
0.25 or 1/4
Step-by-step explanation:
1600/400
1600 cant go into 400 so you start with zero, add a decimal next to your zero, and carry down a 1. That then becomes 1600/4000 divide that and drop the decimal to equal 0.25.
If you invest $10000 compounded continuously at 6% p.a. how much will this investment be worth in 6 years?
Answers
Your investment of $10000 compounded continuously at 6% p.a. would be worth $14,366.00 after 6 years.
If you invest $10000 compounded continuously at 6% p.a., the formula for calculating the value of your investment after 6 years would be:
A = Pe^(rt)
Where A is the final amount, P is the principal investment amount, e is Euler's number (approximately 2.718), r is the interest rate (in decimal form), and t is the time period (in years).
Plugging in the given values, we get:
A = 10000e^(0.06*6)
A = 10000e^(0.36)
A = 10000*1.4366
A = $14,366.00
Therefore, your investment of $10000 compounded continuously at 6% p.a. would be worth $14,366.00 after 6 years.
Learn more about compounded continuously here:
brainly.com/question/14652283
#SPJ11
If x+4/4 = y+7/7 then x/4 =___.
(Number 9 is the one I need an answer for)
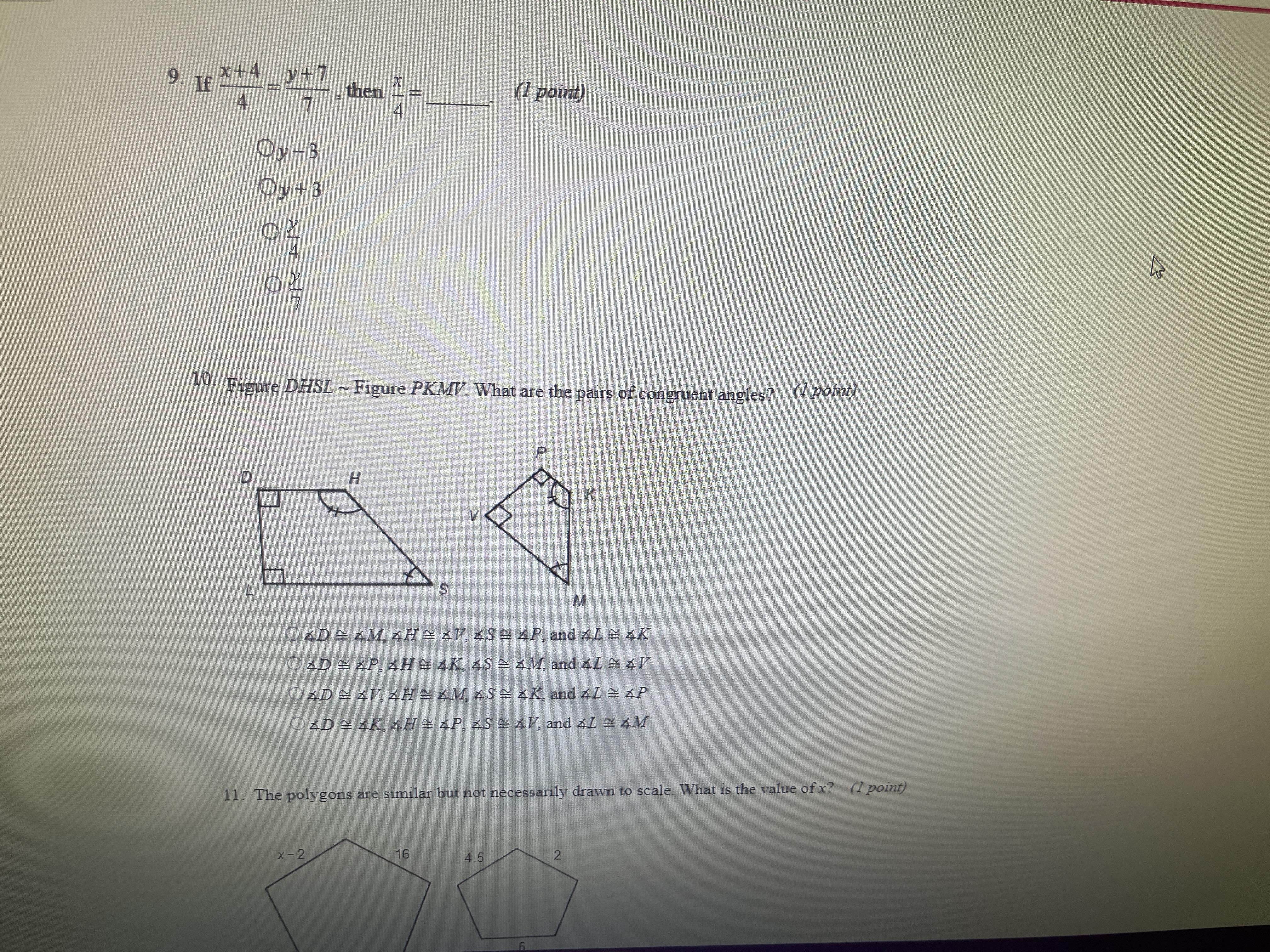
Answers
Answer:
4th answer is correct
Step-by-step explanation:
First, let us make x the subject.
\(\sf \frac{x+4}{4} =\frac{y+7}{7}\)
Use cross multiplication.
\(\sf 7(x+4)=4(y+7)\)
Solve the brackets.
\(\sf 7x+28=4y+28\)
Subtract 28 from both sides.
\(\sf 7x=4y+28-28\\\\\sf7x=4y\)
Divide both sides by 7.
\(\sf x=\frac{4y}{7}\)
Now let us find the value of x/4.
To find that, replace x with (4y/7).
Let us find it now.
\(\sf \frac{x}{4} =\frac{\frac{4y}{7} }{4} \\\\\sf \frac{x}{4} =\frac{4y}{7}*\frac{1}{4} \\\\\sf \frac{x}{4} =\frac{4y}{28}\\\\\sf \frac{x}{4} =\frac{y}{7}\)
In a sequence of numbers, the first term is x and each term thereafter is twice the previous term. the fifth term is 160. what is the value of x ?
Answers
The value of x in sequence of number is 10.
Here, first term of sequence is x and each term there after is twice the previous term. Also Fifth term is 160.
What is geometric series?
Geometric series is an infinite series of the form:
\(a+ar+a r^{2} +ar^{3} +..........\)
where r is known as common ratio.
Now, first term is x and each term there after is twice the previous term.
So the series will be;
x , 2x , 4x , 8x, ..........
Clearly this series is geometric series with common ratio 2.
And the nth term of geometric series is \(ar^{n-1}\)
⇒ fifth term is 160
\(ar^{5-1} = 160\\ar^{4} = 160\\a 2^{4} =160\\a=\frac{160}{16} \\a=10\)
Here, first term is x.
The value of x in sequence of number is 10.
Learn more about the geometric series visit:
https://brainly.com/question/24643676
#SPJ1
Darlene has 634 gallons of gasoline. Every time she mows her lawn, she uses 38 gallon. How many times can she mow her lawn before she needs more gas?
Answers
Answer: 16 times
Step-by-step explanation:
So in this situation, an equation helps!
634 = 38x
Where 634 is the number of gallons of gas she has; 38x is how much she needs to mow her lawn each time.
Now simply divide!
If we round we get x= 16.68 however this is not the correct answer because you can't mow 68/100 of a lawn! So even though 0.68 is greater than 0.5, we would round down to 16.
Could the number of cars owned be related to whether an individual has children? In a local town, a simple random sample of 200 residents was selected. Data was collected on each individual on how many cars they own and whether they have children. The data was then presented in the frequency table:
Number of Vehicles Do you have children Total
No Yes
Zero: 24 50 74
One: 27 25 52
Two or more: 57 17 74
Total: 108 92 200
Part A: What proportion of residents in the study have children and own at least one car? Also, what proportion of residents in the study do not have children and own at least one car? (2 points)
Part B: Explain the association between the number of cars and whether they have children for the 200 residents. Use the data presented in the table and proportion calculations to justify your answer. (4 points)
Part C: Perform a chi-square test for the hypotheses.
H0: The number of cars owned by residents of a local town and whether they have children have no association.
Ha: The number of cars owned by residents of a local town and whether they have children have an association.
What can you conclude based on the p-value?
Answers
The probability of number of 1-2 Children in car and 3 plus children in car is 0.203.
We have,
The possibility of the result of any random event is known as probability. This phrase refers to determining the likelihood that any given occurrence will occur.
The probability of P(1-2 children| car). P (3 plus children| car) is given by:
P = 63/88 × 25/88
P=0.203
The probability of P(Bus| 1-2 children). P (Bus | 3 plus children) is given by:
P = 38/101 × 49/74
P=0.249
The probability of P(Car |1-2 Children) is given by:
P= 63/101
P=0.624
The probability of P(3 plus children | Bus)is given by:
P=49/87
P=0.563
Learn more about probability here:
brainly.com/question/30034780
#SPJ1
complete question:
Drag the tiles to the boxes to form correct pairs. Not all tiles will be used.
The table shows the mode of transportation to school for families with a specific number of children.
Mode of Transportation
Car
Number of
Children
0.284
1-2
63
38
3+
25
49
Total
88
87
A family from the survey is selected at random. Match the probability to each event.
0.662
Bus
0.203
0.249
101
74
175
0.624
P (3+ Children Bus)
Total
P(1-2 Children Car) - P (3+ Children Car)
Reset
P (Car 1-2 Children)
0.563
P (Bus 1-2 Children) - P (Bus 3+ Children)
▸