An artist is working on the design of a logo for the T-shirts that the participants
in the walk will receive. He starts by drawing LADC so that it measures 60'
Next, he draws segment DB so that m BDC is 10° greater than mŁADB.

Answers
Answer:
m(∠ADB) = 25 degrees
m(∠BDC) = 35 degrees
Step-by-step explanation:
Measure of angle ADC of the logo = 60°
Measure of angle ADB = x°
And measure of angle BDC = (x + 10)°
Since, angle ADC is a combination of two angles,
Therefore, measure of angle ADC = m(∠ADB) + m(∠CDB)
x° + (x + 10)° = 60°
2x + 10 = 60
2x = 50
x = 25
Measure of angle ADB = x = 25 degrees
Measure of angle BDC = (x + 10)°
= (25 + 10)°
= 35 degrees
Related Questions
Pls answer and show me how you got that answer

Answers
The mass of the radioactive sample at the beginning of the 13th day of the experiment will be around 424.7 grams.
What does one gramme represent?A metric weight measurement unit. A gramme is one thousandth of a kilogramme, or about 30 times smaller than an ounce. Leave a space between the word "gramme" (or the symbol "g") and the number that comes before it when a specific number is provided. In technical and scientific writing, the unit name and the number are either written together in full (for example, ten grammes) or a numeral is used with the sign ( e.g. 10 g ).
When we find the mass of radioactive, we obtain:
m₀=initial mass=1500 grams, r = 13% and n =12 days
⇒m = m₀ x \((1 - \frac{r}{100} )^{n}\)
⇒m =1500×\((1-\frac{13}{100}) ^{12}\)
⇒m=424.7 grams.
To know more about grams visit:
https://brainly.com/question/29127168
#SPJ1
Select the correct answer.
What is the approximate value of the correlation coefficient for the given graph

Answers
Answer:
x = -5
Step-by-step explanation:
the answer is -5 sussy baka
This is because all points are on, or nearly on, the same straight line that has a negative slope. We consider this close to or nearly perfect negative linear correlation.
Side note: The r value and slope are both negative, but they aren't equal to one another.
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
Find three consecutive even integers such that the
sum of the smallest and the largest is 36.
Answers
n= smallest integer
n+2= middle integer
n+4= largest integer
n + n + 4 = 36
2n+ 4 = 36
2n=32
n= 16 which means that the smallest integer is 16
then you substitute it into the equation for the largest integer
n+4=20
16, 18, 20 is the answer
Which system of inequalities does the graph represent?
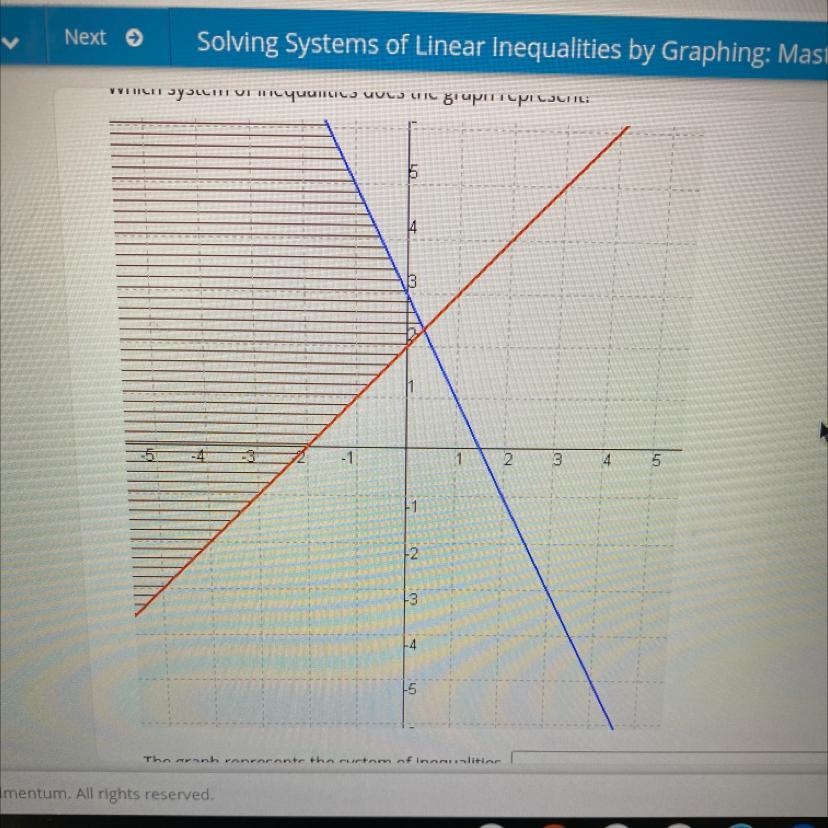
Answers
Answer:system of linear equalities in one variable .
Step-by-step explanation:
What is the profit function P(x)

Answers
The profit function for this problem is given as follows:
P(x) = -0.5x³ + 100x² - 500x + 300.
How to obtain the profit function?The profit function is obtained as the subtraction of the revenue function by the cost function, as follows:
P(x) = R(x) - C(x).
The functions for this problem are given as follows:
R(x) = -0.5x³ + 600x² - 200x + 300.C(x) = 500x² + 300x.Hence the profit function is given as follows:
P(x) = -0.5x³ + 600x² - 200x + 300 - 500x² - 300x
P(x) = -0.5x³ + 100x² - 500x + 300.
More can be learned about profit function at brainly.com/question/16866047
#SPJ1
3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
There are 4 pink, 5 yellow, 2 violet and 3 gray marbles
in a hat. You pick 2 marbles from the hat. Marbles are
NOT returned to the hat.
P(pink, then violet)
P(gray, then gray)
P(not yellow, not yellow)
P(yellow, not yellow)
Answers
================================================
Work Shown for problem 1
P(pink, then violet) = P(pink)*P(violet given 1st was pink)
= (4/14)*(2/13)
= 8/182
= 4/91
------------------------------
Work Shown for problem 2
P(gray, then gray)
= P(gray)*P(gray given 1st was gray)
= (3/14)*(2/13)
= 6/182
= 3/91
-------------------------------
Work Shown for problem 3
P(not yellow, not yellow)
= P(not yellow)*P(not yellow given 1st was not yellow)
= (9/14)*(8/13)
= 72/182
= 36/91
-------------------------------
Work Shown for problem 4
P(yellow, not yellow)
= P(yellow)*P(not yellow given 1st was yellow)
= (5/14)*(9/13)
= 45/182
(a) The perimeter of a rectangular garden is 320 m.
If the width of the garden is 74 m, what is its length?
(b) The area of a rectangular window is 5723 cm?
If the length of the window is 97 cm, what is its width?
Width of the window: cm what is the width
Answers
Answer:
86 m, 59 cm
Step-by-step explanation:
a. perimeter is 2L + 2W
320 = 2L + 2(74)
320 = 2L + 148
172 = 2L
86 m is length
b. area = L x w
5723 = 97 x w
5723/97 = 2
59 cm is width
Whirly Corporation’s contribution format income statement for the most recent month is shown below:
Total Per Unit
Sales (8,700 units) $ 287,100 $ 33.00
Variable expenses 165,300 19.00
Contribution margin 121,800 $ 14.00
Fixed expenses 55,600
Net operating income $ 66,200
Required:
(Consider each case independently):
1. What would be the revised net operating income per month if the sales volume increases by 40 units?
2. What would be the revised net operating income per month if the sales volume decreases by 40 units?
3. What would be the revised net operating income per month if the sales volume is 7,700 units?
Last month when Holiday Creations, Incorporated, sold 37,000 units, total sales were $148,000, total variable expenses were $115,440, and fixed expenses were $35,800.
Required:
1. What is the company’s contribution margin (CM) ratio?
2. What is the estimated change in the company’s net operating income if it can increase sales volume by 500 units and total sales by $2,000? (Do not round intermediate calculations.)
Answers
1. Revised Net Operating Income = $66,760
2. Revised Net Operating Income =$64,640
3. Revised Net Operating Income =$52,
1. If the sales volume increases by 40 units:
So, New Sales = 8,700 units + 40 units = 8,740 units
and, New Contribution Margin =
= $14.00 x 8,740 units
= 122, 360
New Fixed Expenses remain the same at $55,600
Then, Revised Net Operating Income
= New Contribution Margin - New Fixed Expenses
= 122360 - 55600
= 66,760.
2. If the sales volume decreases by 40 units:
New Sales = 8,700 units - 40 units = 8,660 units
New Contribution Margin
= 14 x 8660
= 121,240
New Fixed Expenses remain the same at $55,600
Then, Revised Net Operating Income
= New Contribution Margin - New Fixed Expenses
= 65,640
3. If the sales volume is 7,700 units:
New Sales = 7,700 units
New Contribution Margin
= 14 x 7700
= 107,800
New Fixed Expenses remain the same at $55,600
Then, Revised Net Operating Income
= New Contribution Margin - New Fixed Expenses
= 52, 200
Learn more about Income Format here:
https://brainly.com/question/15312142
#SPJ1
Factorise fully
40-10g
Please do quick, will mark brainiest!!
Answers
Answer:
10(4-g)Step-by-step explanation:
\(40 - 10g\)
Rewrite 40 as 4 × 10
\(4 \times 10 - 10g\)
Factor out 10
\(10(4 - g)\)
Make a frequency table using five classes.
class 31-38 39-46 47-54 55-62 63-70
f
11
24
15
7
3
Then estimate the mean and sample standard deviation using the frequency table. (Round s to two decimal places.)

Answers
Answer: C
Step-by-step explanation:
Jug A contains 6/7 as much water as Jug B.Jug C contains 3/5 as much water as Jug A.Find the ratio of the volume of water in Jug B to the volume of water as Jug C.
Answers
The ratio of the volume of water in Jug B to the volume of water in Jug C is 35:18.
Let's assume the volume of water in Jug B is x.
According to the given information, Jug A contains 6/7 as much water as Jug B. Therefore, the volume of water in Jug A can be calculated as (6/7) * x.
Similarly, Jug C contains 3/5 as much water as Jug A. Hence, the volume of water in Jug C can be expressed as (3/5) * [(6/7) * x].
To find the ratio of the volume of water in Jug B to the volume of water in Jug C, we divide the volume of water in Jug B by the volume of water in Jug C:
(x) / [(3/5) * (6/7) * x]
Simplifying the expression, we get:
x / (18/35 * x)
The x values cancel out, leaving us with:
1 / (18/35)
To simplify further, we multiply the numerator and denominator by the reciprocal of the denominator:
1 * (35/18)
The final ratio is:
35/18
For more such questions on ratio
https://brainly.com/question/30370621
#SPJ8
2x² + 5x, what will it a Perfect Square? make
Answers
Answer:
2x² + 5x + c = 0
For this quadratic equation to have one double root, the discriminant must equal 0.
5² - 4(2)(c) = 0
25 - 8c = 0
c = 25/8
2x² + 5x is not a perfect square because the coefficient of x², 2, is not a perfect square.
Explanation:2x² + 5x is not a perfect square.
A perfect square is an expression that can be factored into the square of a binomial. To determine if an expression is a perfect square, we can look at the coefficient of x². In this case, the coefficient is 2, which is not a perfect square.Learn more about Perfect Square here:https://brainly.com/question/34063927
#SPJ11
Match the prompts together.

Answers
When matched, the prompts on asymptotes would be:
Vertical asymptote at x=0: The cost of producing pills can never reach 0.Decreasing on (0,∞): As the number of pills produced gets smaller, the average cost of production greatly increases.Horizontal asymptote at y=0: The cost of producing pills cannot be negative.Positive on (0,∞): As more pills are produced, the average cost per pill decreases.How to match the asymptote statements ?The presence of a vertical asymptote at x=0 signifies that the cost of producing pills can never reach a value of 0, remaining persistently positive. Simultaneously, the horizontal asymptote at y=0 serves as a reassuring indication that the cost of producing pills cannot be negative, as it steadfastly remains at or above zero.
This crucial constraint ensures that the cost incurred in the pill production process is always a non-negative quantity. Consequently, the prompt related to the impossibility of negative costs aligns with this notion.
Find out more on horizontal asymptote at https://brainly.com/question/1851758
#SPJ9
Find the exact value of sin G.A. √1010B. 3√1010C. 4√10D. 160

Answers
Given the Right Triangle EFG, you know that:
\(\begin{gathered} EF=4 \\ EG=12 \end{gathered}\)By definition:
\(sin\theta=\frac{opposite}{hypotenuse}\)Since, in this case:
\(\theta=G\)You can identify that:
\(\begin{gathered} opposite=EF=4 \\ hypotenuse=FG \end{gathered}\)In order to find the hypotenuse of the Right Triangle, you need to use the Pythagorean Theorem, which states that:
\(c=\sqrt{a^2+b^2}\)Where "c" is the hypotenuse, and "a" and "b" are the legs of the Right Triangle.
You can set up that:
\(\begin{gathered} c=FG \\ a=EG=12 \\ b=EF=4 \end{gathered}\)Therefore:
\(FG=\sqrt{12^2+4^2}=4\sqrt{10}\)Now you can determine that:
\(sinG=\frac{4}{4\sqrt{10}}\)Simplify:
\(sinG=\frac{1}{\sqrt{10}}\)You can multiply the numerator and the denominator by:
\(\sqrt{10}\)In order to Rationalize the denominator:
\(sinG=\frac{1\cdot\sqrt{10}}{\sqrt{10}\cdot\sqrt{10}}\)\(sinG=\frac{1\cdot\sqrt{10}}{(\sqrt{10})^2}\)\(sinG=\frac{\sqrt{10}}{10}\)Hence, the answer is: Option A.
90 dollars ratio in 1:2:3
Answers
Answer:
3:6:9
Step-by-step explanation:
1/1+2+3 × 90 = 15
2/1+2+3 × 90 = 30
3/1+2+3 × 90 = 45
The radius of a circle is 3 m. Find its area in terms of pi.
Answers
Answer:
A = 9π m²
Step-by-step explanation:
the area (A) of a circle is calculated as
A = πr² ( r is the radius )
= π × 3²
= 9π m²
the price of a garment is reduced by 15% in sale to $30. find its original price
Answers
Answer:
x =35.29
Step-by-step explanation:
If it is reduced by 15%, you are paying 100-15 = 85%
The original price is x
x* 85% = 30
x *.85 = 30
Divide each side by x
x = 30/.85
x =35.29
Answer:
$25.50
Step-by-step explanation:
if 85% of $30 is $4.50, we subtract $4.50 from $30 and get $25.50
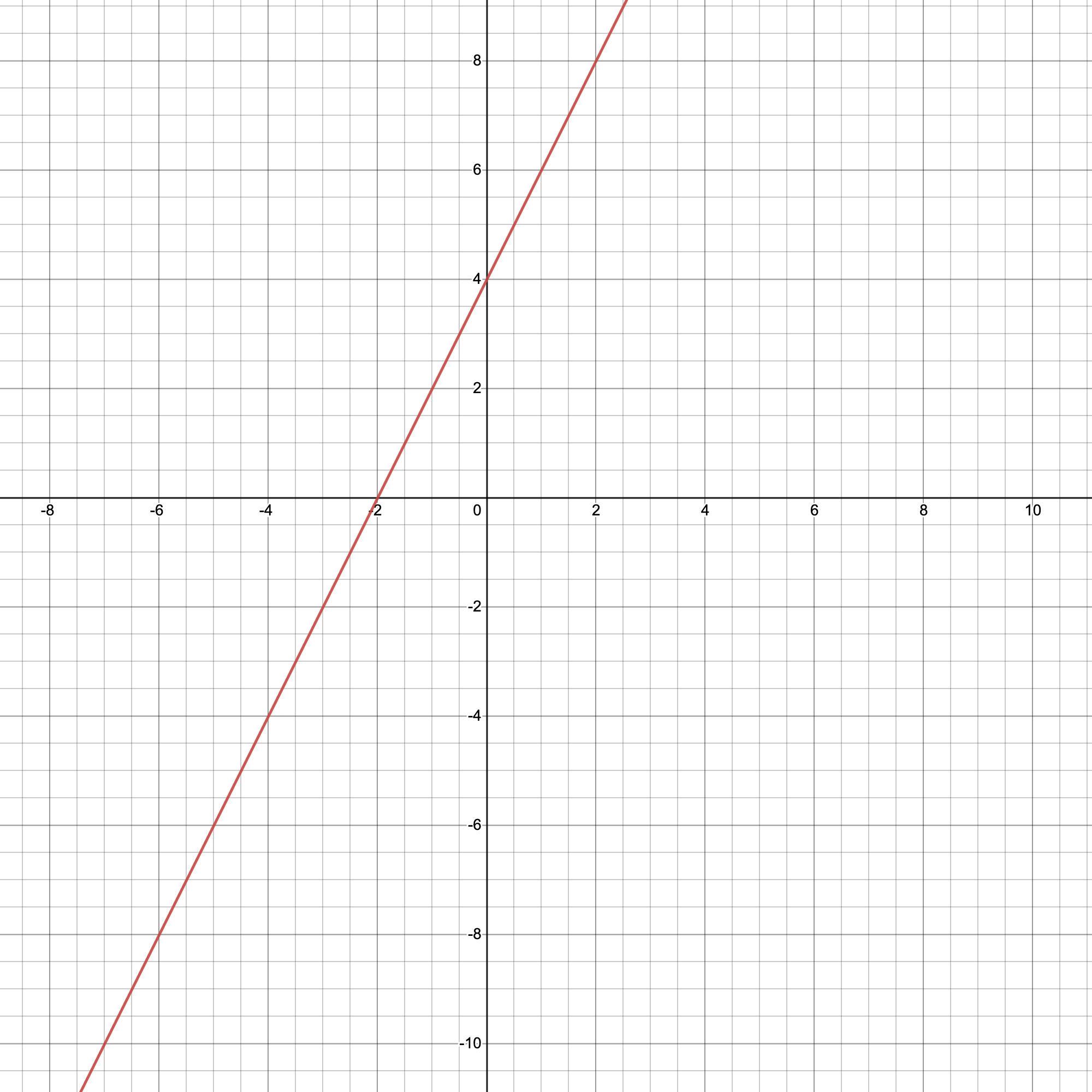
Graph each equation using the intercepts. Re-write in standard form first if necessary 2x-y=-42x=-4X=-2(2,0)O-y- -4Y=4(0,4)

Answers
EXPLANATION:
Given;
We are given the linear equation below;
\(2x-y=-4\)Required;
We are required to graph the equation of the line using the intercepts.
Step-by-step solution;
The graph of a line in standard form is given as;
\(Ax+By=C\)Note that the equation given already satisfies this condition. We can re-arrange the equation in the slope-intercept form which is;
\(y=mx+b\)We now have the following;
\(\begin{gathered} 2x-y=-4 \\ Subtract\text{ }2x\text{ }from\text{ }both\text{ }sides: \\ -y=-4-2x \\ Multiply\text{ }all\text{ }through\text{ }by\text{ }-1: \\ \\ y=4+2x \\ OR \\ y=2x+4 \end{gathered}\)We can plot for at least 2 points by using the intercepts, that is when x = 0 and when y = 0;
\(\begin{gathered} When\text{ }x=0: \\ y=2(0)+4 \\ \\ y=4 \end{gathered}\)Also,
\(\begin{gathered} When\text{ }y=0: \\ 0=2x+4 \\ Subtract\text{ }2x\text{ }from\text{ }both\text{ }sides: \\ -2x=4 \\ Divide\text{ }both\text{ }sides\text{ }by\text{ }-2: \\ x=-2 \end{gathered}\)We now have the points;
\((0,4)\text{ }and\text{ }(-2,0)\)We can now plot these on a graph paper, and then extend the line at both ends. That is at the point where you have (-2, 0), we can draw the line continuously to the left and from the point where you have (0, 4), you can also draw the line continuously to the right.
With the aid of a graphing tool, the graph will come out like the one shown below;
ANSWER:
Suppose that the weight (in pounds) of an airplane is a linear function of the amount of fuel (in gallons) in its tank. When carrying 15 gallons of fuel, the airplane weighs 1984 pounds. When carrying 40 gallons of fuel, it weighs 2124 pounds. How much does the airplane weigh if it is carrying 50 gallons of fuel?
Answers
8 cents is what fraction of a quarter?
Answers
Answer:
8/25
Step-by-step explanation:
Answer:
It is 8/25. hope this helps you
The equation that represents ⨀A is (x+1)2+(y−1)2=16. Determine whether point B(3,1) is on the circle.
Answers
Answer:
Step-by-step explanation:
center=(-1,1)
radius=√16=4
distance between (-1,1) and (3,1)=√[(3+1)²+(1-1)²]=√[16+0]=√16=4=radius
Hence point lies on the circle.
Kelly rolled scores of 254, 202, 284, 269, 151, 258 and 202 in a recent tournament. What was the mean, median and mode of her scores?
Answers
Answer:
See below!
Step-by-step explanation:
Data:254, 202, 284, 269, 151, 258, 202
Mean:The sum of data divided by the number of data is called mean.Mean of the data:
\(\displaystyle Mean= \frac{Sum \ of \ data}{number \ of \ data} \\\\Mean = \frac{254+202+284+269+151+258+202}{7} \\\\Mean=\frac{1620}{7} \\\\\boxed{Mean = 231.4}\)
Median:The middle value of the data is median.Median of data:
Arrange the data in increasing order.
151, 202, 202, 254, 258, 269, 284
The middle value = 254
So,
Median = 254Mode:The frequently occurring value in the data is known as mode.Mode in data:
The mode, here, is 202. (occurring 2 times.)
So,
Mode = 2\(\rule[225]{225}{2}\)
Assumptions: Tax depreciation is straight-line over three years. Pre-tax salvage value is 25 in Year 3 and 50 if the asset is scrapped in Year 2. Tax on salvage value is 40% of the difference between salvage value and book value of the investment. The cost of capital is 20%.
Answers
Based on the given assumptions and calculations, the net present value (NPV) of the investment in the new piece of equipment is -$27,045.76, indicating that the investment is not favorable.
To calculate the after-tax cash flows for each year and evaluate the investment decision, let's use the following information:
Assumptions:
Tax depreciation is straight-line over five years.
Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4.
Tax on salvage value is 30% of the difference between salvage value and book value of the investment.
The cost of capital is 12%.
Given:
Initial investment cost = $50,000
Useful life of the equipment = 5 years
To calculate the depreciation expense each year, we divide the initial investment by the useful life:
Depreciation expense per year = Initial investment / Useful life
Depreciation expense per year = $50,000 / 5 = $10,000
Now, let's calculate the book value at the end of each year:
Year 1:
Book value = Initial investment - Depreciation expense per year
Book value \(= $50,000 - $10,000 = $40,000\)
Year 2:
Book value = Initial investment - (2 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (2 \times$10,000) = $30,000\)
Year 3:
Book value = Initial investment - (3 \(\times\) Depreciation expense per year)
Book value = $50,000 - (3 \(\times\) $10,000) = $20,000
Year 4:
Book value = Initial investment - (4 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (4 \times $10,000) = $10,000\)
Year 5:
Book value = Initial investment - (5 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (5 \times $10,000) = $0\)
Based on the assumptions, the salvage value is $10,000 in Year 5.
If the asset is scrapped in Year 4, the salvage value is $15,000.
To calculate the tax on salvage value, we need to find the difference between the salvage value and the book value and then multiply it by the tax rate:
Tax on salvage value = Tax rate \(\times\) (Salvage value - Book value)
For Year 5:
Tax on salvage value\(= 0.30 \times ($10,000 - $0) = $3,000\)
For Year 4 (if scrapped):
Tax on salvage value\(= 0.30 \times ($15,000 - $10,000) = $1,500\)
Now, let's calculate the after-tax cash flows for each year:
Year 1:
After-tax cash flow = Depreciation expense per year - Tax on salvage value
After-tax cash flow = $10,000 - $0 = $10,000
Year 2:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $0 - $0 = $0
Year 3:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $0 - $0 = $0
Year 4 (if scrapped):
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $15,000 - $1,500 = $13,500
Year 5:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $10,000 - $3,000 = $7,000
Now, let's calculate the net present value (NPV) using the cost of capital of 12%.
We will discount each year's after-tax cash flow to its present value using the formula:
\(PV = CF / (1 + r)^t\)
Where:
PV = Present value
CF = Cash flow
r = Discount rate (cost of capital)
t = Time period (year)
NPV = PV Year 1 + PV Year 2 + PV Year 3 + PV Year 4 + PV Year 5 - Initial investment
Let's calculate the NPV:
PV Year 1 \(= $10,000 / (1 + 0.12)^1 = $8,928.57\)
PV Year 2 \(= $0 / (1 + 0.12)^2 = $0\)
PV Year 3 \(= $0 / (1 + 0.12)^3 = $0\)
PV Year 4 \(= $13,500 / (1 + 0.12)^4 = $9,551.28\)
PV Year 5 \(= $7,000 / (1 + 0.12)^5 = $4,474.39\)
NPV = $8,928.57 + $0 + $0 + $9,551.28 + $4,474.39 - $50,000
NPV = $22,954.24 - $50,000
NPV = -$27,045.76
The NPV is negative, which means that based on the given assumptions and cost of capital, the investment in the new piece of equipment would result in a net loss.
Therefore, the investment may not be favorable.
Please note that the calculations above are based on the given assumptions, and additional factors or considerations specific to the business should also be taken into account when making investment decisions.
For similar questions on assumptions.
https://brainly.com/question/15424356
#SPJ8
The complete question may be like :
Assumptions: Tax depreciation is straight-line over five years. Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4. Tax on salvage value is 30% of the difference between salvage value and book value of the investment. The cost of capital is 12%.
You are evaluating an investment in a new piece of equipment for your business. The initial investment cost is $50,000. The equipment is expected to have a useful life of five years.
Using the given assumptions, calculate the after-tax cash flows for each year and evaluate the investment decision by calculating the net present value (NPV) using the cost of capital of 12%.
35% of what is 28?............
Answers
35% of 80 is 28.
Answer is 80.
f(x)=−3x2+12x−11 Step 1 of 2 : Find all values of x that correspond to horizontal tangent lines. Select "None" if the function does not have any values of x that correspond to horizontal tangent lines.
Answers
Answer:
\(x = 2\) corresponds to a horizontal line tangent to \(f(x) = -3\cdot x^{2}+12\cdot x -11\).
Step-by-step explanation:
Let \(f(x) = -3\cdot x^{2}+12\cdot x -11\), its first derivative represents a formula to determine the slope of lines tangent to a given point of the curve and slopes of horizontal tangent line corresponds to those values of \(x\) such that \(f'(x) = 0\).
We obtain the first derivative and equalize it to zero:
\(-6\cdot x +12 = 0\)
And solve it for \(x\):
\(x = 2\)
\(x = 2\) corresponds to a horizontal line tangent to \(f(x) = -3\cdot x^{2}+12\cdot x -11\).

The ordered pair (2, 10) is a point on a direct variation equation. Write the direct variation equation.
Answers
Answer:
Y=KX so its 10=K2
Step-by-step explanation:
Plug in the Number OR K=y/x
Two points located on jk are j (-1,-9) and k (5,3). What is the slope of jk?
Answers
Answer:
2
Step-by-step explanation:
slope of line= \( \frac{y1 - y2}{x1 - x2} \)
slope of JK
\( = \frac{3 - ( - 9)}{5 - ( - 1)} \\ = \frac{3 + 9}{5 + 1} \\ = \frac{12}{6} \\ = 2\)
Answer:
Slope = 2
Step-by-step explanation:
Slope = \(\frac{rise}{run}\)
Slope = \(\frac{3+9}{5+1}\)
Slope = \(\frac{12}{6}\)
Slope = 2
A line passes though two points A(-2, 2). B(-1, 2). What is the slope:
Answers
Answer:
The slope is 0
Step-by-step explanation:
Slope = (y2 - y1) / (x2 - x1)
Where the values of x and y are from the known points
Here the points are (-2,2) and (-1,2)
So we have (x1,y1) = (-2,2) and (x2,y2) = (-1,2)
This means, x1 = -2 , x2 = -1 , y1 = 2 and y2 = 2
We now plug these values into the slope formula
Recall slope = (y2 - y1) / (x2 - x1)
==> plug in x1 = -2 , x2 = -2 , y1 = 2, y2 = 2
Slope = (2 - 2) / (-1 - (-2)
==> remove parenthesis
Slope = (2-2) / (-1 + 2)
==> simplify addition and subtraction
Slope = 0 / 1 = 0