An employee at a fireworks company is designing a rocket. The rocket will consist of a cardboard circular cylinder with a height that is seven times as large as the radius. On top of the cylinder will be a cone with a height of 5 in. and a radius equal to the radius of the base as shown in the figure. If the company wants to fill the cone and the cylinder with a total of 204 in.^3 of powder, then what should be the radius of the cylinder? Note that the volume of a right circular cylinder with radius r and height h is and the volume of a cone with a base of radius r and height h is .
Answers
The radius of the cylinder should be approximately 2.040 inches long.
How to calculate the radius of a rocket to contain a required quantity of powder
The volume required to store the powder is the sum of the volumes of the cylinder and the cone, whose expression is in this case:
204 in³ = (π/3) · r² · (4 in) + π · r² · h
204 in³ = (4/3 + h) · π · r²
204 in³ = (4/3 + 7 · r) · π · r²
204 = (4π/3) · r² + 7π · r³
7π · r³ + (4π/3) · r² - 204 = 0
The positive roots of the cubic equation are:
r ≈ 2.040 in
The radius of the cylinder should be approximately 2.040 inches long.
To learn more on volumes: https://brainly.com/question/1578538
#SPJ1

Related Questions
Leon took a total of 12 quizzes over the course of 2 weeks. How many weeks of school will Leon have to attend this quarter before he will have taken a total of 36 quizzes? Solve using unit rates.
Answers
Answer:
6 weeks.
Step-by-step explanation: Because if he answered 12 quizzes in 2 weeks then 12 times 3 equals 36 so then all you have to do is times the weeks by 3.
The measure of one small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles
Answers
Answer:
x + x - 45 = 90
2x - 45 = 90
2x = 135
x = 67.5, so x - 45 = 22.5
The other two angles measure 22.5° and 67.5°.
A student is assessing the correlation between the number of hours a plant receives sunlight and the height to which it grows. The table below shows the data:
Number of hours of sunlight
(x) 0 1 2 3 4 5 6 7 8 9
Height of plant in cm
(y) 4 7 10 13 16 19 22 25 28 31
Part A: Is there any correlation between the number of hours of sunlight that a plant receives and the height to which it grows? Justify your answer. (4 points)
Part B: Write a function which best fits the data. (3 points)
Part C: What does the slope and y-intercept of the plot indicate about the plant
Answers
Answer:
see below
Step-by-step explanation:
Part A
Notice that for each increase of 1 in x, there is an increase of 3 in y
There is a correlation between the amount of sunlight and the height of the plant
Part B
The slope in change in y over change in x
m = 3/1 = 3
y= mx+b
y = 3x+b
The y intercept is when x =0 so b = 4
y = 3x+4
Part C
With no sunlight the plant is 4 cm tall. As the plant gets more sunlight, the plant grows at 3 cm per hour of sunlight.
Step-by-step explanation:
there is a direct correlation between the hours of sunlight and the height of the plant.
a delta of 1 hour sunlight results consistently in a growth of 3 cm. there is not a single point in the set of data that deviates from this.
therefore, the function for the height of the plant based on the number of sunlight received is
y = 3x + 4
as every hour of sunlight (x) results in an additional growth of 3cm. and we are starting with a plant that is already 4 cm tall at the beginning (x=0).
the y-intercept is the first data point (x=0) and shows y=4.
the slope is 3 (or 3/1 as y/x ratio) indicating that with one hour of sunlight the plant grows an additional 3 cm.
and as mentioned, we started with a plant already 4cm tall.
X¹² - 1 แยกตัวประกอบของพหูนาม
Answers
Answer:
\(\left(x^2+1\right)\left(x+1\right)\left(x-1\right)\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4-x^2+1\right)\)
Step-by-step explanation:
Factor of \(x^{12}-1\) is
\(\left(x^2+1\right)\left(x+1\right)\left(x-1\right)\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4-x^2+1\right)\)
The mean salary offered to students who are graduating from Coastal State University this year is , with a standard deviation of . A random sample of Coastal State students graduating this year has been selected. What is the probability that the mean salary offer for these students is or less
Answers
Answer:
The probability that the mean salary offer is of X or less is the p-value of \(Z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\), in which \(\mu\) is the mean salary for the population, \(\sigma\) is the standard deviation for the population and n is the size of the sample.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Z-score with the Central Limit Theorem:
Z-is given by:
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
What is the probability that the mean salary offer for these students is X or less?
The probability that the mean salary offer is of X or less is the p-value of \(Z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\), in which \(\mu\) is the mean salary for the population, \(\sigma\) is the standard deviation for the population and n is the size of the sample.
15.
(4x +- 21)
(x - 23)

Answers
Answer:
4
2
−
1
1
3
+
4
8
3
Step-by-step explanation:
2021: Sales Revenues = $800,000. Cost of good sold = $350,000
2020: Sales Revenues = $795,000. Cost of good sold = $600,000
Answers
Answer:
Step-by-step explanation:
Sales Revenue: $800.00
Cost of good sold: $350,000.00
Subtract: $450,000.00
Sales Revenue: $795,000.00
Cost of good sold: $600,000.00
Subtract Sales $195,000.00
Revenue from Cost
of goods sold.
144 in the ratio 3:4
Answers
Answer: 132
Step-by-step explanation:
Evaluate 5x + 2y, if x = -1 and y = 0.
I need help fast!!!
Answers
2y is the same as 2*y
Now, we can plug the values of x and y into the equation and solve it, like this:
MENTAL MATH:
5 * (-1) = -5
2 * 0 = 0
FINALLY:
-5 + 0 = -5
what is 42,653 rounded to the nearest thousand?
Answers
Answer: The answer is 43000
Step-by-step: Adding a number under 500 to get 43000 makes it rounded up and not down.
What is the least common multiple of 18 and 22
Answers
Answer:
to find the least common multiple (LCM) of 18 and 22, you can use the following steps:
Prime factorize the numbers:
18 = 2 * 3^2
22 = 2 * 11
Identify the highest power of each prime factor that appears in either number:
The highest power of 2 is 2^1.
The highest power of 3 is 3^2.
The highest power of 11 is 11^1.
Multiply these highest powers together:
2^1 * 3^2 * 11^1 = 66.
Therefore, the least common multiple (LCM) of 18 and 22 is 66.
Step-by-step explanation:
A coal mine cost $972,000. The mine is estimated to hold 54,000 tons of coal and can be mined in 6 years. There is no residual value. During the first year of operations, 11,000 tons are extracted and sold. Calculate depletion expense for the first year.
Answers
Answer:
118,000
Step-by-step explanation:
1.003M x (6,000/51,000) = 118,000
If f(x) = 3x +5/x what is f(a+2)?
Answers
Substitute a+2 instead of x
That would look something like: 3(a+2)+5/a+2
Now simplify:
3a+6+5/a+2
3a+11/a+2
3(a+2) +5/(a+2)
3a+6 + 5/(a+2)
LCM: (3a(a+2) + 6(a+2) +5)/a+2
So your answer will be (3a^2 + 12a + 17)/(a+2)
I hope this helps :)
A linear function and a quadratic function both have a domain of all real numbers.
True
False
?
Answers
Answer: True
Explanation: The domain of a quadratic function in standard format is always all real numbers, meaning you can substitute any real number for x. The range of a function is the set of all real values of y that you can get by plugging real numbers into x.
Linear function is almost always going to be all real numbers. The range of a non-horizontal linear function is all real numbers no matter how flat the slope might look.
the range of the function shows all real values
Rename 3/10 and 2/3 using the least common denominator.
Answers
Answer:
LCD = 30
3/10 = 9/30
2/3 = 20/30
Step-by-step explanation:
This is the answer because:
1) First, the least common denominator is 30 because 10 x 3 is 30 and 3 x 10 is 30
2) Next, multiply the numerators with the same number you multiplied with the denominator
3 x 3 = 9
2 x 10 = 20
3) Therefore, the answers are:
3/10 = 9/30
2/3 = 20/30
Hope this helps!
write even number between 10 and 20
Answers
the radius r of the circle below is 11cm

Answers
Answer:
\({ \bf{area = \pi {r}^{2} }} \\ = 3.14 \times {11}^{2} \\ = 380.1 \: {cm}^{2} \)
Step 1: Rewrite equation
As the first step, it is helpful to rewrite the equation for the area of a circle. The a will stand for area, the π will stand for pi, and the r will stand for radius.
a= πr²
Step 2: Substitute numbers
For step 2, we will substitute information. We are made aware that the radius is 11, so we will replace r with 11. To make the equation easier to understand, we will add the multiplication sign in between pi and 11 squared.
a= π•11²
Step 3: Solve using PEMDAS
To solve this equation, we will follow the order of operations, also referred to as PEMDAS, standing for parentheses-exponent-multiplication-division-addition-subtraction. According to this formula, the first thing we will need to do is solve for the exponent. To do so, let’s find the squared value of 11.
a= π•11²
a= π•121
For the next part, we need to multiply 121 by π for the final answer. For the sake of this problem, we will leave pi as 3.14. This can always be replaced by putting the pi symbol into your calculator, though we will use 3.14.
a= 3.14•121
a= 379.94
This is your answer. Hope this helps! Comment below for more questions.
Find an equation of the plane.The plane through the point(4, −3, −1)and parallel to the plane 6x − y − z = 6
Answers
Both planes have the same normal vector:
\(6x-y-z=6\implies\mathbf n=\langle6,-1,-1\rangle\)
The plane we want must contain the point (4, -3, -1), so its equation would be
\(\mathbf n\cdot\langle x-4,y+3,z+1\rangle=0\)
\(\implies 6(x-4)-(y+3)-(z+1)=0\)
\(\implies\boxed{6x-y-z=28}\)
SoIve each equation. TWO of these are special cases ("no solution" and " all real numbers ".)4 (j-7) =127(2p +3 - 8 =6p +292 ( x-1) = 4+2x3(4c+5)=274(2k-6) +11 =8k -13

Answers
1.
\(\begin{gathered} 4\mleft(j-7\mright)=12 \\ 4j-28=12 \\ 4j=12+28 \\ 4j=40 \\ j=\frac{40}{4} \\ j=10 \end{gathered}\)2.
\(\begin{gathered} 7(2p+3)-8=6p+29 \\ 14p+21-8=6p+29 \\ 14p-6p=29-21+8 \\ 8p=16 \\ p=\frac{16}{8} \\ p=2 \end{gathered}\)3.
\(\begin{gathered} 2(x-1)=4+2x \\ 2x-2=4+2x \\ 2x-2x=4+2 \\ 0x=6 \\ no\text{ solution} \end{gathered}\)4.
\(\begin{gathered} 3(4c+5)=27 \\ 12c+15=27 \\ 12c=27-15 \\ 12c=12 \\ c=1 \end{gathered}\)5.
\(\begin{gathered} 4(2k-6)+11=8k-13 \\ 8k-24+11=8k-13 \\ 8k-8k=-13+24-11 \\ no\text{ solution} \end{gathered}\)(6x+9)/2=?
please help
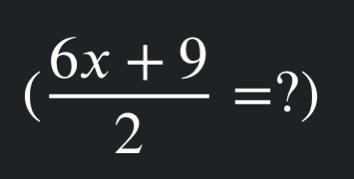
Answers
The value of x in the expression given is -7/6
Solving the given equation(6x + 9)/2 =
First step is to cross multiply
6x + 9 = 2
Collect like terms
6x = 2 - 9
6x = -7
divide both sides by 6 to isolate x
x = -7/6
Therefore the value of x in the expression given is -7/6
Learn more on equations: https://brainly.com/question/2972832
#SPJ1
Looking for the outcomes of A, B, C, and D. Thanks

Answers
In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data:
dice:
6 sided
Step 02:
outcomes:
Event A (odd):
1 , 3 , 5
outcomes = 3
Event B (5 or more):
5 , 6
outcomes = 2
Event C (≤ 3):
1 , 2 , 3
outcomes = 3
Event D (4):
4
outcomes = 1
Please help fast brainly will be given

Answers
Answer:
1. 500 milligrams
2. 6450 grams
3. 50 oranges
4. 30 weeks
5. 1500 grams
To do this, all you basically need to do is convert grams, milligrams, etc.
You also need to do Multiplying, Dividing, Adding, and Subtratcing.
Please give me Brainliest!
FUNCTIONS HW HELP NEEDED

Answers
a) The equation for Bueller's height above the ground as a function of time is: h(t) = 9 cos(πt/8) + 1.5
b) When Bueller has been on the ride for 1 minute and 30 seconds, his height above the ground is approximately 10.5 m.
What is a function?In mathematics, a function is a rule that assigns a unique output value to each input value in a specified set. More precisely, a function is a set of ordered pairs (x, y) where each x-value (the input) corresponds to exactly one y-value (the output).
In mathematics, an equation is a statement that asserts the equality of two expressions, typically containing one or more variables. An equation consists of two sides, the left-hand side, and the right-hand side, separated by an equal sign (=).
According to the given information,
a) To determine an equation for Bueller's height above the ground as a function of time, we can use the equation for the height of a point on a Ferris wheel:
h(t) = r cos(ωt) + h0
where:
1) h(t) is the height of the point above the ground at time t
2) r is the radius of the Ferris wheel
3) ω is the angular velocity of the Ferris wheel (in radians per second)
4) t is the time elapsed since the point was at its lowest position
5) h0 is the initial height of the point above the ground
In this case, we know that Bueller boards the Ferris wheel at a height of 1.5 m off the ground, so h0 = 1.5 m. The radius of the Ferris wheel is 9 m, and it rotates once every 16 seconds, so the angular velocity is:
ω = 2π / T = 2π / 16 = π / 8 radians per second
Therefore, the equation for Bueller's height above the ground as a function of time is:
h(t) = 9 cos(πt/8) + 1.5
b) To find Bueller's height off the ground when he has been on the ride for 1 minute and 30 seconds (or 90 seconds), we can substitute t = 90 into the equation for h(t):
h(90) = 9 cos(π(90)/8) + 1.5
h(90) = 9 cos(11.25π) + 1.5
Using a calculator, we get:
h(90) ≈ -6.3 m
Note that the negative sign means that Bueller is below ground level, which is not physically possible. This occurs because we started counting time from the bottom of the wheel, so 90 seconds corresponds to the bottom position plus 5 and a half rotations. To fix this, we can add a multiple of the period T = 16 seconds to t to bring it back to the correct range:
h(t) = 9 cos(πt/8) + 1.5
h(90 + 5T/2) = 9 cos(π(90 + 5T/2)/8) + 1.5
h(90 + 5T/2) = 9 cos(π(2 + 5/16)) + 1.5
h(90 + 5T/2) ≈ 10.5 m
Therefore, when Bueller has been on the ride for 1 minute and 30 seconds, his height above the ground is approximately 10.5 m.
To know more about the function visit:
brainly.com/question/30721594
#SPJ1
a coffee shop sells coffee beans by the pound. A container hold 16 kilograms of coffee beans. For every 1 kilogram, there are approximately 2.2 pounds
Answers
Answer:
23.6
Step-by-step explanation:
Answer: 23.6
Step-by-step explanation:
Leah learns that 2 more children will go on the trip. How can she modify
3(a + c) and 3a + 3c to include the cost of 2 more child passes?
Answers
By adding the cost of 2 child passes to each expression, Leah includes the cost of 2 more children going on the trip.
We have,
To include the cost of 2 more child passes in the expressions 3(a + c) and 3a + 3c,
We can simply add the cost of 2 child passes to each expression.
Let's assume the cost of each child pass is represented by the variable "p".
To modify 3(a + c), we add the cost of 2 child passes to the expression:
3(a + c) + 2p
This represents the total cost of 3 passes for children, including the original "a" and "c" passes, as well as the additional 2 passes.
To modify 3a + 3c, we also add the cost of 2 child passes:
3a + 3c + 2p
This represents the total cost of 3 passes for children, including the original "a" and "c" passes, as well as the additional 2 passes.
Thus,
By adding the cost of 2 child passes to each expression, Leah includes the cost of 2 more children going on the trip.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
F
G
H
J
If the diameter of a circle is 16 cm and the
intercepted arc length is 6m, what is the
measure of the central angle in radians?
3
8
3
7T
3
T
3²7
Answers
The measure of the central angle is 0.75 radians
How to solve an equation?An equation is an expression that can be used to show the relationship between two or more numbers and variables using mathematical operators.
The area of a figure is the amount of space it occupies in its two dimensional state.
The length of an arc with an angle of Ф is given by:
Length of arc = (Ф/360) * (π * diameter)
The diameter is 16 cm and intercepted arc length is 6 cm, hence:
Length of arc = (Ф/360) * (π * diameter)
6 = (Ф/360) * (π * 16)
Ф = 42.97°
Ф = 42.97° * π/180 = 0.75 radian
The measure of the central angle is 0.75 radians
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Danny’s home cost $350,000. If the federal government program for flood damage insurance covers only $150,000, what percent of the total value does this represent?
Answers
Amount of $150,000 represents 42.86% of $350,000.
What is Equation Modelling?
Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.
We have Danny’s home cost $350,000. The federal government program for flood damage insurance covers only $150,000.
Assume that it represents [x%] percent of the total value. Then, we can write -
x = (150000/350000) x 100
x = 42.86%
Therefore, $150,000 represents 42.86% of $350,000.
To solve more questions on equation modelling, visit the link below-
brainly.com/question/9144182
#SPJ1
How can you check if a line belongs to a plane (Cartesian equation of the line and the equation of the plane is given)?
Answers
For example, suppose you have the Cartesian equation of a line in the form:
y = mx + b
and the equation of a plane in the form:
ax + by + cz + d = 0
To check if the line belongs to the plane, you can substitute a point (x, y) on the line into the equation of the plane and solve for z. If the resulting value of z satisfies the equation of the plane, then the line belongs to the plane.
Here's an example:
Suppose the Cartesian equation of the line is y = 2x + 1, and the equation of the plane is 2x + 3y + 4z + 5 = 0.
If we substitute a point on the line, such as (1, 3), into the equation of the plane, we get:
2(1) + 3(3) + 4z + 5 = 0
Solving for z, we find that z = -1.5.
Since the resulting value of z satisfies the equation of the plane, the line belongs to the plane.
If the resulting value of z does not satisfy the equation of the plane, then the line does not belong to the plane.
income from operations of $231,000. In addition, it received interest income of $23,100 and received dividend income of $29,700 from another corporation. Finally, it paid $11,000 of interest income to its bondholders and paid $45,000 of dividends to its common stockholders. The firm's federal tax rate is 21%. What is the firm's federal income tax? Do not round intermediate calculations. Round your answer to the nearest dollar.
Answers
The firm's federal income tax is $57,168.
To calculate the firm's federal income tax, we need to determine its taxable income first. Taxable income is calculated by subtracting deductions from the firm's total income.
In this case, the firm's total income consists of income from operations, interest income, and dividend income.
Total income:
Income from operations = $231,000
Interest income = $23,100
Dividend income = $29,700
Total income = $231,000 + $23,100 + $29,700 = $283,800
Next, we deduct expenses from the total income. In this case, the only relevant expense is the interest paid to bondholders:
Total expenses = Interest paid to bondholders = $11,000
Taxable income = Total income - Total expenses = $283,800 - $11,000 = $272,800
Now, we can calculate the federal income tax by applying the federal tax rate of 21% to the taxable income:
Federal income tax = Taxable income * Federal tax rate
Federal income tax = $272,800 * 0.21 = $57,168
Therefore, the firm's federal income tax is $57,168.
For more such questions on tax,click on
https://brainly.com/question/28414951
#SPJ8
I need help plss dont lieplss and thank you

Answers
Answer:
B or C
hope this helps :)