An instrument vendor wants to sell new violin
bows and guitar picks. The vendor has
7 boxes of bows holding 45 bows in each
box. Boxes of picks contain 15 packages
with 60 picks in each package. If the vendor
wants to equally distribute all the bows and
picks to 5 local stores, how many of each
item will the stores receive?
Answers
Answer:
63 bows and 180 picks
Step-by-step explanation:
1. Find the total number of bows and picks.
7 boxes of 45 bows: 7 x 45 = 315 bows15 packages with 60 picks in each package: 15 x 60 = 900 picks2. Divide each number by the number of stores
315 bows / 5 stores = 63 bows per store900 picks / 5 stores = 180 picks per store15 x 60 = 900 then divide 900 by 5 = 180 picks
Have a nice day.
Related Questions
a spinner with three equal-sized sections marked A,B, and C is spun 100 times. the result of the experiment are shown in the table what is the experimental probability of landing on A on C
Answers
The experimental probability of landing on A is 0.3 and the experimental probability of landing on C is 0.4.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
To find the experimental probability of landing on A or C, we need to add up the number of times the spinner landed on A and C, and then divide that by the total number of spins.
From the table, we can see that the spinner landed on A 30 times and on C 40 times. Therefore, the total number of times the spinner landed on either A or C is:
30 + 40 = 70
So the experimental probability of landing on A or C is:
70/100 = 0.7
However, we need to find the experimental probability of landing on A or C separately. To do that, we need to divide the number of times the spinner landed on A or C individually by the total number of spins:
Experimental probability of landing on A = 30/100 = 0.3
Experimental probability of landing on C = 40/100 = 0.4
Therefore, the experimental probability of landing on A is 0.3 and the experimental probability of landing on C is 0.4.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
convert 195° from degrees to radians
Answers
13π/12 radians
1) We can convert this from degrees to radians following this formula, since 1º
\(\alpha^{\circ}\times\frac{\pi}{180^{\circ}}\)2) So, we can plug into that the given measure in degrees:
\(\begin{gathered} 195^{\circ}\times\frac{\pi}{180^{\circ}} \\ \frac{195\pi}{180}=\frac{13}{12}\pi\approx3.40 \end{gathered}\)Note that we rounded off to the nearest hundredth the value of pi.
3) Hence, the answer is approximately 3.40 radians or exactly 13/12
π
Which expression represents the amount of money John has collected?
John collects $5 for club dues from each member. Use the variable
m
for the number of members in the club.
Answers
Answer: The expression that represents the amount of money John has collected is:
5 * m
This expression calculates the amount of money John collects by multiplying the number of members (m) by the amount of money collected per member ($5).
Step-by-step explanation:
Please help fast! I will give brainliest. (number 5)

Answers
Answer:
B, 13.5
Step-by-step explanation:
Formula used is SA=4s^2
726= 4s^2
181.5= s^2
13.47=s
13.5~ s
need help please and thank you?!

Answers
Answer:
3. 50.27 inches squared
4. 113.1 km squared
Step-by-step explanation:
3. A=πr^2
π*16
4. A=πr^2
π*36
Have a good day :)
Answer:
1)50.3
2) 113
Step-by-step explanation:
I hope this helps!
What is the absolute value of –20?
Use the number line to answer the question.
Answers
forty samples of 100 are taken, with the total number of defective units being 150. what is the upper control limit of the three sigma (z
Answers
The upper control limit of the three-sigma process is approximately 3.807 defective units per sample.
To calculate the upper control limit (UCL) of the three-sigma (z) process, we first need to find the average number of defective units per sample and the standard deviation.
1. Calculate the average number of defective units per sample (p-bar):
Divide the total number of defective units (150) by the number of samples (40).
p-bar = 150 / 40 = 3.75 defective units per sample
2. Calculate the proportion of defective units (p) in each sample:
Divide the average number of defective units (3.75) by the sample size (100).
p = 3.75 / 100 = 0.0375
3. Calculate the standard deviation (σ) of the process using the formula:
σ = √(p * (1 - p) / n),
where n is the sample size.
σ = √(0.0375 * (1 - 0.0375) / 100)
= √(0.03609375 / 100) ≈ 0.0190
4. Calculate the three-sigma upper control limit (UCL) using the formula:
UCL = p-bar + 3 * σ
UCL = 3.75 + 3 * 0.0190 ≈ 3.75 + 0.057 ≈ 3.807.
For similar of questions on sigma.
https://brainly.com/question/28163163
#SPJ11
OMG HELP PLS IM PANICKING OMG OMG I GOT A F IN MATH AND I ONLY HAVE 1 DAY TO CHANGE MY GRADE BECAUSE TOMORROW IS THE FINAL REPORT CARD RESULTS AND I DONT WANNA FAIL PLS HELP-

Answers
Answer:
2/5 bucket
Step-by-step explanation:
1/2 and 3/4 are equal. So 2/5 is wrong.
hope this helped, and please mark as Brainliest <3
Suppose we know the prices of zero-coupon bonds for different maturities with par values all being $1,000. The price of a one-year zero coupon bond is $959.63; The price of a two-year zero- coupon bond is $865.20; The price of a three-year zero-coupon bond is $777.77; The price of a four-year zero-coupon bond is $731.74. What is, according to the liquidity performance hypothesis, the expected forward rate in the third year if ∆ is 1%? What is the yield to maturity on a three-year zero-coupon bond?
Answers
According to the liquidity preference hypothesis, the expected forward rate in the third year when ∆ is 1% is 12.18%, and the yield to maturity on a three-year zero-coupon bond is 10.35%.
According to the liquidity preference hypothesis, the interest rate for a long-term investment is expected to be equal to the average short-term interest rate over the investment period. In this case, the expected forward rate for the third year is stated as 4.28%.
To calculate the expected forward rate for the third year, we first need to calculate the prices of zero-coupon bonds for each year. Let's start by calculating the price of a four-year zero-coupon bond, which is determined to be $731.74.
The rate of return on a four-year zero-coupon bond is then calculated as follows:
Rate of return = (1000 - 731.74) / 731.74 = 0.3661 = 36.61%.
Next, we use the yield of the four-year zero-coupon bond to calculate the price of a three-year zero-coupon bond, which is found to be $526.64.
The expected rate in the third year can be calculated using the formula:
Expected forward rate for year 3 = (Price of 1-year bond) / (Price of 2-year bond) - 1
By substituting the values, we find:
Expected forward rate for year 3 = ($959.63 / $865.20) - 1 = 0.1088 or 10.88%
If ∆ (delta) is 1%, we can calculate the expected forward rate in the third year as follows:
Expected forward rate for year 3 = (1 + 0.1088) × (1 + 0.01) - 1 = 0.1218 or 12.18%
Therefore, according to the liquidity preference hypothesis, the expected forward rate in the third year, when ∆ is 1%, is 12.18%.
Additionally, the yield to maturity on a three-year zero-coupon bond can be calculated using the formula:
Yield to maturity = (1000 / Price of bond)^(1/n) - 1
Substituting the values, we find:
Yield to maturity = (1000 / $526.64)^(1/3) - 1 = 0.1035 or 10.35%
Hence, the yield to maturity on a three-year zero-coupon bond is 10.35%.
In conclusion, according to the liquidity preference hypothesis, the expected forward rate in the third year when ∆ is 1% is 12.18%, and the yield to maturity on a three-year zero-coupon bond is 10.35%.
Learn more about interest rate
https://brainly.com/question/28272078
#SPJ11
Help me solve this problem:
-3(x^-2 y^-2)^0
Answers
Answer:
\( = - 3\)
I have brainlest
I have follow me
I have heart and 5 star

PLEASE HELP FAST Looking for the bottom angle to find my answer! 30 POINTS

Answers
x = 242.7 m
Step-by-step explanation:
First we need to find the angle at one of the parachutists:
180 - 57 - 43 = 80°
We then use sine law to find the distance between the parachutists
\( \frac{x}{ \sin(57) } = \frac{285 \: m}{ \sin(80) } \)
Solving for x
\(x = (\frac{ \sin(57) }{ \sin(80) } )(285 \: m) = 242.7 \: m\)
Let R be the region bounded by the following curves Find the volume of the solid generated when R is revolved about the y-axis y=6x y=24 y=X,y= 6x,y= 24 Set up the integral that gives the volume of the solid. dy (Type exact answers_ The volume of the solid is (Type an exact answer) cubic units'
Answers
Answer:
\(V=4480\pi \text{ units}^3\)
Step-by-step explanation:
Rewrite the region in terms of x
\(\displaystyle x=\frac{y}{6},\,x=y,\,y=24\)
Identify inner and outer radii
The inner radius is \(\displaystyle r=\frac{y}{6}\) and the outer radius is \(R=y\) because as \(y\) goes from 0 to 24, \(x\) goes from \(\displaystyle x=\frac{y}{6}\) to \(x=y\) in that direction.
Perform Washer Method
\(\displaystyle V=\pi\int\limits^b_a {(R^2-r^2)} \, dy\\ \\V=\pi\int\limits^{24}_0 {\biggr(y^2-\biggr(\frac{y}{6}\biggr)^2\biggr)} \, dy\\\\V=\pi\int\limits^{24}_0 {\biggr(y^2-\frac{y^2}{36}\biggr)\biggr)} \, dy\\\\V=\pi\biggr(\frac{y^3}{3}-\frac{y^3}{108}\biggr)\biggr|_0^{24}\\\\V=\pi\biggr(\frac{24^3}{3}-\frac{24^3}{108}\biggr)\\ \\V=4480\pi \text{ units}^3\)
I've attached a visual to help better understand this problem!

This element orients readers by previewing the structure of the report.
O Definitions of key terms
O Organization
O Sources and methods
Answers
The element that orients readers by previewing the structure of the report is "Organization."
Organizing a report effectively helps readers understand the flow of information and the logical structure of the content. By providing an overview of the organization, readers can anticipate the main sections, their sequence, and the connections between them.
The organization element typically includes headings, subheadings, and a clear hierarchy of information. It outlines the main sections and subsections of the report, indicating how they are related and how they contribute to the overall message or argument.
In addition to the organization element, the other options listed—Definitions of key terms and Sources and methods—also play important roles in a report. Definitions of key terms clarify terminology and provide a common understanding, while Sources and methods explain the sources of information and the methods used in the report's research or analysis. However, in the context of previewing the structure, the Organization element specifically serves this purpose.
to learn more about organization click here:brainly.com/question/12825206
#SPJ11
This is 9th-grade math

Answers
An inequality for the graph above is y ≤ -3x + 6.
How to determine an equation of this line?In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):
y - y₁ = m(x - x₁)
Where:
x and y represent the data points.m represent the slope.First of all, we would determine the slope of this line;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (-3 - 6)/(3 - 0)
Slope (m) = -9/3
Slope (m) = -3
At data point (0, 6) and a slope of -3, a linear equation for this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y - 6 = -3(x - 0)
y = -3x + 6
y ≤ -3x + 6 (since the solid line is shaded below).
Read more on point-slope here: brainly.com/question/24907633
#SPJ1
Can someone please check if I did it right, thank you. <3

Answers
Answer:
Please see below.
Step-by-step explanation:
Original equation:
2x - y = 5
If you were to move the 2x to the other side of the equation, y would still be negative.
-y = -2x + 5
Now, if you wanted y to be positive, you would divide both sides by -1.
y = 2x - 5
Please let me know if I'm incorrect and I'll edit the question :)
need help for one more question

Answers
Answer:
1/2
Step-by-step explanation:
If you convert all the fractions to having 16 at the bottom, you will get 12/16,
11/16,10/16,9/16...
Notice that the top is decreasing by 1 every time so the next number will be 8/16
8/16 is not in simplest form so convert that to 1/2
Given that p(x) = 2(x - 12)2 + 5, what is the value p(3)
Answers
Answer:
p(3) = 25
Step-by-step explanation:
p(3) = 2(3 - 12)2+5
p(3) = 6 - 24 + 2 + 5
p(3) = 25
find a set of parametric equations for the rectangular equation that satisfies the given condition. (enter your answers as a comma-separated list.)y = x2, t = 6 at the point (6, 36)
Answers
The set of parametric equations for the rectangular equation y = x^2 that satisfies the condition t = 6 at the point (6, 36) is x = t and y = t^2.
To find a set of parametric equations for the rectangular equation y = x^2 that satisfies the condition t = 6 at the point (6, 36), we can use the following steps:
Start with the equation y = x^2.
Introduce a parameter, let's say t, to represent the x-coordinate.
Express x and y in terms of t. Since y = x^2, we substitute x with t to get y = t^2.
Now, we need to find the values of t that correspond to the given condition t = 6 at the point (6, 36). To do this, we set t = 6 and find the corresponding value of y.
When t = 6, y = (6)^2 = 36. So, the point (6, 36) satisfies the equation y = x^2 with t = 6.
Finally, we can write the set of parametric equations as follows:
x = t
y = t^2
Therefore, the set of parametric equations for the rectangular equation y = x^2 that satisfies the condition t = 6 at the point (6, 36) is x = t and y = t^2.
These parametric equations allow us to represent the relationship between x and y in terms of the parameter t. By varying the value of t, we can generate different points on the curve y = x^2. In this case, when t = 6, we obtain the point (6, 36) on the curve.
Learn more about parametric equations here
https://brainly.com/question/30451972
#SPJ11
What is the value of Angle 'a'?
a
47°
Answers
Answer:
133
Step-by-step explanation:
180-47=133
Answer: if the shape is a triangle, 180-47=133
if it is any other shape, 360-47=313
Step-by-step explanation:
What is the answer ?????

Answers
Step-by-step explanation:
very difficult............
Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the curves y=x2, y=0, x=1, and x=2 about the line x=4.
Answers
Volume of the solid obtained by rotating the region is 67π/6 .
Given,
Curves:
y=x², y=0, x=1, and x=2 .
The arc of the parabola runs from (1,1) to (2,4) with vertical lines from those points to the x-axis. Rotated around x=4 gives a solid with a missing circular center.
The height of the rectangle is determined by the function, which is x² . The base of the rectangle is the circumference of the circular object that it was wrapped around.
Circumference = 2πr
At first, the distance is from x=1 to x=4, so r=3.
It will diminish until x=2, when r=2.
For any given value of x from 1 to 2, the radius will be 4-x
The circumference at any given value of x,
= 2 * π * (4-x)
The area of the rectangular region is base x height,
= \(\int _1^22\pi \left(4-x\right)x^2dx\)
= \(2\pi \cdot \int _1^2\left(4-x\right)x^2dx\)
= \(2\pi \left(\int _1^24x^2dx-\int _1^2x^3dx\right)\)
= \(2\pi \left(\frac{28}{3}-\frac{15}{4}\right)\)
Therefore volume of the solid is,
= 67π/6
Know more about volume of solids,
https://brainly.com/question/23705404
#SPJ4
PLZZZZZZ HELP 20 POINTS
In a recent year, 33.8% of all registered doctors were female. If there were 54,300 female registered doctors that year, what was the total number of registered doctors?
Round your answer to the nearest whole number.
Answers
Answer:
160 650.88 ( rounds to 160 651)
Step-by-step explanation:
Let n be the total amount of registered doctors that year. Then:
0.338n=54300
n=54300/0.338= 160 650.88 ( rounds to 160 651)
12 out of 20 students prefer having a study hall. What percentage of students prefer study hall?
Answers
Your answer is the question
Answer:
2.4 %
Step-by-step explanation:
magic *poof*
a(n) ? is a shorthand method for writing a mathematical rule.a. equal sign (=)b. equationc. formulad. math problem
Answers
The equation is a shorthand method for writing a mathematical rule.
The answer to your question is b.equation. An equation is a shorthand method for writing a mathematical rule. It represents a relationship between two or more variables using mathematical symbols and operations. Equations are commonly used in algebra, calculus, and other areas of mathematics to solve problems and make predictions. They are written using an equal sign (=) to show that the expression on the left is equal to the expression on the right. Equations are an important tool in mathematics because they allow us to express complex ideas in a concise and precise way. By using equations, we can simplify calculations and solve problems more efficiently.
Visit here to learn more about the mathematical rule:
brainly.com/question/15502489
#SPJ11
Divide. Write your answer as a fraction in simplest form.
−4/11 ÷ 2/7=
Answers
Answer:
-14/11
Step-by-step explanation:
when dividing a fraction, you flip the second fraction and turn the division sign into multiplication
so now you have -4/11 x 7/2
4 is divisible by 2 so you have: -2/11 x 7/1
now multiply -2 with 7 and 11 with 1: -14/11
i'm stuck on this problem!
7x-7;x=4
Answers
Answer:
7x-7 ;x=4
we will just substitute for the values
=7(4)-7
=28-7
=21
Step-by-step explanation:
award as brainliest
Which could be an equation of the trend line shown in graph?
A. y = 6x + 12
B. y = 8x + 15
C. y = 6x + 6
D. y = 8x + 8
Answers
Answer C
Step-by-step explanation:.
Solve for height using the tangent method. Show your work.
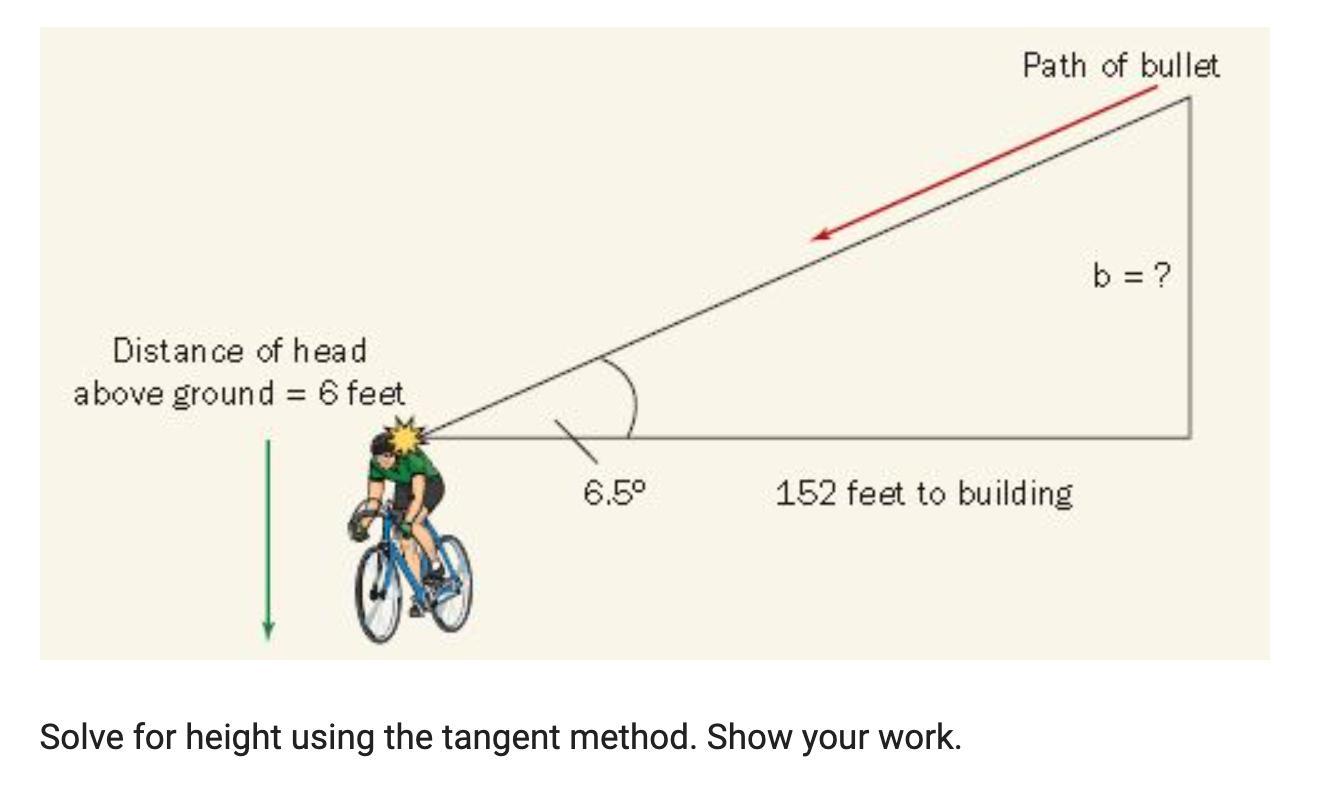
Answers
Answer:
b = 17.318 height = 23.318 ft
Step-by-step explanation:
This IS very similar to the other one, Emily..... Have you tried to solve it the same way?
b = 152 tan 6.5 = 17.318 ft (using a calculator)
add the height of the victim's head (6 ft)
17.318 + 6 = 23.318 ft
Which statement about the graph of y=12·(1/2)x is true?

Answers
The graph has an asymptote at y = 0.
Option (A) is correct.
What is the asymptote of the graph?
An asymptote is a straight line that constantly approaches a given curve but does not meet at an infinite distance. In other words, an Asymptote is a line that a curve approaches as it moves toward infinity.
The given function is:
\(y = 12.(\frac{1}{2})^x\)
Now let's draw the graph for this given function,
By observing the graph we can conclude that the graph has an asymptote at y = 0 cause it is not meeting to the x-axis when it is approaching infinity.
Hence, the graph has an asymptote at y = 0.
To learn more about asymptote of the graph, visit:
https://brainly.com/question/10712512
#SPJ1

which number sentence is true?a.12 < |-12|b.|-12| < |-48|c.|-48| < |48|d.|12| > |-48|
Answers
The correct number sentence is d. |12| > |-48|. This means that the absolute value of 12 is greater than the absolute value of -48.
Absolute value represents the distance of a number from zero on the number line. In option a, 12 is less than the absolute value of -12, which is 12. This is not true because 12 is not less than 12. In option b, the absolute value of -12 is 12, and it is indeed less than the absolute value of -48, which is 48. Therefore, option b is also false.
Moving on to option c, the absolute value of -48 is 48, and it is not less than the absolute value of 48, which is also 48. This means that option c is false as well.
Finally, in option d, the absolute value of 12 is 12, and it is greater than the absolute value of -48, which is 48. Hence, option d is the only true statement among the given options.
To summarize, the correct number sentence is d. |12| > |-48|, as the absolute value of 12 is greater than the absolute value of -48.
Learn more about Absolute value
brainly.com/question/4691050
#SPJ11