An ounce of gold costs $1310 and an ounce of silver costs $20. Find all possible weights of
silver and gold that make an alloy (combination of metals) that costs less than $900.
s = number of ounces of silver
g = number of ounces of gold
Find the inequality for this question
Answers
By using linear inequation it can be calculated that-
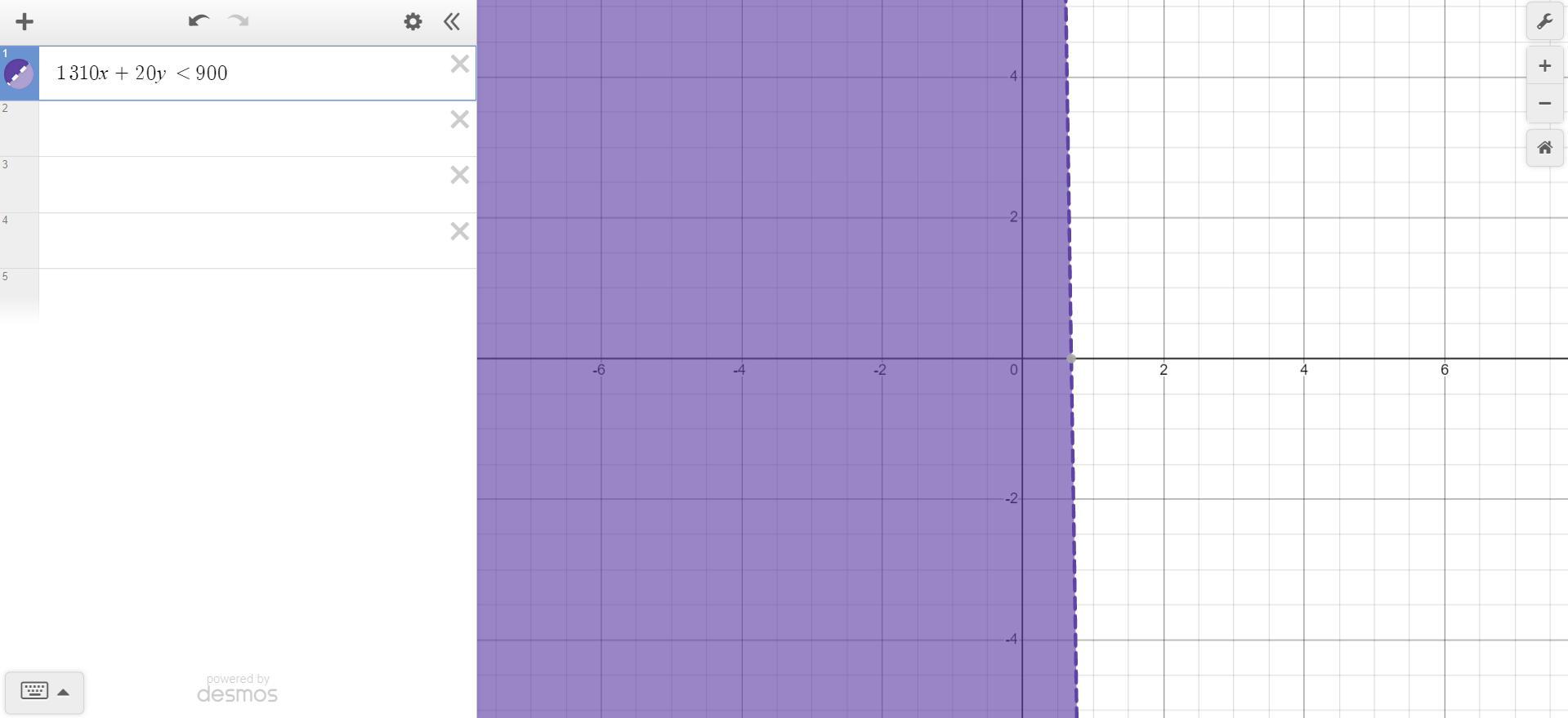
The shaded region right of the y axis and above the x axis gives all possible solution.
The required linear inequation is
1310g + 20s < 900
What is linear inequation?
Inequation shows the comparision between two algebraic expressions by connecting the two algebraic expressions by >, <, ≥, ≤
A one degree inequation is known as linear inequation
Let the alloy has g ounces of gold and s ounces of silver
An ounce of gold costs $1310 and an ounce of silver costs $20.
Cost of the alloy should be less than $900
The required linear inequation is
1310g + 20s < 900
The graph has been attached
The shaded region right of the y axis and above the x axis gives all possible solution.
To learn more about linear inequation, refer to the link-
https://brainly.com/question/25799000
#SPJ1
Related Questions
What is 38,050,000 expressed in scientific notation?А. 3.805 x 108ОООв. 0.3805 x10^8С. 0.38 х 10-8D. 3 805 x 107
Answers
By definition, Scientific Notation has the following form:
\(a\cdot10^b\)Where "a" is a number greater than or equal to 1, but less than 10 and "b" is an Integer.
In this case, you have this number:
\(38,050,000\)To express it in Scientific notation, follow these steps:
-The decimal point must be after the first digit (which must not be zero), so you must move de the decimal point 7 spaces to the left, so "b" will be positive.
-Then, the exponent "b" will be 7.
So, you get 38,050,000 expressed in scientific notation is :
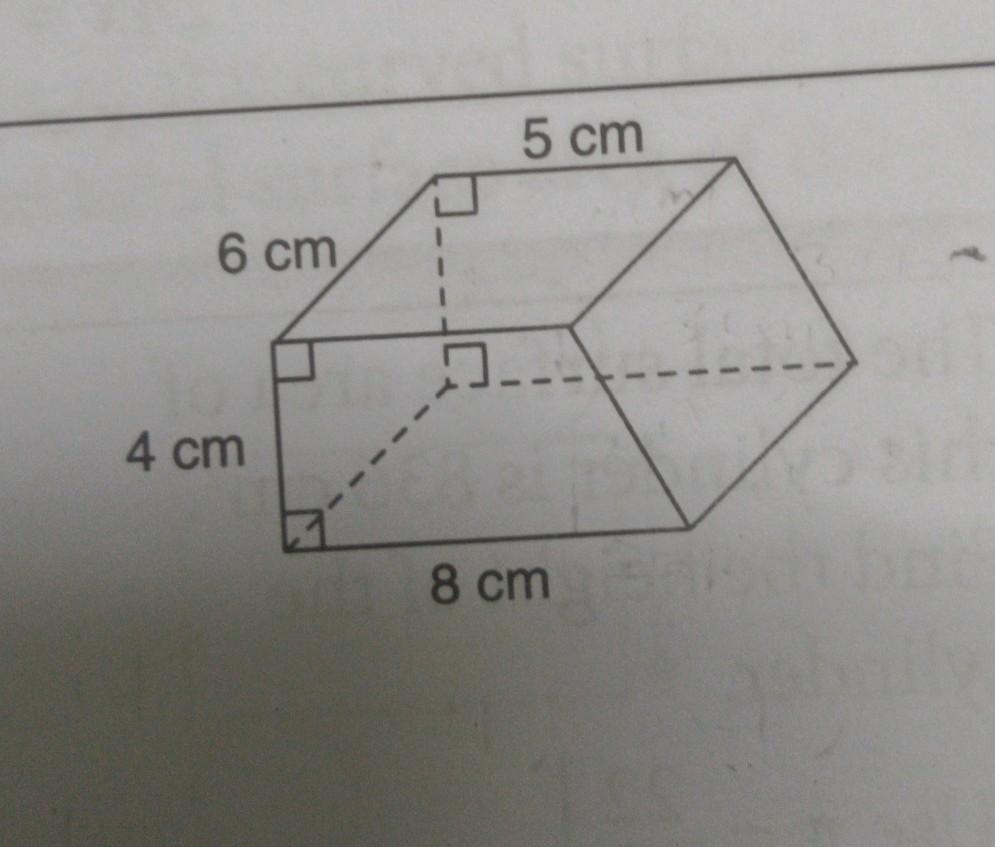
\(=3.805\cdot10^7\)find the surface area of each of these solid (useπ 22)
__
7
Answers
Answer:
156 cm³
Step-by-step explanation:
The solid is a prism with a trapezoid base.
volume = (area of base) × height
V = (8 cm + 5 cm)(1/2)(4 cm) × 6 cm
V = 156 cm³
Ms Davis is doing an activity with her statistic students where she gives them a 20 question multiple top choice test and they know none of the answers. Students need to guess on every question and each question has 5 possible choices, 1 of the which is correct.
What is the mean and standard deviation of the number of questions that each student gets correct?
Answers
Answer:
The mean and standard deviation of the number of questions that each student gets correct are 4 and 1.789 respectively.
Step-by-step explanation:
Let the random variable X be defined as the number of correct answers marked by a student.
It is provided that each question has 5 possible choices, 1 of the which is correct.
Then the probability of marking thee correct option is:
\(P(X)=\frac{1}{5}=0.20\)
There are a total of n = 20 questions to be answered.
As the students does not the answer to any question, they would be guessing for each question. This implies that for a random question, all the five options has the equal probability of being correct and each of the five options can be correct independently from the other.
All these information above indicates that the random variable X follows a Binomial distribution with parameters n = 20 and p = 0.20.
The mean and standard deviation of a Binomial distribution are:
\(\mu=np\\\\\sigma=\sqrt{np(1-p)}\)
Compute the mean and standard deviation of the random variable X as follows:
\(\mu=np=20\times 0.20=4\\\\\sigma=\sqrt{np(1-p)}=\sqrt{20\times 0.20\times(1-0.20)}=1.789\)
Thus, the mean and standard deviation of the number of questions that each student gets correct are 4 and 1.789 respectively.
According to the question,
The probability of making 3 correct options will be:
→ \(P(X) = \frac{1}{5}\)
\(= 0.20\)
Total number of questions,
n = 20As we know,
The mean will be:
→ \(\mu = np\)
By substituting the values, we get
\(= 20\times 0.20\)
\(= 4\)
and,
The standard deviation will be:
→ \(\sigma = \sqrt{np(1-p)}\)
\(= \sqrt{20\times 0.20\times (1-0.20)}\)
\(= 1.789\)
Thus the responses above are correct.
Learn more about standard deviation here:
https://brainly.com/question/20896613
"quadrilateral ABCD is similar to quadrilateral QRST"\( \frac{rs}{bc} \frac{?}{dc} \)
!["quadrilateral ABCD is similar to quadrilateral QRST"[tex] \frac{rs}{bc} \frac{?}{dc} [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/X54DPXPyVZvLmmxGDPQEqSKmwDyCMQ78.jpeg)
Answers
Let's take the ratio of the sides
Using proportion,
5/10 = 4/x
cross-multiply
5x = 40
Divide both-side of the equation by 5
x = 8
Teresa bought 6 CDs that were each the same price. Including sales tax, she paid a total of 84.60 . Each CD had a tax of 0.80 . What was the price of each CD before tax?
Answers
Answer:0.70
Step-by-step explanation:
Note: Enter your answer and show all the steps that you use to solve this problem in the space provided.
Does the series converge or diverge? If it converges, what is the sum? Show your work.

Answers
Step-by-step explanation:
This is a geometric series where our common ratio is -1/2, and a is -4
Since r is less than -1, this series converges so
The sun is
\( \frac{ - 4}{1 + 0.5} \)
\( \frac{ - 4}{1.5} = - \frac{8}{3} \)
The sum is -8)3
A gym member tracked his weight. In the first week he gained 2 pounds. In the second week, he lost 5. In the third week, he lost 2 more. What was his overall change in weight?
Answers
A full can of paint contains 4/5 of a gallon. Brandon used 3/4 of a can of paint to paint a doghouse. He then used 2/3 of what remained in the can to paint a door. How much paint is left in the can,in gallons?
Answers
Answer:
1/60 gallon
Step-by-step explanation:
You want to know what is left of 4/5 gallon of paint if 3/4 gallon was used to paint a doghouse, and 2/3 of the remaining amount was used to paint a door.
Amount remainingTo find the amount remaining we subtract the amount used for the doghouse from the original amount:
4/5 -3/4 = (16 -15)/20 = 1/20 . . . . . gallon
2/3 of that was used, so 1/3 of it remains:
(1/3)(1/20 gallon) = 1/60 gallon
There is 1/60 of a gallon of paint left in the can.
__
Additional comment
In a standard size gallon paint can, that's about 0.11 inches of paint in the bottom.
<95141404393>

Tracy goes on a 3 day and night school band trip. There is no cost for travel and each band member only pays half
Answers
Answer:
D 9%
Explanation
A cell site is a site where electronic communications equipment is placed in a cellular network for the use of mobile phones. The numbers y of cell sites from 1985 through 2011 can be modeled byy = 269573/1+985e^-0.308t where t represents the year, with t = 5 corresponding to 1985. Use the model to find the numbers of cell sites in the years 1998, 2003, and 2006.
Answers
Answer:
(a) 3178
(b) 14231
(c) 33152
Step-by-step explanation:
Given
\(y = \frac{269573}{1+985e^{-0.308t}}\)
Solving (a): Year = 1998
1998 means t = 8 i.e. 1998 - 1990
So:
\(y = \frac{269573}{1+985e^{-0.308*8}}\)
\(y = \frac{269573}{1+985e^{-2.464}}\)
\(y = \frac{269573}{1+985*0.08509}\)
\(y = \frac{269573}{84.81365}\)
\(y = 3178\) --- approximated
Solving (b): Year = 2003
2003 means t = 13 i.e. 2003 - 1990
So:
\(y = \frac{269573}{1+985e^{-0.308*13}}\)
\(y = \frac{269573}{1+985e^{-4.004}}\)
\(y = \frac{269573}{1+985*0.01824}\)
\(y = \frac{269573}{18.9664}\)
\(y = 14213\) --- approximated
Solving (c): Year = 2006
2006 means t = 16 i.e. 2006 - 1990
So:
\(y = \frac{269573}{1+985e^{-0.308*16}}\)
\(y = \frac{269573}{1+985e^{-4.928}}\)
\(y = \frac{269573}{1+985*0.00724}\)
\(y = \frac{269573}{8.1314}\)
\(y = 33152\) --- approximated
Translate to an equation please.
four less than thirteen times a number is equal to that number added to eight
Answers
Hi
let call "a number" X.
then we have: 4-13X = X + 8 ..
13x-x = 8+ 4
12x= 12
X= 1
A truck can be rented from Company A for $100 a day plus $0.30 per mile. Company B charges $50 a day plus $0.80 per mile to rent the same truck. Find the number of miles in a day at which the
rental costs for Company A and Company B are the same.
Atmiles, the rental costs are the same from either company.
Answers
Answer:
100 miles
Step-by-step explanation:
Let m be the number of miles.
\(100 + .30m = 50 + .80m\)
\(100 = 50 + .50m\)
\(.50m = 50\)
\(m = 100\)
Answer:
100
Step-by-step explanation:
You can put into a graph such as desmos and see where the lines intersect. the x value of the intersection is the answer you want.

which system of equations has two solutions?

Answers
The system of equations plotted on graph 3 has two solutions.
In the given figure, three different parabola and lines are drawn.
The intersection of the parabola and the line represent the solution of that system of equations.
Graph 1:
The parabola and the line do not intersect at each other.
Therefore, the equation has no solution.
Graph 2:
The parabola and the line intersect each other at one point, that is (1, 1).
Therefore, the equation has one solution.
Graph 3:
The parabola and the line intersect each other at two points that is (4, 1) and (0.5, -1).
Therefore, the equation has two solutions.
Therefore, the system of equations plotted on graph 3 has two solutions.
Learn more about system of equations here:
brainly.com/question/15362774
#SPJ1
Answer:
c
Step-by-step explanation:
third graph
Solve by Factoring:
2x^2 - x - 3 = 0
Answers
Answer:
x = 3/2 or x = -1
Step-by-step explanation:
2x² - x - 3 = 0
2*(-3) = -6
Factors of -6:
(-1, 6), (1, -6), (-2, 3), (2, -3)
We need to find a pair that adds up to the co-eff of x which is (-1)
Factors :(2,-3)
2 - 3 = -1
so, 2x² - x - 3 = 0 can be written as:
2x² + 2x - 3x - 3 = 0
⇒ 2x(x + 1) -3(x + 1) = 0
⇒ (2x - 3)(x + 1) = 0
⇒ 2x - 3 = 0 or
x + 1 = 0
⇒ 2x = 3 or x = -1
⇒ x = 3/2 or x = -1
Some students are planning to sell gourmet popcorn at a school fundraiser. They plan to offer cheese popcorn and peanut butter popcorn. The table shows the cost of the ingredients for each type of popcorn and the price at which the students plan to sell the popcorn.
The students want to make and sell 100 containers of popcorn. They can spend at most $50 for the ingredients for each type of popcorn and the price at which the students plan to sell the popcorn.
Answers
Answer : 5 Step-by-step explanation:
Which of the following values have 2 significant figures? Check all that apply.A. 45 B. 90C. 180D. 22.5
Answers
To find the 2 significant figures:
A. 45
Since, there are two non zeros 4 and 5.
Therefore, this has 2 significant figures.
B. 90
Since, it has only one non zero digit 9.
Therefore, it has not 2 significant figures.
C. 180
Since, there are two non zeros 1 and 8.
Therefore, this has 2 significant figures.
D. 22.5
Since, there are three non zeros 2, 2 and 8.
Therefore, this has not 2 significant figures.
Hence, the correct options are A and C.
Which explains whether or not the graph represents a direct variation?

Answers
Answer:
The slope is 3 and equation of the line is y=3x. I think the answer is the 1st option
Step-by-step explanation:
Given:
y=3x
Direct variation equations have the form:
y=kx,
where
k is the constant of proportionality
so k=3
A corporation creates a sinking fund in order to have $900,000 to replace some machinery in 10 years. How much should be placed in this account at the end of each month if the annual interest rate is 3.8% compounded monthly? (Round your answers to the nearest cent.) How much interest was earned during the third month of the 7th year?
Answers
The interest earned during the third month of the 7th year is $3,613.55.
What is interest rate?
The amount of interest due each period expressed as a percentage of the amount lent, deposited, or borrowed is known as an interest rate.
Let PMT be the monthly payment, r be the monthly interest rate, and n be the total number of payments. Then:
FV = PMT × [(1 + r)n - 1]/r
In this case, we want to find PMT, given that FV = $900,000, r = 0.038/12, and n = 10 × 12 = 120:
\($900,000 = PMT * {[(1 + 0.038/12)}^{120} - 1]/(0.038/12)\)
Solving for PMT, we get:
PMT = $682.48
\(FV = $682.48 * [(1 + 0.038/12)^87 - 1]/(0.038/12)\\\\ = $89,324.47\\\\PV = $682.48 * [(1 + 0.038/12)^83 - 1]/(0.038/12) \\\\= $85,710.92\)
The interest earned during the third month of the 7th year is:
$89,324.47 - $85,710.92 = $3,613.55
Therefore, the interest earned during the third month of the 7th year is $3,613.55.
To know more about interest rate? visit,
https://brainly.com/question/25793394
#SPJ1
Match each value to what it represents. 25 = 32 1. 32 power 2. 5 exponent 3. 2 base

Answers
Answer:
The power is 32 because that is what 2 to th 5 is , 2 is the base as its the number being multiplied 5 times which leaves 2 as the exponent.
What is 5x6 + (5x5-5) to the 2nd power
Answers
Answer: 2500
Step-by-step explanation: If you calculate out 5x6 that equals 30 and 5x5-5 equals 20, when you do 30+20 that equals 50 and 50 to the 2nd power is 50x50 and that would equal 2500
During one year, a family made 8 trips to the museum. The distance from their house to the 47 is miles. How many miles did the family drive in 8 trips?
Answers
Answer:
376
Step-by-step explanation:
47 times 8 would be the number of miles that the family took in 8 trips.
Statistical data of breakdowns of computer XXX show that the duration for trouble-free operation of the machine can be described as a gamma distribution with a mean of 40 days and a standard deviation of 10 days. The computer is occasionally taken out for maintenance in order to insure operational condition at any time with a 95% probability.
1. How often should the computer be scheduled for maintenance? Should it be shorter or longer than the mean of 40 days?
2. Three XXX computers were acquired at the same time by an engineering consulting firm. The computers are operating under the same environment, workload, and regular maintenance schedule. The breakdown times between the computers, however, may be assumed to be statistically independent. What is the probability that at least one of the three machines will break down within the first scheduled maintenance time?
Answers
1. In this case, we want the reliability to be 95%, so the probability of not breaking down is 0.95.
2. Probability of no breakdowns = (reliability of a single machine)^3. Probability of at least one breakdown = 1 - Probability of no breakdowns
1. To determine how often the computer should be scheduled for maintenance, we need to consider the reliability and the desired level of operational condition. Since the duration for trouble-free operation follows a gamma distribution with a mean of 40 days, this means that, on average, the computer can operate for 40 days before a breakdown occurs.
To ensure operational condition with a 95% probability, we can calculate the maintenance interval using the concept of reliability. The reliability represents the probability that the machine will not break down within a certain time period. In this case, we want the reliability to be 95%, so the probability of not breaking down is 0.95.
Using the gamma distribution parameters, we can find the corresponding reliability for a specific time duration. By setting the reliability equation equal to 0.95 and solving for time, we can find the maintenance interval:
reliability = 0.95
time = maintenance interval
Using reliability and the gamma distribution parameters, we can calculate the maintenance interval.
2. To calculate the probability that at least one of the three machines will break down within the first scheduled maintenance time, we can use the complementary probability approach.
The probability that none of the machines will break down within the first scheduled maintenance time is given by the reliability of a single machine raised to the power of the number of machines:
Probability of no breakdowns = (reliability of a single machine)^3
Since the breakdown times between the machines are statistically independent, we can assume that the reliability of each machine is the same. Therefore, we can use the reliability calculated in the first part and substitute it into the formula:
Probability of at least one breakdown = 1 - Probability of no breakdowns
By calculating this expression, we can determine the probability that at least one of the three machines will break down within the first scheduled maintenance time.
For more such questions on Probability
https://brainly.com/question/23286309
#SPJ8
Find the complete factored form of the
polynomial :
-8m²n-7m² nª
Enter the correct answer.
Answers
The polynomial -8m²n - 7m²n can be factored using the common factor -m²n. The complete factored form of the polynomial is (-m²n) (8 + 7a).
To find the complete factored form of the polynomial -8m²n - 7m²n, we can factor out common terms from both the terms. The common factor in the terms -8m²n and -7m²n is -m²n. We can write the polynomial as:
-8m²n - 7m²n = (-m²n) (8 + 7a)
Therefore, the complete factored form of the polynomial -8m²n - 7m²n is (-m²n) (8 + 7a). This expression represents the original polynomial in a multiplied form. We can expand this expression using distributive law to verify that it is equivalent to the original polynomial.
For more such questions on polynomial, click on:
https://brainly.com/question/1600696
#SPJ8
Kathryn invests $8,327 in a savings account with a
fixed annual interest rate compounded continuously. After
10 years, the balance reaches $18,532.08. What is the
interest rate of the account?
Answers
Answer:
Below
Step-by-step explanation:
The equation to use for CONTINUOUS compounding is :
FV = PV e^(it)
18532.08 = 8327 * e^( i*10) where i is the interest in decimal form
18532.08/8327 = e^(10i)
2.225541 = e^(10i) now take natural log (ln) of both sides to get
.8000 = 10i
i = .08 or 8% interest
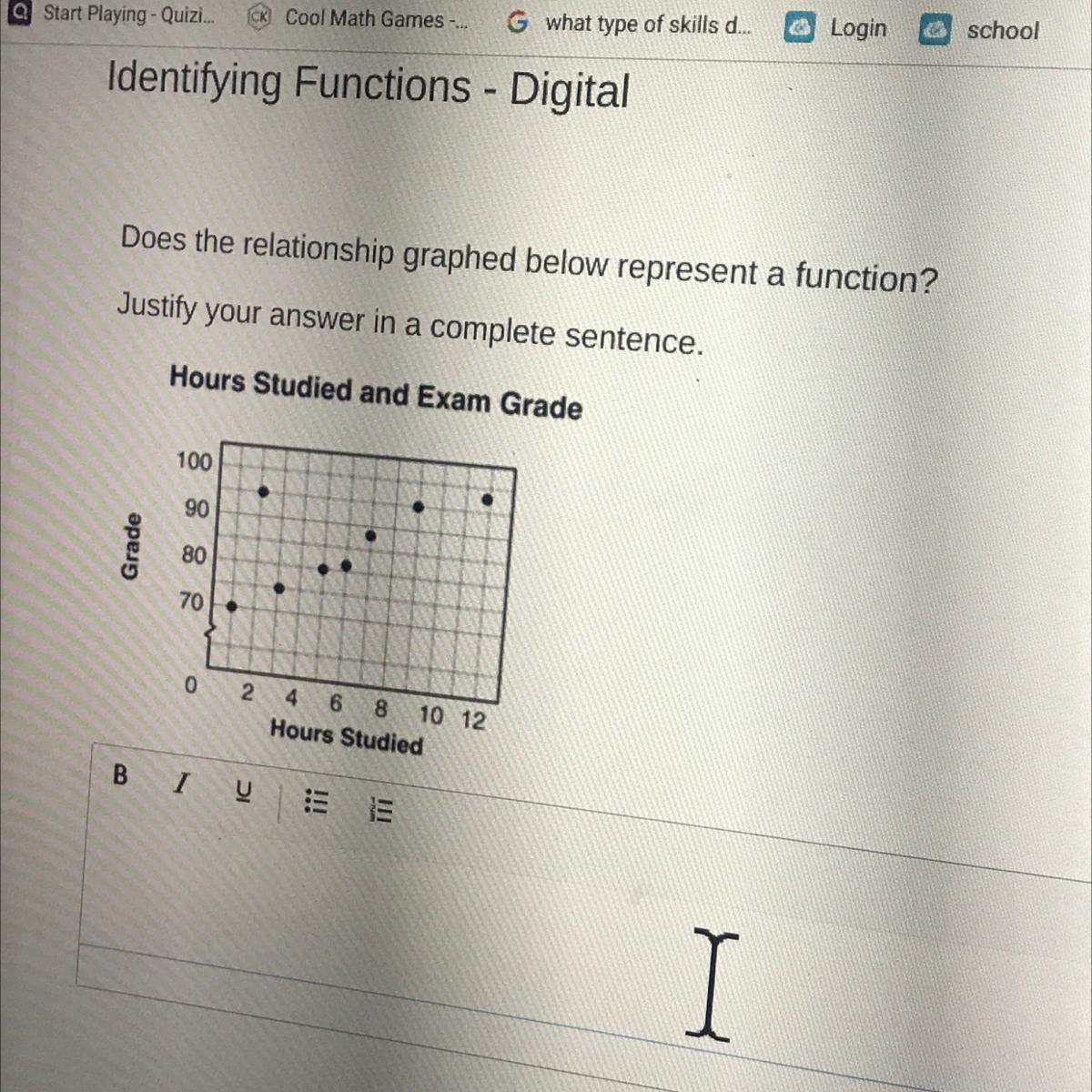
Someone help how do I find if it’s a function
Answers
To know if this is a function, simply perform a vertical line test on it.
If it passed the vertical line test then it is a function but if it fails it then it is not a function
In the graph given, if you draw a vertical point at any point, we woulld not have two points on the vertical line, hence it is a function
What is the length of AC in the given triangle?

Answers
The length of AC in the given triangle is 126.6.
The length of AC in the given triangle can be calculated using the Pythagorean Theorem. The length of AC is the hypotenuse of the right triangle, and can be calculated by taking the square root of the sum of the squares of the other two sides of the triangle. In this case, the length of AC is equal to the square root of (b² + 99.6²). Using the Pythagorean Theorem, the length of AC is equal to 126.6.
To calculate this, we take the square root of (b² + 99.6²). First, we square b, which is 85. This gives us 7225. Then, we square 99.6, which gives us 9920.41. We then add these two values together to get 17145.41. Finally, we take the square root of this value, which gives us 126.6. This is the length of AC in the given triangle.
Learn more about Pythagorean Theorem here:
https://brainly.com/question/14930619
#SPJ1
express 2/(1-(x^2)) into partial fractions
Answers
2/ ( 1 + x) ( 1 - x) is express into partial fractions.
With an example, what is a partial fraction?
The division of an algebraic fraction into smaller, "partial fractions," components is possible. Think about the algebraic fraction (3x+5) (2x2-5x-3). This formula can be broken down into its simplest form, [2/(x - 3)] - [1/(2x + 1)]. Partial fractions are the more straightforward pieces [2/(x - 3)] and [1/(2x + 1)].
The four categories of partial fractions are linear factors, degree 2 irreducible factors, repeated linear factors, and repeated irreducible degree 2 factors.
= 2/(1-(x^2))
= 2 / (1)² - (X)²
= 2/ ( 1 + x) ( 1 - x)
Learn more about partial fraction
brainly.com/question/29177355
#SPJ1
Some parts of California are particularly earthquake-prone. Suppose that in one metropolitan area, of all homeowners are insured against earthquake damage. Four homeowners are to be selected at random; let denote the number among the four who have earthquake insurance.
1. Find the probability distribution of X. [Hint: Let S denote a homeowner who has insurance and one who does not. Then one possible outcome is SFSS, with probability (.25)(.75)(.25)(.25) and associated X value 3. There are 15 other outcomes].
2. What is the most likely value for X?
3. What is the probability that at least two of the four selected have earthquake insurance?
Answers
Missing part of the question
Some parts of California are particularly earthquake-prone. Suppose that in one metropolitan area, 25% of all homeowners.....................
Answer:
\(P(X = x) = ^4C_x * 0.25^x * 0.75^{4-x}\)
\(Mean = 1\)
\(Pr = 0.2617\)
Step-by-step explanation:
Given
\(n = 4\)
\(p = 25\%\)
Solving (a): The probability distribution of x
We have:
\(n = 4\)
\(p = 25\%\) \(= 0.25\)
The probability of not having earthquake insurance (q) is:
\(q = 1 - p\)
\(q = 1 - 0.25\) \(= 0.75\)
If x has insurance, then n - x do not.
The distribution follows a binomial pattern. So, the probability distribution is:
\(P(X = x) = ^nC_x * 0.25^x * 0.75^{n-x}\)
Substitute 4 for n
\(P(X = x) = ^4C_x * 0.25^x * 0.75^{4-x}\)
Solving (b): The most likely value of x i.e. The mean
We have:
\(n = 4\) and
\(p = 25\%\) \(= 0.25\)
\(Mean = np\)
\(Mean = 4 * 0.25\)
\(Mean = 1\)
Solving (c): At least 2 of 4 selected have earthquake insurance.
This is calculated as
\(Pr = P(x = 2) + P(x = 3) + P(x = 4)\)
\(P(X = x) = ^4C_x * 0.25^x * 0.75^{4-x}\)
\(P(X=2) = ^4C_2 * 0.25^2 * 0.75^{4-2}\)
\(P(X=2) = 6 * 0.25^2 * 0.75^2 = 0.2109375\)
\(P(X=3) = ^4C_3 * 0.25^3 * 0.75^{4-3}\)
\(P(X=3) = 4 * 0.25^3 * 0.75 = 0.046875\)
\(P(X=4) = ^4C_4 * 0.25^4 * 0.75^{4-4}\)
\(P(X=4) = 1 * 0.25^4 * 1= 0.00390625\)
So:
\(Pr = P(x = 2) + P(x = 3) + P(x = 4)\)
\(Pr = 0.2109375 + 0.046875 + 0.00390625\)
\(Pr = 0.26171875\)
\(Pr = 0.2617\) --- approximated
Suppose that four men and four women will be randomly lined up, from left to right, with all possible orderings of these eight people being equally likely. What is the probability that the men will be in alphabetical order, from left to right, and at the same time the women will also be in alphabetical order, from left to right
Answers
Answer:
P = 1 / 40320 or P = 2.48*10⁻⁵
Step-by-step explanation:
The total number of outcomes To is:
To = 8! To = 8*7*6*5*4*3*2
To = 40320
Of all these outcomes there is only one proper outcome, therefore the probability of having all men and women in alphabetical order is:
P = 1 / 40320 or P = 2.48*10⁻⁵
What does the expression ∙ represent?
Answers
If you mean the • dot, it means multiplication.
Answer:
The expression l*w means length times Width, which you will learn in Geometry