Answers
The value of x in the quadratic equation is 2 or 2
What is quadratic equation?A quadratic equation is a second-order polynomial equation in a single variable x ax²+bx+c=0. with a ≠ 0 .
There are different methods of solving a quadratic equation but in this case we are using the formula method.
x = -b±√b² -4ac)/2a
for the equation x²-4x +4 = 0
a = 1, b = -4 and c = 4
-(-4) ±√ -4² -4×1 × 4)/2
x = 4 ± √ 16-16)/2
x = 4 ± √0)/2
x = 4 /2 or 4/2
x = 2 or 2
Therefore the value of x is 2 or 2
learn more about quadratic equation from
https://brainly.com/question/28038123
#SPJ1
Related Questions
StartFraction negative 8 (17 minus 12) over Negative 2 (8 minus (negative 2)) EndFraction
Answers
-2(8-(-2)) = -2(10) = -20
-40/-20 = 2
Answer : 2
Answer:
2
Step-by-step explanation:
i took the test
Identify the following dilemmas as either constructive or destructive. Then suggest a refutation for each by escaping between the horns, grasping by the horns, or constructing a counterdilemma.
If the Mitchells get a divorce, they will live separately in poverty; but if they stay married, they will live together in misery. Since they must either get a divorce or stay married, they will either live separately in poverty or together in misery.
Answers
This is a false dilemma, also known as a black-and-white fallacy, which presents only two extreme options and assumes that there are no other alternatives.
In this case, the dilemma suggests that the only two choices for the Mitchells are to get a divorce or to stay married, and both options have negative outcomes. However, there may be other alternatives that are not considered in this dilemma, such as counseling, financial planning, or other ways to improve their relationship and financial situation.
A possible refutation could be constructing a counterdilemma, such as:
Are there no other alternatives for the Mitchells to consider besides getting a divorce or staying married? What if they sought professional counseling or financial advice to address their issues?
Are poverty and misery the only possible outcomes for the Mitchells if they get a divorce or stay married? What if they found ways to improve their financial situation or relationship while living apart or together?
By questioning the premise of the dilemma and considering other options, we can escape between the horns or grasp the situation by the horns and find a better solution.
To know more about the Dilemmas visit:
https://brainly.com/question/16313637
#SPJ4
Write the first expression in terms of the second if the terminal point determined by t is in the given quadrant. cos(t), sin(t); quadrant iv
Answers
if the terminal point indicated by t is in the provided quadrant, the first equation in terms of the second quadrant iv; cos(t), sin(t). \(\sin t=\sqrt{1-\frac{1}{\sec ^2 t}}\)
What is Trig Identities?Trig identities come in handy when we need to express one trig function in terms of another. The most famous trig identity is derived straight from the Pythagorean Theorem:
sin² t + cos² t = 1
According to the given data:For an angle t in Quadrant IV, we know sin t is positive.
From the trig identity sin² t + cos² t = 1
we can also write as:
sin t + cos t:
Now,
sin² t + cos² t = 1
sin² t = 1 - cos² t
sin t = ±√( 1 - cos² t)
As noted above,
sin t is positive for t in the Quadrant IV, and so we have
sin t = √( 1 - cos² t)
We know that
\(\cos t=\frac{1}{\sec t}\)
So, the equation will be
\(\sin t=\sqrt{1-\frac{1}{\sec ^2 t}}\)
To know more about Trig Identities visit:
https://brainly.com/question/10376944
#SPJ4
practice multiplying monomials and binomials. what is the product of 3x(x2 4)? x2 3x 4 3x3 4 3x3 12x 3x2 12x
Answers
Therefore the solution of the given problem is product of the equation is 3\(x^{3}\) + 12x.
Define equation.The equals sign (=) must appear in an equation. You can think of an equation as having a left and a right side since there will be a mathematical expression on either side of it. Consider an equation to be a set of scales. Although you can use different amounts on either side, for it to be solved, each side must be equally balanced .An unknown will always be present in an algebraic equation. This is symbolized by a symbol, such x, y, or z.
Here,
We must calculate the product of 3x(\(x^{2}\) + 4).
In light of the query
Follow all of the instructions listed below to obtain the equation's product.
Equation; 3x(\(x^{2}\) + 4).
Then,
The product of the equation is,
=>3x(\(x^{2}\) + 4).
=>3\(x^{3}\) + 12x
Therefore the solution of the given problem is product of the equation is 3\(x^{3}\) + 12x.
To know more about equation , visit
https://brainly.com/question/10413253
#SPJ4
Which of the following represents a sum from the expression given?
A. 21
B. 2
C. 13x2
D. 13x2 + 8x
Answers
Please help me with this question!!

Answers
Answer:
the answer you are looking for is B
Answer:
i think the answer is A
Step-by-step explanation:
what is the domain of validity for csc 0=1/sin 0
a. all real numbers
b. all real numbers except odd multiples of pi/2
c. all real numbers except even multiples of pi/2
d. all real numbers except multiples of pi
Answers
The correct answer is (b) all real numbers except odd multiples of π/2. The domain of validity for cscθ (cosecant) is restricted because cosecant is undefined when the sine of an angle is zero.
In the trigonometric identity cscθ = 1/sinθ, the denominator sinθ becomes zero at odd multiples of π/2 (such as π/2, 3π/2, 5π/2, etc.), resulting in a division by zero error. Therefore, the cosecant function is not defined for these values of θ.
For all other real numbers θ, the sine function is non-zero and well-defined, allowing us to calculate the reciprocal of the sine and determine the value of the cosecant. Hence, the domain of validity for cscθ is all real numbers except odd multiples of π/2, as stated in option (b).
It's important to note that in trigonometry, the domain of validity is determined by avoiding any values that would lead to undefined expressions or division by zero errors.
Learn more about trigonometric identity here:
https://brainly.com/question/12537661
#SPJ11
The domain of validity for csc θ = 1/sin θ is all real numbers except multiples of π, because at these points the sine function equals zero, and division by zero is undefined.
Explanation:In mathematics, the cosecant function (csc), is defined as the reciprocal of the sine function, or 1/sinθ. The domain of a function are all the possible input values that will yield real numbers (output). For the csc function, its domain includes all real numbers except where the denominator is zero because division by zero is undefined.
In the unit circle context, sine equals zero at 0, π, 2π, ..., and the negative counterparts. Basically, these are the multiples of π. Thus, for the csc function, the domain is all real numbers except multiples of π, which matches option d in your choices.
The domain of validity for csc θ = 1/sin θ is all real numbers except multiples of π.
Learn more about Domain of cosecant function here:https://brainly.com/question/34222210
#SPJ12
Plsssssssssssss help

Answers
Answer:
C
Step-by-step explanation:
The graph is showing a slope of 3/2. The only option showing this slop is c.
Use limits to determine if
x+3
f(x) = is continuous at x = 3.

Answers
The correct answer is (d) No, it is not continuous because lim x→3 f(x) ≠ lim x→3 f(x).
To determine if the function f(x) = (x+3)/(x²-9) is continuous at x=3, we need to check if the limit of the function exists as x approaches 3 from both the left and the right, and whether this limit is equal to the value of the function at x=3.
First, we can check the limit as x approaches 3 from the left:
lim x→3- f(x) = lim x→3- (x+3)/(x²-9) = (-3)/(0-) = ∞
Next, we can check the limit as x approaches 3 from the right:
lim x→3+ f(x) = lim x→3+ (x+3)/(x²-9) = (6)/(0+) = ∞
Since both one-sided limits are infinite, the limit as x approaches 3 does not exist.
Therefore, the function f(x) = (x+3)/(x²-9) is not continuous at x=3.
The correct answer is (d) No, it is not continuous because lim x→3 f(x) ≠ lim x→3 f(x).
To know more about continuity visit:
brainly.com/question/21447009
#SPJ1
Using the arithmetic growth approximation of population increase, estimate the population of Frankfort, KY after 20 years of (arithmetic) growth. In 2020, the population of the Frankfort was 28,602. In 2010, the population of Frankfort was 25,527. Estimate the population in 2040. Chegg
Answers
The estimated population of Frankfort, KY in 2040 using the arithmetic growth approximation is approximately 34,752.
To estimate the population of Frankfort, KY after 20 years of arithmetic growth, we need to calculate the average annual growth rate first. We can use the formula:
Average Annual Growth Rate = (Ending Population - Starting Population) / (Number of Years)
Using the provided population data, we can calculate the average annual growth rate:
Average Annual Growth Rate = (28,602 - 25,527) / (2020 - 2010)
= 3,075 / 10
= 307.5
Now, we can use the arithmetic growth approximation formula to estimate the population in 2040:
Estimated Population in 2040 = Starting Population + (Average Annual Growth Rate ×Number of Years)
Estimated Population in 2040 = 28,602 + (307.5 × 20)
= 28,602 + 6,150
= 34,752
Therefore, the estimated population of Frankfort, KY in 2040 using the arithmetic growth approximation is approximately 34,752.
Learn more about arithmetic growth here:
https://brainly.com/question/31870974
#SPJ11
HELP WHAT IS 45782 DIVIDED BY 30!!!!!!!!!!!
Answers
Answer:
1526.1
Step-by-step explanation:
45782 DIVIDED BY 30 is 1526.1
Answer:
152 Remainder 18
Step-by-step explanation:
thank the air and cardboard boxes have a great day.
tommie the turtle is receiving threats, so ranger dave builds the advanced rectangular storage container (a box with an open top) to store these threats. at. the a.r.c. is to have a volume of 10 m^3 , and the length of the base is to be twice its width. b. material for the base costs $10 per square meter. c. material for the sides costs $6 per square meter. d. find the dimensions for the least-expensive c.a.r.s. that can be built to those specifications.
Answers
The least expensive C.A.R.S. that can be built to those specifications has dimensions of approximately 4.3088 m x 2.1544 m x 1.7321 m and will cost about $265.47 to build.
Let's start by looking at the dimensions of the base. We know that the length of the base is twice its width. Let's represent the width of the base as "x." This means that the length of the base is "2x." The area of the base is simply the product of the length and the width, which is 2x * x = 2x².
Next, let's look at the dimensions of the sides. The height of the box is going to be represented by "h." The length of each side is going to be equal to the length of the base, which we already know is 2x. The width of each side is going to be equal to the width of the base, which is just x. So the area of each side is simply 2hx.
Now we can use the formula for the volume of a rectangular prism to find the value of "h" in terms of "x." The volume of the box is given as 10 m^3, so:
V = lwh = (2x)(x)(h) = 10
Simplifying this equation, we get:
2x²h = 10
Solving for "h," we get:
h = 5/x²
Now that we have an expression for "h" in terms of "x," we can use it to find the total surface area of the box, which is the sum of the area of the base and the area of the four sides. We can then use this expression to find the minimum cost for a given volume of the box.
The total surface area of the box is given by:
A = 2x² + 4(2hx)
Substituting the expression we found for "h" into this equation, we get:
A = 2x² + 4(2x)(5/x²)
Simplifying this equation, we get:
A = 2x² + 40/x
Now we can take the derivative of this expression with respect to "x" and set it equal to zero to find the value of "x" that will minimize the cost of the box. Differentiating and setting equal to zero, we get:
dA/dx = 4x - 40/x² = 0
Solving for "x," we get:
x^3 = 10
Taking the cube root of both sides, we get:
x ≈ 2.1544
Now we can use this value of "x" to find the dimensions of the least expensive C.A.R.S. that can be built to those specifications. The length of the base is twice the width, so:
Length = 2x ≈ 4.3088
Width = x ≈ 2.1544
Height = 5/x² ≈ 1.7321
So the dimensions of the least expensive C.A.R.S. that can be built to those specifications are approximately: Length = 4.3088 m Width = 2.1544 m Height = 1.7321 m
These dimensions will allow us to build a C.A.R.S. with a volume of 10 m^3, while using the least amount of material possible, which means that the cost will be minimized. We can verify this by calculating the total surface area of the box and the cost of the materials needed.
The total surface area of the box can be calculated by substituting the values we found for "x" and "h" into the expression we derived earlier:
A = 2(2.1544)² + 4(2)(5)/(2.1544)² ≈ 28.2742 m²
Now we can calculate the cost of the materials needed to build the box:
Cost = (Area of base)(Cost per square meter for base) + (Area of sides)(Cost per square meter for sides)
Cost = (2.1544²)(10) + (28.2742 - 2(2.1544²))(6) ≈ $265.47
To know more about dimensions here
https://brainly.com/question/28688567
#SPJ4
1 over 5 +2 over 25 =
Answers
Answer:
33
Step-by-step explanation:
Addition
Answer:
0.28
(1 / 5) + (2 / 25) = 0.28
What’s the value of x
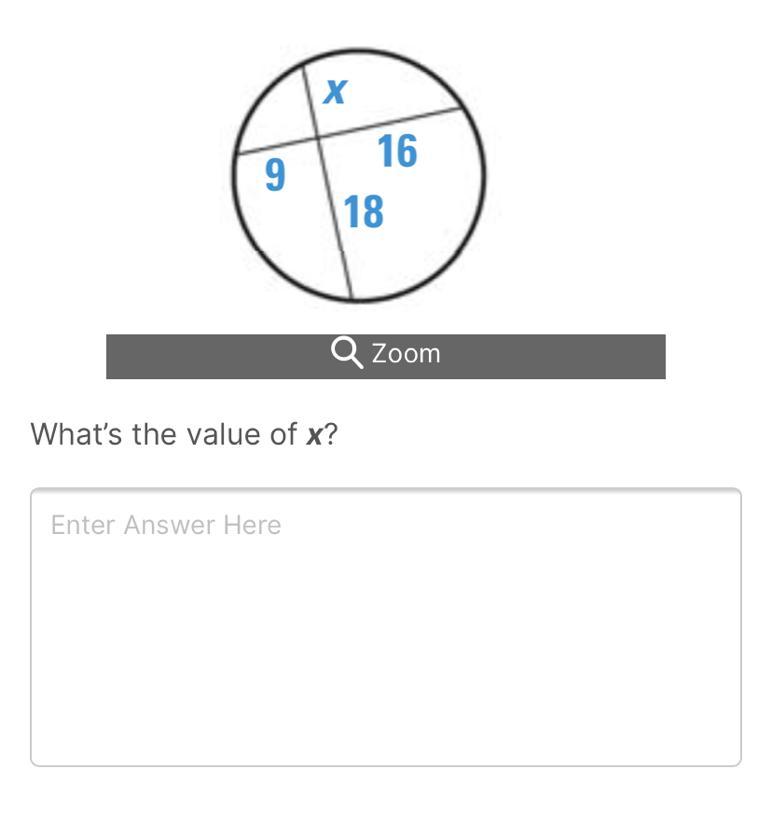
Answers
X=9.
What is ( x3 )4 in expanded form?
Answers
Answer:
Step-by-step explanation:
here you go mate
step 1
(x^3)4 equation
step 2
(x^3)4 simplify
answer
4x^3
can i get brainliest if you dont mind
What is the rate of change of the linear function that has a graph that passes through the points (-3, 7) and (5, -9)?
Answers
The rate of change of that linear function is.
\(m=\frac{-9-7}{5-(-3)}\)\(m=\frac{-16}{8}=-2\)Sophia trains with her friend Asha on a
Asha starts running right after school and runs an average of one kilometer in seven minutes
Sophia leaves 10 minutes later and runs at a steady pace shown in the table below:
Write each function as a linear equation where x is the number of kilometers and y is the number of minutes
who runsaster? Explain
1
2
3
5
10
15.5
25.5
37.5

Answers
Answer:
Simplify 2 pears , any pears 2 on the top and 2 on the bottom and you will get your answer . You got this
Step-by-step explanation:
Let n be a positive integer and a power of 2 i.e. n=2i where i=0,1,2⋯. Consider a function T(n) such that T(1)=1 and, for n>1, T(n)≤3n2+2n+7+T(2n). Prove that T(n)=O(n3)
Answers
If we choose c = 20, we have T(n) ≤ 20 * \(n^3\) for all n ≥ n0, Thus, we have proven that T(n) = \(O(n^3)\) as desired.
Let's use mathematical induction to prove this statement.
Base case:
For n = 1, T(1) = 1 which is less than or equal to \(c * 1^3\) for any positive constant c. Therefore, the base case holds true.
Inductive hypothesis:
Assume that T(k) ≤ c * k^3 for all positive integers k where k < n.
Inductive step:
We need to prove that T(n) ≤ \(c * n^3.\)
From the given function T(n) = \(T(2n) + 3n^2 + 2n + 7\), we can rewrite it as \(T(n) - T(2n) ≤ 3n^2 + 2n + 7.\)
By the inductive hypothesis, we have \(T(2n) ≤ c * (2n)^3 = 8c * n^3.\)
Substituting this into the previous inequality, we get \(T(n) - 8c * n^3 ≤ 3n^2 + 2n + 7.\)
Rearranging the terms, we have \(T(n) ≤ 8c * n^3 + 3n^2 + 2n + 7.\)
Now, we need to find a value of c and n0 such that \(8c * n^3 + 3n^2 + 2n + 7 ≤ c * n^3 for all n ≥ n0.\)
Since the highest power of n in the expression on the left side is n\(^3\), we can choose c ≥ 8 + 3 + 2 + 7 = 20.
Therefore, if we choose c = 20, we have T(n) ≤ 20 * n^3 for all n ≥ n0,
Thus, we have proven that T(n) = O\((n^3)\) as desired.
To know more about hypothesis visit:
https://brainly.com/question/32298676
#SPJ11
Why is it important to center the x value before squaring? Because X-squared is strongly correlated with Because squaring the x values without centering them first reduces the effects of multicollinearity Because the residual plot needs to have a distinct pattern Because centering the x values will straighten the curve of the scatterplot
Answers
Centering x values before squaring eliminates the correlation between x and its square term, reducing multicollinearity. This helps to determine independent effects of predictor variables, and can also straighten the curve of a scatterplot.
Centering the x values before squaring is important because it helps to eliminate the correlation between the x variable and its square term. When we square a variable without centering it, we are essentially capturing the effect of both the linear and the quadratic terms.
This can lead to multicollinearity, which occurs when two or more predictor variables are highly correlated with each other.
Multicollinearity can create problems in statistical analyses because it can make it difficult to determine the independent effects of each predictor variable on the outcome variable. Centering the x values before squaring helps to reduce the effects of multicollinearity by eliminating the correlation between the x variable and its square term.
To know more about multicollinearity:
https://brainly.com/question/29737655
#SPJ4
Reggie has $350 he received for his birthday. Every month, $25 is removed from his account to go to his college savings (no other transactions are made). Create and solve an equation that can be used to find the number of months, m, it takes for the account balance to reach $225.
I need an equation ASAP!
Answers
Answer:
reggie is stuopid he should spend it on bubgle gum.
Step-by-step explanation:
Answer:
225=-25x+350 (x=5 months)
Step-by-step explanation:
Archer receives a day's work of pay, p, for 5 days of mowing lawns. He spent half of his money on gas. Then he spent $5 on water. Now, he has $40 left. Which equation represents how much Archer would get paid each day of mowing lawns?
Answers
Answer:
Daily pay= $18
5 days pay = $90
Step-by-step explanation:
Archer's daily pay =p
Pay for 5 days= 5p
Gas = 1/2 of 5p
= 1/2 × 5p
= 5p/2
Water = $5
Balance = $40
5p = 5/2p + 5 + 40
5p - 5/2p = 45
10p -5p /2 = 45
5/2p = 45
p= 45÷ 5/2
= 45 × 2/5
= 90/5
P= $18
5p= 5 × $18
=$90
The equation to determine Archer's daily pay is
5p = 5/2p + 5 + 40
Divide both sides by 5
p = 5/2p + 45 ÷ 5
= (5/2p + 45) / 5
p= (5/2p + 45) / 5
PLEASE HELP ASAP
18. A surveyor intends to create a bridge across a river. There is a tall tree on the other side of the river. He
measures a line down his side of the river for 125 feet. At each side of this line he uses his surveying
equipment to measure the angle to the tree on the other side of the river. At the beginning of the line, the
angle to the tree was 65°10', at the end of the line the angle to the tree is 60°10'. If he wants the bridge to go
from where he started his line to the tree, then how long will the bridge be?
Answers
The 125 feet long line and the angles 65°10', and 60°10' obtained from the surveying equipment gives the length of the bridge as approximately 1234.2 feet.
Which rule can be used to find the length of the bridge?Given;
Location of the tree = The other side of the river from the surveyor
Length of the line measured along the river, L = 125 feet
Angle to the tree from the start of the line = 65°10'
1° = 60'
10' = ((1/60)×10)° = (1/6)°
65°10' = (65 + 10/60)° = (65 + 1/6)°
Angle measured at the end of the line, E = 60°10'
Similarly;
E = 60°10' = (60 + 1/6)°
The interior angle, S, of the triangle formed by the tree and the line, at the start of the line is therefore;
Angle S = 180° - (65 + 1/6)° = (114+5/6)° (linear pair angles)
S = (114+5/6)°
From the angle sum property of a triangle, angle formed at the tree, T, is therefore;
T = 180° - ((114+5/6)° + (60 + 1/6)°) = 5°
According to the rule of sines, we have;
l/(sin T) = b/(sin E)
Where;
b = The length of the bridge
Which gives;
124/(sin 5°) = b/(sin (60 + 1/6)°)
b = (sin (60 + 1/6)°) × (124/(sin 5°)) ≈ 1234.2
The length of the bridge, b ≈ 1234.2 feetLearn more about the rule of sines here:
https://brainly.com/question/4372174
#SPJ1
12. Two very long parallel wires perpendicular to the xy plane and d = 8m eport. They carry identical currents - 90 A out of the page (*2 direction) The magnitude of the magnetic field generated by these wires at the point (* = 4 m. y 4 m) is a) 1.50x10T b) 2.50x10"T IT T c) 3.50x10'T ALATT
Answers
The magnetic field generated by the wires at the point (x=4m, y=4m) carrying identical currents of 90A out of the page is 2.50 x \(10^{-6\) T or 2.50 μT.
Hence option b is correct.
According to the given information,
We can use the Biot-Savart Law to calculate the magnetic field generated by these wires at the given point.
Using the formula, we get:
B = (μ0/4π) I [(sinθ1 + sinθ2) / 2] / d,
Where,
μ0 is the permeability of free space (4π x \(10^{-7}\) T m/A),
I is the current (90 A),
θ1 and θ2 are the angles between the wire and the vector pointing from the wire to the given point,
And d is the distance between the wires (8 m).
To find θ1 and θ2, we can use Trigonometry:
θ1 = sin inverse (y/d)
= sin inverse (4/8) = 30°
θ2 = sin inverse [(y-d)/d]
= sin inverse [(4-8)/8]
= -30°
Substituting these values into the formula, we get:
B = (4π x \(10^{-7}\) T m/A) 90 A [(sin30° + sin(-30°)) / 2] / 8 m
B = 2.50 x \(10^{-6\) T
= 2.50 μT
Therefore, the correct option is (b) 2.50 x \(10^{-6\) T (or 2.50 μT).
To learn more about magnetic fields visit:
https://brainly.com/question/14848188
#SPJ4
The complete question is attached below:

Tessa and Kari are swimming partners in series of practice swims they each swim longer and longer distances without changing pace they each set up a table to show the ratios of distance to time for their swims.
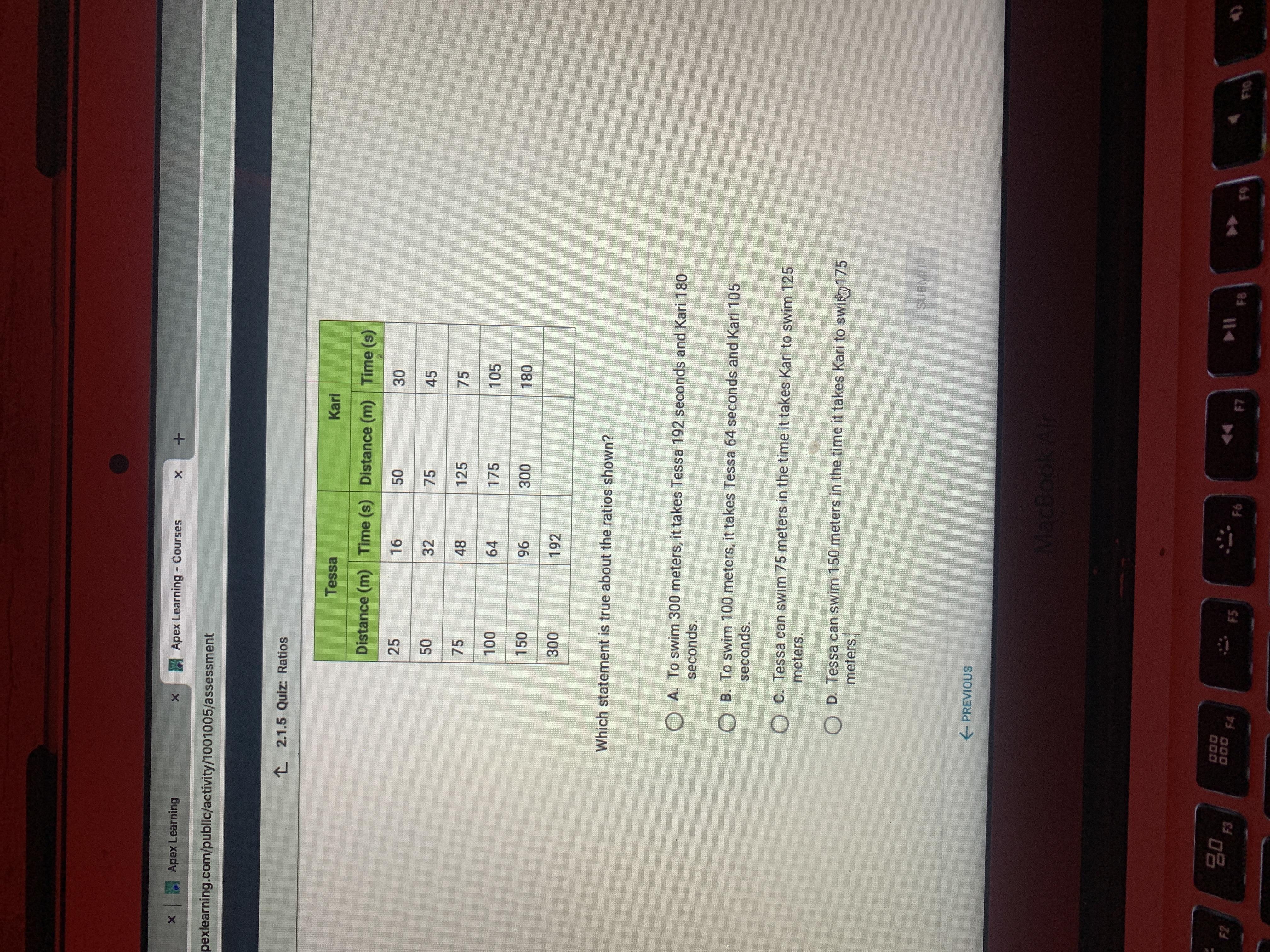
Answers
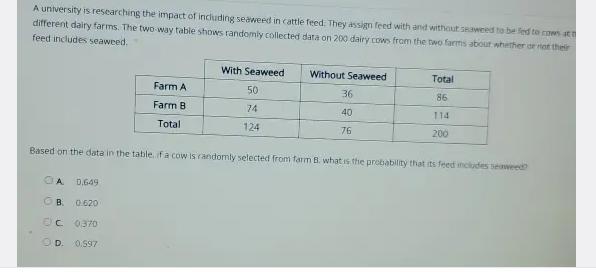
A university is researching the impact of including seaweed in cattle feed. They assign feed with and without seaweed to be fed to cows at two different dairy farms.
Answers
If a cow is randomly selected from farm, the probability that its feed includes seaweed is option A. 0.649.
What is the probability?To be able to find the probability that a randomly selected cow from Farm B has feed that is seen in the seaweed, one have to calculate the ratio of the number of cows on Farm B with seaweed feed to that of the total number of cows on Farm B.
Note that based on table given, the number of cows on Farm B with seaweed feed = 74 while total number of cows on Farm B = 114.
So , the probability that its feed includes seaweed is :
Probability = Number of cows with seaweed feed on Farm B / Total number of cows on Farm B
= 74 ÷ 114
≈ 0.649
Therefore, the probability that its feed includes seaweed is option A. 0.649.
Learn more about probability from
https://brainly.com/question/24756209
#SPJ1
See full text below
A university is researching the impact of including seaweed in cattle feed. They assign feed with and without seaweed to be fed to cows at t different dairy farms. The two-way table shows randomly collected data on 200 dairy cows from the two farms about whether or not their feed includes seaweed.
With Seaweed Without Seaweed Total
Farm A 50 36 86
Farm B 74 40 114
Total 124 76 200
Based on the data in the table, if a cow is randomly selected from farm B. what is the probability that its feed includes seaweed?
A. 0.649
B. 0.620
C 0.370
D. 0.597
the equivalent metric length of a 3-inch scar would be
Answers
Therefore, the equivalent metric length of a 3-inch scar would be 7.62 centimeters.
Explanation: Metric length is a measurement system that uses the metric unit. The metric unit is more common than the customary unit system in the United States. To convert customary unit lengths to metric lengths, a conversion factor is used.3 inches is the measurement of the scar in customary units. To convert 3 inches to metric units, multiply it by the conversion factor. There are 2.54 centimeters in one inch, which is the conversion factor. To find the equivalent metric length of a 3-inch scar, multiply 3 by 2.54. Therefore, the equivalent metric length of a 3-inch scar would be 7.62 centimeters. The equivalent metric length of a 3-inch scar would be 7.62 centimeters. Metric length is a measurement system that uses the metric unit. The metric unit is more common than the customary unit system in the United States. To convert customary unit lengths to metric lengths, a conversion factor is used. There are 2.54 centimeters in one inch, which is the conversion factor.
Therefore, the equivalent metric length of a 3-inch scar would be 7.62 centimeters.
To learn more about scale factor visit:
https://brainly.com/question/29967135
#SPJ11
Given
h
(
x
)
=
−
x
−
1
h(x)=−x−1, find
h
(
−
2
)
h(−2).
Answers
Answer:
h(-2) = 1
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Functions
Function NotationStep-by-step explanation:
Step 1: Define
Identify.
h(x) = -x - 1
Step 2: Evaluate
Substitute in x [Function h(x)]: h(-2) = -(-2) - 1Simplify: h(-2) = 2 - 1[Order of Operations] Subtract: h(-2) = 1please help i mark brainiliest

Answers
Answer:
2: 15
3: 20
for the second chart
0: -2
2: 8
4: 18
6: 28
I hope this helped :))
i hope this is correct '~'
In Spanish class, Kevin learns an average of 34.5 new words per months. If he takes Spanish for 9 months, which is the best estimate for about how many words he will learn?
A. 350 words
B. 355 words
C. 360 words
D. 365 words
(ESTIMATE)
PLEASE HELP I KEEP GETTING 306 AND I DON’T GET IT
Answers
The number of words he will learn is estimated at (a) 350 words
How to determine the number of words he will learn?From the question, we have the following parameters that can be used in our computation:
Words per month = 34.5 new words
Number of months = 9 months
The estimate of the number of words he will learn is calculated using the following equation
Number of words = Words per month * Number of months
Substitute the known values in the above equation, so, we have the following representation
Number of words = 34.5 * 9
When the values are estimated, we have
Number of words = 35 * 10
Evaluate the products
Number of words = 350
Hence, the estimate is (a) 350 words
Read more about estimates at
https://brainly.com/question/16037112
#SPJ1
The perimeter of a park is 10 km . A wall is being constructed around it . If 4/5 of the wall has been constructed , how much part of the wall is incomplete
Answers
Perimeter of the park = 10km
Part of the wall's construction completed =
\( \frac{4}{5}th \: of \: perimeter \)
=
\( \frac{4}{5} \times 10\)
(cancel 5 and 10)
=
\( \frac{4}{1} \times 2\)
= 8km
•.• Part of the wall left (to be constructed) = 10km - 8km = 2km
HOPE THIS HELPS YOU
