Answers
188 is the answer of questions
Related Questions
please help don,t undertan
Answers
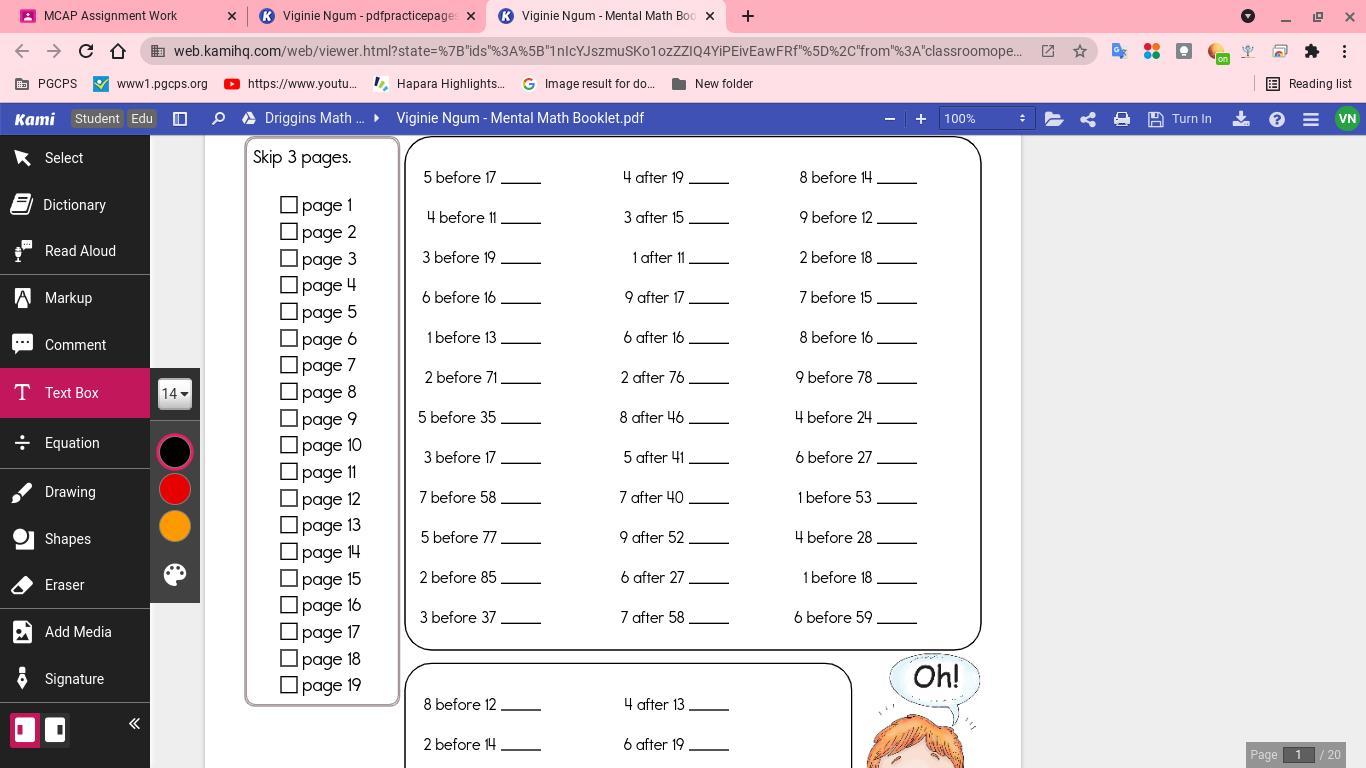
Answer:
substract.
Step-by-step explanation:
eg. 5 before 17 = 17-5
so 5 before 17= 12
same for others
Graph the following inequality. x> -4
Answers

I need help with this question

Answers
The domain and range of the given function are [−3,∞) and [0,∞) respectively.
The given function is f(x)=2√(x+3).
Find the domain by finding where the function is defined. The range is the set of values that correspond with the domain.
The domain and range are defined for a relation and they are the sets of all the x-coordinates and all the y-coordinates of ordered pairs respectively.
Domain: [−3,∞),{x|x≥−3}
Range: [0,∞),{y|y≥0}
Therefore, the domain and range of the given function are [−3,∞) and [0,∞) respectively.
To learn more about the domain and range visit:
brainly.com/question/28135761.
#SPJ1
I need help! ASAP!! please and thank you

Answers
Answer: The walking path around it.
Step-by-step explanation:
Remember the Pythagorean's theorem, for a triangle rectangle with catheti A and B, and with hypotenuse H, we have:
A^2 + B^2 = H^2
or
H = √(A^2 + B^2)
Here, A + B is the total distance for the path, while the hypotenuse is the distance for the bridge
Here we can see that:
A = 1170 ft
B = 520 ft
Then:
H = √( (520 ft)^2 + (1170 ft)^2) = 1280.4 ft
Now, let's compute the costs.
For the bridge, we know that each foot costs $11, then for 1280.4 ft the cost is:
Cost of the bridge = (1280.4)*$11 = $14,084.4
And for the walking path, the cost is $6 per foot, then the total cost of the path is:
Cost of the path = (520 ft + 1170 ft)*$6 = $10,140
We know that the bridge is preferred if it is within the range of $1500 for the path's cost.
This range is:
($10,140 - $1,500, $10,140 + $1,500) = ($8,640, $11,640)
Here we can see that the cost of the bridge does not belong to this range, (is higher) so the option we should recommend is the walking path around.
HELPPP PYTHAGOREAN THEOREM

Answers
Answer:
60
Step-by-step explanation:
We can use the Pythagorean theorem since this is a right triangle
a^2+b^2 = c^2 where a and b are the legs and c is the hypotenuse
a^2+25^2 = 65^2
a^2 +625 = 4225
a^2 = 4225-625
a^2=3600
Taking the square root of each side
sqrt(a^2) = sqrt(3600)
a = 60
Answer:
Step-by-step explanation:
Hypotenuse: 65
Leg: 25
Let Hypotenuse be c, and leg be a
\(a^{2}\) + \(b^{2} = c^{2}\)
\(a^{2} + 25^{2} = 65^{2}\)
\(a^{2} + 625 = 4225\\\)
\(a^{2}\) = 4225 - 625
\(a^{2}\) = 3600
3600 is the exponential value of a, meaning we need to apply the opposite of squaring to get the value of b. Which is square rooting.
a = \(\sqrt{3600\\}\)
a = 60
Therefore a is equal to 60 feet
ASAP PLEASE HELP IF RIGHT ANSWER WILL GIVE BRAINLIEST, 15 POINTS, AND 5 STAR OVERALL!!!! IF WRONG ANSWER OR INVALID WILL REPORT, PLEASE, PLEASE, PLEASE!!

Answers
Answer:
Hope this helps with your question :)
B
Step-by-step explanation:
This is because in the slope-intercept form,
y = mx + b, the m = slope, and the b = y-intercept. So the final answer would be
y = 1/2x - 5
80 POINTS! Help with this question please!!!! 80 POINTS!

Answers
Answer:
C. Translation 5 units left and 2 units down
Step-by-step explanation:
Let's take a look at A', which is (0, 0). This is the result of A, which is (5, 2) being transformed somehow. Notice that the x-coordinate moved 5 units to the left (from 5 to 0, which means we subtract 5 from 5). And, notice that the y-coordinate moved 2 units down (from 2 to 0, so we subtract 2 from 2).
Look to see if this works for the other two points:
B(6, 1): if we subtract 5 from the x-coordinate 6, we get 6 - 5 = 1, which matches the x-coordinate of the image B'. If we subtract 2 from the y-coordinate of B, which is 1, we get 1 - 2 = -1, which also matches the y-coordinate of B'. So, this works.
C(4, 5): if we subtract 5 from the x-coordinate 4, we get 4 - 5 = -1, which matches the x-coordinate of the image C'. If we subtract 2 from the y-coordinate of C, which is 5, we get 5 - 2 = 3, which also matches the y-coordinate of C'. So, this again works.
Therefore, we know that the transformation is a translation 5 units left and 2 units down, or C.
A picture will be shown below of a graph with the points in the table.
We only need to use (5, 2) and (0, 0) to solve this problem.
We take both points and see what it took for the old point to get to where the new point is (Shown in picture below).
Therefore, the answer is [ C. Translation 5 units left and 2 units down ]
Best of Luck!

a set of x and y scores has b = 4, mx = 12, and my = 51. what is the y-intercept (a) for the regression equation?
Answers
The y-intercept for the regression equation is 3, given that b = 4, Mx = 12, and My = 51. So, the correct option is C).
The formula for the y-intercept of the regression equation is
a = My - b(Mx)
where My is the mean of the dependent variable (y), b is the slope, and Mx is the mean of the independent variable (x).
Given that b = 4, Mx = 12, and My = 51, we can substitute these values in the formula to find the y-intercept
a = 51 - 4(12)
a = 51 - 48
a = 3
Therefore, the y-intercept (a) for the regression equation is 3.
The correct Answer is C) 3.
To know more about regression equation:
https://brainly.com/question/30738733
#SPJ4
--The given question is incomplete, the complete question is given
" A set of X and Y scores has b = 4, Mx = 12, and My = 51. What is the y-intercept (a) for the regression equation? O 9.75 17.36 3.00 8.25 "--
Question 2 Let a complex number Z be 4 + j6.22. Without using a graphics calculator (scientific is okay), what is loge (Z)?
Answers
A complex number Z be 4 + j6.22. The logarithmic formula:
loge(Z) ≈ ln(7.39) + j * 1.005
To calculate the natural logarithm of a complex number, we can use the logarithmic properties of complex numbers. The logarithm of a complex number Z is defined as:
loge(Z) = ln(|Z|) + j * arg(Z)
where |Z| is the magnitude (or absolute value) of Z, and arg(Z) is the argument (or angle) of Z.
Given Z = 4 + j6.22, we can calculate the magnitude and argument as follows:
|Z| = √(Re(Z)² + Im(Z)²)
= √(4² + 6.22²)
= √(16 + 38.6484)
= √(54.6484)
≈ 7.39
arg(Z) = arctan(Im(Z) / Re(Z))
= arctan(6.22 / 4)
≈ 1.005
Now we can substitute these values into the logarithmic formula:
loge(Z) ≈ ln(7.39) + j * 1.005
Using a scientific calculator or a calculator that supports natural logarithm (ln), you can find the approximate value of ln(7.39), and the result will be:
loge(Z) ≈ 1.999 + j * 1.005
Learn more about natural logarithm here:
https://brainly.com/question/29154694
#SPJ11
Packaging for a new type of cheese is being constructed in the shape of a right triangular prism. the cheesemaker wants the volume of the packaging to be 54 mm3. if the height of the cheese is 2 mm less than twice the base and length is 3 mm longer than twice the base, what must the base of the packaging be? (note: the volume of a right triangular prism is v = 1/2bhl.)
Answers
The base of the packaging will be,x =3.35 mm. The volume right triangular prism is 54 mm³
What is the definition of a triangular prism?Join the edges of three rectangles. Now, from both ends, seal their triangle mouths. A triangular prism is a name for the form.
The volume of the packaging(right triangular prism) = 54 mm³
Height of the cheese(H)= 2 mm-2x
Length(L)=3+2x
The volume of a right triangular prism is v = 1/2bhl
\(\rm V = \frac{1}{2} \times b \times h \times \\\\ 108 = 6+4x-6x-4x^2 \\\\ x=3.35\)
Hence, the base of the packaging will be,x =3.35 mm.
To learn more about triangular prisms refer to:
https://brainly.com/question/16261758
#SPJ1
a town that recently started a single-stream recycling program provided 60-gallon recycling bins to 25 randomly selected households and 75-gallon recycling bins to 22 randomly selected households. the total volume of recycling over a 10-week period was measured for each of the households. the average total volumes were 382 and 415 gallons for the households with the 60- and 75-gallon bins, respectively. the sample standard deviations were 52.5 and 43.8 gallons, respectively. assume that the 10-week total volumes of recycling are approximately normally distributed for the populations of both groups with unknown and unequal population standard deviations. construct a 98% confidence interval for the difference in the mean volumes of 10-week recycling for all households with the 60- and 75-gallon bins
Answers
The 98% "confidence-interval" for which the difference in mean volumes of 10-week recycling for all households with 60 , 75-gallon bins is (-66.886, 0.886).
In order to construct the confidence-interval for the difference in the mean-volumes of 10-week recycling for all households with the 60- and 75-gallon bins, we can use the two-sample t-test with unequal variances.
Let μ₁ and μ₂ be the true mean volumes of recycling for all households with the 60- and 75-gallon bins, respectively.
We want to estimate the difference in the means, μ₁ - μ₂, with a 98% confidence interval.
First, we calculate sample means and standard-deviations;
x'₁ = 382 gallons, s₁ = 52.5 gallons (for 60-gallon bins)
x'₂ = 415 gallons, s₂ = 43.8 gallons (for 75-gallon bins)
Next, we calculate "standard-error" of difference in the means;
SE(μ₁ - μ₂) = √(s₁²/n₁ + s₂²/n²₂);
where n₁ = 25 and n₂ = 22 are the sample sizes.
Substituting the values,
We get,
SE(μ₁ - μ₂) = √((52.5)²/25 + (43.8)²/22) = 14.05 gallons,
The "critical-value" for a 98% confidence interval with (n₁-1) + (n₂-1) = 45 degrees of freedom is : t = 2.412,
The confidence interval can be written as : (x'₁ - x'₂) ± t × SE(μ₁ - μ₂),
Substituting the values,
We get,
= (382 - 415) ± 2.412 × 14.05,
= -33 ± 33.886,
= (-33-33.886, -33+33.886) = (-66.886, 0.886).
Therefore, the required 98% confidence-interval is (-66.886, 0.886).
Learn more about Confidence Interval here
https://brainly.com/question/23639280
#SPJ4
Create and solve the EQUATION. 4. The sum of seven times a number and 16 is 163.
Answers
An equation for this statement "The sum of seven times a number and 16 is 163," is 7n + 16 = 163.
The solution is 21.
How to determine the two unknown numbers?In order to solve this word problem, we would assign a variable to the unknown number, and then translate the word problem into an algebraic equation as follows:
Let the variable n represent the unknown number.
Based on the statement "The sum of seven times a number and 16 is 163," we can logically deduce the following algebraic equation;
7n + 16 = 163
7n = 163 - 16
7n = 147
n = 147/7
n = 21.
Read more on equation here: brainly.com/question/18912929
#SPJ4
a randomly generated list of numbers from 0 to 5 is being used to simulate an event. the numbers 0, 1, and 2 represent a success. what is the estimated probability of a success?
Answers
Answer:
The probability of a success can be calculated by dividing the number of successes by the total number of trials.
In this case, the number of successes is the sum of the occurrences of the numbers 0, 1, and 2. These numbers occur with equal probability, so the total number of occurrences of these numbers is:
3 * (1/6) = 1/2
This means that the probability of a success is:
P(success) = # of successes / total # of trials = (1/2) / 1 = 1/2
Therefore, the estimated probability of a success is 0.5 or 50%.
To estimate the probability of a success in this scenario, we need to determine the proportion of the randomly generated numbers that represent a success. Since the numbers 0, 1, and 2 represent a success, out of the possible six numbers (0, 1, 2, 3, 4, and 5), there are three that correspond to a success. Therefore, the estimated probability of a success is 3/6 or 0.5.
It is important to note that this is only an estimated probability, as it is based on a simulation and not a true experiment with a large sample size. The actual probability of a success may differ slightly from this estimate.
In order to obtain a more accurate estimate, we would need to perform multiple simulations and calculate the proportion of successes across all of the trials. This would give us a better idea of the true probability of a success in this scenario.
Additionally, it is important to consider the context of the event being simulated and whether or not this estimated probability is sufficient for the desired outcome. If a success rate of 50% is not acceptable, alternative methods may need to be explored to increase the likelihood of success.
For more questions on probability
https://brainly.com/question/24756209
#SPJ11
Please don't reply if you know the answer. it's due in 8 minutes.
The product of x and 7 is not greater than 10
A.) 7x > 10
B.) 7/x < 10
C.) 7 + 4 < 10
D.) 7x <= 10
Answers
answer is D) 7x < 10
$131,701. 32 is what percent of $790,207. 91?
Answers
To find the percentage, we can use the following formula:
Percentage = (Part / Whole) * 100
So, $131,701.32 is approximately 16.67% of $790,207.91.
In this case, the part is $131,701.32 and the whole is $790,207.91.
Percentage = ($131,701.32 / $790,207.91) * 100
Calculating the value:
Percentage ≈ 0.1667 * 100
Percentage ≈ 16.67%
Therefore, $131,701.32 is approximately 16.67% of $790,207.91.
Alternatively, we can calculate the percentage by dividing the part by the whole and multiplying by 100:
Percentage = ($131,701.32 / $790,207.91) * 100 ≈ 0.1667 * 100 ≈ 16.67%
So, $131,701.32 is approximately 16.67% of $790,207.91.
If you have any further questions, feel free to ask!
Learn more about Percentage here
https://brainly.com/question/24877689
#SPJ11
let ~u and ~v be vectors in three dimensional space. if ~u ×~v = ~0, then ~u = ~0 or ~v = ~0. state if this is true or false. explain why.
Answers
The statement is true because if the cross product of two vectors ~u and ~v in three-dimensional space is equal to the zero vector ~0, then it implies that either ~u or ~v is equal to the zero vector ~0.
The cross product ~u × ~v produces a vector that is perpendicular (orthogonal) to both ~u and ~v. If the resulting cross product is the zero vector ~0, it means that ~u and ~v are either parallel or collinear.
If ~u and ~v are parallel or collinear, it implies that they are scalar multiples of each other. In this case, one of the vectors can be expressed as a scaled version of the other. Consequently, either ~u or ~v can be the zero vector ~0.
Learn more about vectors https://brainly.com/question/29740341
#SPJ11
17. The record low temperature in Missouri was −40°F, set February 13, 1905. The record high temperature of 118°F was set July 14, 1954, in the same city: Warsaw, Missouri. The Missouri mean temperature is 55°F. Determine whether the record high or the record low is closer to the mean temperature than the other record, and how much closer is it? Make sure you show your work to support your answer.
Answers
Answer:
The record high temperature of 118°F is 63°F higher than the mean temperature of 55°F. The record low temperature of -40°F is 95°F lower than the mean temperature of 55°F. The record high temperature of 118°F is closer to the mean temperature than the record low temperature of -40°F by 32°F.
toby's school is 4 miles west of his house and 3 miles south of his friend erica's house. every day, toby bicycles from his house to his school. after school, he bicycles from his school to erica's house. before dinner, he bicycles home on a bike path that goes straight from erica's house to his own house. how far does toby bicycle each day?
Answers
Toby cycles 12 miles each day.
To find out how far Toby cycles each day, we need to add up the distance he covers during his morning and afternoon trips. Here are the steps we need to follow:
Step 1: Determine Toby's cycling distance from his house to his schoolDistance from Toby's house to his school = 4 miles west. Toby bicycles this distance every day. Therefore, his one-way cycling distance from home to school is 4 miles.
Step 2: Determine Toby's cycling distance from his school to Erica's house.Distance from Toby's school to Erica's house = 3 miles south. Toby cycles this distance every day after school. Therefore, his one-way cycling distance from school to Erica's house is 3 miles.
Step 3: Determine Toby's cycling distance from Erica's house to his house.Distance from Erica's house to Toby's house = we don't know. But we know that Toby takes a bike path that goes straight from Erica's house to his own house. Therefore, we can assume that the distance from Erica's house to Toby's house is the hypotenuse of a right-angled triangle with legs of 3 miles (south) and 4 miles (west).
We can use the Pythagorean Theorem to find the hypotenuse: c2 = a2 + b2c2 = 32 + 42c2 = 9 + 16c2 = 25c = √25c = 5 milesTherefore, Toby cycles 5 miles every day on his bike path from Erica's house to his own house.Step 4: Add up Toby's one-way cycling distances to find out how far he cycles each day.Toby's one-way cycling distance from home to school = 4 milesToby's one-way cycling distance from school to Erica's house = 3 milesToby's one-way cycling distance from Erica's house to his house = 5 milesTotal cycling distance = 4 + 3 + 5Total cycling distance = 12 miles.
To know more about Pythagorean Theorem refer to-
brainly.com/question/14930619#
#SPJ11
The points (2, 5) and (1, 1) fall on a particular line. What is its equation in slope-intercept form?
Write your answer using integers, proper fractions, and improper fractions in simplest form.
y=
x-
Answers
A museum is holding painting classes for teenage girls next week.They are charging a $38 flat fee plus $2 per picture. If Rosa has $304 to spend, which equation represents how many pictures she can paint?
a.38B+ 2 = 304
b.2B + 38 = 304
c.2B-38=304
d.2B+304 = 38
Answers
How many ordered quadruplets (a1,a2,a3,a4) of non-negative integers, where at least one of the integers is even, satisfy the equation a1+a2+a3+a4=100 ? Please express your answer in the form (wx)−(yz). (Note that the values of w,x,y and z will be integers, but not necessarily all distinct.)
Answers
The number of ordered quadruplets of non-negative integers that satisfy the given condition is:
|A| - |B| = 161,700 - 16,215 = 145,485
To solve this problem, we need to use the Principle of Inclusion-Exclusion (PIE). Let A be the set of all quadruplets (a1,a2,a3,a4) of non-negative integers that satisfy the equation a1+a2+a3+a4=100, and let B be the set of all quadruplets where all four integers are odd. Then the number of quadruplets that satisfy the given condition is given by:
|A| - |B|
To find |A|, we can use stars and bars. If we consider 100 stars and 3 bars, we can partition the stars into 4 groups, corresponding to the four integers. There will be 99 gaps between the stars and bars, and we need to choose 3 of them to place the bars. This gives us:
|A| = (99 choose 3) = 161,700
To find |B|, we can use a similar approach. If all four integers are odd, then they must be of the form 2k+1, where k is a non-negative integer. Substituting this into the equation a1+a2+a3+a4=100, we get:
2k1 + 1 + 2k2 + 1 + 2k3 + 1 + 2k4 + 1 = 100
Simplifying this equation, we get:
k1 + k2 + k3 + k4 = 48
This is now an equation in non-negative integers, which we can solve using stars and bars. We need to partition 48 stars into 4 groups, and there will be 3 bars separating them. This gives us:
|B| = (47 choose 3) = 16,215.
Learn more about Inclusion-Exclusion (PIE) here:
https://brainly.com/question/10927267
#SPJ11
a common everyday counting unit that is used to mean 12 of an object is a____
Answers
A common everyday counting unit that is used to mean 12 of an object is a Dozen
Dozen is derived from the Old French word "douzaine" which means twelve each. In most situations, a dozen is used to refer to a group of twelve items. The term dozen is also used in informal situations to refer to a very large number of objects. For example, one might say "I have dozens of friends!" to mean that they have a lot of friends.
Dozen is a useful term when counting items. It allows for large numbers to be easily broken down into manageable groups. For example, if you have 120 pencils, you could easily count them by saying that you have 10 dozen pencils. It can also be useful when talking about fractions. For example, instead of saying "one and a half of an item," one could say "one and a half dozen of an item."
Dozen is a common everyday counting unit that is used to mean 12 of an object. It is a useful term when counting items and when talking about fractions, and can be used in both formal and informal settings.
Know more about a Dozen here :
https://brainly.com/question/30948187
#SPJ11
um..can someone tell me how to choose the brainliest answer? i don't know how I'm new >
Answers
Answer:
you press/click the small crown icon below the user's answer
Step-by-step explanation:
assume the random variable x is normally distributed with mean μ=90 and standard deviation σ=15. compute the probability p(x>102)
Answers
The probability that x is greater than 102 is approximately 0.2119.
We need to standardize the random variable x before finding the required probability.
The standardized random variable Z is given by:
Z = (x - μ) / σ
Here, x = 102, μ = 90, and σ = 15.
So,
Z = (102 - 90) / 15 = 0.8
Now, we need to find P(Z > 0.8). We can use a standard normal distribution table or calculator to find this probability.
Using a standard normal distribution table, we find that the probability of Z being greater than 0.8 is approximately 0.2119.
Therefore,
P(x > 102) = P(Z > 0.8) ≈ 0.2119
So, the probability that x is greater than 102 is approximately 0.2119.
To know more about probability refer here:
https://brainly.com/question/11234923
#SPJ11
how many combinations from 4 entrees, 6 vegetables, and 6 deserts if you can pick only 1 entree,2 vegetables, and 1 desert
Answers
There are 144 combinations of 1 entree, 2 vegetables, and 1 dessert that can be selected from 4 entrees, 6 vegetables, and 6 desserts.
To determine the number of combinations, we multiply the number of options for each category.
For the entree, we have 4 options to choose from.
For the vegetables, we need to select 2 out of 6, which can be done in 6 choose 2 ways.
This is calculated as 6! / (2!(6-2)!), which simplifies to
6! / (2!4!)
Similarly, for the dessert, we have 6 options to choose from.
To calculate 6 choose 2, we can use the formula for combinations:
n choose r = n! / (r!(n-r)!).
Plugging in the values, we have
6! / (2!4!) = (6 × 5 × 4 × 3 × 2 × 1) / [(2 × 1) × (4 × 3 × 2 × 1)] = 15.
Therefore, we have 4 options for the entree, 15 options for the vegetables, and 6 options for the dessert.
Multiplying these numbers together, we get 4 × 15 × 6 = 144.
Therefore, there are 144 possible combinations of 1 entree, 2 vegetables, and 1 dessert, given the options of 4 entrees, 6 vegetables, and 6 desserts.
Learn more about combinations here:
https://brainly.com/question/28065038
#SPJ11
A manager of a deli gathers data about the number of sandwiches sold based on the number of customers who visited the deli over several days. The
table shows the data the manager collects, which can be approximated by a linear function.
Customers
104
70
111
74
170
114
199
133
163
109
131
90
Sandwiches
If, on one day, 178 customers visit the deli, about how many sandwiches should the deli manager anticipate selling?
Answers
To estimate the number of sandwiches the deli manager should anticipate selling when 178 customers visit the deli, we can analyze the given data and approximate it using a linear function.
By observing the table, we notice that the number of sandwiches sold varies with the number of customers. This indicates a relationship between the two variables.
To estimate the number of sandwiches, we can fit a line to the data points and use the linear function to make predictions. Using a statistical software or a spreadsheet, we can perform linear regression analysis to find the equation of the best-fit line. However, since we are limited to text-based interaction, I will provide a general approach.
Let's assume the number of customers is the independent variable (x) and the number of sandwiches is the dependent variable (y). Using the given data points, we can calculate the equation of the line.
After calculating the linear equation, we can substitute the value of 178 for the number of customers (x) into the equation to estimate the number of sandwiches (y).
Please provide the data points for the number of sandwiches sold corresponding to each number of customers so that I can perform the linear regression analysis and provide a more accurate estimate for you.
Learn more about selling here
https://brainly.com/question/29136043
#SPJ11
ten men clear a field of area 10 hectares in four days. How many hectares would 15 men clear in six days?
Answers
Answer:
22.5
Step-by-step explanation:
4 days=15
2days=7.5
6=22.5
Evaluate the integral using trig sub ∫ x 4
x 2
+16
dx 16x 3
(x 2
+16) 3/2
+C b. − 48x 3
(x 2
+16) 3/2
+C c. − 16x 3
(x 2
+16) 3/2
+C d. 48x 3
(x 2
+16) 3/2
+C
Answers
The correct answer is c. − 16x^3 / ((x^2 + 16)^(3/2)) + C. To evaluate the integral, we substitute x = 4tan(t) as explained earlier.
The integral simplifies to:
∫ x^4 / ((x^2 + 16)^(3/2)) dx = ∫ (16tan^4(t)) / (16sec^3(t)) sec^2(t) dt
= ∫ tan^4(t) / sec(t) dt.
Using the trigonometric identity tan^2(t) = sec^2(t) - 1, we have:
∫ tan^4(t) / sec(t) dt = ∫ (sec^2(t) - 1)^2 / sec(t) dt
= ∫ (sec^4(t) - 2sec^2(t) + 1) / sec(t) dt
= ∫ sec^3(t) - sec(t) dt.
Integrating each term separately, we obtain:
∫ sec^3(t) dt = (1/2)sec(t)tan(t) + (1/2)ln|sec(t) + tan(t)| + C.
Finally, substituting back x = 4tan(t), we get:
∫ x^4 / ((x^2 + 16)^(3/2)) dx = (1/2)sec(t)tan(t) + C.
Using the relationship sec(t) = sqrt(x^2 + 16) / 4 and tan(t) = x / 4, we can rewrite the answer as c. − 16x^3 / ((x^2 + 16)^(3/2)) + C.
Learn more about integral here:
https://brainly.com/question/31109342
#SPJ11
In the coordinate plane, the points X9, 5, Y−−3, 6, and Z−8, 4 are reflected over the x-axis to the points X′, Y′, and Z′, respectively. What are the coordinates of X′, Y′, and Z′?
Answers
Answer:
When a point is reflected over the x-axis, the x-coordinate remains the same, but the y-coordinate is multiplied by -1.
So, the coordinates of X' are (9, -5) since the x-coordinate remains the same and the y-coordinate is multiplied by -1.
Similarly, the coordinates of Y' are (-3, -6) and the coordinates of Z' are (-8, -4).
Therefore, X′ is (9,−5), Y′ is (−3,−6), and Z′ is (−8,−4).
John is saving to buy a new car that will cost him $24,000. John started his savings at the beginning of the school year and has been able to accumulate $1000 after the first month. John plans to continue his savings at a rate proportional to the amount he still needs to save. Determine John's savings amount as function of time Hint: A variable y is said to be proportional to a variable x if y=cx for some constant c.
Answers
John's savings amount as a function of time is S(t) = $24,000 / 25. Initially, he needs to save $24,000 for a new car. After the first month, he has saved $1,000. The savings amount is directly proportional to the time elapsed. The constant of proportionality is 1/24. Thus, John's savings amount can be determined based on the remaining amount he needs to save.
John's savings amount can be represented as a function of time and is proportional to the amount he still needs to save. Let's denote the amount John needs to save as N(t) at time t, and his savings amount as S(t) at time t. Initially, John needs to save $24,000, so we have N(0) = $24,000.
We know that John has saved $1,000 after the first month, which means S(1) = $1,000. Since his savings amount is proportional to the amount he still needs to save, we can write the proportionality as:
S(t) = k * N(t)
where k is a constant of proportionality.
We need to find the value of k to determine John's savings amount at any given time.
Using the initial values, we can substitute t = 0 and t = 1 into the equation above:
S(0) = k * N(0) => $1,000 = k * $24,000 => k = 1/24
Now we have the value of k, and we can write John's savings amount as a function of time:
S(t) = (1/24) * N(t)
Since John's savings amount is proportional to the amount he still needs to save, we can express the amount he still needs to save at time t as:
N(t) = $24,000 - S(t)
Substituting the expression for N(t) into the equation for S(t), we get:
S(t) = (1/24) * ($24,000 - S(t))
Simplifying the equation, we have:
24S(t) = $24,000 - S(t)
25S(t) = $24,000
S(t) = $24,000 / 25
Therefore, John's savings amount at any given time t is S(t) = $24,000 / 25.
To know more about proportional savings, refer here:
https://brainly.com/question/29251832#
#SPJ11
