Are the data shown in this line plot skewed left, skewed right, or not skewed? skewed right skewed left not skewed
Answers
Answer:
where is the picture
Step-by-step explanation:
Related Questions
Please help
fraction in simplest form...

Answers
Answer:
the answer is 1
Step-by-step explanation:
Using the graph, determine the positive and negative interval. Your answer can be written as an inequality or in interval notation. Make sure to label which answer is the positive interval and negative interval. HELP ASAP PLEASE

Answers
which list shows how many equal-sized groups of 28 students Ms. Lee can make?
*Picture Attached*
*Greatest Common Factor*

Answers
Answer:
1,2,3,4 or 6
Step-by-step explanation:
A bag of jelly beans contains 20 blue jelly beans, 52 yellow jelly beans, 34 green jelly beans, 71 orange jelly beans, and 23 red jelly beans. What percentage of the jelly beans are yellow?
Answers
Answer: 26%
Step-by-step explanation:
20+52+34+71+23= 200
52/200 = 26/100
Answer:
26% of the jelly beans are yellow
Step-by-step explanation:
To find this we add up all the jelly beans which is 200 jelly beans
Then we divide it by the number of yellow jelly beans which is 52/200
which then equals .26. In a percentage that is 26%
Help me please il give 20 points!



Answers
Answer: 1. a. 15 b. 11 c. 2 d. 7 e. 5.5
2. Stem: Leaf:
1 9
2 5, 9
3 3, 3, 8
4 0, 7, 9
5 4, 5
6 1, 5
7 2, 7
8 1
3. a. 13 inches b. I'm pretty sure that it is the second quarter because there is more snow. c. The first quarter because it's section is more spread out among the numbers.
Step-by-step explanation:
2. Stem:
Leaf:
9
2
5, 9
3
3, 3, 8
4
0, 7, 9
5
4, 5
6
1,5
7
2, 7
8
1
3. a. 13 inches
b. I'm pretty sure that it is
the second quarter because there is more show.
c. The first quarter because it's
section is more spread out among the numbers.
Step-by-step explanation:
Use the graph to determine the end behavior for the linear function. HELP ASAP PLEASE
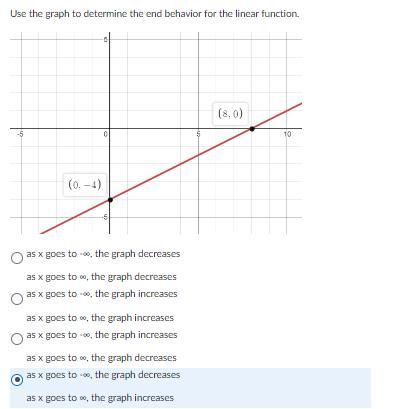
Answers
Answer:
You have the correct answer.
"as x goes to -infinity the graph decreases
as x goes to infinity the graph increases"
Step-by-step explanation:
Drag the tiles to the correct boxes to complete the pairs.
Match the pairs of coordinates with the distances between them.

Answers
The pairs of coordinates should be matched with the distances between them should be matched as follows;
Pairs Distance
(4, 2) and (1, -2) → 5 units.
(-8, 7) and (2, -3) → √200 units.
(9, 1) and (1, 9) → √128 units.
(-2, -6) and (-8, 2) → 10 units.
How to calculate the distance on coordinates?Mathematically, the distance between two (2) points that are on a coordinate plane can be calculated by using this formula:
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
For the ordered pairs (4, 2) and (1, -2), we have;
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance = √[(1 - 4)² + (-2 - 2)²]
Distance = √[(-3)² + (-4)²]
Distance = √(9 + 16)
Distance = √25
Distance = 5 units.
For the ordered pairs or points (-8, 7) and (2, -3), we have;
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance = √[(2 + 8)² + (-3 - 7)²]
Distance = √[(10)² + (-10)²]
Distance = √(100 + 100)
Distance = √200 units.
For the ordered pairs or points (9, 1) and (1, 9), we have;
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance = √[(1 - 9)² + (9 - 1)²]
Distance = √[(-8)² + (8)²]
Distance = √(64 + 64)
Distance = √128 units.
For the ordered pairs or points (-2, -6) and (-8, 2), we have;
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance = √[(-8 + 2)² + (2 + 6)²]
Distance = √[(-6)² + (8)²]
Distance = √(36 + 64)
Distance = √100
Distance = 10 units.
Read more on distance here: brainly.com/question/12470464
#SPJ1
pls help with this assignment D:
Answers
Answer:
ok, i don't remember this math but! all the questions it ask count the beans count like on , 3/8 count as u see it says 4. and with adding that i dont have time to do um here.
Step-by-step explanation:
1.4 2.3 3.5 4.1 5.1 6.14? if wrong im tired but for next time count and add i think
Please helpp!! Ty ty!♡♡

Answers
Answer:
25
Step-by-step explanation:
4a +12 -2c + c
4( ) + 12 - 2( ) + ( )
4(4) + 12 - 2(3) + 3
16 + 12 - 6 + 3
28 - 6 + 3
22 + 3
25
Helping in the name of Jesus.
Therefore, 4a + 12 - 2c + c = 25
Step-by-step explanation:a = 4
c = 3
Swap letters for numbers:4a + 12 - 2c + c
(4)(4) + 12 - (2)(3) + 3
16 + 12 - (2)(3) + 3
28 - (2)(3) + 3
28 - 6 + 3
22 + 3 = 25
Draw a conclusion:
Hence your answer is:4a + 12 - 2c + c = 25
I hope this helps!
GIVING BRAINLIEST
Find the area of the circle if r = 5 meters. Leave the answer in terms of
A =1000 square meters
B)
A =251 square meters
C)
A = 51 square meters
D)
A = 101 square meters

Answers
Answer:
The area is 78.54 square meters
Step-by-step explanation:
The area = pi*r² r=5
A=pi*25
A≈78.54 square meters
The function ƒ(x) = {(1, 2), (2, 4), (3, 6), (4, 8)} can be represented in several other ways. Which is NOT a correct representation of the function ƒ(x)?
- other two options -
x is a natural number less than 5 and y is twice x
y = 2x and the domain is {1, 2, 3, 4}


Answers
Answer:
The graph is wrong.
Step-by-step explanation:
The y and x dont correlate with the right information, meaning it goes 2, 1 4,3 instead of 1, 2 2, 4
Expression Name Expression E 3.8 + 0 F 0 + 0.5 G –8 + 0 H 9 ÷ 0 The table above shows four numeric expressions. Which expression is an integer when it's evaluated? Question 2 options: A) H B) E C) F D) G
Answers
Answer:
D) G
Step-by-step explanation:
E evaluates to 3.8 +0 = 3.8 . . . not an integer
F evaluates to 0 +0.5 = 0.5 . . . not an integer
G evaluates to -8 +0 = -8 . . . an integer
H evaluates to 9/0 = undefined . . . not an integer
__
Expression G evaluates to an integer.
The volume of a cylinder is 630 cubic centimeters. What is the volume of a similar cylinder that has been reduced by a scale factor of 13
? round to your nearest tenth place
Answers
Answer:
Step-by-step explanation:
ifddergfergwrtg
Ans = 48.5 (nearest tenth)
find the missing letter N if the width is 2ft and the area equal 28 sq ft
Answers
Answer:
Step-by-step explanation:
Area = 28 Sq.ft
length * width = 28
2 * n = 28
Divide both sides by 2
2n/2 = 28/2
n = 14 ft
Combine like terms in the expression 2a-3b+5b-a
Answers
Answer: a= -2b
Step-by-step explanation:
Simplifying
2a + -3b + 5b + -1a = 0
Reorder the terms:
2a + -1a + -3b + 5b = 0
Combine like terms: 2a + -1a = 1a
1a + -3b + 5b = 0
Combine like terms: -3b + 5b = 2b
1a + 2b = 0
Solving
1a + 2b = 0
Solving for variable 'a'.
Move all terms containing a to the left, all other terms to the right.
Add '-2b' to each side of the equation.
1a + 2b + -2b = 0 + -2b
Combine like terms: 2b + -2b = 0
1a + 0 = 0 + -2b
1a = 0 + -2b
Remove the zero:
1a = -2b
Divide each side by '1'.
a = -2b
Simplifying
a = -2b
Answer:
a + 2b
Step-by-step explanation:
You want to combine like terms in 2a-3b+5b-a.
Like termsLike terms are terms that have the same variables. All of the 'a' terms are like terms, and all of the 'b' terms are like terms. It can be useful to rearrange the expression so like terms are adjacent to each other.
= 2a -a -3b +5b
= a(2 -1) +b(-3 +5) . . . . . distributive property
= a(1) +b(2) . . . . . . . . . do the addition/subtraction
= a +2b
In the class election, the student who gets the highest number of votes will become the class president and the one who gets the second highest number of votes will become the class vice president. Tabitha and four other students were candidates. Tabitha’s teacher announces the election results as percentages of the total number of votes. Two hundred votes were cast in the election. In this activity, you will relate the percentages of the votes received to the actual numbers.
Question 1
The table gives the percentage of votes each candidate received. Use the information in the table to understand the results of the election.
Candidate Percentage of Votes
Tabitha 30%
Vincent 12%
Esmeralda 22%
Nancy 5%
Tyler 31%
Answers
Answer: Tyler for first and Tabitha for second
Step-by-step explanation: if you have 100% then the percentage would just be itself to 30% would be 30 and 12% would be 12 and 22% would be 22 and 5% would be 5 and 31% would be 31 so the Class president would be Tyler and the vice president would be Tabatha
help please I'll mark brainliest

Answers
Answer:
q1 -10
q2c
Step-by-step explanation:
2qC is the answer
A store sells books for $12 each. In the proportional relationship between x, the number of books purchased, and y, the cost per books in dollars" to "y, the total cost of the books in dollars, the constant of proportionality is 12. Which equation shows the relationship between x and y?
Answers
Answer:
Y=12x
If Y represents the Cost and X represents the number of books purchased.
WORD FORM:
Cost equals 12 times as many books that are purchased.
Help me with these two questions ASAP (I will try to mark brainliest)


Answers
Answer:
1. C
2.B
IG
Step-by-step explanation: CALCULATE
Answer:
the answer would be a is correct
Worth 15 pts.
Choose the correct answer

Answers
Answer:
Its c. c = 50.
Step-by-step explanation:
First, we need to figure out what the equation equals.
7 + 7/7 + 7*7 - 7 = x
PEMDAS
Parentheses, exponents, division/fraction, addition, subtraction.
7/7 = 1. So equation changed into 7 + 1 + 7*7 - 7 = x.
7*7 = 49. So equation changed again into 7 + 1 + 49 - 7.
Lets calculate it. 7 + 1 = 8 + 49 = 57 - 7 = 50. x = 50.
c is the only one who has a calculation of 50.
Select all of the following that are quadratic equations.
(MULTIPLE CHOICE)
A). 3 x² + 5 x - 7 = 0
B). 5 x² + 15 x = 0
C). 2 x - 1 = 0
D). x² - 4 x = 4 x + 7
E). 6 x - 1 = 4 x + 7
F). x³ - 2 x² + 1 = 0
Answers
Answer:
A B D F
Step-by-step explanation:
quadratic equation normally comes with squares
What is the equation for the line intercept form?

Answers
Answer:
Step-by-step explanation:
y = mx + b
Please help and explain you answer please!

Answers
Answer:
90 houses
Step-by-step explanation:
you would multiply the amount of houses cleaned by the decimal form of the percentage given.
x-2y=3, x^2-2y=3, x^2-2xy+4y^2=11, find the value of x^2y-2xy^2
Answers
This is a system of three equations with two unknowns, x and y. To solve it, we can use the method of elimination. First, we can eliminate y by subtracting the first equation from the second equation:
x^2-2y=3 - (x-2y=3) => x^2-x=0
Then we can factor the resulting equation and find the values of x:
x^2-x=0 => x(x-1)=0 => x=0 or x=1
Next, we can substitute these values of x into any of the original equations and find the corresponding values of y. For example, using the first equation:
x-2y=3 => 0-2y=3 => y=-3/2 when x=0 x-2y=3 => 1-2y=3 => y=-1 when x=1
Finally, we can substitute these values of x and y into the expression x2y-2xy2 and evaluate it:
x2y-2xy2 => 02(-3/2)-2(0)(-3/2)2 => 0 when x=0 and y=-3/2 x2y-2xy2 => 12(-1)-2(1)(-1)2 => -3 when x=1 and y=-1
Therefore, the value of x2y-2xy2 can be either 0 or -3 depending on the values of x and y.
Write the equation of the line in slope-intersect from
The coefficients in the equation are b=4 and m=-5
Answers
Answer:
y=-5x+4
Step-by-step explanation:
y=mx+b is slope-intercept form.
Plug in -5 for m and 4 for b.
The equation we're left with is y=-5x+4
Trust me I took algebra in 7th, and passed.
What is the domain and range of:

Answers
Answer:
b
Step-by-step explanation:
how it works with life
The estimated average speed you found earlier in the lesson was 30 miles per hour. How does your estimated speed compare to the speed you just computed?
Answer in 2 complete sentences.
Answers
Divide the total distance traveled by the total time spent traveling. Your estimated speed should be reletively close to your calculated speed.
(please give brainliest)
Sanjay went blueberry picking along a 3-mile walking path. He picked blueberries steadily along the walk. When he was finished, he had collected 50 ounces of blueberries.
How many ounces of blueberries did Sanjay pick each mile?
Write your answer as a proper fraction or mixed number.
Answers
Answer:
16 2/3 per a mile
Step-by-step explanation:
50 ounces of blueberries/3 miles = 16.666 repeated
16.666 repeated = 16 2/3 ounces/mile
Answer: Sanjay picked 16.66 ounces each mile
Step-by-step explanation:
For this exercise let "x" represents the amount of ounces of blueberries that Sanjay picked each mile, along the 3-mile walking path.
According to the information given in the exercise, you know that Sanjay picked a total amount of 50 ounces of blueberries along the walking path.
Then, knowing that the length of that walking path is 3 miles, you can set up the following proportion:
\(\frac{3}{50} = \frac{1}{x}\)
Now, the next step is to solve for "x" in order to find its value.
You get that this is:
\((x)(\frac{3}{50} )=1\\\\x=(1)(\frac{3}{50} )\\\\x=16.66\)
Therefore, knowing the value of "x", you can conclude that Sanjay picked 16.66 ounces of blueberries each mile.
16.66 = 16 2/3
Find all possible values of a such that ax² + (2a + 2)x + a + 3 = 0 has two roots and the distance between them on the number line is greater than 1.
Answers
Answer:
\(-2\sqrt{2}-2 < a < 2\sqrt{2}-2,\;\;a\neq0\)
Step-by-step explanation:
Given quadratic equation:
\(ax^2 + (2a + 2)x + a + 3 = 0\)
To find the possible values of "a" such that the given equation has two roots and the distance between them on the number line is greater than 1, use the quadratic formula.
\(\boxed{\begin{minipage}{4 cm}\underline{Quadratic Formula}\\\\$x=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}\)
Comparing the coefficients:
\(a = a\)\(b = (2a + 2)\)\(c = (a + 3)\)Substitute the coefficients into the quadratic formula:
\(x=\dfrac{-(2a+2) \pm \sqrt{(2a+2)^2-4a(a + 3)}}{2a}\)
Simplify the discriminant (the part under the square root sign):
\(x=\dfrac{-(2a+2) \pm \sqrt{-4a+4}}{2a}\)
Factor out 4 from the discriminant:
\(x=\dfrac{-(2a+2) \pm \sqrt{4(-a+1)}}{2a}\)
\(\textsf{Apply the radical rule:} \quad \sqrt{ab}=\sqrt{a}\sqrt{b}\)
\(x=\dfrac{-(2a+2) \pm \sqrt{4}\sqrt{-a+1}}{2a}\)
Therefore:
\(x=\dfrac{-(2a+2) \pm 2\sqrt{-a+1}}{2a}\)
Factor out the common term 2:
\(x=\dfrac{-(a+1)\pm \sqrt{-a+1}}{a}\)
Therefore, the two solutions are:
\(x=\dfrac{-a-1+\sqrt{-a+1}}{a},\;\;x=-\dfrac{a+1+\sqrt{-a+1}}{a}\)
As both solutions have "a" as their denominator, a ≠ 0.
Note: When substituting a = 0 into the original equation, we are left with a linear equation, which only has one root. Therefore, this confirms that a ≠ 0.
Now we have found expressions for the two roots, we can set the distance between them to greater than 1:
\(\dfrac{-a-1+\sqrt{-a+1}}{a}-\left(-\dfrac{a+1+\sqrt{-a+1}}{a}\right) > \:1\)
\(\dfrac{-a-1+\sqrt{-a+1}}{a}+\dfrac{a+1+\sqrt{-a+1}}{a} > \:1\)
Simplify:
\(\begin{aligned}\dfrac{-a-1+\sqrt{-a+1}+a+1+\sqrt{-a+1}}{a}& > 1\\\\\dfrac{2\sqrt{-a+1}}{a}& > 1\\\\2\sqrt{-a+1}& > a\\\\(2\sqrt{-a+1})^2& > a^2\\\\4(-a+1)& > a^2\\\\-4a+4& > a^2\\\\a^2+4a-4& < 0\\\\(a+2)^2-8& < 0\\\\(a+2)^2& < 8\end{aligned}\)
\(\textsf{For\;\;$u^n < a$,\;\;if\;$n$\;is\;even\;then\;\;$-\sqrt[n]{a} < u < \sqrt[n]{a}|$:}\)
\(-\sqrt{8} < a+2 < \sqrt{8}\)
Therefore:
\(-\sqrt{8} -2 < a < \sqrt{8}-2\)
\(-2\sqrt{2}-2 < a < 2\sqrt{2}-2\)
So the possible values of "a" such that ax² + (2a + 2)x + a + 3 = 0 has two roots and the distance between them on the number line is greater than 1 are:
\(\large{\boxed{-2\sqrt{2}-2 < a < 2\sqrt{2}-2,\;\;a\neq0}\)
The stem-and-leaf plot displays data collected on the size of 15 classes at two different schools.
Bay Side School Seaside School
8, 6, 5 0 5, 8
8, 6, 5, 4, 2, 0 1 0, 1, 2, 5, 6, 8
5, 3, 2, 0, 0 2 5, 5, 7, 7, 8
3 0, 6
2 4
Key: 2 | 1 | 0 means 12 for Bay Side and 10 for Seaside
Part A: Calculate the measures of center. Show all work. (2 points)
Part B: Calculate the measures of variability. Show all work. (1 point)
Part C: If you are interested in a smaller class size, which school is a better choice for you? Explain your reasoning. (1 point)
PLEASE HELP ASAP !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Answers
Part A: To calculate the measures of center, we can find the median and the mean for each school.
For Bay Side School, the median class size is the average of the 8th and 9th values when the data is sorted in ascending order. The 8th and 9th values are both 25, so the median class size is 25.
To find the mean class size for Bay Side School, we can add up all the class sizes and divide by the total number of classes. The sum of the class sizes is 12 + 12 + 12 + 14 + 15 + 15 + 16 + 16 + 18 + 18 + 20 + 20 + 23 + 25 + 25 = 243. There are 15 classes, so the mean class size is 243/15 ≈ 16.2.
For Seaside School, the median class size is the average of the 8th and 9th values when the data is sorted in ascending order. The 8th and 9th values are both 15, so the median class size is 15.
To find the mean class size for Seaside School, we can add up all the class sizes and divide by the total number of classes. The sum of the class sizes is 10 + 10 + 10 + 11 + 12 + 15 + 15 + 16 + 17 + 17Part A (continued):
18 + 18 + 20 + 20 + 25 = 222. There are 14 classes, so the mean class size is 222/14 ≈ 15.9.
Therefore, the measures of center for Bay Side School are: median = 25, mean ≈ 16.2.
The measures of center for Seaside School are: median = 15, mean ≈ 15.9.
Part B: To calculate the measures of variability, we can find the range and the interquartile range (IQR) for each school.
For Bay Side School, the range is the difference between the largest and smallest class sizes. The largest class size is 25, and the smallest class size is 12, so the range is 25 - 12 = 13.
To find the IQR for Bay Side School, we need to find the first quartile (Q1) and the third quartile (Q3) of the data. From the stem-and-leaf plot, we can see that Q1 is 15 and Q3 is 20. Therefore, the IQR is 20 - 15 = 5.
For Seaside School, the range is the difference between the largest and smallest class sizes. The largest class size is 25, and the smallest class size is 10, so the range is 25 - 10 = 15.
To find the IQRPart B (continued): for Seaside School, we need to find the first quartile (Q1) and the third quartile (Q3) of the data. From the stem-and-leaf plot, we can see that Q1 is 12 and Q3 is 18. Therefore, the IQR is 18 - 12 = 6.
Therefore, the measures of variability for Bay Side School are: range = 13, IQR = 5.
The measures of variability for Seaside School are: range = 15, IQR = 6.
Part C: If you are interested in a smaller class size, Seaside School is a better choice because its measures of center are lower than those of Bay Side School, indicating that its class sizes tend to be smaller on average. Additionally, Seaside School has a smaller range and IQR, indicating less variability in class size. Therefore, there is less chance of encountering very large classes at Seaside School compared to Bay Side School.