Are the whole numbers closed under division justify with example?
Answers
The division of the whole numbers is not closed under property as the division of whole number is not always a whole number.
A set has the closure property under a particular operation if the result of the operation is always an element in the set. If a set has the closure property under a particular operation then we say that the set is “closed under the operation.” The closure property of the division tells that the result of the division of two whole numbers is not always a whole number. Whole numbers are not closed under division that is a ÷ b is not always a whole number.
For example, 5 and 8 are whole numbers, but 5÷8 is not a whole number.
Therefore, closure property does not exist for division of whole numbers.
To learn more about Closed under property please visit:
https://brainly.com/question/29798485
#SPJ4
Related Questions
Is πxy=4 a linear equation?
Answers
Answer:
Yes
Step-by-step explanation:
It is a first-degree equation. Look at the exponents of each variable (x, y), they are not written because they are 1
Hope this helps
Evaluate 1/3 x 5/6.
A. 1/15
B. 6/15
C. 5/18
D. 3/30
Answers
Answer:
C
Step-by-step explanation:
1x5=5
3x6=18
and you can't simplify 5/18.
Answer:
5/18
Step-by-step explanation:
1 times 5 equals 5. 3 times 6 equals 18.
Find the arc length of the semicircle. Enter an exact answer in terms of . units

Answers
Answer:
The answer is 37.699111848 units or 0 units, pick
Step-by-step explanation:
2πr (θ/360)
find (a) a set of parametric equations and (b) if possible, a set of symmetric equations of the line passing through the point and parallel to the specified vector or line. (Write the direction numbers as integers.) Point (-2, 0, 3) Parallel to v = 2i + 4j - 2k
Answers
A set of symmetric equations for the line is: (x + 2)/1 = (y - 8)/2 = (z + 1)/(-2).
(a) To find a set of parametric equations, we need to find two points on the line. Since the line is parallel to the vector v = 2i + 4j - 2k, we can use this vector to find another point on the line. Let's call this point (x, y, z). Then we have:
(x + 2)/2 = (y - 0)/4 = (z - 3)/(-2)
Simplifying these equations, we get:
x + 2 = y/2
x + 2 = -z/2 + 3
Solving for x, y, and z, we get:
x = y/2 - 2
y = 2x + 4
z = -2x + 3
So a set of parametric equations for the line is:
x = t - 2
y = 2t + 4
z = -2t + 3
(b) To find a set of symmetric equations, we need to eliminate the parameter t from the parametric equations. We can do this by using the equations:
x = t - 2
y = 2t + 4
z = -2t + 3
Solving the first equation for t, we get:
t = x + 2
Substituting this into the other two equations, we get:
y = 2(x + 2) + 4 = 2x + 8
z = -2(x + 2) + 3 = -2x - 1
So a set of symmetric equations for the line is:
(x + 2)/1 = (y - 8)/2 = (z + 1)/(-2)
Note that these equations are not unique, as we could have chosen different points on the line to eliminate the parameter t. However, any set of symmetric equations for the line will have the same form as the equations above.
To learn more about parametric equations visit: https://brainly.com/question/28537985
#SPJ11
8 circles and 20 squares what is the simplest ratio of total shapes
Answers
Answer
8:28 Hope this helps.
It appears that over the past 50 years, the number of farms in the United States declined while the average size of farms increased. The following data provided by the U.S. Department of Agriculture show five-year interval data for U.S. farms. Use these data to develop the equation of a regression line to predict the average size of a farm (y) by the number of farms (x). Discuss the slope and y-intercept of the model.
Year Number of Farms (millions) Average Size (acres)
1960 5.67 209
1965 4.66 258
1970 3.99 302
1975 3.38 341
1980 2.92 370
1985 2.51 419
1990 2.45 427
1995 2.28 439
2000 2.16 457
2005 2.07 471
2010 2.18 437
2015 2.10 442
Answers
Regression line: The regression line can be given as follows: y= ax + b Where, x is the independent variable (Number of Farms) y is the dependent variable (Average Size) a is the slope of the line b is the y-intercept of the line The table for these variables is given below.
Slope: The slope of the regression line can be calculated as follows:(∆y / ∆x) = (y2 - y1) / (x2 - x1)Substituting the values of x1 = 5.67, y1 = 209, x2 = 2.10, and y2 = 442, we get:(∆y / ∆x) = (442 - 209) / (2.10 - 5.67)≈ 77.8Thus, the slope of the regression line is approximately 77.8. This means that the average size of farms increased by around 77.8 acres for every one million decline in the number of farms.
Y-intercept:The y-intercept of the regression line can be found by substituting the slope and any one set of values for x and y in the equation of the line. Using x = 5.67 and y = 209, we get:209 = (77.8) (5.67) + bb = 170.5
Thus, the y-intercept of the regression line is approximately 170.5. This means that if the number of farms were 0, the average size of farms would be around 170.5 acres.
To know more about regression visit:
https://brainly.com/question/32505018
#SPJ11
A Norman window has the shape of a rectangle surmounted by a semicircle. (Thus the diameter of the semicircle is equal to the width of the rectangle. See the figure below If the perimeter of the window is 24 ft, find the value of x so that the greatest possible amount of light is admitted
Answers
The perimeter equation is:
2x + x + (1/2)πx = 24 ft.
Simplifying the equation, we have:
(5/2)πx + 3x = 24 ft.
To find the value of x, we solve the equation:
(5/2)πx + 3x = 24 ft.
This equation can be solved numerically or algebraically to find the value of x.
The perimeter of a Norman window can be calculated by adding the lengths of all its sides. In this case, the perimeter is given as 24 ft.
Let's break down the components of the Norman window:
- The rectangular part has two equal sides and two equal widths. Let's call the width of the rectangle "x" ft.
- The semicircle on top has a diameter equal to the width of the rectangle, which is also "x" ft.
To find the perimeter, we need to consider the lengths of all sides of the rectangle and the semicircle.
The perimeter consists of:
- Two equal sides of the rectangle, each with a length of "x" ft. So, the total length for both sides of the rectangle is 2x ft.
- The width of the rectangle, which is also "x" ft.
- The curved part of the semicircle, which is half the circumference of a circle with a diameter of "x" ft. The formula for the circumference of a circle is C = πd, where C is the circumference and d is the diameter. So, the circumference of the semicircle is (1/2)πx ft.
To summarize, the perimeter equation is:
2x + x + (1/2)πx = 24 ft.
Simplifying the equation, we have:
(5/2)πx + 3x = 24 ft.
To find the value of x, we solve the equation:
(5/2)πx + 3x = 24 ft.
This equation can be solved numerically or algebraically to find the value of x.
Learn more about Equation here,https://brainly.com/question/29174899
#SPJ11
In simple graphical method a graph is plotted from the available data, between water usage and population. 2) Pressure in a distribution system must be high enough to permit the fire department adequate hydrant flows. 3) Distribution system is used to describe collectively the facilities used to supply water from its source to the point of usage. 4) Brackish water or briny water is water that has more salinity than fresh water, and more than seawater salinity. 5) The effect of monthly variation influences the design of storage reservoirs. 6) Jordan is not considered a "Water Scarce" country. 7) If a fire breaks out, a small quantity of water is required to be supplied during long duration, necessitating the need for a maximum rate of hourly supply. 8) The Manning equation is commonly used to design and evaluate the performance of sanitary sewers. 9) If d is less than 200 mm then the pipe final diameter D is 200 mm. 10) The diameter for lateral pipe is larger than the diameter of interceptor pipe.
Answers
The given statements are correct or incorrect is given below:
1) Correct.
2) Correct.
3) Correct.
4) Correct.
5) Correct.
6) Incorrect.
7) Correct.
8) Correct.
9) Correct.
10) Incorrect.
Here, we have,
1) Correct. In a simple graphical method, a graph is plotted to show the relationship between water usage and population.
2) Correct. The pressure in a distribution system needs to be sufficient to allow for adequate hydrant flows in case of a fire.
3) Correct. The term "distribution system" refers to the infrastructure and facilities used to supply water from its source to the point of usage.
4) Correct. Brackish water is water that has a higher salinity level than fresh water and even higher than seawater.
5) Correct. Monthly variation in water usage can impact the design and capacity requirements of storage reservoirs.
6) Incorrect. Jordan is considered a "Water Scarce" country, as it faces significant challenges in terms of water availability and scarcity.
7) Correct. During a fire, a significant quantity of water needs to be supplied over an extended period, necessitating a high rate of hourly supply.
8) Correct. The Manning equation is commonly used in the design and evaluation of sanitary sewers.
9) Correct. If the diameter (d) is less than 200 mm, the pipe's final diameter (D) is set at 200 mm.
10) Incorrect. The diameter of the interceptor pipe is typically larger than the diameter of the lateral pipe. The interceptor pipe carries wastewater from multiple lateral pipes.
To learn more on graph click:
brainly.com/question/17267403
#SPJ4
Factor each polynomial.
9x^2-25
Answers
Answer:
(3x + 5) (3x - 5)
Step-by-step explanation:
Please help me with this problem
Evaluate (-½·3)³
Answers
Answer: -27/8
Step-by-step explanation:
\(\left(-\frac{1}{2}\cdot \:3\right)^3\)
\(\mathrm{Apply\:exponent\:rule}:\quad \left(-a\right)^n=-a^n,\:\quad \mathrm{if\:}n\mathrm{\:is\:odd}\)
\(\left(-\frac{1}{2}\cdot \:3\right)^3=-\left(\frac{1}{2}\cdot \:3\right)^3\)
\(=-\left(\frac{1}{2}\cdot \:3\right)^3\)
\(\mathrm{Apply\:exponent\:rule}:\quad \left(a\cdot \:b\right)^n=a^nb^n\)
\(\left(\frac{1}{2}\cdot \:3\right)^3=\left(\frac{1}{2}\right)^3\cdot \:3^3\)
\(=-\left(\frac{1}{2}\right)^3\cdot \:3^3\)
\(=-\frac{1}{8}\cdot \:3^3\)
\(=-\frac{1}{8}\cdot \:27\)
\(=-\frac{27}{8}\)
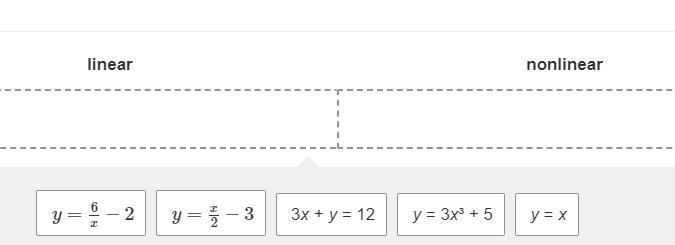
Determine if each function is linear or nonlinear. Drag each function into a box to correctly classify it.
Answers
y= x/2 -3 , y+3x = 12 and y = x are determined as linear equations , while y=6/x -2 and y= 3x^3 +5 are non-linear equations.
What do you mean by linear equations?A linear equation is a mathematical equation that forms a constant straight line on a graph.
What exactly is a nonlinear equation?Non-linear equations are functional equations that form different types of curves or other non-linear shapes on a graph.
According to the slope-intercept formula of the straight line : y=mx+b
1. y=6/x - 2 ,is not satisfying the above formula of straight line , having x in the denominator, hence it is a non-linear equation.
2. y=x/2-3 , here slope(m)=1/2 and intercept(b)=-3 which are real numbers and satisfy the straight line formula , hence it is a linear equation.
3. y=-3x+12, here slope(m)=-3 and intercept(b)=12 as real numbers and satisfy the straight line graph formula , hence it is a linear equation.
4. y = 3x^3+5, here slope(m)=3x^2 which is not a real number, hence not satisfying the given formula it is a non-linear equation.
5. y = x , here slope(m)=1 and intercept(b) =0 which are real numbers and satisfy the straight line graph formula ,hence it is a linear equation.
To learn more about linear and non-linear equations visit to the given link
https://brainly.com/question/20054300
#SPJ1
Please solve this equation

Answers
Answer: Below
Step-by-step explanation:
Well they already gave you crucial information. The radius, or r, is 19, and pi can be substituted with 3. Using that we can do:
C = 2 * 3 * 19
C = 6 * 19
C = 114
Our answer is 114.
compare 1/4 and 2/9 by converting each fraction to a decimal
Answers
When comparing the fractions 1/4 and 2/9 by converting them to decimals, we find that 1/4 is equal to 0.25 and 2/9 is equal to 0.2222 (repeating).
To convert a fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number). Let's start with 1/4. When we divide 1 by 4, we get 0.25. Therefore, 1/4 is equal to 0.25 as a decimal.
Now let's convert 2/9 to a decimal. When we divide 2 by 9, we get 0.2222 (repeating). This means that the decimal representation of 2/9 is 0.2222, where the digit 2 repeats indefinitely.
Comparing these two decimals, we can see that 0.25 is larger than 0.2222. Therefore, 1/4 is greater than 2/9 when comparing them as decimals.
In summary, 1/4 is equal to 0.25 as a decimal, while 2/9 is equal to 0.2222 (repeating). Comparing the decimals, we find that 1/4 is greater than 2/9.
For more questions on fractions
https://brainly.com/question/78672
#SPJ8
(4x-1)(3x^2+3x-5) (4x−1)(3x 2 +3x−5)
Answers
Hi.
Answer:
\(\left(4x-1\right)^2\left(3x^2+3x-5\right)^2\)
Step-by-step explanation:
\((aa=a^2) \left(4x-1\right)\left(4x-1\right)=\left(4x-1\right)^2\\=\left(4x-1\right)^2\left(3x^2+3x-5\right)\left(3x^2+3x-5\right)\\\left(3x^2+3x-5\right)\left(3x^2+3x-5\right)=\left(3x^2+3x-5\right)^2\\=\left(4x-1\right)^2\left(3x^2+3x-5\right)^2\)
If a numser has an even exponent can it ever be negative when it is simplified?
Explain.
Answers
Answer: No, it can never be negative.
==================================================
Explanation:
Consider the expression x^2
If x were some negative number, say x = -3, then
x^2 = (-3)^2 = 9 which is a positive result.
Picking any negative number for x will make x^2 positive.
We can think of it like this
(-3)^2 = (-3)*(-3) = 9
The two negatives multiply to a positive.
This also happens with exponents 4,6,8, etc. Any even exponent will have an even number of negative signs, all of which cancel out.
Triangle JKL is isosceles. The measure of angle J is 72 degrees and the measure
of angle K is 36 degrees.

Answers
Step-by-step explanation:
"which is the measure of angle L?"
the total angle measures of all angles on a triangle should always equal 180
72 + 36 = 108
180 - 108 = 72!
angle L is 72 degrees!
"which angle is the vertex angle?"
from my understanding, the angle opposite the base would be the vertex angle
since j and k are equal, we can only assume 36 is the vertex angle!
hope this helps! if so, pls give brainliest!
Answer:
hi. I'm so sorry I just need to answer some questions. I'm sorry
Un cazador se encuentra en la parte mas alta de un arbol. Para averiguar a que altura se encuentra, deja caer una bola, observando que demora 4 segundos. Encuentra el alto del arbol (g=10m/s2)
Answers
Answer:
80 m
Step-by-step explanation:
La velocidad inicial de la pelota es 0 m/s.
La altura del árbol es s.
El tiempo necesario es de 4 segundos.
Podemos aplicar una de las ecuaciones de movimiento de Newton:
\(s = ut + \frac{1}{2}gt^2\)
donde u = velocidad inicial
t = tiempo empleado
g = aceleración debido a la gravedad
Por lo tanto:
\(s = 0 * 4 + (1/2 * 10 * 4^2)\\\\s = 0 + 80 \\\\s = 80 m\)
El árbol tiene 80 metros de altura.
0.6,P(B)=0.5, and P(A∩B)=0.15 (a) Compute the probability that the selected individual has at least one of the two types of cards (i.e., the probability of the event A∪B. x (b) What is the probability that the selected individual has neither type of card? x (c) Describe, in terms of A and B, the event that the selected student has a Visa card but not a MasterCard. A ′
∩B ′
A ′
∩B A∪B ′
A∩B ′
A ′
∪B ′
Calculate the probability of this event.
Answers
(a) The probability that the selected individual has at least one of the two types of cards is 0.95 or 95%.
(b) The probability that the selected individual has neither type of card is 0.05 or 5%.
(c) The probability that the selected student has a Visa card but not a MasterCard is 0.25 or 25%.
To solve this problem, we'll use the following notation:
- P(A) represents the probability of event A.
- P(B) represents the probability of event B.
- P(A∩B) represents the probability of the intersection of events A and B.
(a) To compute the probability that the selected individual has at least one of the two types of cards (A∪B), we can use the formula for the union of two events:
P(A∪B) = P(A) + P(B) - P(A∩B)
Given that P(A) = 0.6, P(B) = 0.5, and P(A∩B) = 0.15, we can substitute these values into the formula:
P(A∪B) = 0.6 + 0.5 - 0.15 = 0.95
Therefore, the probability that the selected individual has at least one of the two types of cards is 0.95 or 95%.
(b) To find the probability that the selected individual has neither type of card, we can use the complement rule. The complement of having either type of card is the event of having neither type of card, denoted as (A∪B)'.
P((A∪B)') = 1 - P(A∪B)
We already calculated P(A∪B) to be 0.95, so we can substitute that value into the formula:
P((A∪B)') = 1 - 0.95 = 0.05
Therefore, the probability that the selected individual has neither type of card is 0.05 or 5%.
(c) The event that the selected student has a Visa card but not a MasterCard can be represented as A'∩B', where A' represents the complement of event A (not having a Visa card) and B' represents the complement of event B (not having a MasterCard).
P(A'∩B') can be calculated as follows:
P(A'∩B') = P(A') - P(A'∩B)
To calculate P(A'), we subtract P(A) from 1:
P(A') = 1 - P(A) = 1 - 0.6 = 0.4
Given that P(A∩B) = 0.15, we can substitute the values into the formula:
P(A'∩B') = 0.4 - 0.15 = 0.25
Therefore, the probability that the selected student has a Visa card but not a MasterCard is 0.25 or 25%.
Learn more about complement of event here:
https://brainly.com/question/23528544
#SPJ11
9. Rewrite in order from least to greatest. 13%, 16/100 01/5, 0.15, 1/10
Answers
Answer:
1/10, 13%, 0.15, 16/100, 1/5
Step-by-step explanation:
Given the following question:
13%, 16/100, 1/5, 0.15, and 1/10
In order to find the answer to this question we can rewrite all the following fractions/percent into decimals and then compare.
\(\frac{16}{100} =16\div100=0.16\)
\(\frac{1}{5} =1\div5=0.2\)
\(\frac{1}{10} =1\div10=0.1\)
\(13=0.13\)
0.13, 0.16, 0.15, 0.2, and 0.1
0.1, 0.13, 0.15, 0.16, 0.2
1/10, 13%, 0.15, 16/100, 1/5
Hope this helps.
Mrs. Newby made strawberry jam and raspberry jam. She made enough strawberry jam to fill ( 1)/(6) of a jar. If she made 4( 1)/(3) times as much raspberry jam as strawberry jam, how many jars will the raspberry jam fill?
Answers
The number of jars that the raspberry jam fills is given as follows:
13/18 of a jar.
How to obtain the number of jars?The number of jars that the raspberry jam fills is obtained applying the proportions in the context of the problem.
The fraction that relates the ratio between the two amounts is given as follows:
4 and 1/3 = 4 + 1/3 = 12/3 + 1/3 = 13/3.
Hence the number of jars that the raspberry jam fills is given as follows:
13/3 x 1/6 = 13/18 of a jar.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ4
errors that pertain to anything in the research process except sample size are known as: a. intentional field work error. b. non-sampling error. c. field error. d. sampling error.]
Answers
Errors that pertain to anything in the research process except sample size are known as option b. non-sampling error.
Non-sampling errors are errors that occur in the research process other than those related to sample size. These errors can arise at any stage of the research process, including data collection, data processing, analysis, and interpretation. Examples of non-sampling errors include errors in data entry or coding, selection bias, measurement bias, interviewer bias, and response bias. Non-sampling errors can have a significant impact on the accuracy and validity of research findings and should be carefully controlled and minimized to the extent possible.
To know more about sample size,
https://brainly.com/question/25894237
#SPJ11
student : teacher ratio at a school is 15: 1.
(i) How many students are there if there is a total of 320 students and staff?
(ii) What would be the new student: teacher ratio if two more teachers joined the school?
Answers
Answer:
300 students and 150 : 11
Step-by-step explanation:
(i)
sum the parts of the ratio , 15 + 1 = 16 parts
divide the total students/staff by 16 to find the value of one part of the ratio.
320 ÷ 16 = 20 , then
number of students = 15 × 20 = 300
(ii)
number of staff = 320 - 300 = 20
if 2 more teachers join the school then there is a total of 22 staff
student : teacher = 300 : 22 = 150 : 11
A project that provides annual cash flows of $2,200 for nine years costs $9,100 today.
At a required return of 9 percent, what is the NPV of the project?
At a required return of 25 percent, what is the NPV of the project?
At what discount rate would you be indifferent between accepting the project and rejecting it?
Answers
We can solve for r using numerical methods or trial and error. One possible way is to use Excel's goal seek function, which gives us a discount rate of approximately 16.5%. Therefore, at a discount rate of 16.5%, the NPV of the project is zero, and we would be indifferent between accepting the project and rejecting it.
Using the formula for NPV, we have:
\(NPV = -Cost + (CF1 / (1+r)^1) + (CF2 / (1+r)^2) + ... + (CFn / (1+r)^n)\)
where CF is the annual cash flow, r is the required rate of return, and n is the number of years.
Plugging in the given values, we get:
At a required return of 9%:
\(NPV = -9100 + (2200 / (1+0.09)^1) + (2200 / (1+0.09)^2) + ... + (2200 / (1+0.09)^9)\\NPV = -9100 + 1704.13 + 1562.30 + ... + 653.89\\NPV = $404.19\)
At a required return of 25%:
NPV = -9100 + (2200 / (1+0.25)^1) + (2200 / (1+0.25)^2) + ... + (2200 / (1+0.25)^9)
\(NPV = -9100 + 1548.28 + 1179.08 + ... + 160.69\\NPV = -$1,489.91\)
To find the discount rate at which we would be indifferent between accepting the project and rejecting it, we can use the NPV formula and set it equal to zero:
\(0 = -9100 + (2200 / (1+r)^1) + (2200 / (1+r)^2) + ... + (2200 / (1+r)^9)\)
To know more about discount rate here
https://brainly.com/question/9841818
#SPJ4
2. At West School, there are 20 classrooms.
Each classroom has 20 students. How
many students are at West School?
Answers
Answer:
Step-by-step explanation:
20x20=400
Answer: Your answer is 400 students, hope this helps.
When the two roots of the characteristic equation are both equal to r, the general solution to the corresponding second order linear homogeneous ODE with constant coefficients is of the form (at+b)âe^rt
Answers
y = (At + B) e^(rt)
where A = -r/2 and B = 3r/2, as expected.
When the two roots of the characteristic equation are both equal to r, we say that the roots are equal or repeated. In this case, the general solution to the corresponding second order linear homogeneous ODE with constant coefficients is of the form:
y = (At + B) e^(rt)
where A and B are constants to be determined by the initial or boundary conditions.
However, the form given in the question, (at+b)âe^rt, is not correct. The â symbol is not standard notation for mathematical expressions and its meaning is unclear. It is possible that it was intended to represent a coefficient or parameter, but without more information, we cannot determine its value or significance.
To see why the correct form of the solution is y = (At + B) e^(rt), we can use the method of undetermined coefficients. Suppose that y = e^(rt) is a solution to the homogeneous ODE with repeated roots. Then, we can try the solution y = (At + B) e^(rt) and see if it satisfies the ODE.
Taking the first and second derivatives of y, we get:
y' = A e^(rt) + r(At + B) e^(rt) = (Ar + r(At + B)) e^(rt)
y'' = A r e^(rt) + r^2(At + B) e^(rt) = (Ar^2 + 2rAt + r^2B) e^(rt)
Substituting y, y', and y'' into the homogeneous ODE with repeated roots, we get:
(Ar^2 + 2rAt + r^2B) e^(rt) = 0
Since e^(rt) is never zero, we can divide both sides by e^(rt) to get:
Ar^2 + 2rAt + r^2B = 0
This is a linear equation in A and B, and we can solve for them by using the initial or boundary conditions. For example, if we are given that y(0) = 1 and y'(0) = 0, we have:
y(0) = A e^(0) + B e^(0) = A + B = 1
y'(0) = (Ar + rB) e^(0) + A e^(0) = Ar + A = 0
Solving this system of equations, we get:
A = -r/2, B = 3r/2
Therefore, the general solution to the homogeneous ODE with repeated roots is:
y = (-rt/2 + 3r/2) e^(rt)
which can be rewritten as:
y = (At + B) e^(rt)
where A = -r/2 and B = 3r/2, as expected.
To learn more about roots visit:
https://brainly.com/question/29755184
#SPJ11
how much variance between two variables has been explained by a correlation of .9?
Answers
A correlation of .9 indicates that 81% of the variance between two variables has been explained.
Correlation measures the strength of the relationship between two variables. A perfect positive correlation is 1.0, indicating that the two variables move in the same direction together. A perfect negative correlation is -1.0, indicating that the two variables move in opposite directions. A correlation of 0 indicates no relationship between the two variables.
To determine the proportion of variance explained by a correlation, you need to square the correlation coefficient (in this case, 0.9). This is called the coefficient of determination (R^2). So, you calculate:
R^2 = (0.9)^2 = 0.81
Thus, a correlation of 0.9 explains 81% of the variance between the two variables.
To know more about variables visit:
https://brainly.com/question/29583350
#SPJ11
Can I drink some nice internet juice
Answers
Answer: Um sure you can
Solve for x. Your answer must be simplified. -3 < x/-4
Answers
Answer:
x<12
Step-by-step explanation:
Let's solve your inequality step-by-step.
−3< x/ −4
Step 1: Simplify both sides of the inequality.
−3< −1/ 4 x
Step 2: Flip the equation.
−1/ 4 x>−3
Step 3: Multiply both sides by 4/(-1).
( 4/ −1 )*( −1/ 4 x)>( 4 /−1 )*(−3)
x<12
Answer:
x<12
Anyone who know,s this please help?

Answers
Do you have to add both of the bases in a triangular prism to find the volume? Someone please help!
Answers
Answer:
Yes,you have to add both of the bases in a triangle prism to find the volume.
Step-by-step explanation:
took the test.
Answer:
No, you need it onceStep-by-step explanation:
Volume of the prism:
V = bhYou use the area of the base once, multiply it by the height to find the volume
The answer is no.