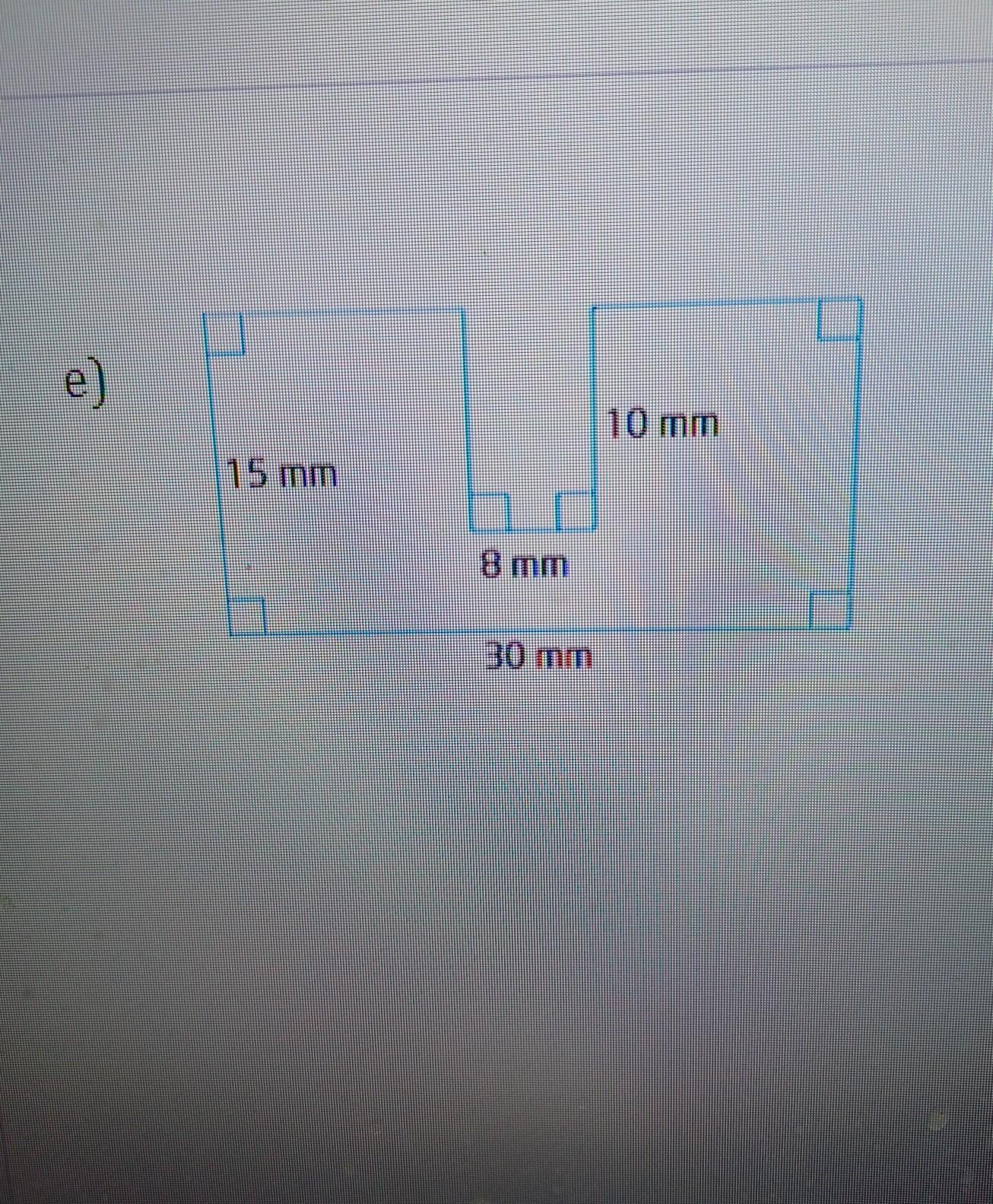
Answers
Answer:
37cm(370mm)
Step-by-step explanation:
(15×30)-(8×10)
450-80
370
Related Questions
I really need help understanding proofs. Anyone please explain within a few mins or so?
Answers
Answer:
so where is your question..I'm good in proving
Solve 2x - 11 = k for x.
Answers
Reorder the terms:
-11 + 2x = k
Solving
-11 + 2x = k
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '11' to each side of the equation.
-11 + 11 + 2x = 11 + k
Combine like terms: -11 + 11 = 0
0 + 2x = 11 + k
2x = 11 + k
Divide each side by '2'.
x = 5.5 + 0.5k
Simplifying
A market research company wishes to know how many energy drinks teenagers drink each week. They want to construct a 80% confidence interval with an error of no more than 0.08. A consultant has informed them that a previous study found the mean to be 7.3 energy drinks per week and found the standard deviation to be 0.7. What is the minimum sample size required to create the specified confidence interval
Answers
Answer: 126 samples
Step-by-step explanation:
Given that :
Standard deviation (σ) = 0.7
Mean (m) = 7.3
Error (E) = 0.08
α = 80%
The sample size n can be obtained using the relation :
n = [(Zcrit * standard deviation) / Error]^2
The Zcritical at 80% = 1.282
Hence,
n = ((1.282 * 0.7) / 0.08)^2
n = (0.8974 / 0.08)^2
n = 11.2175^2
n = 125.83230625
n = 126
Harry and his sister Jess have some money in the ratio Harry : Jess = 1:4
Harry has £7.35
They pay £16.99 for a present for a friend.
Harry uses
3/4 of his money.
Jess pays the rest.
How much money does Jess have left?

Answers
Answer:
£17.92
Step-by-step explanation:
Harry : Jess
1 : 4
£7.35 : £29.40
(for every 1 Harry has, Jess has 4, so Jess = 4 x 7.35 = 29.40)
PRESENT:
Harry uses 3/4 of his money = 0.75 x 7.35 = £5.51
So Jess pays: 16.99 - 5.51 = £11.48
Jess has left: 29.40 - 11.48 = £17.92
The equation Y= X^2/2 - 8 and Y= 2X -2 are graphed below what are the solutions to the equation X^2/2 - 8 = 2X -2 
Answers
The equation X^2/2 - 8 = 2X - 2 has two solutions, X = 6 and X = -2. These are the values of X that satisfy the equation and make both equations Y = X^2/2 - 8 and Y = 2X - 2 intersect on the graph.
To find the solutions to the equation X^2/2 - 8 = 2X - 2, we need to set the two equations equal to each other and solve for X.
The equation is:
X^2/2 - 8 = 2X - 2
To simplify the equation, let's multiply both sides by 2 to eliminate the fraction:
X^2 - 16 = 4X - 4
Next, we rearrange the equation to have all terms on one side:
X^2 - 4X - 12 = 0
Now, we can solve this quadratic equation by factoring, completing the square, or using the quadratic formula. Let's use factoring in this case:
(X - 6)(X + 2) = 0
Setting each factor equal to zero gives us two possible solutions:
X - 6 = 0 --> X = 6
X + 2 = 0 --> X = -2
So the solutions to the equation X^2/2 - 8 = 2X - 2 are X = 6 and X = -2.
For more such question on intersect . visit :
https://brainly.com/question/30915785
#SPJ8
2x+7x=77
5x+7y=115
solve for x & y that makes both expressions true.
Answers
The solution that makes both expressions true is x = 8.55556 and y = 10.31746.
To solve for x and y, we need to use a system of equations involves finding the values of x and y that satisfy both equations simultaneously.
We can start by using the first equation to solve for x:
2x + 7x = 77
Combining like terms:
9x = 77
Dividing both sides by 9:
x = 8.55556 (rounded to six decimal places)
Now that we know the value of x we can use either equation to solve for y. Let's use the second equation:
5x + 7y = 115
Substituting x = 8.55556:
5(8.55556) + 7y = 115
Simplifying:
42.7778 + 7y = 115
Subtracting 42.7778 from both sides:
7y = 72.2222
Dividing both sides by 7:
y = 10.31746 (rounded to six decimal places)
For similar questions on expressions
https://brainly.com/question/1859113
#SPJ11
What is the volume of a rectangular prism with the following dimensions (5 in x 8 in x 11 in)
Answers
solve the system with elimination 4x+3y=1 -3x-6y=3
Answers
Answer:
x = 1, y = -1
Step-by-step explanation:
If we have the two equations:
\(4x+3y=1\) and \(-3x - 6y = 3\), we can look at which variable will be easiest to eliminate.
\(y\) looks like it might be easy to get rid of, we just have to multiply \(4x+3y=1\) by 2 and y is gone (as -6y + 6y = 0).
So let's multiply the equation \(4x+3y=1\) by 2.
\(2(4x + 3y = 1)\\8x + 6y = 2\)
Now we can add these equations
\(8x + 6y = 2\\-3x-6y=3\\\)
------------------------
\(5x = 5\)
Dividing both sides by 5, we get \(x = 1\).
Now we can substitute x into an equation to find y.
\(4(1) + 3y = 1\\4 + 3y = 1\\3y = -3\\y = -1\)
Hope this helped!
A shopper pays $49.05 for a $45 desk chair after sales tax is added. What is the sales tax percentage?
Answers
PLEASE HELP!!!
There are many different kinds of numbers (whole numbers, fractions, etc.). Name some different types of numbers. Do you know how to do operations with different types of numbers? What operations do you know how to perform with the different types of numbers?
Answers
Answer:
Types of numbers
Natural Numbers - Common counting numbers.
Prime Number - A natural number greater than 1 which has only 1 and itself as factors.
Composite Number - A natural number greater than 1 which has more factors than 1 and itself.
Whole Numbers - The set of Natural Numbers with the number 0 adjoined.
Integers - Whole Numbers with their opposites (negative numbers) adjoined.
Rational Numbers - All numbers which can be written as fractions.
Irrational Numbers - All numbers which cannot be written as fractions.
Real Numbers - The set of Rational Numbers with the set of Irrational Numbers adjoined.
Complex Number - A number which can be written in the form a + bi where a and b are real numbers and i is the square root of -1.
Step-by-step explanation:
Four out of 32 students in Mr. Lee’s class speak 3 languages. Which decimal represents the number of students who speak 3 languages?
Answers
Answer:
.125
Step-by-step explanation:
4 is one-eighth (1/8) of 32, which would be represented by the decimal .125 or 0.125
help me find the slope please
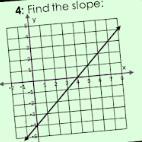
Answers
Answer:
3/4
Step-by-step explanation:
Ok, so I see that the x-intercept is (4,0), while the y-intercept is(-3,0)
Slope is rise/run
Between these two points, the line rose 3 and horizontally went 4 units to the right. Therefore, the slope is 3/4.
Feel free to tell me if I did anything wrong! :)
Also, if you're still confused, I could explain it another way.
ATTEMPT 3 OF TRYING TO GET THIS ANSWERED PLEASE HELP
In this diagram, x || y || z and m<9 = 93°.
What is the measure of each angle?
Drag and drop the correct measurements by the arrows to
match each angle.
m<2 ——>
m<4——->
m<7——->
87° 89° 91° 93 °

Answers
Answer:
m<2 = 87
m<4 = 87
m<7 = 93
Step-by-step explanation:

Question 3 (1 point)
Karl wants to find the width RQ of a river. He starts at point R, and walks
perpendicular along the edge of the river 42 ft and marks point S. He then walks 28
ft further and marks point T. He turns 90° and walks until his location (point U), point
S, and point Q are collinear. Suppose TU= 68 ft. What is the width of the river in
feet?
Answers
The width RQ of the river is approximately 61.98 ft.
To find the width RQ of the river, we can use the properties of perpendicular lines and collinearity.
Given that Karl starts at point R and walks perpendicular along the edge of the river 42 ft to point S, we can draw a line segment RS of length 42 ft.
From point S, Karl walks 28 ft further to point T. We can draw another line segment ST of length 28 ft.
Now, Karl turns 90° from point T and walks until his location (point U), point S, and point Q are collinear. Let's denote the length of this line segment as UQ.
From the given information, we know that TU = 68 ft.
Since U, S, and Q are collinear, we can form a right triangle by connecting UQ and US.
The length of UQ can be found using the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In this case, we have:
UQ² = TU² - US²
UQ² = 68² - 28²
UQ² = 4624 - 784
UQ² = 3840
Taking the square root of both sides, we have:
UQ = √3840
UQ ≈ 61.98 ft
Therefore, the width RQ of the river is approximately 61.98 ft.
Note: It's important to keep in mind that this solution assumes the river is a straight line and that Karl's path is perpendicular to the river's edge. In reality, the river's edge may not be perfectly straight, and the path Karl walks may not be exactly perpendicular.
For more such questions on width visit:
https://brainly.com/question/25292087
#SPJ8
A local department store sells carpet in 4 sizes. Each carpet comes in 3 different qualities. One of the sizes comes in 5 colors. The other sizes come in 2 colors. How many choices of carpet are there
Answers
Answer:
23.
Step-by-step explanation:
You would multiply the 4 sizes of carpet by the 3 qualities, which equals 12. Then, you add 5+2+2+2. So it would end up being 12+11.
what is 25 divided by 1 1/4
Answers
Answer:
20
Step-by-step explanation:
25 ÷ 1.25 = 20
-5x-13, For x<-7
H(x)={3, For -7<_ x< 3
x+2, For x_> 3
Solve for
H(-7)
H(-2)
H(3)
H(9)
Thank you
Answers
The values of H(-7)=3, H(-2)=3, H(3)=5, H(9)=11 using the given equations by substituting the values.
What is equation?The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two expressions 3x + 5 and 14, which are separated by the 'equal' sign. A mathematical statement known as an equation is made up of two expressions joined together by the equal sign. a formula that expresses the connection between two expressions on either side of a sign. Typically, it has a single variable and an equal sign.
Here,
H(x)= {-5x-13 for x<-7
3 for -7<=x< 3
x+2 for x=> 3}
when x=-7,
H(x)=3
when x=-2,
H(x)=3
when x=3,
H(x)=x+2
H(x)=5
when x=9,
H(x)=x+2
H(x)=11
H(-7)=3, H(-2)=3, H(3)=5, H(9)=11 when the values are substituted under the conditions stated for the given equation.
To know more about equation,
https://brainly.com/question/10413253?referrer=searchResults
#SPJ1
Help help help please

Answers
Answer:
D=360_180÷9
D=360_20
D=340
Find the range and kernel (those are new words for the column space and nullspace) of T. (a) T(v₁, v₂) = (v₂, v₁). (b) T(v₁, v₂, v₃) = (v₁, v₂). (c) T(v₁, v₂) = (0, 0). (d) T(v₁, v₂) = (v₁, v₁).
Answers
In linear algebra, the kernel of a linear transformation is the set of all vectors that map to the zero vector in the codomain. It is also known as the null space of the transformation.
(a) Range: The range of T is the set of all possible outputs of T, which is the set of all 2-dimensional vectors where the first and second components can be any real number. Therefore, the range of T is R².
Kernel: The kernel of T is the set of all vectors in the domain of T that get mapped to the zero vector in the codomain. In this case, T(v₁, v₂) = (v₂, v₁) = (0, 0) if and only if v₁ = v₂ = 0. Therefore, the kernel of T is {(0, 0)}.
(b) Range: The range of T is the set of all possible outputs of T, which is the set of all 2-dimensional vectors where the third component is zero. Therefore, the range of T is the x-y plane in R³.
Kernel: The kernel of T is the set of all vectors in the domain of T that get mapped to the zero vector in the codomain. In this case, T(v₁, v₂, v₃) = (v₁, v₂) = (0, 0) if and only if v₁ = v₂ = 0. Therefore, the kernel of T is the set of all vectors of the form (0, 0, v₃), where v₃ can be any real number.
(c) Range: The range of T is the set of all possible outputs of T, which is the singleton set {(0, 0)}.
Kernel: The kernel of T is the set of all vectors in the domain of T that get mapped to the zero vector in the codomain. In this case, T(v₁, v₂) = (0, 0) if and only if v₁ and v₂ are arbitrary real numbers. Therefore, the kernel of T is the entire plane in R².
(d) Range: The range of T is the set of all possible outputs of T, which is the set of all 2-dimensional vectors where the second component is the same as the first component. Therefore, the range of T is the line in R² that passes through the origin and has slope 1.
Kernel: The kernel of T is the set of all vectors in the domain of T that get mapped to the zero vector in the codomain. In this case, T(v₁, v₂) = (v₁, v₁) = (0, 0) if and only if v₁ = 0. Therefore, the kernel of T is the y-axis in R².
To learn more about range visit;
https://brainly.com/question/28135761
#SPJ4
The graphed line can be expressed by which equation?
1. y+2=2/3(x×2)
2. y-2=3/4(x-1)
3. y-1=-3/4(x-2)
4. y-2=3/4(x-2)

Answers
The function f(x) = 2x^3 + 3x^2 is:
(a) even
(b) odd
(c) neither
(d) even and odd
Answers
d). Even and odd
Explanation:
2x^3 = even
Since any number times 2 will be even
3x^2 = even/odd
Let’s assume x = 2
Then 3(2)^2 = 3 x 4 = 12 = even
Assume x = 3
3(3)^2 = 3 x 9 = 27 = odd
Now we know our equation has:
even + even/odd = even and odd
Ex: 2 + 2 = 4 = even
Ex: 2 + 3 = 5 = odd
So our equation can be equal to either even and odd
Answer:
neither
Step-by-step explanation:
First we must determine if both x and -x are in the domain of the function
since it is a polynomial function our first condition is satisfied
Then we should calculate the image of -x :
2x(-x)^3 + 3*(-x)² = -2x^3+3x²
it is not equal to f(x) nor -f(x)
A tennis ball can in the shape of a right circular cylinder holds three tennis balls snugly. If the radius of a tennis ball is
3.5 cm, what percentage of the can is not occupied by tennis balls?
The percentage of the can that is not occupied by tennis balls is______%.
(Type an integer, fraction, or mixed number.)
Answers
The percentage of the can that is not occupied by tennis balls is approximately 80.14%.
We have,
The volume of the can = The volume of the cylinder - The volume of the three tennis balls.
The volume of the cylinder.
V(cylinder) = πr²h
where r is the radius and h is the height of the cylinder.
Since the can holds three tennis balls snugly, the height of the cylinder is equal to three times the diameter of a tennis ball.
= 3 × 2(3.5 cm)
= 21 cm.
V(cylinder)
= π (3.5 cm)² (21 cm)
= 2709.38 cm³
The volume of one tennis ball.
V (ball) = (4/3)πr³
where r is the radius of the tennis ball. Thus,
V(ball) = (4/3)π(3.5 cm)³ = 179.594 cm³
The total volume of the three tennis balls is:
V(3balls) = 3 V(ball)
= 3(4/3) π (3.5 cm)³
= 538.782 cm³
The volume of the can not be occupied by tennis balls.
V(not occupied) = V(cylinder) - V(3 balls)
= 2709.38 - 538.782
= 2170.598 cm³
The percentage of the can that is not occupied by tennis balls.
percentage = (V(not occupied / V(cylinder)) × 100%
= (2170.598 cm^3/2709.38 cm^3) × 100%
= 80.14%
Therefore,
The percentage of the can that is not occupied by tennis balls is approximately 80.14%.
Learn more about percentages here:
https://brainly.com/question/11403063
#SPJ1
Express the set x > 4 using interval notation.
Answers
Answer:
notation is the number 4
What inequality is represented by the number line graph?

Answers
Answer:
D. x ≤ 5
Step-by-step explanation:
The closed circle means greater than or equal to (≤) or less than or equal to (≥). The open circle is greater than (<) or less than (>).
And since the circle is closed and the arrow is going to the right, than x is either greater than 5 or equal to 5
Joe ran 12 laps around the field to run a total of 1 km on Sunday. How many laps will he need to run on Monday to run 4/6 of a km?
Answers
Answer:
\(4 \div 6 \times 12 = 4 \times 2 \\ \\ 4 \times 2 = 8\)
so, 8 laps
please mark it brainliest
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
10. A pipe whose diameter measures 1 1/4 inches should have less threads per inch than a pipe with a diameter of _______ inch.
A. 3
B. 1/2
C. 1
D. 11/2
Answers
A pipe whose diameter measures 1 1/4 inches should have less threads per inch than a pipe with a diameter of 11/2 inch. So, the correct answer is (D).
To determine the correct answer, we need to compare the diameters of the two pipes and understand the relationship between pipe diameter and threads per inch.
The number of threads per inch generally decreases as the pipe diameter increases. This means that a larger pipe diameter will have fewer threads per inch compared to a smaller pipe diameter.
Given that the first pipe has a diameter of 1 1/4 inches, we need to find the pipe diameter from the options that is larger than 1 1/4 inches.
The option that meets this requirement is D. 11/2. This represents a pipe diameter of 1 1/2 inches. Therefore, a pipe with a diameter of 1 1/2 inches should have fewer threads per inch than a pipe with a diameter of 1 1/4 inches. Therefore, the correct answer is D. 11/2.
For more questions on: diameter
https://brainly.com/question/30460318
#SPJ8
What's 10+10-5+10+5
Answers
Answer:
the answer is 30
Step-by-step explanation:
10+10=20-5=15+10=25+5=30
Answer:
30!
Step-by-step explanation:
1 Suppose the equation 28 = x. 4 in the Example is written in the form 4x = 28.
Is 7 still a solution? Explain.
Answers
Answer: yes
Step-by-step explanation:
if u substitute 7 into the x for 4x - 28 then it would be the same as 4(7), because any variable next to a number means multiplication.
hope this was an easier way for u to understand
Answer:
Yes, 7 is still a solution.
Step-by-step explanation:

(Geometry/shapes) Hi, can any expert guide me in solving this problem? or someone who knows this?
Trapezoid and Kites. (picture below)

Answers
69
Step-by-step explanation:
angles 111 and 3 are the same. in a trapezoid bottom base angles are the same and the top base angles are the same. so in order to find angle 2 you must subtract 111 from 180 because the top angles are supplementary to the bottom
180 - 111 = 69
Answer:
The answer will be 69
This is because angle 3 would also be 111
Angles in a quadrilateral add up to 360
So, 360-(111+111)
=138
there are two angles left, angle 1 ND 2, THEY ARE THE SAME VALUE. So DIVIDE 138 by 2, and you would get your answer 69 degrees.
Hope this helps!!