ASAP!!! LOOK AT THE IMAGE FOR THE GRAPH AND ANSWER CHOICES!! PLEASE HELP URGENT!!

Answers
Answer:
The answer is D.
4x + y = 2
x - y = 3
____________
When given a graph with an intersection of two lines, first locate the y-intercept (the point where x = 0) of each line, and then find it's slope by evaluating its change in y over the change in x.
It is also possible to eliminate the incorrect systems using substitution when given a point of intersection.
For example, as the point of intersection is apparent on this graph, you can substitute these coordinates from the graph into each of the systems of equations given in the choice answers to verify it.
For it to be a solution, it must satisfy (make true) both equations of the system.
(a, b) : (x, y)
Given that (1,-2) is our point of intersection according to the graph.
Choice A is incorrect because (1, -2) → x + 4y = 3 → (1) + 4(-2) = 3 → 1 + (-8) = 3 →
1 - 8 = 3 → -7 ≠ 3.
And (1, -2) → x + y = 2 → (1) + (-2) = 2 →
-1 ≠ 2.
It is already incorrect as one of the
equations in this system do not satisfy the coordinate.
Choice B is also incorrect because
(1, -2) → x + 4y = 2 → (1) + 4(-2) = 2 →
(1) + (-8) = 2 → 1 - 8 = 2 → -7 ≠ 2.
And (1, -2) → x + y = 3 → (1) + (-2) = 3 →
1 - 2 = 3 → -1 ≠ 3.
Lastly, Choice C is incorrect because
(1, -2) → 4x + y = 3 → 4(1) + (-2) = 3 →
4 + (-2) = 4 - 2 = 3 → 2 ≠ 3.
And (1, -2) → x - y = 2 → (1) - (-2) = 2 →
1 + 2 = 2 → 3 ≠ 2.
Therefore D is correct because it is the last answer remaining.
Also here is proof:
(1, -2) → 4x + y = 2 → 4(1) + (-2) = 2 →
4 + (-2) = 2 → 4 - 2 = 2 → 2 = 2
So one equation fits the coordinate, but this cannot yet be verified as the working system unless both equations fit the point.
So (1, -2) → x - y = 3 → (1) - (-2) = 3 →
1 + 2 = 3 → 3 = 3
Now we can say that this is the working system.
_____________________________
The next method involves strong observation of the graph to find both equations in slope-intercept form and then back into standard form to find a match of the choice answers as both systems are in standard form (Ax + By = C)
With the first line, it has a y-intercept of 2 because this is where it crosses the y-axis when x = 0. It also has a slope of -4 because it goes down 4 units every 1 unit to the right. This means that the first line has an equation of y = - 4x + 2.
Slope intercept form is the form y = mx + b where m is the slope( rise over run/change in y over change in x) , and b is the y-intercept (where x = 0).
The next line has a y-intercept of -3 because this is where it crosses the axis, and where x = 0. This also has a slope of 1 because it rises by 1 every run or goes up 1 unit every 1 unit to the right. therefore the second line has an equation of y = x - 3.
Related Questions
Given circle E with diameter CD and radius EA. AB is tangent to E at A. If AB=34 and EB=38, solve for EA. Round to the nearest tenth if necessary
Answers
The value of side EA is,
EA = 16.9
We have to given that;
Circle E with diameter CD and radius EA.
And, AB is tangent to E at A.
Here, AB = 34 and EB = 38
Hence, By using Pythagoras theorem we get;
AB² + AE² = EB²
34² + AE² = 38²
1156 + AE² = 1444
AE² = 1444 - 1156
AE² = 288
AE = √288
AE = 16.9
Thus, The value of side EA is,
EA = 16.9
Learn more about the circle visit:
https://brainly.com/question/24810873
#SPJ1

How do you do this question?
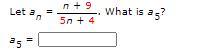
Answers
Answer:
14/29
Step-by-step explanation:
Simply substitute 5 for n.
a₅ = (5 + 9) / (5×5 + 4)
a₅ = 14 / 29
What is the scale factor between 4 cm and 10 cm?
B:10 cm
A:4 cm
Answers
Answer: B
Step-by-step explanation:
To find a scale factor between two similar figures, find two corresponding sides and write the ratio of the two sides. If you begin with the smaller figure, your scale factor will be less than one. If you begin with the larger figure, your scale factor will be greater than one. The ratio of any two corresponding lengths in two similar. geometric figures. Corresponding Angles: Angles in matching locations of two shapes
1 point
An arrow is launched upwards. The height of the arrow, in meters, after seconds can be modeled by the function h (t) = -2.1t2 +32t-0.03. After how many seconds will the arrow
first reach an altitude of 60 meters?
3.4 seconds
-8 seconds
2.2 seconds
13 seconds
Answers
The arrow first reach an altitude of 60 meters is 13 seconds.
A General Rule for Solving Equations
Simplify each side of the equation by removing parentheses and combining like terms.Use addition or subtraction to isolate the variable term on one side of the equation.Use multiplication or division to solve for the variable.Finding the value of the given equation's unknown variables is a step in the equation-solving process.The value of the variable satisfies the requirement that the two expressions are equal. When a linear equation has one variable, there is only one solution; when there are two variables, there are two solutions. A quadratic equation's solution yields two roots. To solve an equation, a variety of techniques and steps are used.h (t) = -2.1t² +32t-0.03 ---(i)
The arrow first reach an altitude of 60 meters:
h(t) = 60 -- (ii)
Equate the (i) and (ii)
60 = -2.1t² +32t-0.03
2.1t² - 32t + 0.03 + 60 = 0
2.1t² - 32t + 600.3 + = 0
t = -13, 13
Hence, The arrow first reach an altitude of 60 meters is 13 seconds.
To know more about equations check the below link:
https://brainly.com/question/22688504
#SPJ1
Given two parallel lines cut by a transversal,solve for x.

Answers
Answer:
x=3
Step-by-step explanation:
make it equal 0 since 2x^2=4x+30
0=2x^2+4x+30 then you factor out the 2
2(x^2+2x+15) then you factor and get
2(x+5)(x-3)
So x=-5 or x=3 and x cannot be negative
heyyy I need this done in 30 min please someone helppp

Answers
Answer:
1979
91%
Step-by-step explanation:
Given the relation :
P = (318t + 6792) / (1.19t + 107.36)
P = % of household with PC
t = years since 2000
1.) We need to find t, when P = 85%
P = 0.85
0.85 = (318t + 6792) / (1.19t + 107.36)
0.85(1.19t + 107.36) = (318t + 6792)
1.0115t + 91.256 = 318t + 6792
Collect like terms :
1.0115t - 318t = 6792 - 91.256
−316.9885t = 6700.744
t = 6700.744 / - 316.9885
t = - 21.138760
t = - 21 years
2000 - 21 years = 1979
Percentage who had computer in 2014
t = 2014 - 2000 = 14
P = (318(14) + 6792) / (1.19(14)+ 107.36)
P = (4452 + 6792) / (16.66 + 107.36)
P = 11244 / 124.02
P = 90.6627
P = approximately 91%
Answer of question 3 pls

Answers
The highest point for the quadratic function for the height of the object, h(t) = -16·t² + 224·t + 816, indicates that the interval over which the height of the object is increasing is; (-∞, 7]
What is the shape of the graph of a quadratic function?The shape of the graph of a quadratic function is a parabola.
The function for the height of the object in question 3 is; h(t) = -16·t² + 224·t + 816
Where;
t = The time in seconds
The height of the object is increasing in the interval to the left of the highest point, which can be found as follows;
The x-coordinate of the highest point of the quadratic function, f(x) = a·x² + b·x + c is; x = -b/(2·a)
Therefore, the x-coordinates of the highest point of the object is; -224/(2 × (-16)) = 7
Therefore, the height of the object is increasing in the interval; -∞ < t ≤ 7
Learn more on quadratic functions here: https://brainly.com/question/27920694
#SPJ1
What are the coordinates of the point on the directed line segment from ( − 7 , 9 ) (−7,9) to ( 3 , − 1 ) (3,−1) that partitions the segment into a ratio of 2 to 3?
Answers
The coordinates of the point on the directed line segment from (-7, 9) to (3, -1) that partitions the segment into a ratio of 2 to 3 are (-3, 5).
To find the coordinates of the point that divides the directed line segment from (-7, 9) to (3, -1) into a ratio of 2 to 3, we can use the section formula.
Let's label the coordinates of the desired point as (x, y). According to the section formula, the x-coordinate of the point is given by:
x = (2 * 3 + 3 * (-7)) / (2 + 3) = (6 - 21) / 5 = -15 / 5 = -3
Similarly, the y-coordinate of the point is given by:
y = (2 * (-1) + 3 * 9) / (2 + 3) = (-2 + 27) / 5 = 25 / 5 = 5
Therefore, the coordinates of the point that divides the line segment in a ratio of 2 to 3 are (-3, 5).
To understand this conceptually, consider the line segment as a distance from the starting point (-7, 9) to the ending point (3, -1). The ratio of 2 to 3 means that the desired point is two-thirds of the way from the starting point and one-third of the way from the ending point. By calculating the x and y coordinates using the section formula, we find that the desired point is located at (-3, 5).
For more such questions on segment
https://brainly.com/question/280216
#SPJ8
The circumference of a circle is 8π cm. What is the area, in square centimeters? Express your answer in terms of pi π.
Answers
The area of the circle with a circumference of 8π cm is: 16π cm².
What is the Area and Circumference of a Circle?Area = πr²Circumference = 2πrRadius of circle = rGiven:
Circumference = 8π cm
Find radius (r):
8π = 2πr
8π/2π = r
4 = r
r = 4 cm
Find area of circle:
Area = πr² = π(4)²
Area = 16π cm²
Learn more about area of circle on:
https://brainly.com/question/12269818
What is the volume of the rectangular box whose length is 5cm,width is 4 cm and height is 2 cm
Answers
Answer:
V = 40 cm3
Step-by-step explanation:
I found this answer by multiplying 5 x 4 x 2 to get the answer as 40.
5 x 4 = 20
20 x 2 = 40 cm3.
-SOPHIA
thank you for your help.

Answers
Answer:
q = -15
Step-by-step explanation:
5q = -75
Divide both sides by 5 : q = -15
100 Points! Algebra question, photo attached. Please show as much work as possible. Thank you!

Answers
A. The distributions of the periods is that using the five number summary is that
The 7th Period has higher minimum and lower maximumThe 3rd period is more spread (from the quartiles)The 7th Period has higher medianB. The box and whisker plot of the periods is attached
A. Comparing the distributions of the periodsFrom the question, we have the following parameters that can be used in our computation:
7th Period
66, 72, 77, 78, 78, 80, 82, 84, 84, 87, 88, 88, 89, 89, 90 92, 92, 93, 94, 94 96, 96
3rd Period
52, 60, 62, 64, 64, 65, 68, 71, 72, 74, 75, 76, 78, 79, 83, 84, 85, 88, 89, 93, 94, 97
The distributions of the periods will be compared using the five-number summaries
Using a graphing tool, the five-number summaries are:
7th Period
Minimum: 66Lower Quartile Q1: 79.5Median: 88Upper Quartile Q3: 92.25Maximum: 963rd Period
Minimum: 52Lower Quartile Q1: 64.75Median: 75.5Upper Quartile Q3: 85.75Maximum: 97B. Creating a box and whisker plot of the periodsThe box and whisker plot of the periods is added as an attachment
From the box and whisker plot attached, we can see the five-number summaries of the periods
Read more about box plot at
https://brainly.com/question/3473797
#SPJ1

Ellen wishes to mix candyworth a dollar and 45 cents per pound with candy worth $3.74 per pound to form 27 lb of a mixture worth $3.06 per pound how many pounds of the more expensive candy should she use
Answers
Ellen wishes to mix candy worth $1.45 per pound with candy worth $3.74 per pound to form 27 pounds of a mixture worth $3.06 per pound.
Let x be pounds of candy worth $1.45 per pound
Then we can set up the following equation
\(1.45x+3.74(27-x)=3.06\cdot27\)Where (27 - x) represents the pounds of candy worth $3.74 per pound
Let us solve this equation for x
\(\begin{gathered} 1.45x+3.74(27-x)=3.06\cdot27 \\ 1.45x+100.98-3.74x=82.62 \\ 1.45x-3.74x=82.62-100.98 \\ -2.29x=-18.36 \\ 2.29x=18.36 \\ x=\frac{18.36}{2.29} \\ x=8.02\: lb\: \end{gathered}\)So, 8.02 pounds of less candy is required.
Whereas the pounds of more expensive candy will be
\(27-x=27-8.02=18.98\: lb\)Therefore, 18.98 pounds of the more expensive candy should be used.
You draw a rectangle with vertices at (-3.5,3), (3.5,3), (3.5,-3), and (-3.5,-3).
What is the perimeter and area of the rectangle?
Answers
The perimeter and the area of the rectangle are 26 units and 42 square units, respectively.
What is a rectangle?A rectangle is a quadrilateral with all four interior angles 90°.
Given that, the vertices of the rectangle are (-3.5,3), (3.5,3), (3.5,-3), and (-3.5,-3).
The length of the rectangle is:
l = 3.5 - (-3.5)
l = 3.5 + 3.5
l = 7
The width of the rectangle is:
w = 3-(-3)
w = 3 + 3
w = 6
The perimeter of the rectangle is given by:
P = 2 (l +w)
P = 2(7 + 6)
P = 26
The area of the rectangle is:
A = l × w
A = 7 × 6
A = 42
Hence, the perimeter and the area of the rectangle are 26 units and 42 square units, respectively.
Learn more on rectangles here:
https://brainly.com/question/15019502
#SPJ1
Mrs. Jacobson asked her students to write a word problem that describes the graph below.
Which word problem accurately describes the graph?
Answers
Answer:
where's the graph? I can't see it
I need help with Kahn academy

Answers
Answer:
A
Step-by-step explanation:
So we have the two equations (in point-slope form):
\(y-3=2(x-3)\text{ and}\\y+5=2(x+1)\)
Now, note that the slope of the two equations are the same. The slope is 2.
Therefore, we can be certain that these are parallel lines since parallel lines have the same slope.
Therefore, they are also not intersecting lines.
Eliminate C and D.
Let's expand the equations:
\(y-3=2x-6\\y+5=2x+2\)
Add 3 to both sides for the first. Subtract 3 for the second:
\(y=2x-3\\y=2x-3\)
So, we can see that the two equations are exactly the same.
Therefore, these the same line.
Our answer is A.
And we're done!
HELP I WILL GIVE BRAINLIEST IF RIGHT

Answers
Answer:
a
Step-by-step explanation:
Answer:
a
Step-by-step explanation:
I might be wrong but i'm pretty sure it's right
46. The table shows the temperature (in degrees) for eight consecutive days as well as the
respective number of ice cream cones an ice cream shop sold on each of these days.
Temperature 68 77 83 85 89 94 96 99
Number of Cones 403 447 457 465 489 503 543 576
About how many ice cream cones would you expect the shop to sell if the temperature one day
is 106 degrees? Find a line of best fit for this data and use it to make your prediction.
0579 cones
0585 cones
O 602 cones
(617 cones
Answers
A line of best fit for this problem is y = 5.08x + 46.59. The number of ice cream cones that you would expect the shop to sell if the temperature one day is 106 degrees is; 585 cones
How to find the line of best fit?A graph of the scatter plot and line of best fit is as shown in the attached file.
The temperature in this problem is the independent variable, or x. This is due to the fact that we are assuming that the particular number of ice cream cones sold will depend on the temperature. Therefore, we can say that the number of ice cream cones will be the dependent variable, or y.
Therefore in our graphing calculator, we will enter temperature in the first list and then the number of cones in the second.
Sequel to drawing the scatter plot, we run the linear regression; we get the values for a and b in our equation, y = ax + b:
a = 5.08
b = 46.59
Therefore, the equation is;
y = 5.08x + 46.59.
Entering our temperature of 106 degrees, for x gives;
y = 5.08(106) + 46.59
= 585.07
≈ 585
Read more about Line of best fit at; https://brainly.com/question/1441182
#SPJ1

Triangles Q R S and X Y Z are shown. Angles Q S R and X Z Y are right angles. Angles Q R S and X Y Z are congruent. The length of Y Z is 9, the length of X Z is 12, and the length of hypotenuse X Y is 15.
Given △QRS ~ △XYZ, what is the value of tan(Q)?
Three-fifths
Three-fourths
Four-fifths
Answers
Answer:three-fourths
Step-by-step explanation:
because my dad said it was right
185 for 4 tickets whats the price per ticket
Answers
The cost of each ticket is $46.25.
1. A ball has a 9-inch radius. Leave answers Volume = Surface Area =
Answers
The ball in shape of sphere. So radius of sphere is r = 9 in.
The formula for the volume of sphere is,
\(V=\frac{4}{3}\pi(r)^3\)Substitute the value in the formula to obtain the volume of ball.
\(\begin{gathered} V=\frac{4}{3}\pi\cdot(9)^3 \\ =3053.628 \\ \approx3053.63 \end{gathered}\)The formula for the surface area of ball is,
\(S=4\pi\cdot(r)^2\)Substitute the value in the formula to obtain the surface area.
\(\begin{gathered} S=4\pi\cdot(9)^2 \\ =1017.876 \\ \approx1017.88 \end{gathered}\)So answer.
Volume = 3053.63 inch cube
Surface area = 1017.88 inch square.
Choose all that apply.

Answers
Answer:
Step-by-step explanation:
Answer (D)

ind the first quartile for this list of numbers
38 41
97 83
65 55
91 96
5 80
22 89
31 100
69
Quartile 1 =
Answers
answer: 39.5
Step-by-step explanation:
arrange numbers in ascending order....
5,22,31,38,41,55,75,69,80,83,89,91,96,97,100
then find median of the arranged list of numbers
which is 69
after that find the median between the arranged numbers starting from 5 to the median which we found as 69
which will be 38 and 41
So we add those two numbers together and then divide them by 2 .....which will give u 39.5
if instead the triangle on the left had the same area as the circle on the right
Answers
If the triangle on the left had the same area as the circle on the right, it would require more resources and potentially be more unstable than the current configuration.
If the triangle on the left had the same area as the circle on the right, it would mean that the triangle would have to be larger than its current size. This is because the area of a circle is determined by the formula A=πr^2, where r is the radius of the circle.
Therefore, if the area of the circle is equal to the area of the triangle, the radius of the circle would have to be equal to the height of the triangle, and the base of the triangle would need to be wider.
This would result in a larger triangle with a greater surface area than the current triangle. The larger triangle would also have a longer perimeter, which would make it more difficult to enclose and would require more material to construct.
Additionally, the larger triangle would have a higher center of gravity, which could make it more difficult to balance and more prone to tipping over.
Overall, if the triangle on the left had the same area as the circle on the right, it would require more resources and potentially be more unstable than the current configuration.
It is important to consider both the area and the shape of an object when determining its practicality and effectiveness in a given situation.
For more such questions on triangle
https://brainly.com/question/17335144
#SPJ8
Pemdas is something we use to make zero pairsTrue or False
Answers
Answer
True
step-by-step explanation:
Pemdas is an acronym in mathematics
P = parentheses
E = exponent
M =Multiplication
D = Division
A = Addition
S = Substraction
Pemdas only tell us the order of operation to be calculated first.
Hence, Pemdas can also be used to make zero pair
A vacant city lot is being turned into a neighborhood garden. The neighbors want to fence in a triangular section of the lot and plant flowers there. The longest side of the triangle section is 8 feet shorter than twice the shortest side. The third side is 2 feet longer than the shortest side. The perimeter is 58 feet. How long is each side?
Answers
Step-by-step explanation:
=>>. Hello mate. (◕ᴗ◕✿)
= Given :-
perimeter of traingle = 58 feet
let the third side be. "X" feet longest side = (2x - 8) feet shorter side = (x + 2) feetPerimeter of traingle = sum of all three sides
=> A/q. ,
( x ) + ( 2x - 8 ) + ( x + 2) = 58. ✓✓✓
x + 2x - 8 + x + 2 = 58
=>. 4x - 6 = 58
=> 4x = 58 + 6
=> 4x = 64
=>. x = 64/4
=|. x = 16 feet
length of third side = 16 feet length of shorter side = 18 feet length of longest side = 24 feet
Hope it helps you.......
I NEED HELP PLEASE, THANKS! :)

Answers
Answer:
θ = {0, π/2, π, 3π/2, 2π} . . . . choice B
Step-by-step explanation:
In this equation, r will be a maximum where cos(4θ) is a maximum. That is where ...
4θ = 2kπ . . . . for some integer k
Dividing by 4 gives ...
θ = k(π/2)
θ = {0, π/2, π, 3π/2, 2π} . . . . matches choice B
__
You will note that the graph also has extremes at odd multiples of π/4. These are the locations where cosine is a minimum and r is negative. It can be argued that r is not a maximum at those points.

Find the volume of the following solid. The solid in the first octant bounded by the coordinate planes and the surface zy
Answers
Answer:
The answer is "\(\frac{324}{5}\)"
Step-by-step explanation:
If the missing value is this \(z= 9-y-x^2\) then:
\(\bold{z =9-y-x^2} \\\\\to x\leq 0 \\\\\to y < 0\\\\let: \ z= 0\ then\\\\ \to 9-y-x^2=0\\\\\to y=9-x^2\\\\if\ y=0 \\\\\to 0=9-x^2\\\\\to x=3\\\\\text{Calculate the volume: }\\\)
\(\to \int \int z dz\ \ = \int \int_{R} (9-y-x^2) dz\\\\\)
\(=\int_0^{3} \ \int_0^{9-x^2} (9-y-x^2) dy \ dx\\\\=\int_0^{3} (9y- \frac{y^2}{2}-x^2 y)^{9-x^2} _{y=0}\ dx\\\\=\int_0^{3} (9-x^2)^2- \frac{(9-x^2)^2}{2}\ dx\\\\=\frac{1}{2} \int_0^{3} (9-x^2)^2\ dx\\\\=\frac{1}{2} \int_0^{3} 81+x^4-18x^2 \ dx\\\\=\frac{1}{2} (81x +\frac{x^5}{5}-6x^3)^3_0 \\\\= \frac{1}{2} (\frac{648}{5}) \\\\=\frac{324}{5}\)
Selling Price = $ 504 and Gain % = 12%
Answers
Answer:
Step-by-step explanation:
sp = 504
gain = 12%
in this case
sp =100%+12%=504
112%=504
1%=504/112 =4.5
100%=450
so cost =$450
Hope im correct, if i am im glad to be of service.
Solve the following equation
(1) 7x2 + 2x - 1 = 0
Answers
Answer:
-6.5
Step-by-step explanation: