At the school bookstore, Rylan bought two spiral notebooks and one folder and paid $6. 70. Olivia bought three spiral notebooks and five folders and paid $12. 85. Find the cost of each folder
Answers
To find the cost of each folder, we need to first set up a system of equations based on the given information. Let x be the cost of a spiral notebook and y be the cost of a folder. We can create the following equations:
1) 2x + y = $6.70 (Rylan's purchase)
2) 3x + 5y = $12.85 (Olivia's purchase)
First, we can solve equation 1 for y:
y = $6.70 - 2x
Next, substitute this expression for y into equation 2:
3x + 5($6.70 - 2x) = $12.85
Now, solve for x:
3x + $33.50 - 10x = $12.85
Combine like terms:
-7x = -$20.65
Now, divide by -7:
x = $2.95
Now that we know the cost of a spiral notebook, we can plug this value back into the expression we found for y:
y = $6.70 - 2($2.95)
y = $6.70 - $5.90
y = $0.80
So, the cost of each folder is $0.80.
To Know more about cost refer here
https://brainly.com/question/15135554#
#SPJ11
Related Questions
5. Prolific uses the bike in his trunk to find a nearby gas station with a mechanic to fix his rental
car. He rides 1.5 mi to the first gas station, where they say the next gas station may have a
mechanic. He then rides 1.6 mi to the next gas station, which also has no mechanic. The
following gas stations at 1.8 mi, 2.1 mi, and 2.5 mi away all have no mechanics available, but
confirm that there is a mechanic at the following gas station.
A. Assuming the rate remains constant, what equation will determine the distance of
the N gas station?
B.
If the pattern continues, how many miles will Prolific bike to get to the mechanic at
the 6th gas station?
Answers
Prolific will bike 2 miles to get to the mechanic at the 6th gas station if the pattern continues.
Assuming the rate remains constant, we can use the equation d = rt, where d is the distance, r is the rate, and t is the time. In this case, we want to find the equation to determine the distance of the Nth gas station.
Let's analyze the given information:
The first gas station is 1.5 miles away.
From the second gas station onwards, each gas station is located at a distance 0.1 miles greater than the previous one.
Based on this pattern, we can write the equation for the distance of the Nth gas station as follows:
d = 1.5 + 0.1(N - 1)
B. To find the distance Prolific will bike to get to the 6th gas station, we can substitute N = 6 into the equation from part A:
d = 1.5 + 0.1(6 - 1)
= 1.5 + 0.1(5)
= 1.5 + 0.5
= 2 miles
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
true or false: with a classic update using linear function approximation, we will always converge to some values, but they may not be optimal. why?
Answers
The statement is true. With a classic update using linear function approximation, we will always converge to some values, but they may not be optimal. This is because linear function approximation only allows for a limited representation of the value function, and the approximated function may not capture the true underlying structure of the problem.
Linear function approximation is commonly used in reinforcement learning to estimate the value function. The idea is to approximate the value function using a linear combination of features. During the learning process, the weights of the linear combination are updated using the classic update rule. While this approach is computationally efficient, it can result in suboptimal policies. The reason for this is that the approximated function may not be able to capture the complexity of the problem. This can lead to inaccuracies in the value function estimates, which in turn can result in suboptimal policies. To address this issue, more advanced function approximation methods, such as neural networks, can be used to approximate the value function. These methods can capture more complex relationships in the data and provide more accurate estimates of the value function.
To learn more about Linear function approximation : brainly.com/question/31584940
#SPJ11
a) estimate the area under the graph of f(x) = 5 cos(x) from x = 0 to x = /2 using four approximating rectangles and right endpoints. (round your answers to four decimal places.)
Answers
The estimated area under the graph of f(x) = 5 cos(x) from x = 0 to x = π/2 using four approximating rectangles and right endpoints is approximately 0.8916.
To estimate the area under the graph of f(x) = 5 cos(x) from x = 0 to x = π/2 using four approximating rectangles and right endpoints, we can use the right Riemann sum method.
The width of each rectangle, Δx, is given by the interval width divided by the number of rectangles.
In this case, Δx = (π/2 - 0)/4 = π/8.
To calculate the right endpoint values, we evaluate f(x) at the right endpoint of each rectangle.
For the first rectangle, the right endpoint is x = π/8.
For the second rectangle, the right endpoint is x = π/4.
For the third rectangle, the right endpoint is x = 3π/8.
And for the fourth rectangle, the right endpoint is x = π/2.
Now, let's calculate the area for each rectangle by multiplying the width (Δx) by the corresponding height (f(x)):
Rectangle 1: Area = f(π/8) * Δx = 5cos(π/8) * π/8
Rectangle 2: Area = f(π/4) * Δx = 5cos(π/4) * π/8
Rectangle 3: Area = f(3π/8) * Δx = 5cos(3π/8) * π/8
Rectangle 4: Area = f(π/2) * Δx = 5cos(π/2) * π/8
Now, let's calculate the values:
Rectangle 1: Area = 5cos(π/8) * π/8 ≈ 0.2887
Rectangle 2: Area = 5cos(π/4) * π/8 ≈ 0.3142
Rectangle 3: Area = 5cos(3π/8) * π/8 ≈ 0.2887
Rectangle 4: Area = 5cos(π/2) * π/8 ≈ 0
Finally, to estimate the total area, we sum up the areas of all four rectangles:
Total Area ≈ 0.2887 + 0.3142 + 0.2887 + 0 ≈ 0.8916
Therefore, the estimated area under the graph of f(x) = 5 cos(x) from x = 0 to x = π/2 using four approximating rectangles and right endpoints is approximately 0.8916.
To know more about endpoints refer here:
https://brainly.com/question/31398203#
#SPJ11
Consider the LP below. The BFS ("corners") are (0,0) (0,4) (1,4) (3,2) (3,0). The optimal solution is at x_{1} = 3 and x_{2} = 2
max z = 2x_{1} + x_{2}
s.t.
matrix x 1 +x 2 &<= 0 \\ x 1 &<=3\\ x 2 &<4 matrix
x_{1}, x_{2} >= 0
(a). What is the range of c_{1} the objective coefficient of x_{1} (currently 2) for which this BFS remains optimal:
(b). What is the range of b_{2} the right hand side of the second constraint (currently 3) for which this BFS remains optimal:
(c). What is the dual price of the second constraint?
Answers
(a) The range of c₁ (the objective coefficient of x₁) for which this BFS remains optimal is c₁ ≤ 2.
(b) The range of b₂ (the right-hand side of the second constraint) for which this BFS remains optimal is 3 ≤ b₂ < 4.
(c) The dual price of the second constraint is 0.
(a) The optimality condition for a linear programming problem requires that the objective coefficient of a non-basic variable (here, x₁) should not increase beyond the dual price of the corresponding constraint. In this case, the dual price of the second constraint is 0, indicating that increasing the coefficient of x₁ will not affect the optimality of the basic feasible solution. Therefore, the range of c₁ for which the BFS remains optimal is c₁ ≤ 2.
(b) The range of b₂ for which the BFS remains optimal is determined by the allowable range of the corresponding dual variable. In this case, the dual price of the second constraint is 0, implying that the dual variable associated with that constraint can vary within any range. As long as 3 ≤ b₂ < 4, the dual variable remains within its allowable range, and thus, the BFS remains optimal.
(c) The dual price of a constraint represents the rate of change in the objective function value per unit change in the right-hand side of the constraint, while keeping all other variables fixed. In this case, the dual price of the second constraint is 0, indicating that the objective function value does not change with variations in the right-hand side of that constraint.
Learn more about coefficient
brainly.com/question/1594145
#SPJ11
A house purchased 5 years ago for $100,000 was just sold for $135,000. Assuming exponential growth, approximate the annual growth rate, to the nearest percent.
Answers
The approximate annual growth rate of the house is 7.08% (to the nearest percent). This is determined using the formula for exponential growth, where the initial value of the house is $100,000 and the final value after 5 years is $135,000.
To determine the approximate annual growth rate of a house purchased for $100,000 and sold for $135,000 after 5 years, we can use the concept of exponential growth. Exponential growth refers to a continuous compounding process where the value of an investment increases over time based on a fixed growth rate.
Let's denote the initial value of the house as P₀ (P-subscript-0) and the final value as Pₙ (P-subscript-n). The growth rate can be represented by the formula:
Pₙ = P₀ × (1 + r)^n,
where r is the annual growth rate as a decimal and n is the number of years.
In this case, P₀ = $100,000, Pₙ = $135,000, and n = 5. We can plug these values into the equation and solve for r:
$135,000 = $100,000 × (1 + r)^5.
To isolate (1 + r)^5, we divide both sides of the equation by $100,000:
(1 + r)^5 = $135,000 / $100,000.
(1 + r)^5 ≈ 1.35.
To find the annual growth rate, we take the fifth root of both sides:
1 + r ≈ (1.35)^(1/5).
1 + r ≈ 1.0708.
Subtracting 1 from both sides, we get:
r ≈ 0.0708.
The approximate annual growth rate is 0.0708, or 7.08% to the nearest percent.
To know more about exponential growth, refer here:
https://brainly.com/question/1596693#
#SPJ11
how to find the square root of 1225
Answers
Hope i helped
Answer:
35
Step-by-step explanation:
The square root is 35 because if you multiply 35 times 35 (\(35^{2}\)), it would equal 1225.
Hope this helps and pls do mark me brainliest if you can:)
I need help immediately :(((

Answers
Answer: $118.00
Step-by-step explanation:
Answer:
18.8 I'm not sure though
what is negative 7/4 as a decimal
Answers
Answer:
-1.75
Step-by-step explanation:
1.75 is a decimal and 175/100 or 175% is the percentage for 7/4.
A distribution of probabilities for random outcomes of a bivariate or dichotomous random variable is called a Group of answer choices binomial probability distribution distribution of expected values random variable distribution mathematical expectation
Answers
A distribution of probabilities for random outcomes of bivariate or dichotomous random variables is called (A) binomial probability distribution.
What is a binomial probability distribution?The binomial distribution with parameters n and p in probability theory and statistics is the discrete probability distribution of the number of successes in a succession of n separate experiments, each asking a yes-no question and each with its own Boolean-valued outcome: success or failure.The binomial distribution is widely used to describe the number of successes in a sample of size n selected from a population of size N with replacement. If the sampling is done without replacement, the draws are not independent, and the resulting distribution is hypergeometric rather than binomial. Binomial probability distribution refers to a distribution of probabilities for random outcomes of bivariate or dichotomous random variables.As the description itself says, binomial probability distribution refers to a distribution of probabilities for random outcomes of bivariate or dichotomous random variables.
Therefore, a distribution of probabilities for random outcomes of bivariate or dichotomous random variables is called (A) binomial probability distribution.
Know more about binomial probability distribution here:
https://brainly.com/question/9325204
#SPJ4
Complete question:
A distribution of probabilities for random outcomes of bivariate or dichotomous random variables is called a ______.
Group of answer choices
(A) binomial probability distribution
(B) distribution of expected values
(C) random variable distribution
(D) mathematical expectation
Teah was selling candy bars for a fundraiser. She spent $25 on a box of candy bars and sold each candy bar for $2.50. Her profit was $75. Teah wrote the equation 2.5c−25=75 for this situation, and she found c=40. Which statement is true about the solution c=40?
Answers
Answer:
The equation is not true. It is actually c=30
Step-by-step explanation:
First you have to divide amount of money she's selling the candy bars for which is $2.50.
If her profit was $75, you want to know how much bars she sold, you will have to divide the amount of money she's selling the candy bars for and the amount she's earning which is $75 divided by $2.50 which is 30.
So c= 30
Planes A and B intersect in line s. If point Vis a point on line s, then it lies on:
O plane A only
plane B only
both plane A and B
neither plane A or B
Answers
Answer:
Option C.
Step-by-step explanation:
It is given that planes A and B intersect in line s.
It means, all points lie on the line s must be lie on both plane A and B because s is the line of intersection of both plane A and B.
It is given that V is a point on line s.
Since, the point V lies on line s, therefore it is also lies on both plane A and B.
Hence, the correct option is C.
which function k(x) shows the graph of h(x)=-2^x+3 shifted left 7 units and down 5 units?
Answers
To shift the graph of h(x) = -2^x+3 left 7 units and down 5 units, we need to modify the equation as follows:
k(x) = -2^(x+7) - 5
Here's how we arrived at this equation:
To shift the graph left 7 units, we need to subtract 7 from x, so we have:
h(x+7) = -2^x+3
To shift the graph down 5 units, we need to subtract 5 from the entire function, so we have:
h(x+7) - 5 = -2^x+3 - 5
Simplifying the right-hand side of the equation, we get:
h(x+7) - 5 = -2^x-2
Finally, substituting h(x+7) with its original expression, we get:
k(x) = -2^(x+7) - 5
Therefore, the function k(x) that shows the graph of h(x)=-2^x+3 shifted left 7 units and down 5 units is k(x) = -2^(x+7) - 5.
Solve for X. Plz help me

Answers
Answer:
x = 20
Step-by-step explanation:
\((2x) \degree + x \degree+ 60 \degree + (360 - 120) \degree = 360 \degree \\ \\ (3x) \degree+ 60 \degree + 240 \degree = 360 \degree \\ \\ (3x) \degree+ 300 \degree = 360 \degree \\ \\ 3x = 360 \degree - 300 \degree\\ \\ (3x ) \degree= 60 \degree \\ \\ 3x = 60 \\ \\ x = \frac{60}{3} \\ \\ x = 20 \)
What is the greatest decimal place value?
Answers
Answer:
Millionths
Step-by-step explanation:
It is the fartherst decimal place that thier is.
Select the correct answer from each drop-down menu.
• Drop down box 1
Division property of equality
Multiplication property of equality
Substitution property of equality
• Drop down box 2
csin(A) = bsin(C)
ccos(B) =bcos(C)
csin(B) =bsin(C)
• Drop down box 3
Division property of equality
Multiplication property of equality
Substitution property of equality
Really need this answer please

Answers
We can see here that in selecting the correct answer, we have:
Drop down box 1: Multiplication property of equality.
Drop down box 2: csin(B) =bsin(C)
Drop down box 3: Division property of equality.
What is Multiplication property of equality?A key idea in algebra is the multiplication property of equality, which asserts that if we multiply both sides of an equation by the same non-zero number, the equality is still maintained.
In other words, if a = b, then for any non-zero number c, we have:
a × c = b × c
Algebraic equations and expressions are frequently solved using the multiplication property of equality, a potent tool.
Learn more about multiplication property of equality on https://brainly.com/question/29705007
#SPJ1
What is the smallest positive integer that is both a multiple of $7$ and a multiple of $4$?
Answers
The smallest positive integer that is both multiple of 4 and 7 is 2
What are multiples?In mathematics, multiples are the results of multiplying an integer by a given number.
The given numbers for this problem are 4 and 7. The positive multiples of 4 and 7 will be listed and the first number that appeared in the both multiples s the smallest positive integer that is both a multiple of 7 and a multiple of 4.
The multiples of 4
4 8 12 16 20 24 28 32 36 .......
The multiples of 7:
7 14 21 28 35 42 49 56 63 70 77 84 91 98 .....
The smallest common multiple is 28
Learn more about multiples at:
brainly.com/question/28923509
#SPJ1
Suppose the supply and demand equations for a product are given by: p²+4q = 253 183 p² + 6q0 - Find the equilibrium point, and enter it as a point. Equilibrium Quantity: q = Equilibrium Price: p =
Answers
The equilibrium point for the supply and demand equations p² + 4q = 253 and 183p² + 6q = 0 is (q, p) = (3, 10).
To find the equilibrium point, we need to solve the system of equations formed by the supply and demand equations. By substituting the value of q = 3 into the first equation, we get p² + 4(3) = 253, which simplifies to p² + 12 = 253.
Solving this equation gives us p = 10. Substituting the values of q = 3 and p = 10 into the second equation, we get 183(10)² + 6(3) = 0, which simplifies to 18300 + 18 = 0.
Since this equation holds true, we have found the equilibrium point to be (q, p) = (3, 10), where the equilibrium quantity is q = 3 and the equilibrium price is p = 10.
Learn more about Equation click here :brainly.com/question/13763238
#SPJ11
which name gives the most information about the shape below
Rhombus
Trapezoid
quadrilateral
Parallelogram
Answers
HELP ASAP!!!!
Enter the correct answer in the box.
The function f(x) = 2^x - 1 is transformed to function g through a horizontal shift of 7 units left. What is the equation of function g?
Replace the values of hand kin the equation.
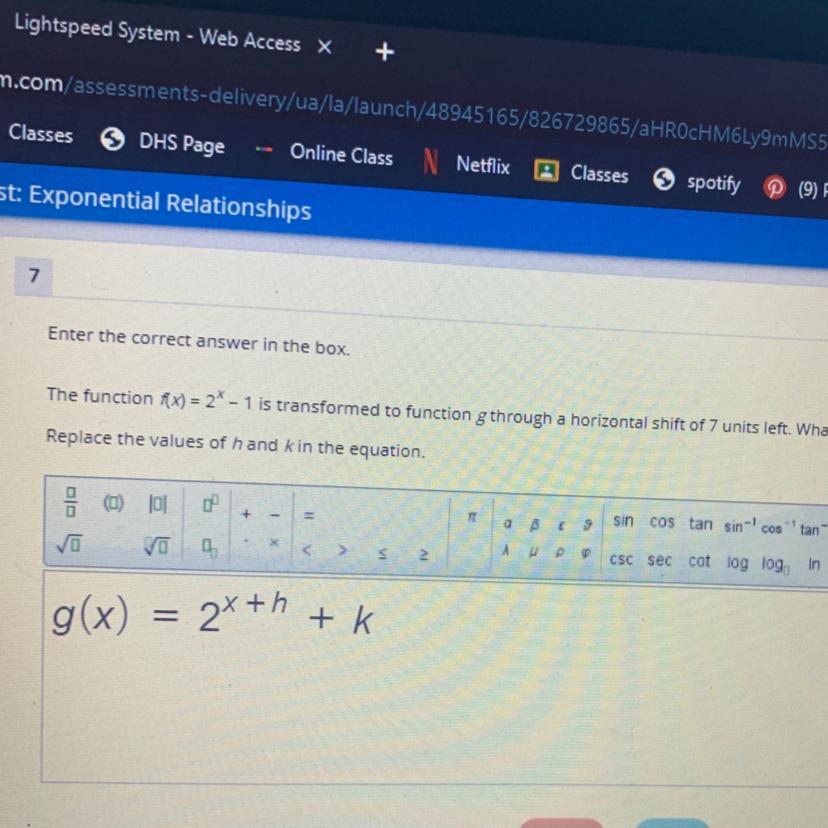
Answers
Answer:
h = 7, k = -1
Step-by-step explanation:
g(x) = f(x + 7)
g(x) = 2(x + 7) - 1
g(x) = 2(x + h) + k
h = 7, k = -1
Answer:
h=7 and k=-1
Step-by-step explanation:
Remember that the values of h and k represent horizontal and vertical shifts respectively. Therefore, because the transformation is a horizontal shift of 7 units to the left, then h=7 and k=-1.
Review the graph to observe the transformation

Which equation does the graph below represent
1) y = 2x
2) y = 1/2x
3) y = 1/2+x
4) y = 2+x

Answers
Answer:
y=1/2+x
1Beacuxse the negative is the postivw
It takes 4.5 hours for a ship traveling downriver to get from port A to port B. The return journey takes 6.3 hours. The river flows at 40 meters per minute. What is the distance between the two ports
Answers
The speed of the river is ...
.. (40 m/min)*(60 min/h)*((1 km)/(1000 m)) = 2.4 km/h
Here, we have,
speed = distance/time
Let d represent the distance between the ports. Let s represent the speed of the ship.
Downstream, we have
.. s +2.4 = d/4.5
.. s = d/4.5 -2.4
Upstream, we have
.. s -2.4 = d/6/3
.. s = d/6.3 +2.4
Now, we have the speed of the ship represented two ways. We assume the speed of the ship doesn't vary. so these are equal.
.. (d/6.3) +2.4 = (d/4.5) -2.4
.. 4.8 = d(1/4.5 -1/6.3) = d(4/63) . . . . . rearrange and simplify
.. 75.6 = d . . . . . . . . . . . . . . . . . . . . . . .multiply by 63/4
The distance between the two ports is 75.6 km.
To learn more on Distance click:
brainly.com/question/15172156
#SPJ12
expand the expression below to find the values of capatilised pronumerals
PLS HELP :))

Answers
»(4x - 2y)(3x + 5y)
»4x(3x + 5y) + (-2y)(3x + 5y)
»12x² + 15xy - 6xy - 10y²
»12x² + 9xy - 10y²
so, ABC is :
A = 12✅B = 9✅C = -10✅Whats the product 0.4(-1.08)
Answers
3480 divided by 29 what is the answer that its asked
Answers
Answer:
120
Step-by-step explanation:
To be honest I just looked it up.
Identify the area of the figure rounded to the nearest tenth

Answers
Answer:
118.7 inches squared.
Step-by-step explanation:
What is the area?The area is the total space taken up by a flat (2-D) surface or shape. The area is always measured in square units.
What is diameter?Diameter is the length across the entire circle, the line splitting the circle into two identical semicircles.
The expression for solving the area of a circle is A = π × \(r^{2}\).
To solve for the semicircle above, we can divide the diameter into 2 to get the radius.
12 ÷ 2 = 6So, the radius of the upper semicircle is 6 inches.
If the radius of a circle is 6 inches, then you can substitute r for 6 into the formula.
A = π × \(6^{2}\)This simplifies to A = 36π. If a semicircle if half the size of a normal circle, then it will be A = 18π, because 36 ÷ 2 = 18.
To solve for the lower semicircle, we can do the same this as we did above.
A = π × \(r^{2}\)But wait, we don't know the radius or diameter!
No worries! To solve for the diameter of the circle, we can take the line that is parallel to the semicircle (the one that has a length of 12in) and subtract 6 from it. We subtract 6 from it because the semicircle takes up the remaining length of the line, not including the 6in.
To solve for the lower semicircle, we can divide the diameter by 2 to get the radius.
6 ÷ 2 = 3So, the radius of the circle is 3.
Now we can insert 3 into the expression.
A = π × \(3^{2}\)This simplifies to A = 9π. If a semicircle if half the size of a normal circle, then it will be A = 4.5π because like above, 9 ÷ 2 = 4.5.
Adding the two semicircles together:
18π + 4.5π = 22.5π22.5 × π ≈ 70.6858So, the area of both semicircles is approximately 70.6858 square inches.
To solve for the area of a rectangle we use the expression:
A = length × widthInserting the dimensions of the rectangle:
8 × 6 = 48So, the area of the rectangle is 48 square inches.
Adding the two areas together:
70.6858 + 48 = 118.6858 ≈ 118.7Therefore, the area of the entire figure, rounded to the nearest tenth is \(118.7\) \(in^{2}\).
burgers cost $2.50 each and fries cost $1.30 each. if wendy spent $24.10 on 13 fries and burgers, how many of each did she buy?
Answers
If Wendy spent $24.10 on 13 fries and burgers, then she bought 6 burgers and 7 orders of fries.
Let x be the number of burgers Wendy bought and y be the number of fries she bought.
We know that burgers cost $2.50 each and fries cost $1.30 each.
So the total cost of x burgers and y fries is:
2.5x + 1.3y
We also know that Wendy spent $24.10 on 13 burgers and fries, so:
2.5x + 1.3y = 24.10
Finally, we know that Wendy bought a total of 13 burgers and fries:
x + y = 13
Now we have two equations with two variables, which we can solve using substitution or elimination.
Let's use substitution:
x = 13 - y
Substitute this into the first equation:
2.5(13 - y) + 1.3y = 24.10
Simplify and solve for y:
32.5 - 2.5y + 1.3y = 24.10
-1.2y = -8.4
y = 7
So Wendy bought 7 orders of fries.
Substitute y = 7 into x + y = 13 to find x:
x + 7 = 13
x = 6
So Wendy bought 6 burgers and 7 orders of fries.
Learn more about the subtraction visit:
https://brainly.com/question/17301989
#SPJ1
What is 200 increased by 50%?
.$50 decreased by 20% is how much?
.What amount increased by 130% is $49.39?
.What amount decreased by 20% is $480?
.$1,180 decreased by what percent equals $400?
.650 kg is what percent less than 1,700 kg ?
Answers
The answers are 1) 300, 2) 40, 3) 37.99, 4) 600, 5) 400 and 6) 1700.
To calculate these percentages, let's go through each question step by step:
1) What is 200 increased by 50%?
To find the increase, you can multiply 200 by 50% (or 0.5) and add it to 200:
200 + (200 × 0.5) = 200 + 100 = 300
So, 200 increased by 50% is 300.
2) $50 decreased by 20% is how much?
To find the decrease, you can multiply $50 by 20% (or 0.2) and subtract it from $50:
50 - (50 × 0.2) = 50 - 10 = $40
So, $50 decreased by 20% is $40.
3) What amount increased by 130% is $49.39?
To find the original amount, you need to divide $49.39 by 130% (or 1.3):
$49.39 / 1.3 = $37.99 (rounded to two decimal places)
So, an amount increased by 130% to reach $49.39 is approximately $37.99.
4) What amount decreased by 20% is $480?
To find the original amount, you need to divide $480 by 80% (or 0.8):
$480 / 0.8 = $600
So, an amount decreased by 20% to reach $480 is $600.
5) $1,180 decreased by what percent equals $400?
To find the percentage decrease, you can subtract $400 from $1,180 and divide the result by the original amount ($1,180).
Then multiply by 100 to get the percentage:
(($1,180 - $400) / $1,180) × 100 = (780 / 1180) × 100 = 0.661 × 100 ≈ 66.1%
So, $1,180 decreased by approximately 66.1% equals $400.
6) 650 kg is what percent less than 1,700 kg?
To find the percentage difference, you can subtract 650 kg from 1,700 kg, divide the result by the original amount (1,700 kg), and multiply by 100 to get the percentage:
((1,700 kg - 650 kg) / 1,700 kg) × 100 = (1,050 kg / 1,700 kg) × 100 ≈ 61.76%
So, 650 kg is approximately 61.76% less than 1,700 kg.
Learn more about percentages click;
https://brainly.com/question/32197511
#SPJ1
Bad gums may mean a bad heart. Researchers discovered that 77% of people who have suffered a heart attack had periodontal disease, an inflammation of the gums. Only 30% of healthy people have this disease. Suppose that in a certain community heart attacks are quite rare, occurring with only 14% probability. If someone has periodontal disease, what is the probability that he or she will have a heart attack?
Answers
The probability that a person with periodontal disease will have a heart attack is 45.9%.
To find the probability, we need to use Bayes' theorem, which relates the probability of having a heart attack given that the person has periodontal disease (P(A|B)) to the probability of having periodontal disease given that the person had a heart attack (P(B|A)), the probability of having a heart attack (P(A)), and the probability of having periodontal disease (P(B)):
P(A|B) = P(B|A) * P(A) / P(B)
Using the given information, we have:
P(B|A) = 0.77 (77% of heart attack patients have periodontal disease)
P(A) = 0.14 (14% probability of heart attack)
P(B) = 0.3 (30% of healthy people have periodontal disease)
Plugging these values into the formula, we get:
P(A|B) = 0.77 * 0.14 / 0.3 = 0.459 or 45.9%
Therefore, if someone has periodontal disease, the probability that they will have a heart attack is 45.9%.
You can learn more about probability at
https://brainly.com/question/25839839
#SPJ11
Learning Task 3. Encircle
notebook.
Rational Algebraic
Expression. Do this in your
1
1. 6x-1
2
2, x2 + x - 3
3.
x2 - 4
- 2
*
5.
1 름
3x
B. Simplify the following rational algebraic expression.
4m2
abc
x +1
1. 2m
2. bc
3. x2-4x-5
Answers
Algebraic expressions are expressions that use literals (i.e alphabets) to represent its variables.
The rational expressions are: \(\frac{2}{3x}\) and \(\frac{x^2 - 4}{x - 2}\).The simplified expressions are: \(2m\), \(a\) and \(\frac 1{x - 5}\)(a) Encircle Rational Algebraic Expressions
A rational algebraic expression is a ratio of two polynomials.
So, the rational expressions are:
\(\frac{2}{3x}\) and \(\frac{x^2 - 4}{x - 2}\) because the numerator and the denominator are polynomials
However,
\(6x - 1\), \(x^2 + x - 3\) and \(\frac{1}{x^{-5}}\) are not rational
(b) Simplify
\(\frac{4m^2}{2m}\)
Expand the numerator
\(\frac{4m^2}{2m} = \frac{2m \times 2m}{2m}\)
Cancel out 2m
\(\frac{4m^2}{2m} = 2m\)
\(\frac{abc}{bc}\)
Expand the numerator
\(\frac{abc}{bc} = \frac{a \times bc}{bc}\)
Cancel out bc
\(\frac{abc}{bc} = a\)
\(\frac{x + 1}{x^2 - 4x - 5}\)
Expand the denominator
\(\frac{x + 1}{x^2 - 4x - 5} = \frac{x + 1}{x^2 - 5x + x - 5}\)
Factorize
\(\frac{x + 1}{x^2 - 4x - 5} = \frac{x + 1}{x(x - 5) + 1(x - 5)}\)
Factor out x - 5
\(\frac{x + 1}{x^2 - 4x - 5} = \frac{x + 1}{(x + 1)(x - 5)}\)
Cancel out the common factor
\(\frac{x + 1}{x^2 - 4x - 5} = \frac{1}{x - 5}\)
Read more about algebraic expressions at:
https://brainly.com/question/11227332
Write the equation of the line fully simplified slope-intercept form

Answers
Cause slope is -4/1
Y-intercept is -6
Answer:
y=-3x+6
Step-by-step explanation:
that might not be fully simplified, but that should be the equation