Between which two integers does 7/3 lie Answer A 4 and 5 Answer B 1 and 2 Answer C 2 and 3 Answer D 3 and 4

Hey there,

We have,

f(x) = x² + 11x + 30g(x) = x + 6

Now,

(f.g)(x) = f(g(x))

Substituting...

g(x) = x + 6f(g(x)) = f(x + 6)

Now,

f(x + 6)= (x + 6)² + 11(x + 6) + 30= x² + 12x + 36 + 11x + 66 + 30= x² + 23x + 132

So,The value is x² + 23x + 132

Answer:

21x^2 + 7x

Step-by-step explanation:

The formula for the area of a rectangle is L x W. The length in this case is 3x+1 and the width is x. Multiply those together and you get 3x^2 + x.

The formula for the area of a triangle is 1/2BH. When you plug in the numbers, the area of the triangle is 24x^2 + 6x.

Now, you want to subtract the area of the triangle from the area of the rectangle. When you do this, you get your answer: 21x^2 + 7x.

The number of ways to arrange n men and n women in a row such that the men and women alternate is 2(n!)^2. This can be solved by the concept of Permutation and combination.

To see why, consider that there are n! ways to arrange the n men and n! ways to arrange the n women. Once the gender of the person in the first position is determined, the gender of the person in the second position is also determined. Therefore, there are only 2 possibilities for the first two positions. Similarly, once the genders of the first two positions are determined, the genders of the next two positions are also determined, resulting in only 2 possibilities for the next two positions. This pattern continues until all n men and n women have been placed in the row.

Therefore, the total number of ways to arrange the group is 2(n!)^2.

To learn more about Permutation and combination here:

brainly.com/question/13387529#

#SPJ11

Answer:

the answer I got is ×=7/15

so the answer is D

Answer:

D. None of The Above

Step-by-step explanation:

Answer:

it is a rational number

Step-by-step explanation:

hope dis helps ;D

Answer:

irrational

Step-by-step explanation:

A rational number is one that can be written as the ratio of two integers. For example 3=3/1, −17, and 2/3 are rational numbers.So in that case 2/3 is irrational.

the expression that is a factor of the fourth term in the expansion of (x^4 + y^7)^z is C) x^3.The fourth term in the expansion of the expression (x^4 + y^7)^z can be found using the binomial theorem:

T4 = (z choose 3) * (x^4)^(z-3) * (y^7)^3

where "z choose 3" is the binomial coefficient that represents the number of ways to choose 3 items from z items.

Simplifying this expression, we get:

T4 = (z choose 3) * x^(4z-12) * y^21

To determine which expression is a factor of T4, we need to find the common factors of x^(4z-12) and y^21 that are also factors of the other given expressions.

Option A, x^2, is not a factor of T4 because x^(4z-12) does not necessarily contain x^2 as a factor.

Option B, y^7, is not a factor of T4 because y^21 does not necessarily contain y^7 as a factor.

Option C, x^3, is a factor of T4 because x^(4z-12) contains x^3 as a factor.

Option D, y^3, is not a factor of T4 because y^21 does not necessarily contain y^3 as a factor.

Therefore, the expression that is a factor of the fourth term in the expansion of (x^4 + y^7)^z is C) x^3.

To  learn  more about expression click here:brainly.com/question/14083225

#SPJ11

3 x 3 is the prime factorization of 9.

What is a Prime factor?

A natural number other than 1 in which the only factors are 1 and on its own is referred to as having a prime factor.

In fact, the first five prime numbers are 2, 3, 5, 7, 11, and so forth.

How is the prime factor determined?

To use the division method to determine a number's prime factors, follow the following steps:

Step 1 : Divide the specified integer by the smallest prime number as the

Step 2 : Divide the quotient yet again by the smallest prime number in

Step 3: Keep on in the same fashion until the quotient reaches 1.

Step 4: Multiply all the prime factors at the conclusion.

The average of the nine elements is what?

Average is the result of dividing the total by a certain number.

To know more about Prime Factor visit :

https://brainly.com/question/29775157

#SPJ4

Answer:

68

Step-by-step explanation:

Measure of arc = Measure of corresponding central angle

Thus, if the measure of an arc = 68, then the measure of its central angle also = 68

Answer:D

Step-by-step explanation: Nolan did nothing wrong

The correct statement is option (c)   No. The set of given vectors spans a plane in R⁴ Any of the three vectors can be written as a linear combination of the other two.

In this case, we are given three vectors {v₁, v₂, v₃} and asked whether they span the space R⁴, which is the space of all four-dimensional vectors. To answer this question, we can write these vectors as the columns of a matrix A, which looks like:

A = [v₁ v₂ v₃]

One way to check whether this is true is to row-reduce the matrix A to its row-echelon form. If every row of the row-echelon form has a pivot position, then the columns of A span R⁴. If not, then they do not span R⁴.

So, let's do that. When we row-reduce A, we get:

[ 1 0 -1 ]

[ 0 1 1 ]

[ 0 0 0 ]

[ 0 0 0]

As you can see, there is no pivot position in the fourth row of the row-echelon form. In other words, v3 can be written as a linear combination of v₁ and v₂. This means that the set {v₁, v₂, v₃} does not span all of R⁴, but only a plane in R⁴.

Therefore, the correct answer is C. The set of given vectors spans a plane in R⁴, and any of the three vectors can be written as a linear combination of the other two.

To know more about vector here.

https://brainly.com/question/29740341

#SPJ4

Answer: Range = 22 IQR = 13

Step-by-step explanation:

To find the range of a data set, subtract the largest value of the data set from the smallest value. 45 is the largest value and 23 is the smallest, and 45-23 is 22, so the range is 22. To find the IQR, you must subtract the upper quartile and the lower quartile. We can find this after finding the mean by re-arranging all the values in order from lowest to greatest, and finding the middle value. Once we do so, we get 33.5. Then, we find the median of all the numbers below and after the median to get the lower and upper quartiles. Then, we subtract them to get the IQR 13.

Answer:

Yes, this is an arithmetic sequence.

The difference is -3, so a(n+1) = a(n) - 3

The 21st term is -53, calculated as follows:

a(21) = 7 + (21 - 1)(-3) = -53

The next three terms are -5, -8, and -11.

There are certainly hidden variables, which is the most likely explanation for this correlation. (C) States with large populations, for instance, will also have a larger percentage of infant death and high school dropouts.

When the values of one variable tend to rise as the values of the other rise, two variables are said to be positively correlated.

When the values of one variable tend to fall as the values of the other rise, two variables are said to be negatively correlated.

A favorable connection occurs when the graph's line is advancing, as in Problem 1.

In this illustration, we make the assumption that the number of years of schooling and the expected pay are positively correlated.

So, in the given situation the most likely explanation for this correlation is that there are likely lurking variables.

For instance, states with big populations will also have a higher proportion of neonatal mortality as well as high school dropouts.

Therefore, there are certainly hidden variables, which is the most likely explanation for this correlation. (C) States with large populations, for instance, will also have a larger percentage of infant death and high school dropouts.

Know more about the positive associations here:

https://brainly.com/question/1641078

#SPJ1

Complete question:

According to the 1990 census, those states with an above average number X of people who fail to complete high school tend to have an above average number Y of infant deaths. In other words, there is a positive association between X and Y. The most plausible explanation for this association is

a. X causes Y. Thus, programs to keep teens in school will help reduce the number of infant deaths.

b. Y causes X. Thus, programs that reduce infant deaths will ultimately reduce the number of high school dropouts.

c. lurking variables are probably present. For example, states with large populations will have both a larger number of people who fail to complete high school and a larger number of infant deaths.

d. the association between X and Y is purely coincidental. It is implausible to believe the observed association could be anything other than accidental.

The equation of the parabola in vertex form is

P is -\(\frac{1}{2}\)

(0,-\(\frac{1}{2}\))

y=\(\frac{-1}{2}\)\(x^{2}\) -\(\frac{1}{2}\)

A parabola is an approximately U-shaped, mirror-symmetrical plane curve in mathematics. It corresponds to a variety of seemingly unrelated mathematical descriptions, all of which may be shown to define the same curves.

One definition of a parabola includes a line and some extent  (the focus) (the directrix). The directrix isn't the main focus. The locus of points therein plane that is equally spaced apart from the directrix and the focus is known as the parabola. A right circular conical surface and a plane parallel to a different plane that is tangential to the conical surface intersect to form a parabola, which is additionally known as a conic section.

To  learn more about parabola  from the given link:

brainly.com/question/21685473

#SPJ9

Answer

he would have gotten a marry Christmas

Step-by-step explanation:

also hope you have a good day

The conditional probability of passing the second test, given that the student passed the first test, is approximately 0.857 or 85.7%.

The random variable X represents the outcome of the first test, where it takes on a value of 1 if the student passes and 0 if the student fails.

Similarly, the random variable Y represents the outcome of the second test, taking on a value of 1 if the student passes and 0 if the student fails. Given that the joint probability of passing both tests is 0.6, we can interpret this as the probability of X=1 and Y=1.

The marginal probability of failing the first test is 0.3, which can be represented as P(X=0). To find the conditional probability of passing the second test, given that the student passed the first test, we use the formula \(P(Y=1 | X=1) = P(X=1 and Y=1) / P(X=1).\)

Since we know that \(P(X=1 and Y=1) = 0.6, and P(X=1) = 1 - P(X=0) = 1 - 0.3 = 0.7\), we can substitute these values into the formula:
\(P(Y=1 | X=1) = 0.6 / 0.7\)

To know more about probability visit:

https://brainly.com/question/31828911

#SPJ11

The conditional probability of passing the second test, given that the student passed the first test, is approximately 0.8571 or 85.71%.

The conditional probability of passing the second test, given that the student passed the first test, can be calculated using the formula for conditional probability:

P(Y=1 | X=1) = P(X=1 and Y=1) / P(X=1)

We are given that the joint probability of passing both tests is 0.6, which means P(X=1 and Y=1) = 0.6.

To find P(X=1), we need to use the marginal probability of failing the first test, which is given as 0.3. Since the marginal probability of passing the first test is the complement of failing the first test (i.e., 1 - 0.3 = 0.7), we can say P(X=1) = 0.7.

Now we can substitute these values into the conditional probability formula:

P(Y=1 | X=1) = 0.6 / 0.7

Simplifying this expression, we have:

P(Y=1 | X=1) = 0.8571

Learn more about conditional probability:

https://brainly.com/question/30760899

#SPJ11

The correct option is Option 1 - 3520.

A farmer owns 3520 acres in which three full sections, four half-sections, and two quarter-sections are there.

Three of a farmer's sections were full. Let's say a full section is 640, which is

=3 x 640,

= 1,920.

He had four half portions as well. Divide 640 by two to get 320 (640/2), which is

= 4 X 320

= 1,280.

He had three quarter portions as well. Divide 640 by 4 to create a quarter piece (640/4 = 160)

= 2 X 160

= 320.

Now we have to add all these,

Three full sections       = 1920

Four half-sections        = 1280

Two quarter-sections  = 320

= 1,920 + 1,280 + 320

= 3,520.

Therefore the acres a farmer had is 3520.

For such more question on sections:

brainly.com/question/17297694

#SPJ4

The following question may be like this:

A farmer owns three full sections, four half-sections, and two quarter-sections. How many acres is this?

Answer:

41%

Step-by-step explanation:

12/29 8th graders spend more than 1 hour so the answer is 41%

Answer:

41%

Step-by-step explanation:

Number of 8th graders who spend more than an hour a day on social media/total eighth graders = 12/29 = 41%

There are 2571861957619336464277760000000 possible 6-word sentences that can be made using each of the 26 letters in the alphabet exactly once.

There are a couple of steps we need to take in order to find the number of 6-word sentences that can be made using each of the 26 letters in the alphabet exactly once.

Step 1: Find the number of full permutations of the 26 letters. This is given by 26! (26 factorial), which is equal to 403291461126605635584000000.

Step 2: Separate the full permutation into words by inserting spaces. Since we want to create 6-word sentences, we need to insert 5 spaces into the full permutation. There are 25 possible positions for the first space, 24 for the second, 23 for the third, 22 for the fourth, and 21 for the fifth. So the number of ways to insert the spaces is 25 * 24 * 23 * 22 * 21 = 6375600.

Step 3: Multiply the number of full permutations by the number of ways to insert the spaces to get the total number of 6-word sentences. 403291461126605635584000000 * 6375600 = 2571861957619336464277760000000.

For more similar questions on permutations:

brainly.com/question/1216161

#SPJ11

The nth derivative of y = sin(x)cos(x) is dⁿy/dxⁿ = (-1)^(n+1) * n! * sin(x)cos(x)

To find the nth derivative of y = sin(x)cos(x), we can use the product rule and the chain rule repeatedly. Let's go through the process step by step.

The given function is y = sin(x)cos(x).

First, let's find the first derivative (n = 1):

dy/dx = (cos(x)cos(x)) + (sin(x)(-sin(x)))

= cos^2(x) - sin^2(x)

Now, let's find the second derivative (n = 2):

d²y/dx² = d/dx[cos^2(x) - sin^2(x)]

= d/dx[cos^2(x)] - d/dx[sin^2(x)]

To find the derivative of cos^2(x), we can apply the chain rule:

d/dx[cos^2(x)] = 2cos(x)(-sin(x)) = -2sin(x)cos(x)

To find the derivative of sin^2(x), we can again apply the chain rule:

d/dx[sin^2(x)] = 2sin(x)cos(x)

Substituting these results back into the second derivative expression:

d²y/dx² = -2sin(x)cos(x) - 2sin(x)cos(x)

= -4sin(x)cos(x)

We can continue this process to find higher-order derivatives by differentiating the expression obtained for the (n-1)th derivative.

In summary, the nth derivative of y = sin(x)cos(x) is given by:

dⁿy/dxⁿ = (-1)^(n+1) * n! * sin(x)cos(x)

Note that the alternating signs (-1)^(n+1) arise due to the repeated application of the product rule.

Learn more about derivative at https://brainly.com/question/32525596

#SPJ11

The problem is related to calculating the probability that the station will not run out of gasoline before the order arrives. Given, the mean, µ = 930 gallons and the standard deviation, σ = 140 gallons. The inventory is 1,200 gallons which is also known as the reorder point. The waiting period to receive inventory is called lead time. The demand during the lead-time period for regular gasoline, as measured in gallons, follows the normal distribution.

Using the formula P(z > (R - µ)/σ) = P(z > (1200 - 930)/140) = P(z > 1.93), we get the value of P(z > 1.93) as 0.027 by using the standard normal distribution table.

Therefore, if P(z > (R - µ)/σ) = 0.027, then P(z ≤ (R - µ)/σ) = 0.973. Thus, the probability that the station will not run out of gasoline before the order arrives is 0.973 or 97.3%. Hence, the correct option is 97.3% or 0.973.

Know more about probability here:

https://brainly.com/question/31828911

#SPJ11

Answer:

1) when tomato patch is 6.5 feet the area is 191.75 sq.ft

2)  when tomato patch is 7 feet the area is 217 sq.ft

3) when area is 338 sq.ft the tomato patch is 9.0778 feet

4) when area is 147.25 sq.ft the tomato patch is 5.543799 feet

Step-by-step explanation:

The given equation is  :

3x^2 + 10x

Length of Tomato (in feet)                                       x,  6.5   ,  x   ,     7

Patch Area of Vegetable Garden (in square feet) 338, x , 147.25, x

So we can find the missing terms with the help of the equation 3x^2 + 10x

Putting the values of x from the length of the tomato patch

1)  3x^2 + 10x= 3(6.5)²+ 10 (6.5)=126.75+ 65= 191.75 square feet

2) 3x^2 + 10x= 3(7)² +10 (7)= 147+70= 217 square feet

So the area of  her vegetable garden for a variety of  lengths of the tomato patch= 6.5 feet is 191.75  square feet

and for 7 feet is 217 square feet

Similarly we can find the length of the tomato patch from the area by again using the given equation  3x^2 + 10x

So when area = 338 square feet

The equation becomes  

3x^2 + 10x= 338

Rearranging it :     3x^2 + 10x-338 =0

This is a quadratic equation and can be solved with the help of the formula.

Here a= 3, b= 10 and c= -338

x = -b±√b²- 4ac/2a

Putting the values of a,b,c we get

x= -10±√100+ 4056/6

x= -10± 64.467/6

x= 54.467/6 or -74.467/6   we ignore the negative value because the garden cannot have the negative area.

x= 9.0778 feet

Similarly repeating the same process would give

So when area = 147.25 square feet

The equation becomes  

3x^2 + 10x= 147.25

Rearranging it :     3x^2 + 10x-147.25 =0

This is a quadratic equation and can be solved with the help of the formula.

Here a= 3, b= 10 and c= - 147.25

x = -b±√b²- 4ac/2a

Putting the values of a,b,c we get

x= -10±√100+ 1767/6

x= -10± 43.208/6

x= 33.208/6 or -53.208/6  we ignore the negative value because the garden cannot have the negative area.

x= 5.543799 feet

Answer:

1  12/35

Step-by-step explanation:

If you add the fractions together you get 1  12/35.

The graph will be steeper than the parent function √x due to the vertical stretch by a factor of 5. Additionally, the entire graph will be shifted 5 units upward. The sketch will have a smooth curve passing through the points (0, 0), (1, 5), (4, 10), and (9, 15), and it will continue to rise as x increases further.

(a) The parent function f related to g(x) = 5√x is f(x) = √x.

(b) The sequence of transformations from f to g is:

Vertical stretch by a factor of 5: This stretches the graph vertically, making it taller.

Vertical shift of 5 units upward: This shifts the entire graph 5 units higher.

No horizontal shift: There is no horizontal shift in this case.

No reflection in the x-axis: There is no reflection in the x-axis.

No vertical shrink: Instead, there is a vertical stretch.

Therefore, the correct transformations are:

Vertical stretch

Vertical shift of 5 units upward

(c) To sketch the graph of g, we can start by plotting a few points. Since g(x) = 5√x, we can choose x-values and evaluate the corresponding y-values.

Let's select some x-values and calculate the corresponding y-values:

For x = 0, g(0) = 5√0 = 0.

For x = 1, g(1) = 5√1 = 5.

For x = 4, g(4) = 5√4 = 10.

For x = 9, g(9) = 5√9 = 15.

Using these points, we can sketch the graph of g(x) on a coordinate system. Starting at the point (0, 0), the graph will gradually rise as x increases. The graph will be steeper than the parent function √x due to the vertical stretch by a factor of 5. Additionally, the entire graph will be shifted 5 units upward.

The sketch will have a smooth curve passing through the points (0, 0), (1, 5), (4, 10), and (9, 15), and it will continue to rise as x increases further.

Learn more about parent function here

https://brainly.com/question/19043302

#SPJ11

Triangle with sides AB = 8cm , CA = 5cm , BC = 7cm and AB = 7cm , BC = 10cm , CA = 8cm can construct a Triangle.

Condition : For forming the triangle, the sum of two sides must be greater than the third side.

a.  AB = 4cm, CA = 3cm, BC = 10cm

   CA+BC=AB

   3+1=4

   4=4

Therefore, it cannot form a triangle because it is not satisfying the condition.

b.  AB = 8cm , CA = 5cm , BC = 7cm

    AB+CA>BC

    AB+BC>CA

    CA+BC>AB

    Therefore, it can form a triangle because it satisfies the condition.

c.  AB = 7cm, BC = 10cm, CA = 8cm

   AB+BC>CA

   AB+CA>BC

   BC+BC>AB

  Therefore, it can form triangle because it satisfies the condition.

Learn more about Triangle construction here:

https://brainly.com/question/10984479

#SPJ4

The derivate of the logarithmic function is :

f'(x) = [(4*x^3 + 2*e^2x)/(x^4 + e^2x)]

Remember that for the natural logarithm g(x) = ln(x), we have:

dg/dx = 1/x

Here we have the function:

f(x) = ln(x^4 + e^2x).

The derivate will be one over the argument (for what we wrote above) times the derivate of the argument, we will get:

f'(x) = [1/(x^4 + e^2x)]*(4*x^3 + 2*e^2x)

Learn more about logarithmic functions:

https://brainly.com/question/13473114

#SPJ1

The graph of N(t) = 75t + 120 is a straight line with a positive slope of 75. It intersects the y-axis at (0, 120) and has a y-intercept of -8/5. As t approaches infinity, N(t) increases without bound, indicating a positive relationship between the number of days of training and the average number of components assembled per day.

To sketch the graph of N(t) = 75t + 120, we can plot points on the coordinate plane by substituting different values of t into the equation.

For example, when t = 0, N(0) = 75(0) + 120 = 120. So, we have the point (0, 120).

When t = 1, N(1) = 75(1) + 120 = 195. So, we have the point (1, 195).

We can continue to calculate more points using different values of t.

The intercept is when N(t) = 0:

0 = 75t + 120

-120 = 75t

t = -120/75

t = -8/5

So, we have the intercept (0, -8/5).

To find the asymptote, we need to check what happens to N(t) as t approaches infinity. As t becomes larger and larger, the constant term 120 becomes less significant compared to the term 75t. Therefore, as t approaches infinity, N(t) approaches infinity as well.

In practical terms, this means that as the number of days of training (t) increases, the average number of components assembled (N) per day also increases. However, it is important to note that this is based on past records and the actual performance of new employees may vary. The equation provides an average trend and does not account for individual variations or other factors that may affect productivity.

To know more about coordinate plane refer here :    

https://brainly.com/question/13611766#

#SPJ11      

Answer:

Hi... Do this for prove that

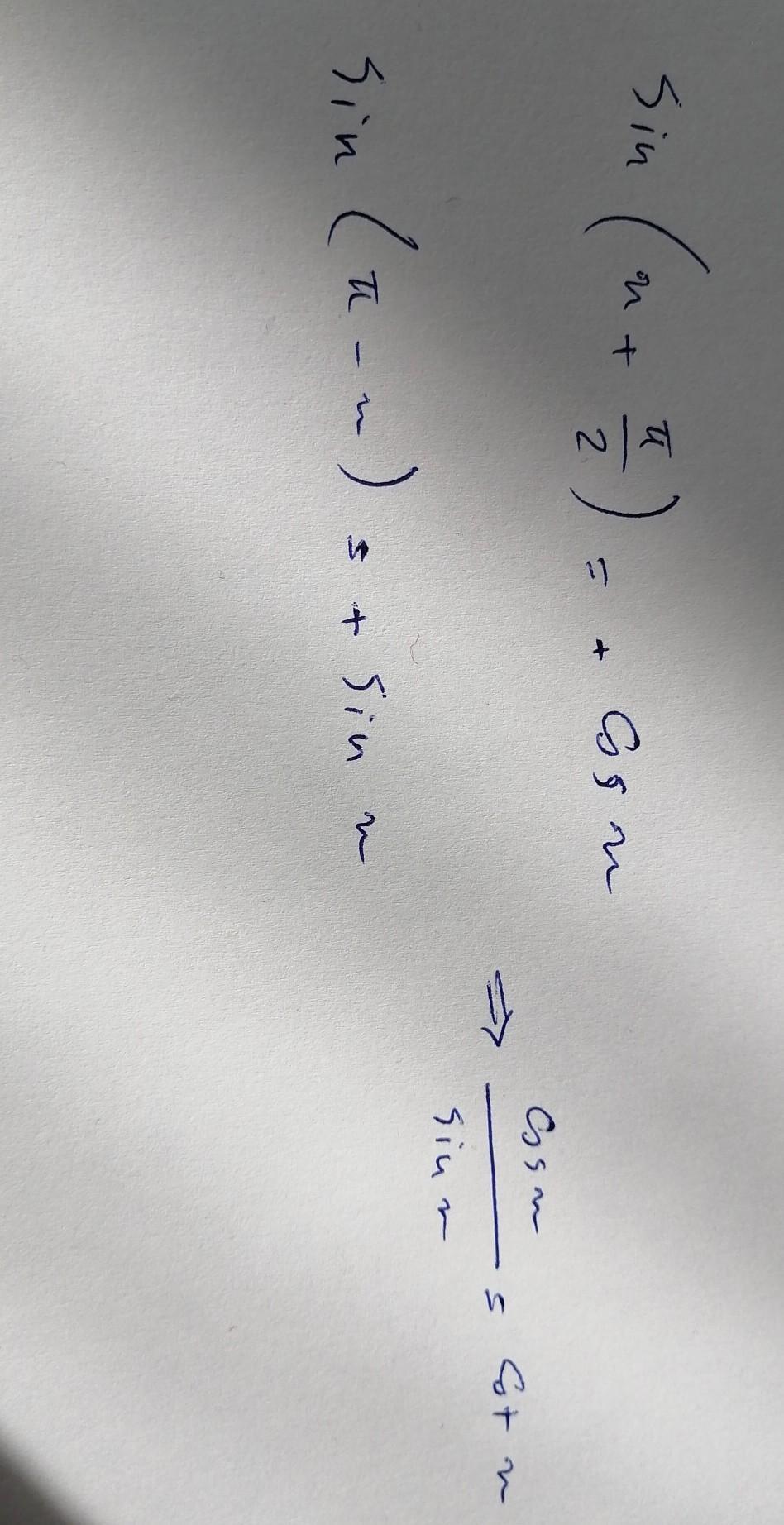
Answer:

Step-by-step explanation: