Black walnut trees contain chemicals that inhibit the growth of other plants. In a simple experiment to test whether this is true, you grow several tomato plants in soil with and without decomposing leaves from a black walnut tree. You collect data on plant height as a measure of growth. In this experiment, __________ is the independent variable, __________ is the dependent variable, and __________ is the control.
Answers
Answer:
Height of tomato plant is the dependent variable
Presence of walnut leaves in the soil is the independent variable
Tomato plants grown without walnut leaves is the control
Step-by-step explanation:
An independent variable is the variable in an experiment that can be altered to test for a certain result. It is independent, or does not change with change in other factors in the experiment. In this case, the presence or absence, or quantity of walnut available in the soil is the independent variable in the experiment.
A dependent variable varies, and depends on the independent variable. It is what is measured in the experiment. In this case, the height of the tomato plants is the dependent variable that depends on the presence, absence or quantity of walnut in the soil.
A control in an experiment, is a replicate experiment, that is manipulated in order to be able to test a single variable at a time. Controls are variables are held constant so as to minimize their effect on the system under study. In this case, some of the tomato plants are planted without walnut in the soil, to test the effect of the absence of the walnut in the soil.
Related Questions
Solve.
X = -7
4x - 4y = 12
(x,y)
Answers
Answer:
(-7, -10)
\(x=-7\\y=-10\)
Step-by-step explanation:
\(4x-4y=12\)
Substitute x for -7.
\(4(-7)-4y=12\)
Multiply 4 by -7.
\(-28-4y=12\)
Add 28 on both sides.
\(-4y=40\)
Divide -4 on both sides.
\(y=-10\)
The Zippy Lube business where you work printed coupons offering $4.00 off any oil change this month. An oil change costs $19.98 and a new oil filter costs $4.15. A customer comes in with a coupon and has you change the oil and filter. Before adding the tax, how much should you charge the customer?
Answers
A 33 33 -ft ladder leans against a building so that the angle between the ground and the ladder is .
Answers
Question:
A 33 foot ladder leans against a building so that the angle between the ground and the ladder is 75º. How high does the ladder reach up the side of the building?
Round to 2 decimal places feet.
Answer:
\(H = 31.88\)
Step-by-step explanation:
The question is illustrated using the attachment as a sketch.
We have that
\(Ladder = 33ft\)
\(\theta = 75\)
Required
Determine how high the ladder is to the building
Represent the length of the ladder with L and how high the ladder is on the building with H.
The relationship between L, H and \(\theta\) is"
\(Sin\theta = \frac{H}{L}\)
Substitute values for L and \(\theta\\\)
\(Sin(75) = \frac{H}{33}\)
Make H the subject
\(H = 33 * Sin(75)\)
\(H = 33 * 0.9660\)
\(H = 31.88\)
Hence, the height to which the ladder reaches is approximately 31.88ft

Any help would be appreciated, No links please. Thank you

Answers
Answer:
C
Step-by-step explanation:
I already did this. ;)
I am stuck please help with this graph.
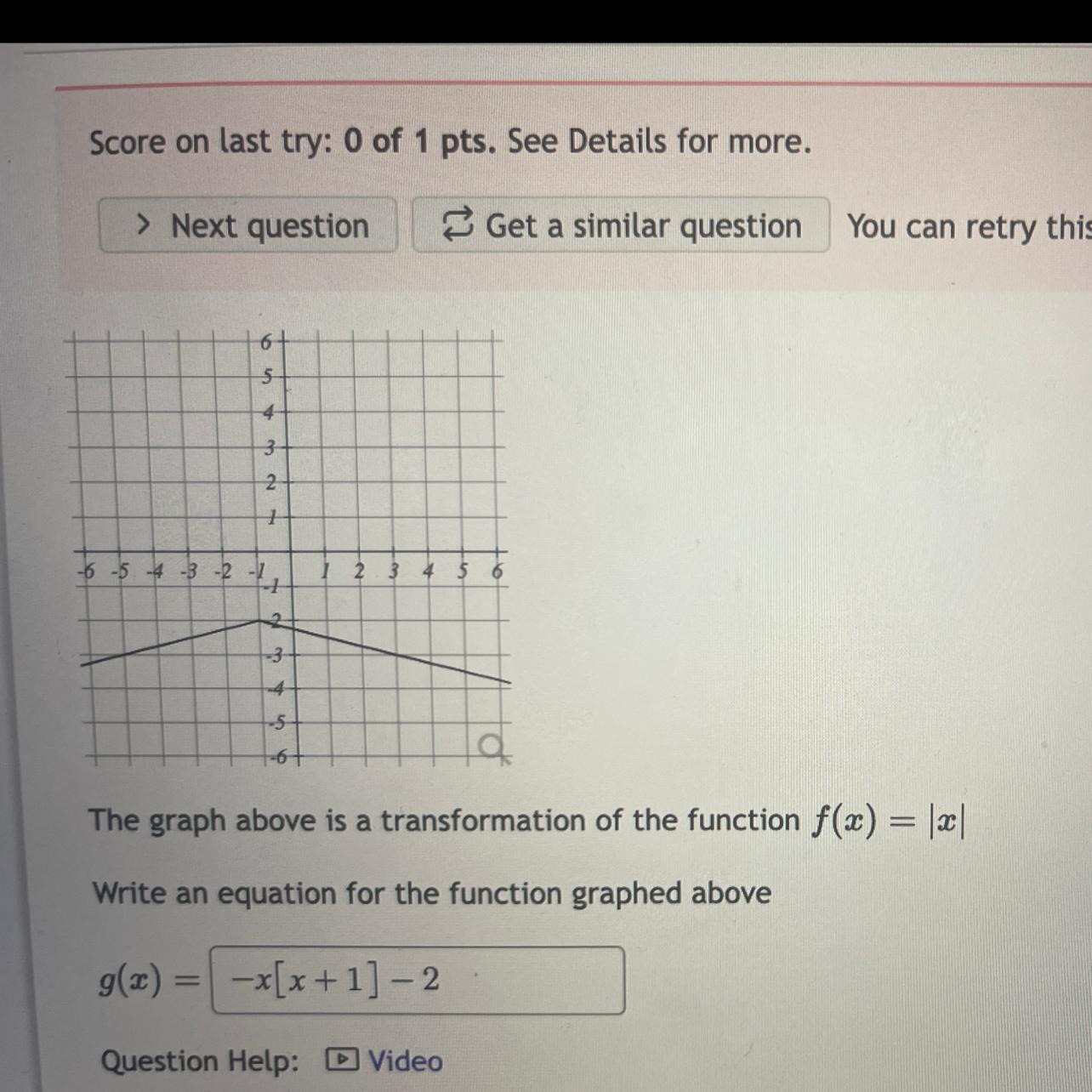
Answers
An equation for the function graphed above include the following: g(x) = -1/4|x + 1| - 2.
How to interpret and determine the equation of g(x)?By critically observing the graph of this absolute value function, we can reasonably infer and logically deduce that the parent absolute value function f(x) = |x| was vertically compressed by a factor of 1/4, reflected over the x-axis, followed by a vertical translation 2 units down, and then a horizontal translation to the left by 1 unit, in order to produce the transformed absolute value function as follows;
f(x) = |x|
y = A|x + B| + C
g(x) = -1/4|x + 1| - 2
In conclusion, the value of the variables A, B, and C are -1/4, 1, and 2 respectively.
Read more on absolute value function here: brainly.com/question/28308900
#SPJ1
The sum of four times a number and 3 is -13. Find the number.
Answers
Answer:
x is equal to -4
Step-by-step explanation:
4x+3= -13
4x/4= -16/4
x= -4
Using lexicographic ordering of 5-tuples, select the two inequalities that are both correct. a. (3,1,10,17,2)<(3,1,10,20,1) (5,1,10,17,2)<(5,0,101,2,2) b. (3,1,10,17,2)>(3,1,10,20,1) (5,1,10,17,2)<(5,0,101,2,2) c. (3,1,10,17,2)<(3,1,10,20,1)
(5,1,10,17,2)>(5,0,101,2,2) d. (3,1,10,17,2)>(3,1,10,20,1) (5,1,10,17,2)>(5,0,101,2,2)
Answers
Using the lexicographic ordering 5 tuples we get that option b and d is correct.
The lexicographic ordering of 5-tuples means that we compare the elements of each tuple from left to right, and as soon as we find a pair of elements that differ, we say that the tuple with the smaller element is less than the other tuple.
Using this ordering, we can compare the given tuples as follows:
a. (3,1,10,17,2) < (3,1,10,20,1) is true because the fifth element of the first tuple (2) is smaller than the fifth element of the second tuple (1).
(5,1,10,17,2) < (5,0,101,2,2) is false because the second element of the first tuple (1) is greater than the second element of the second tuple (0).
Therefore, option (a) is not correct.
b. (3,1,10,17,2) > (3,1,10,20,1) is false because the fifth element of the first tuple (2) is smaller than the fifth element of the second tuple (1).
(5,1,10,17,2) < (5,0,101,2,2) is true because the second element of the first tuple (1) is smaller than the second element of the second tuple (0).
Therefore, option (b) is correct.
c. (3,1,10,17,2) < (3,1,10,20,1) is true because the fifth element of the first tuple (2) is smaller than the fifth element of the second tuple (1).
(5,1,10,17,2) > (5,0,101,2,2) is true because the second element of the first tuple (1) is greater than the second element of the second tuple (0).
Therefore, option (c) is not correct.
d. (3,1,10,17,2) > (3,1,10,20,1) is false because the fifth element of the first tuple (2) is smaller than the fifth element of the second tuple (1).
(5,1,10,17,2) > (5,0,101,2,2) is true because the second element of the first tuple (1) is greater than the second element of the second tuple (0).
Therefore, option (d) is correct.
So the correct answer is (b) and (d).
To learn more about lexicographic ordering click here
brainly.com/question/13106850
#SPJ4
It is question 16 pls help

Answers
Answer: yes it is 16 i did my work let me know if you want me to show my work
Step-by-step explanation:
help me solve this queston

Answers
TJohn's age is approximately 23.33 years, and Sharon's age is approximately 93.33 years.
And the correct graph is D.
To represent the given problem as a system of equations, we can use the following information:
John is 70 years younger than Sharon: j = s - 70
Sharon is 4 times as old as John: s = 4j
Let's plot the graph for this system of equations:
First, let's solve equation (2) for s:
s = 4j
Now substitute this value of s in equation (1):
j = s - 70
j = 4j - 70
3j = 70
j = 70/3
Substitute the value of j back into equation (2) to find s:
s = 4j
s = 4(70/3)
s = 280/3
The solution to the system of equations is j = 70/3 and s = 280/3
In the graph d, the solution to the system of equations is represented by the point (70/3, 280/3), which is approximately (23.33, 93.33) on the graph.
Therefore, John's age is approximately 23.33 years, and Sharon's age is approximately 93.33 years.
And the correct graph is D.
Learn more about system of equations click;
https://brainly.com/question/20067450
#SPJ1

What is the greatest common factor of 12,18,26
Answers
6. The base of a pyramid is a triangle whose base is 11 yards and height is 19
yards. Determine the volume of the pyramid, if its height is 7 yards. Round
your answer to two decimal places.
Answers
Because volume= lwh/3
What are the domain and range of the exponential decay function?
A) Domain: X < 3 Range: Y > 3
B) Domain: All real numbers; Range: y > 3
C) Domain: All real numbers; Range: All real numbers
D) Domain x > 3; Range: All real numbers

Answers
Answer:
B) Domain: All real numbers; Range: y > 3
Step-by-step explanation:
I. x can be any value in real number
but if you look at the graph, the y is near 3 but not 3
So y is more than 3 and x is all real number
When x is domain and y is renge.
That makes domain is real number and renge is more than 3.
Hope that help :)
54 ÷ 6 x (12-4) + 2 =
Answers
Answer:
3
Step-by-step explanation:
1. 54÷6 =9
2. (12-4)=8
3. 9-8 = 1
4. 1+2 = 3
5. I hope this helps it's pretty simple oh and 3 is your anansw.Also you can you your calculator
Answer:
a=72\(\frac{2}{3}\)
Step-by-step explanation:
56/6*(12-4)+2=n
56/6*8+2-2=n-2
56/6*8/8=(n-2)/8
x=9\(\frac{1}{3}\)
x=(n-2)/8
y=74\(\frac{2}{3}\)
y=n-2=a
a=72\(\frac{2}{3}\)
2.1(0.2x-1.4)=1.3(0.4x—3.5)
Pls help.
Answers
Answer:
x=161/10 =16.100
Step-by-step explanation:
Combine Like Terms
PLEASE FOLLOW ME
Answer:
hope it helps..
Step-by-step explanation:
Simplifying
2.1(0.2x + -1.4) = 1.3(0.4x + -3.5)
Reorder the terms:
2.1(-1.4 + 0.2x) = 1.3(0.4x + -3.5)
(-1.4 * 2.1 + 0.2x * 2.1) = 1.3(0.4x + -3.5)
(-2.94 + 0.42x) = 1.3(0.4x + -3.5)
Reorder the terms:
-2.94 + 0.42x = 1.3(-3.5 + 0.4x)
-2.94 + 0.42x = (-3.5 * 1.3 + 0.4x * 1.3)
-2.94 + 0.42x = (-4.55 + 0.52x)
Solving
-2.94 + 0.42x = -4.55 + 0.52x
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-0.52x' to each side of the equation.
-2.94 + 0.42x + -0.52x = -4.55 + 0.52x + -0.52x
Combine like terms: 0.42x + -0.52x = -0.1x
-2.94 + -0.1x = -4.55 + 0.52x + -0.52x
Combine like terms: 0.52x + -0.52x = 0.00
-2.94 + -0.1x = -4.55 + 0.00
-2.94 + -0.1x = -4.55
Add '2.94' to each side of the equation.
-2.94 + 2.94 + -0.1x = -4.55 + 2.94
Combine like terms: -2.94 + 2.94 = 0.00
0.00 + -0.1x = -4.55 + 2.94
-0.1x = -4.55 + 2.94
Combine like terms: -4.55 + 2.94 = -1.61
-0.1x = -1.61
Divide each side by '-0.1'.
x = 16.1
Simplifying
x = 16.1
the student government claims that 70% of all students favor an increase in student fees to buy indoor potted plants for the classrooms. a random sample of 12 students produced 2 in favor of the project.
(a) What is the probability that 2 or fewer in the sample will favor the project, assuming the student government's claim is correct? (Use 3 decimal places.) (b) Do the the data support the student government's claim, or does it seem that the percentage favoring the increase in fees is less than 70%? The data do not give us any indication that the percent favoring the increase in fees differs from 70%. The data seem to indicate that the percent favoring the increase in fees is greater than 70%. The data seem to indicate that the percent favoring the increase in fees is less than 70%. The data seem to indicate that the percent favoring the increase in fees is equal to 70%.
Answers
The probability that 2 or fewer in the sample will favor the project is 4.368 × 10⁻⁶ and Also The data seem to indicate that the percent favoring the increase in fees is less than 70%
According to the question,
It is given that according to the student's government
The probability that number of students in favor of increment in fees : p = 0.70
The probability that number of students against the increment : q = 0.30
Sample Size : n = 12
Number of students follows Binomial distribution
(a) We have to find the probability that 2 or fewer in the sample will favor the project
P( x ≤ 2) = P(0) + P(1) + P(2)
As we know ,
P(x) = ⁿCₓpˣq⁽ⁿ⁻ˣ⁾
=> P( x ≤ 2) = ¹²C₀p⁰q¹² + ¹²C₁p¹q¹¹ + ¹²C₂p²q¹⁰
=> P( x ≤ 2) = 1×(0.30)¹² + 12×(0.70)(0.30)¹¹ + 12×11/2 × (0.70)²(0.30)¹⁰
=> P( x ≤ 2) = (0.30)¹⁰ [ 0.09 + 0.21 + 0.48]
=> P( x ≤ 2) = 5.9×10⁻⁶[0.78]
=> P( x ≤ 2) = 4.368 × 10⁻⁶
Which is very close to zero
(b) The data doesn't support the student government claim.
The data seem to indicate that the percent favoring the increase in fees is less than 70%.
To know more about Binomial distribution here
https://brainly.com/question/29137961
#SPJ4
if y is directly porportional to x^2 and the difference in the values of y when x=1 and x=3 is 32, find the value of y when x=-2
Answers
Answer:
Step-by-step explanation:
y=kx²
y₁=k(1)²=k
y₃=k(3)²=9k
y₁-y₃=k-9k=32
-8k=32
k=-4
y=-4x²
y₋₂=-4(-2)²=-16
Help please if you can I beg
Answers
Subtract to find the difference in calories:
150-78 = 72
divide the difference by 150:
72/150 = 0.48
Multiply by 100 to get the percent:
0.48 x 100 = 48%
Answer: 48 %
Answer:
first of all subtract as given in question
158-78
after that divide the difference by 150
72/150=0.48
now at last multiply it with 100=0.48×100=48
Regs.
Spinner A and Spinner B below are each to be spun once.
0 18
O 12
6
Spinner A
5
2
4
00
D
3
20 of 21
If the pointer cannot land on a line, how many different outcomes of a number and a color are possible?
v
Spinner B
Yellow
Brown
12 13
Red
Answers
Answer:
Step-by-step explanation:
Regs.
Spinner A and Spinner B below are each to be spun once.
0 18
O 12
6
Spinner A
5
2
4
00
Which two expressions are equal given r=9?
a. r+20
b. 2×r+10
c. 4×r−10
e. 3×r+1
Answers
Answer:
2×r+10 and 3×r+1
Step-by-step explanation:
a. 9+20= 29
b. 2×9+10= 18+10 = 28
c. 4x9-10 = 36-10 =26
e. 3×9+1 = 27 +1 = 28
the correct answer are 2×r+10 and 3×r+1
In 1990, a total of $641 billion was spent on food and drinks in a particular country. In 2003, the total spent was $1016 billion.
(a) Find the equation of the exponential function that can be used to model the total 7 spent (in billions of dollars) on food and drinks in this country as a
function of the number of years t since 1990. (Round your decimal value to four decimal places.)
x
T=
(b) Use your model to predict the amount spent (in billions of dollars) in 2000. (Round your answer to the nearest integer.)
billion dollars
(c) What is your prediction for the total sales of food and drink (in billions of dollars) in 2018? (Round your answer to the nearest Integer.)
billion dollars
(d) Estimate when the total sales will reach $2 trillion if this exponential trend continues. (Round your answer to two decimal places.)
t=
Answers
Part(a),
The exponential function that models the total spent on food and drinks as a function of the number of years since 1990 is:
\(T(x) = 641 \times ((\dfrac{1016}{641})^{(\frac{1}{13}))^x\)
Part(b),
The predicted amount spent in 2000 is 964 billion dollars (rounded to the nearest integer).
Part(c),
The predicted total sales of food and drink in 2018 is 1756 billion dollars
Part(d),
If the exponential trend continues, the total sales will reach 2 trillion dollars approximately 32.72 years after 1990, which is around the year 2022.
(a) To model the total spent on food and drinks as an exponential function of the number of years since 1990, we can use the general form of an exponential function:
\(T = a \times b^t\)
where T is the total spent in billions of dollars, t is the number of years since 1990, a is the initial amount spent in 1990, and b is the growth factor or base of the exponential function.
Using the given information, we can set up two equations:
T(0) = 641 (total spent in 1990)
T(13) = 1016 (total spent in 2003, which is 13 years after 1990)
Substituting these values into the exponential function, we get:
\(641 = a \timrd b^0\) => a = 641
\(1016 = a b^{13\) => \(b = (\dfrac{1016}{641})^{\frac{1}{13}\)
Therefore, the exponential function that models the total spent on food and drinks as a function of the number of years since 1990 is:
\(T(x) = 641 \times ((\dfrac{1016}{641})^{(\frac{1}{13})^x\)
(b) To predict the amount spent in 2000, we need to substitute t = 10 (since 2000 is 10 years after 1990) into the exponential function:
\(T(10) = 641 \times ((\dfrac{1016}{641})^{(\frac{1}{13}))^{10\) ≈ 964
Therefore, the predicted amount spent in 2000 is 964 billion dollars (rounded to the nearest integer).
(c) To predict the total sales of food and drink in 2018, we need to substitute t = 28 (since 2018 is 28 years after 1990) into the exponential function:
\(T(28) = 641 \times ((\dfrac{1016}{641})^{(\frac{1}{13}))^{28\) ≈ 1756
Therefore, the predicted total sales of food and drink in 2018 is 1756 billion dollars (rounded to the nearest integer).
(d) To estimate when the total sales will reach 2 trillion dollars, we need to solve for t in the exponential function when T(t) = 2000 (since 2 trillion dollars is equivalent to 2000 billion dollars):
\(2000 = 641 \times ((\dfrac{1016}{641})^{(\frac{1}{13}))^t\)
\(ln(\dfrac{2000}{641}) = t \times ln((\dfrac{1016}{641})^{(\frac{1}{13})\)
\(t = \dfrac{ln(\dfrac{2000}{641})} { ln((\dfrac{1016}{641})^{(\frac{1}{13})) }}\)
t = 32.72
Therefore, if the exponential trend continues, the total sales will reach 2 trillion dollars approximately 32.72 years after 1990, which is around the year 2022.
To know more about exponential function follow
https://brainly.com/question/31295284
#SPJ1
Consider the function below, which has a relative minimum located at (-3, -18) and a relative maximum located at 1/3, 14/27). f(x) = -x3 - 4x2 + 3x. Select all ordered pairs in the table which are located where the graph of f(x) is decreasing: Ordered pairs: (-1, -6), (2, -18), (0, 0),(1 , -2), (-3 , -18), (-4. , -12)
Answers
The ordered pairs (-1, -6), (2, -18), (0, 0), and (-4, -12) do not correspond to the intervals where the graph of f(x) is decreasing. The pairs (1, -2) and (-3, -18) are the correct ones.
To determine where the graph of f(x) is decreasing, we need to examine the intervals where the function's derivative is negative. The derivative of f(x) is given by f'(x) = -3x^2 - 8x + 3.
Now, let's evaluate f'(x) for each of the given x-values:
f'(-1) = -3(-1)^2 - 8(-1) + 3 = -3 + 8 + 3 = 8
f'(2) = -3(2)^2 - 8(2) + 3 = -12 - 16 + 3 = -25
f'(0) = -3(0)^2 - 8(0) + 3 = 3
f'(1) = -3(1)^2 - 8(1) + 3 = -3 - 8 + 3 = -8
f'(-3) = -3(-3)^2 - 8(-3) + 3 = -27 + 24 + 3 = 0
f'(-4) = -3(-4)^2 - 8(-4) + 3 = -48 + 32 + 3 = -13
From the values above, we can determine the intervals where f(x) is decreasing:
f(x) is decreasing for x in the interval (-∞, -3).
f(x) is decreasing for x in the interval (1, 2).
Now let's check the ordered pairs in the table:
(-1, -6): Not in a decreasing interval.
(2, -18): Not in a decreasing interval.
(0, 0): Not in a decreasing interval.
(1, -2): In a decreasing interval.
(-3, -18): In a decreasing interval.
(-4, -12): Not in a decreasing interval.
Therefore, the ordered pairs (-1, -6), (2, -18), (0, 0), and (-4, -12) are not located in the intervals where the graph of f(x) is decreasing. The correct answer is: (1, -2), (-3, -18).
For more question on intervals visit:
https://brainly.com/question/30460486
#SPJ8
Note the complete and the correct question is
Q- Consider the function below, which has a relative minimum located at (-3, -18) and a relative maximum located at 1/3, 14/27).
\(f(x) = -x^3 - 4x^2 + 3x\).
Select all ordered pairs in the table which are located where the graph of f(x) is decreasing: Ordered pairs: (-1, -6), (2, -18), (0, 0),(1 , -2), (-3 , -18), (-4. , -12)
Given the polynomial 9x2y6 − 25x4y8, rewrite as a product of polynomials.
(9xy3 − 25x2y4)(xy3 + x2y4)
(9xy3 − 25x2y4)(xy3 − x2y4)
(3xy3 − 5x2y4)(3xy3 + 5x2y4)
(3xy3 − 5x2y4)(3xy3 − 5x2y4)
Answers
Answer:
Option 3
(3xy³ + 5x²y⁴) (3xy³ - 5x²y⁴)
Step-by-step explanation:
Factorize polynomials:
Use exponent law:
\(\boxed{\bf a^{m*n}=(a^m)^n} \ & \\\\\boxed{\bf a^m * b^m = (a*b)^m}\)
9x²y⁶ = 3²* x² * y³*² = 3² * x² * (y³)² = (3xy³)²
25x⁴y⁸ = 5² * x²*² * y⁴*² = 5² * (x²)² * (y⁴)² = (5x²y⁴)²
Now use the identity: a² - b² = (a +b) (a -b)
Here, a = 3xy³ & b = 5x²y⁴
9x²y⁶ - 25x⁴y⁸ = 3²x²(y³)² - 5²(x²)² (y⁴)²
= (3xy³)² - (5x²y⁴)²
= (3xy³ + 5x²y⁴) (3xy³ - 5x²y⁴)
Find the principal invested if $549 interest was earned in 8 years at an interest rate of 9%
Answers
The value of the principal invested is $762. 5
How to determine the principal amountThe formula for calculating simple interest is expressed as;
I = PRT/100
Such that the parameters of the formula are represented as;
I is the simple interest.P is the principal amount.R is the rate of the interest.T is the time in years taken.Now, substitute the values into the equation, we have;
$549 = P × 9 × 8/100
Multiply the values
$549 = 72P/100
cross multiply the values
$549 × 100 = 72P
Multiply the values
72P = 54900
Divide both sides by the coefficient of P
P = $762. 5
Learn about simple interest at: https://brainly.com/question/25793394
#SPJ1
(Irrational Numbers MC)
Approximate -10 + √30 to the nearest tenth. HELP PLS
Answers
-10 + 5.47722~
=4.523~
round to nearest tenth = 4.5
Answer:
-4.5
Step-by-step explanation:
\(\sqrt{30}\) is approximately 5.47722557505. You can find this number with a calculator.
-10 + 5.47722557505 = -4.52277442495
To add a negative and a positive number, you subtract the absolute values and take the sign of the number that has the larger absolute value. Absolute value just means thinking of both numbers as positive numbers.
Helping in the name of Jesus.
Draw the net and calculate the surface area .

Answers
Hello!
surface area
= 2(4 x 2) + 2(12 x 4) + 2(12 x 2)
= 160cm²
Rewriting 3x^2=6x and solving with rewritten
Answers
Answer:
x = 0 , x = 2
Step-by-step explanation:
3x² = 6x ( subtract 6x from both sides )
3x² - 6x = 0 ← factor out 3x from each term
3x(x - 2) = 0
equate each factor to zero and solve for x
3x = 0 ⇒ x = 0
x - 2 = 0 ( add 2 to both sides )
x = 2
solutions are x = 0 , x = 2
Identify the solution of the system graphed below. Choose an answer below.
(−2, −1)
This system has infinitely many solutions.
(−1, −1)
This system has no solutions

Answers
Answer:
Solution: (-1, -1)
Step-by-step explanation:
When a system of equations is graphed, the solution to the system is the intersection point of the two equations.Thus, the solution to the system is (-1, -1) as this is the point where the two lines intersect.
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
Answers
Answer:
53\(x_{123}\) == 134 cf
Step-by-step explanation:
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
The height of the building is approximately 78.63 meters.
The following is a step-by-step explanation of how to solve the problem. We'll need to use some trigonometric concepts and formulas to find the solution.
Draw a diagram of the situation described in the problem to get a better understanding of the problem. The diagram would have a right-angled triangle with angle of elevation of 66° at the bottom left vertex and another angle of elevation of 53° at the bottom right vertex. The object on top of the building is at the vertex of the triangle. Point M and I on the diagram are points on the horizontal line of sight and on the ground respectively. We can label the diagram with the following values:Angle of elevation from point A = 66°Angle of elevation from point P = 53° Length of line segment AM = h Length of line segment MP = x Length of line segment IP = y Length of line segment MT = 50m. We'll use these values to calculate the length of h, which is the height of the building.Use the tangent ratio to find x:tan 66° = h / x => x = h / tan 66°. Use the tangent ratio to find y:tan 53° = h / y => y = h / tan 53°.We know that x + y = 50, so substituting the expressions for x and y from step 3 gives:h / tan 66° + h / tan 53° = 50h = 50 tan 66° tan 53° / (tan 53° + tan 66°) ≈ 78.63 m.Therefore, the height of the building is approximately 78.63 meters.
For more such questions on height, click on:
https://brainly.com/question/28122539
#SPJ8
If one cubic foot of water weighs 62 1/2 pounds how much do 3 1/5 cubic feet of water weighs?
Answers
Answer:
3 1/5 cubic feet of water weighs 200 pounds
Step-by-step explanation:
1. Take 62 1/2 into decimal form: 62 1/2 = 62.5
2. Take 3 1/5 into decimal form: 3 1/5 = 3.2
3. Multiple 62.5 by 3.2: 62.5 x 3.2 = 200
The answer is 200 pounds.
if you could fly and every hour u loose 30 feathers in 14 days how many feathers did you loose?
Answers
The total number of feathers lost in 14 days if you lose 30 feathers every hour is 10,080 feathers.
How many feathers will you loose?Feathers lost every hour = 30 feathers
How many feathers is lost in 14 days?
1 day = 24 hours
14 days = 24 × 14
= 336 hours
Total number of feathers lost in 14 days = Feathers lost every hour × number of hours in 14 days
= 30 × 336
= 10,080 feathers
Therefore, the total number of feathers lost in 14 days is 10,080 feathers
Read more on multiplications:
https://brainly.com/question/10873737
#SPJ1