Bob went out to dinner and paid a 15% tip on a $20 meal? How much is the total bill?
Answers
Answer:
23
Step-by-step explanation:
15% of 20 = 3 then add the 3 to the 20 to get 23
23Answer:
Step-by-step explanation:
15/100*20 = 3
20+3 = 23
Related Questions
Data table Activity Optimistic START 0 ABCDEFGHIK А J L FINISH 605 2607NTO TO 2-253 N N N M - NO 15 3 1 1 1 Time Estimates (days) Most Likely 0 0 10 1 20 10 2 2 2 3 1 Print Pessimisitic 0 OANAN www�
Answers
Answer:
This is gebber gabber but yes
Step-by-step explanation:
Peter creates balloon animals for different events. He has 644 balloons. He wants to use
the same number of balloons for each of 28 events. How many balloons can Peter use at
each event?
Answers
Answer:
He uses 23 balloons for each of the 28 events.
Step-by-step explanation:
Answer:
23
Step-by-step explanation:
I divided 644 by 28. There are 644 balloons and you want to split
(divide) into the same number of balloons with none left over. Look for those key words to tell you what type of math your doing. Hope this helps!
During a charity drive, the senior class raised $85 more than twice the amount raised by the freshman class. The senior class raised $555. How much did the freshman class raise?
Answers
Answer:
235$
Step-by-step explanation:
85+2x=555
-85 -85
2x=470
2x/2x 460/2x
235
so the freshman class raised 235$
A jogger runs directly east for 5 km, then turns and goes northwest for 6 km. He then travels directly south for 3 km. How far is he from the starting point? ( km) Tries 1/12 Previous Tries In what direction is he from the starting point(measured as an angle counterwise from the east axis, units are deg)? (Northwest is the direction lying exactly half way between north and west.) Tries 0/12
Answers
The jogger is 3 km away from the starting point and is located at an angle of 45 degrees counter-clockwise from the east axis.
To calculate the distance from the starting point, we can use the Pythagorean theorem. The jogger first runs 5 km east, then 6 km northwest, and finally 3 km south.
The distance traveled east and west cancels out, as they are in opposite directions. So we only need to consider the north-south distance.
The north-south distance is the sum of the distances traveled north (0 km) and south (3 km), which gives us a total distance of 3 km.
Therefore, the jogger is 3 km away from the starting point.
To determine the direction from the starting point, we can use trigonometry. We can consider the east direction as 0 degrees, and measure angles counter-clockwise from the east axis.
Since the jogger traveled northwest, which is halfway between north and west, the angle from the east axis would be 45 degrees (45°).
To learn more about angle here:
https://brainly.com/question/33000969
#SPJ4
a spherical snowball is melting in such a way that its radius is decreasing at a rate of 0.3 cm/min. at what rate is the volume of the snowball decreasing when the radius is 15 cm. (note the answer is a positive number).
Answers
So, the volume of the snowball is decreasing at a rate of approximately 2,130.51 cm^3/min when the radius is 15 cm.
When dealing with problems involving rates and volumes, it's important to remember the formula for the volume of a sphere, which is V = (4/3)πr^3.
Now, we know that the radius of the snowball is decreasing at a rate of 0.3 cm/min, which means dr/dt = -0.3 cm/min (the negative sign indicates that the radius is decreasing). We want to find the rate at which the volume of the snowball is decreasing, or dV/dt.
To do this, we'll need to use the chain rule of differentiation. That means we'll need to differentiate the volume formula with respect to time:
dV/dt = d/dt[(4/3)πr^3]
= 4πr^2 (dr/dt)
= 4π(15)^2 (-0.3)
= -678π cm^3/min
Note that we plugged in r = 15 cm because that's the radius when we're trying to find the rate of volume change. Also, since we're looking for a positive rate, we'll take the absolute value of the answer:
|dV/dt| = 678π cm^3/min
So, the volume of the snowball is decreasing at a rate of approximately 2,130.51 cm^3/min when the radius is 15 cm. I hope that helps! Let me know if you have any other questions.
To know more about radius visit:
https://brainly.com/question/13449316
#SPJ11
Hemoglobin
Level Person's Age
Less than
25 years 25-35 years Above 35 years Total
Less than 9 21 32 76 129
Between 9 and 11 49 52
Above 11 69
40
Total 139 128 162 429
10
Select the correct answer.
What is the probability that a person who is older than 35 years has a hemoglobin level between 9 and 11?
A.
0.257
B.
0.284
C.
0.312
D.
0.356
E.
0.548
Answers
P(hemoglobin level between 9 and 11 | age > 35) = 52/162
Simplifying this fraction gives:
P(hemoglobin level between 9 and 11 | age > 35) = 0.321
Therefore, the correct answer is option C, 0.312 (rounded to three decimal places).
A box in the shape of a rectangular prism has a length of 358 inches in width of two 1/2 inches and a height of 4 inches. What is the volume of the box?
Answers
The volume of the box in shape of a rectangular prism is solved to be
716 inches³
What is a rectangular prism?Three-dimensional object with six faces is called a rectangular prism (two at the top and bottom and four are lateral faces).
The prism has rectangular-shaped faces on each side. As a result, there are three sets of matching faces in this picture. Rectangular prisms are sometimes known as cuboids due to their shape.
In the given problem the formula used for volume of prism is
= length * width * height
= 358 * 1/2 * 4
= 716 inches³
The prism has a volume of 716 inches³
Learn more about prism at:
https://brainly.com/question/23963432
#SPJ1
The volume of the rectangular prism with a length of 358 inches, width of 1/2 inches and a height of 4 inches is 716 in³.
What is the volume of the rectangular prism?The volume of a rectangular prism is expressed as;
V = w × h × l
Where w is width, h is height and l is length.
Given that;
Length l = 358 inWidth w = 1/2 inHeight h = 4 inPlug the given values into the above formula and simplify.
V = w × h × l
V = 1/2 in × 4 in × 358 in
V = 716 in³
Therefore, the volume of the box is 716 in³.
Learn more about volume of prism here: https://brainly.com/question/23963432
#SPJ1
Jake earned $1.155 in interest from his savings account over the last 5 years. The account has an annual rate of 1.25% how much did jake originally deposit in his account as his principal?
Answers
9514 1404 393
Answer:
$18.48
Step-by-step explanation:
If we assume the account earned simple interest, the amount is given by the formula ...
I = Prt . . . . interest on principal P at annual rate r for t years
1.155 = P·0.0125·5
P = 1.155/0.0625 = 18.48
Jake initially deposited $18.48 as his principal.
_____
Additional comment
The amount $1.155 is an unusual specification for an amount of money. If you mean $1,155.00, then the principal amount is likewise multiplied by 1000: $18,480.
A carpenter needs to cut 24-inch pieces of wood from a board that is 17 feet in length. What is the greatest number of 24-inch pieces the carpenter can cut from 6 of these boards of wood?
Answers
The greatest number of 24 inch pieces the carpenter can cut from 6 boards of wood is 51.
How to find the greatest number of 24 inches pieces that can be cut from the board?A carpenter needs to cut 24-inch pieces of wood from a board that is 17 feet in length.
Therefore, the greatest number of 24 inches pieces the carpenter can cut from 6 of these boards of wood can be calculated as follows:
let's convert from feet to inches.
17 feet = 204 inches
1 board = 204 inches
6 board = ?
cross multiply
length of 6 board = 204 × 6
length of 6 board = 1224 inches
Hence,
greatest number of 24 inch that can be cut from 6 boards = 1224 / 24
greatest number of 24 inch that can be cut from 6 boards = 51
learn more on length here: https://brainly.com/question/21415862
#SPJ1
A square picture frame has a round circle cut out to show the picture. What is the area of the picture frame?
Will mark brainlyest!!
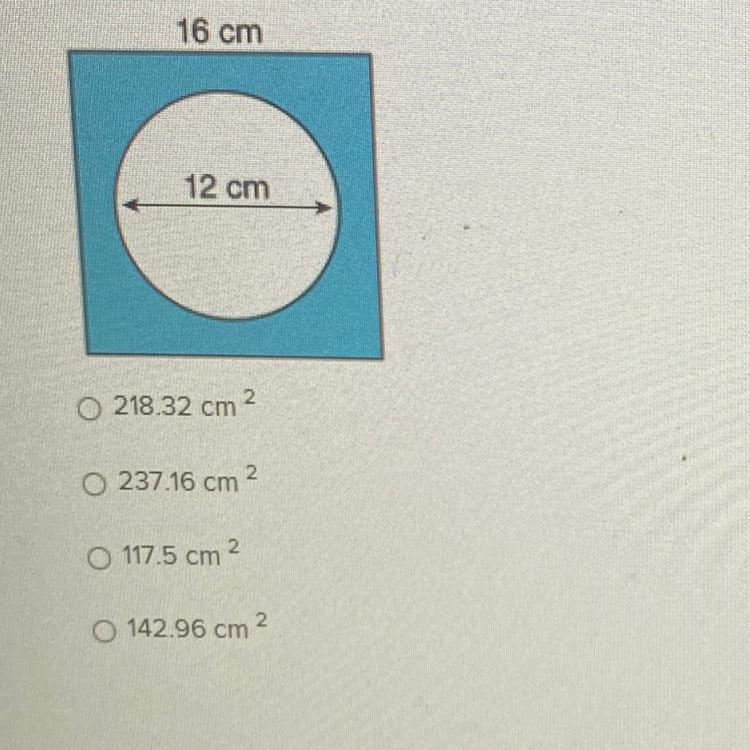
Answers
Answer:
117.5
Step-by-step explanation:
hope this helps! have a great day
what is 100x100 because im having real trouble
Answers
Answer:
10000
here you gooooooooo
Answer:
100x100=10000
Find the Fourier transform of the function f(x)=e −α∣x∣
cosβx, where a> 0 and β is a real number. Let F[f]= f
^
(ξ)= 2π
1
∫ −[infinity]
[infinity]
f(x)e −iξx
dx
Answers
The Fourier transform of the function \(\(f(x) = e^{-\alpha |x|} \cos(\beta x)\)\), where \(\(\alpha > 0\)\) and \(\(\beta\)\) is a real number, is given by: \(\[F[f] = \hat{f}(\xi) = \frac{2\pi}{\alpha^2 + \xi^2} \left(\frac{\alpha}{\alpha^2 + (\beta - \xi)^2} + \frac{\alpha}{\alpha^2 + (\beta + \xi)^2}\right)\]\)
In the Fourier transform, \(\(\hat{f}(\xi)\)\) represents the transformed function with respect to the variable \(\(\xi\)\). The Fourier transform of a function decomposes it into a sum of complex exponentials with different frequencies. The transformation involves an integral over the entire real line.
To derive the Fourier transform of \(\(f(x)\)\), we substitute the function into the integral formula for the Fourier transform and perform the necessary calculations. The resulting expression involves trigonometric and exponential functions. The transform has a resonance-like behavior, with peaks at frequencies \(\(\beta \pm \alpha\)\). The strength of the peaks is determined by the value of \(\(\alpha\)\) and the distance from \(\(\beta\)\). The Fourier transform provides a representation of the function f(x) in the frequency domain, revealing the distribution of frequencies present in the original function.
To learn more about Fourier transform refer:
https://brainly.com/question/32695891
#SPJ11
If n(Ax B) = 72 and n(A) = 24, find n(B).
Answers
Solving for Cartesian product n(B), we have n(B) = 72 / 24 = 3.
What is Cartesian product?The Cartesian product is a mathematical operation that takes two sets and produces a set of all possible ordered pairs of elements from both sets.
In other words, if A and B are two sets, their Cartesian product (written as A × B) is the set of all possible ordered pairs (a, b) where a is an element of A and b is an element of B.
For example, if A = {1, 2} and B = {3, 4}, then A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}.
By the question.
We know that n (Ax B) represents the number of elements in the set obtained by taking the Cartesian product of sets A and B.
Using the formula for the size of the Cartesian product, we have:
n (Ax B) = n(A) x n(B)
Substituting the given values, we get: 72 = 24 x n(B)
To learn more about set:
https://brainly.com/question/8053622
#SPJ1
help please anybody hmm

Answers
Answer:
94.6-18.8=75.8
75.8 is the answer
Step-by-step explanation:
Hope this helps
May i get braineist pls?
which equation represents the relationships between x and y

Answers
Answer:
y = x + 3
Hope it helps!!!!
Find each side length.
у
х
45
3
Ox= 3, y = 32
Ox=3V2, y=32
x = 3/2 y=3
x = 3, y = 6/2

Answers
The diagonals of rhombus ABCD intersect at E . Given that m(angle) BAC = 53° DE = 8 and EC = 6 find m(angle) DAC.
m(angle) DAC =

Answers
Answer:
53°
Step-by-step explanation:
You want the measure of angle DAC in rhombus ABCD with angle BAC marked as 53°.
Angle bisectorsEach diagonal of a rhombus bisects its vertex angles.
∠DAC = ∠BAC = 53°
16p + 8 = 2(8p+4) dkdaw
Answers
We prove that both side are equal.
In the given question,
The given expression is 16p + 8 = 2(8p+4).
We have to prove that both side are equal.
To solve this question we use have to follow some rule.
Some Rules are
We have to remove parentheses from each side of the equation and combine similar phrases to make it simpler.To separate the variable term on one side of the equation, use addition or subtraction.To find the variable, use division or multiplication.In this given question to solve the expression we firstly solve the bracket.
To solve this question we use Distributive Property
In this property a(b+c) = ab+ac
Solving the expression
16p + 8 = 2×8p+2×4
16p + 8 = 16p+8
Hence, we prove that both side are equal.
To learn more about Distributive Property link is here
https://brainly.com/question/5637942
#SPJ1
1. Let the distribution of X be the normal distribution N (μ, σ2) and let Y = aX + b. Prove that Y is distributed as N (aμ + b, a2σ2).
2. Let X and Y be two independent random variables with E|X| < [infinity], E|Y| < [infinity] and E|XY| < [infinity]. Prove that E[XY] = E[X]E[Y].
Answers
1 Y is distributed as N(aμ + b, a^2σ^2), as desired.
2 We have shown that under these conditions, E[XY] = E[X]E[Y].
To prove that Y is distributed as N(aμ + b, a^2σ^2), we need to show that the mean and variance of Y match those of a normal distribution with parameters aμ + b and a^2σ^2, respectively.
First, let's find the mean of Y:
E(Y) = E(aX + b) = aE(X) + b = aμ + b
Next, let's find the variance of Y:
Var(Y) = Var(aX + b) = a^2Var(X) = a^2σ^2
Therefore, Y is distributed as N(aμ + b, a^2σ^2), as desired.
We can use the definition of covariance to prove that E[XY] = E[X]E[Y]. By the properties of expected value, we know that:
E[XY] = ∫∫ xy f(x,y) dxdy
where f(x,y) is the joint probability density function of X and Y.
Then, we can use the fact that X and Y are independent to simplify the expression:
E[XY] = ∫∫ xy f(x) f(y) dxdy
= ∫ x f(x) dx ∫ y f(y) dy
= E[X]E[Y]
where f(x) and f(y) are the marginal probability density functions of X and Y, respectively.
Therefore, we have shown that under these conditions, E[XY] = E[X]E[Y].
Learn more about distributed here:
https://brainly.com/question/29664127
#SPJ11
Legolas shoots 3 arrows at once from his bow. He has 177 arrows. How many times can Legolas shoot his bow before he needs more arrows?
Answers
Answer:
59
Step-by-step explanation:
3x=177
3x represents the # of arrow he can shoot at once every time
177 represents the total # of arrow he has
Answer:
59
Step-by-step explanation:
177/3=59
What is the slope of the line?

Answers
Answer:
1/2
Step-by-step explanation:
Slope equals rise over run. To find this use two points that land evenly on the graph then count how ever many spaces up and then to the side. In this case, it goes up 1 and right 2, so put that into fraction form, 1/2, and that is your answer.
Answer:
1/2
Step-by-step explanation:
the varlance around the regression line varles with values of the predictor varlable.
Answers
In linear regression, the variance around the regression line represents the variability of the dependent variable (response variable) that is not explained by the regression model.
It measures the dispersion of the actual data points around the predicted values from the regression line.
The variance around the regression line can vary with different values of the predictor variable. This is because the relationship between the predictor variable and the response variable may not be constant across the entire range of the predictor variable. In other words, the spread or dispersion of the data points around the regression line may change as the predictor variable changes.
By examining the residuals (the differences between the observed values and the predicted values from the regression line) and calculating their variances, you can assess the variability of the data points around the regression line. This variability is an important aspect of understanding the goodness of fit of the regression model and the accuracy of the predictions.
To learn more about regression visit;
https://brainly.com/question/32505018
#SPJ11
chose the correct correspondence
Answers
The angle R corresponds to the angle E.
This comes from the fact that they are alternate interior angles.
The cost C (in dollars) for ordering and storing x units is C = 4x + 100,000 x . What order size will produce a minimum cost? (Round your answer to the nearest whole number.)
x = units
Answers
The cost C (in dollars) for ordering and storing x units is C = 4x + 100,000 x. We can calculate it in the following manner.
The minimum cost of the order size can be obtained by differentiating the given expression of the cost C (in dollars) with respect to x and equating it to 0.
So, we have C(x) = 4x + 100,000/x
Differentiating both sides with respect to x, we get: C′(x) = 4 - 100,000/x²C′(x) = 0 for minimum C(x)∴ 4 - 100,000/x² = 0
Thus, we have x² = 100,000/4= 25,000
Order size x = ± 25,000
Taking positive value for the order size, we get:x = 25000
Therefore, the order size that will produce a minimum cost is 25,000. Answer: 25,000.
To find the minimum cost, we need to minimize the function C(x) = 4x + 100,000/x. To do this, we will find the critical points by taking the derivative of the function and setting it to zero.
dC/dx = 4 - 100,000/x^2
Now, set dC/dx = 0:
4 - 100,000/x^2 = 0
Add 100,000/x^2 to both sides:
4 = 100,000/x^2
Now, multiply both sides by x^2:
4x^2 = 100,000
Divide both sides by 4:
x^2 = 25,000
Take the square root of both sides:
x = sqrt(25,000)
x ≈ 158.11
Since we need to round to the nearest whole number, the order size that will produce a minimum cost is 158 units.
Visit here to learn more about whole number brainly.com/question/29766862
#SPJ11
An isosceles triangle has an angle that measures 50° which other angles could be in that isosceles triangle
Answers
Answer:
50 and 80 or 65 and 65
Step-by-step explanation:
two angles in an isosceles are the same.
Order the numbers from least to greatest

Answers
please also explain how
(3) How do you cut a 14 inch pizza into three pieces of equal area using two parallel cuts? (Assume the cuts are placed symmetrically from the center.)
Answers
To cut a 14-inch pizza into three equal area pieces using two parallel cuts placed symmetrically from the center, each piece will have an area of 150.
As we need to cut a 14-inch pizza into three pieces of equal area using two parallel cuts, we have to follow the steps given below
:Step 1: Cut the pizza with a line that goes through the center of the pizza and marks its diameter. This cut separates the pizza into two equal halves.
Step 2: The second cut needs to be made parallel to the first cut and needs to be at a distance of approximately 1/3 the diameter of the pizza from the first cut.
Step 3: Then, the pizza will be separated into three equal area pieces as required. As we have to cut the pizza into three equal area pieces, the area of each piece will be 150 square inches.
Learn more about parallel
https://brainly.com/question/22746827
#SPJ11
Point B is on line segment AC.
Given AB=13 and BC=2, determine the length AC
Answers
Answer:
15
Step-by-step explanation:
AB+BC= AC
13+2= 15
A student completes 25 of a science project in 34 hour. At this rate, what fraction of the project can the student complete per hour?.
Answers
The student can complete 25/34 of the science project per hour based on their current rate of progress.
To determine the fraction of the project the student can complete per hour, we divide the number of completed parts by the time taken.
The student has completed 25 parts of the science project in 34 hours. To find the fraction completed per hour, we divide the number of completed parts (25) by the number of hours (34).
Therefore, the fraction of the project completed per hour is 25/34. This means that for every hour of work, the student completes approximately 25/34 of the project. This fraction represents the rate or efficiency at which the student is progressing on the project, indicating how much work is accomplished in a given unit of time.
Learn more about Fraction here: brainly.com/question/10354322
#SPJ11
The slope of the line going through the ordered pairs (12, -7) and (-9, 3) is −1021. true or false
Answers
Answer:
Use the slope formula to find the slope of a line given the coordinates of two points on the line. The slope formula is m=(y2-y1)/(x2-x1), or the change in the y values over the change in the x values.
The answer is true