If A C D H is a parallelogram, B is the midpoint of AC , and F is the midpoint of HD , write a flow proof to prove that A B F H is a parallelogram.
Answers
By utilizing the properties of parallelogram and the midpoint theorem, we can establish the parallelism of sides in quadrilateral ABFH, given that ABCD is a parallelogram with B as the midpoint of AC and F as the midpoint of HD.
To prove that ABFH is a parallelogram, we will use a flow proof with the following steps:
Given: ABCD is a parallelogram, B is the midpoint of AC, and F is the midpoint of HD.Since ABCD is a parallelogram, its opposite sides are parallel. We can write AB || CD and AD || BC.By the midpoint theorem, we know that if a line segment is divided by a point into two equal segments, then the line segment is parallel to the base. Thus, AB || CD and AC || BD.Since AB || CD and AC || BD, by the transitive property of parallel lines, we can conclude that AB || BD.Similarly, since AD || BC and AC || BD, by the transitive property of parallel lines, we can conclude that AD || BC.Now, we have AB || BD and AD || BC, which satisfy the definition of a parallelogram. Therefore, ABFH is a parallelogram.By using the properties of parallelograms and the midpoint theorem, we have shown that ABFH is a parallelogram.
Learn more about parallelogram here:
https://brainly.com/question/28831543
#SPJ11
Related Questions
A survey of 1780 american households found that 59% of the households own a computer. identify the population, the sample, and the individuals in the study.
Answers
Population: All American households.
Sample: The 1780 American households surveyed.
Individuals: The American households participating in the survey.
In the given scenario, we have a survey of 1780 American households that found 59% of the households own a computer. Let's identify the population, sample, and individuals in the study:
Population: The population refers to the entire group or larger set of individuals that we are interested in. In this case, the population would be all American households.
Sample: The sample is a subset of the population that is chosen to represent the population accurately. In this situation, the survey includes 1780 American households. Therefore, the sample is the 1780 households that were surveyed.
Individuals: The individuals in the study are the specific units or elements being surveyed or examined. In this case, the individuals are the American households that participated in the survey. Each household represents an individual within the study.
To summarize:
Population: All American households.
Sample: The 1780 American households surveyed.
Individuals: The American households participating in the survey.
Learn more about population from
https://brainly.com/question/25896797
#SPJ11
For the function
\(f(x)=3x^{2} -1\)
i)Restrict the domain to monotonic increasing and determine the inverse function over this domain
ii)State the domain and range of \(f^{-1} (x)\)
iii) Graph\(f(x)\) and \(f^{-1} (x)\) on the same set of axes
Answers
The inverse function over the domain is f⁻¹(x) = √[(x + 1)/3]
The domain and the range are x ≥ -1 and y ≥ 0
The graph of f(x) = 3x² - 1 and f⁻¹(x) = √[(x + 1)/3] is added as an attachment
Determining the inverse function over the domainFrom the question, we have the following parameters that can be used in our computation:
f(x) = 3x² - 1
So, we have
y = 3x² - 1
Swap x and y
x = 3y² - 1
Next, we have
3y² = x + 1
This gives
y² = (x + 1)/3
So, we have
y = √[(x + 1)/3]
This means that the inverse function is f⁻¹(x) = √[(x + 1)/3]
Stating the domain and rangeFor the domain, we have
x + 1 ≥ 0
So, we have
x ≥ -1
For the range, we have
y ≥ 0
The graph on the same set of axesThe graph of f(x) = 3x² - 1 and f⁻¹(x) = √[(x + 1)/3] on the same set of axes is added as an attachment
Read more about inverse function at
https://brainly.com/question/3831584
#SPJ1
![For the function [tex]f(x)=3x^{2} -1[/tex]i)Restrict the domain to monotonic increasing and determine](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/OEpdUrIhdGJuYicoYU0v9gdPqBwrbanv.png)
A cuboid with dimensions 45 cm by 16 cm by 12 cm is cut to form smaller cubes of
length 4 cm. What is the maximum number of cubes that can be obtained?
Answers
Answer:
135 is the maximum number of cubes that can be obtained

It has been found that 40% of the employees who complete a sequence of executive seminars go on to become vice presidents. Assume that 10 graduates of the program are randomly selected.Find the probability that exactly 5 become vice presidents. (Note: please give the answer as a real number accurate to3 decimal places after the decimal point.)
Answers
The probability that exactly 5 out of 10 graduates become vice presidents is 0.2007 or 0.201 (rounded to three decimal places).
We can use the binomial distribution to solve this problem.
Let X be the number of graduates who become vice presidents out of the 10 selected.
Then X follows a binomial distribution with parameters n = 10 and p = 0.4. We want to find the probability that exactly 5 become vice presidents, i.e., P(X = 5).
Using the formula for the binomial probability mass function, we have:
P(X = 5) = (10 choose 5) *\((0.4)^5 * (0.6)^5\)
P(X = 5) = (252) * (0.01024) * (0.07776)
P(X = 5) = 0.2007
Therefore,
The probability that exactly 5 out of 10 graduates become vice presidents is 0.2007 or 0.201 (rounded to three decimal places).
To know more about probability refer to this :
https://brainly.com/question/24756209
#SPJ4
let a and b be two disjoint events. under what conditions are they independent?
Answers
Disjoint events are events that cannot happen at the same time. Two events A and B are independent if the occurrence of A does not affect the probability of B happening, and vice versa. Mathematically, this can be written as P(A and B) = P(A)P(B).
In the case of disjoint events, P(A and B) = 0 because they cannot occur at the same time. Therefore, the condition for A and B to be independent is that either P(A) = 0 or P(B) = 0, since any non-zero probability for either event would make the product P(A)P(B) also non-zero.
Two disjoint events are independent if and only if at least one of them has zero probability.
To learn more about probability : brainly.com/question/32004014
#SPJ11
Consider the function below. Find f(5).
f(x) = -2x + 7
Answers
Answer:
f(5) = -3
Step-by-step explanation:
f(x) = -2x + 7
f(5) = -2(5) + 7
f(5) = -10 + 7
f(5) = -3
The value of the function at x = 5 will be equal to f(5) = -3
What is a function?The expression that established the relationship between the dependent variable and independent variable is referred to as a function. In the function as the value of the independent variable varies the value of the dependent variable also varies.
Given that the function is f(x) = -2x + 7. The value of the function at x=5 will be calculated as,
f(x) = -2x + 7
f(5) = -2(5) + 7
f(5) = -10 + 7
f(5) = -3
Therefore, the value of the function at x = 5 will be equal to f(5) = -3.
To know more about a function follow
https://brainly.com/question/24748644
#SPJ5
Find an orthonormal basis for the orthogonal complement of the row space of the matrix A= ⎣
⎡
1
0
2
2
3
0
0
1
0
0
0
1
⎦
⎤
(Hit: What well known ypace is the orthogonal complement of the column space of a matrix?)
Answers
Each of these vectors is already normalized, so they form an orthonormal basis for R^4, which is the orthogonal complement of the row space of matrix A.
To find an orthonormal basis for the orthogonal complement of the row space of matrix A, we need to find a basis for the null space of the transpose of matrix A, which is the orthogonal complement of the column space.
Let's begin by finding the transpose of matrix A:
A = ⎣⎡ 1 0 2 2 3 0 0 1 0 0 0 1 ⎦⎤
A^T = ⎣⎡ 1 2 0 0 0 3 1 0 2 0 0 1 ⎦⎤
Next, we will perform row reduction on the transpose of A to find the basis for the null space.
RREF(A^T) = ⎣⎡ 1 0 0 00 1 0 0 0 0 1 0 0 0 0 1 ⎦⎤
From the row-reduced echelon form of A^T, we can observe that the columns of A^T form the standard basis vectors of R^4, indicating that the null space of A^T is the zero vector space.
Therefore, the orthogonal complement of the row space of matrix A is the entire space R^4. To find an orthonormal basis for R^4, we can use the standard basis vectors:
{e1, e2, e3, e4} = {⎣⎡ 1 0 0 0 ⎦⎤ , ⎣⎡ 0 1 0 0 ⎦⎤, ⎣⎡ 0 01 0 ⎦⎤, ⎣⎡0 0 0 1 ⎦⎤ }
Each of these vectors is already normalized, so they form an orthonormal basis for R^4, which is the orthogonal complement of the row space of matrix A.
Learn more about vector from
https://brainly.com/question/28028700
#SPJ11
Geometry
Please help !
Would the answer be z is 64?
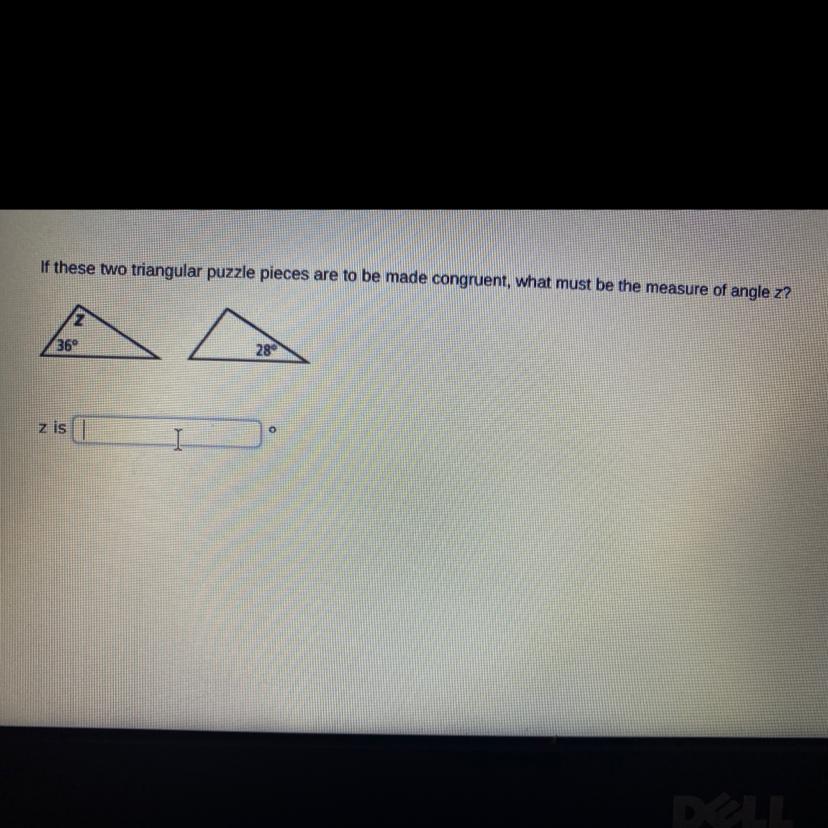
Answers
Evaluate. 68.14 + 0.0007
Answers
Answer:
68.1407 us the answer
Step-by-step explanation:
Just add
5. In A LMN, LM = 12, LN = 10. and angle L = 52° What is the length, to the nearest tenth of a unit, of MN?
7.4 units
15.6 units
9.8 units
14.4 units
Answers
The length of MN, to the nearest tenth of a unit is equal to: C. 14.4 units.
What is the law of cosine?In order to determine the missing side length of a geometric figure with the adjacent and hypotenuse side lengths given, you should apply the law of cosine:
C² = A² + B² - 2(A)(B)cosθ
Where:
A, B, and C is the length of side of a given triangle.
By substituting the given side lengths and angle into the law of cosine formula, we have the following;
MN² = LM² + LN² - 2(LM)(LN)cosθ
MN² = 12² + 10² - 2(12)(10)cos(52)
MN² = 144 + 100 - 147.76
MN = √96.24
MN = 9.8 units.
Read more on cosine here: brainly.com/question/11000638
#SPJ1
find the inflection point of the function. (hint: g ' ' ( 0 ) g′′(0) does not exist.) g ( x ) = 9 x | x |
Answers
The inflection point of g(x) = 9|x| is x = 0.
First, let's find the first derivative of g(x):
g'(x) = 9 |x| + 9x * d/dx(|x|)
g'(x) = 9 |x| + 9x * sign(x)
where sign(x) is the sign function, which equals -1 for x < 0, 0 for x = 0, and 1 for x > 0.
Now, let's find the second derivative of g(x):
g''(x) = 9 * d/dx(|x|) + 9 * sign(x) + 9x * d/dx(sign(x))
g''(x) = 0 + 9 * sign(x) + 9x * d/dx(sign(x))
The derivative of the sign function is not defined at x = 0, but we can use the definition of the derivative to find the left and right limits of g''(x) as x approaches 0:
g''(0-) = lim x→0- [g''(x)]
g''(0-) = lim x→0- [9 * (-1) + 9x * (-∞)]
g''(0-) = -∞
g''(0+) = lim x→0+ [g''(x)]
g''(0+) = lim x→0+ [9 * (1) + 9x * (∞)]
g''(0+) = ∞
Since the left and right limits of g''(x) as x approaches 0 are not equal, g''(0) does not exist, and g(x) does not have an inflection point. Instead, the function changes concavity at x = 0, which is a vertical point of inflection.
To know more about inflexion point, here
https://brainly.com/question/28639394
#SPJ4
I need help with math

Answers
The measure of arc AD is 126°
What is circle geometry?A circle is a special kind of ellipse in which the eccentricity is zero and the two foci are coincident.
There is a theorem in circle geometry that states that angles in thesame segment are equal.
Therefore;
11x -3 = 8x +15
collecting like terms
11x -8x = 15 +3
3x = 18
divide both sides by 3
x = 18/3
x = 6
therefore angle C
= 8x +15 = 8(6)+15
= 48+15
= 63
Therefore arc AD
= 2 × angle C
arc AD = 63 × 2 = 126°
Therefore the measure of arc AD is 126°
learn more about circle geometry from
https://brainly.com/question/24375372
#SPJ1
A cigarette manufacturer wishes to test the claim that the variance of nicotine content of its cigarettes is less than 0.0644. Nicotine content is measured in milligrams and is assumed normally distributed. A sample of 20 cigarettes has a mean of 1.00 milligram with a standard deviation 0.17. At 0.05 level of significance, is there enough evidence to reject the manufacturer's claim? 1.State the test hypotheses. H0 : Vs. H1 : 2. what is its sampling distribution? (normal or t-student or Chi square or F distribution) 3. Find the test statistic 4. What is the critical v 4. What is your decision regarding H0 ? Reject H0 or don't reject H0 ?
Answers
1. The test hypotheses are:
H0: The variance of nicotine content of the cigarettes is greater than or equal to 0.0644.
H1: The variance of nicotine content of the cigarettes is less than 0.0644.
2. The sampling distribution for testing the variance is the chi-square distribution.
3. To find the test statistic, we will use the chi-square test statistic formula:
Test Statistic = ((n-1) * s^2) / σ^2
Where:
n = sample size = 20
s^2 = sample variance = (0.17)^2 = 0.0289
σ^2 = hypothesized variance = 0.0644
Plugging in the values:
Test Statistic = ((20-1) * 0.0289) / 0.0644
= (19 * 0.0289) / 0.0644
≈ 8.5098
4. To determine the critical value, we need to find the chi-square value corresponding to a significance level of 0.05 and degrees of freedom equal to n-1 = 19.
Using a chi-square distribution table or a statistical software, we find the critical value to be approximately 30.144.
5. Since the test statistic (8.5098) is less than the critical value (30.144), we do not have enough evidence to reject the null hypothesis (H0). Therefore, we fail to reject the manufacturer's claim that the variance of nicotine content of its cigarettes is greater than or equal to 0.0644.
Learn more about test hypotheses from :
https://brainly.com/question/4232174
#SPJ11
how do you multiply
Answers
Answer:
example 7 x 3 means you add 7 3 times
Step-by-step explanation:
find the area of the triangle

Answers
verify the identity by converting the left side into sines and cosines. (simplify at each step.) 8 cot(x) sec(x) = 8 csc(x) − 8 sin(x)
Answers
8 cot(x) sec(x) can be simplified to 8 csc(x) - 8 sin(x) by converting the left side into sines and cosines.
How can the expression 8 cot(x) sec(x) be simplified using trigonometric identities?
To verify the identity by converting the left side into sines and cosines, we'll simplify each step.
Starting with the left side of the equation:
8 cot(x) sec(x)
First, let's express cot(x) and sec(x) in terms of sines and cosines:
cot(x) = cos(x) / sin(x)
sec(x) = 1 / cos(x)
Substituting these values back into the equation:
8 (cos(x) / sin(x)) (1 / cos(x))
Next, we can cancel out the common terms of cos(x):
8 (1 / sin(x))
Finally, we can rewrite 1 / sin(x) as csc(x):
8 csc(x)
Therefore, the left side of the equation simplifies to 8 csc(x).
The right side of the equation is already in the desired form:
8 csc(x) - 8 sin(x)
Thus, we have successfully shown that the left side of the equation, after converting to sines and cosines, simplifies to the right side of the equation. The identity is verified.
Learn more about sines and cosines,
brainly.com/question/31129851
#SPJ11
The type of competitive structure that exists in the case where there are almost no substitutes for a product is a(n) Group of answer choices pure competition. monopoly. noncompetition. monopolistic competition. oligopoly.
Answers
The type of competitive structure that exists when there are almost no substitutes for a product is a monopoly.
A monopoly occurs when there is a single seller or producer in the market with exclusive control over the supply of a particular product or service. In this scenario, there are no close substitutes available to consumers, meaning that the monopolistic firm has a significant degree of market power and can dictate prices and output levels without facing significant competition.
The absence of substitutes is a key characteristic of a monopoly market structure. Due to the lack of alternatives, consumers have limited choices and are compelled to purchase the product from the monopolistic firm, often at higher prices. This lack of competition allows the monopolistic firm to maintain a dominant position and enjoy high profit margins.
Learn more about prices here:
https://brainly.com/question/19091385
#SPJ11
I was gone for 2 days in school and have no idea how to do this, anyone mind helping.

Answers
They are perpendicular lines.
What do you notice about the equations for the two lines?
They are opposite of each other.
Solve x(x-3)=0 please find this quick
Answers
\(x \times (x - 3) = 0 \\this \: means \: that \: \\ either \: x = 0 \: or \: (x - 3) = 0\)
\(so \: x = 0\)
\(x - 3 = 0\)
\(x = 3\)
so,
\(x = 0 \: or \: 3\)
Triangle XYZ has vertices X(8, −2.3), Y(6.5, 5), and Z(6, 3). When translated, X′ has coordinates (3.8, −0.3). Enter a rule to describe this transformation. Then find the coordinates of Y′ and Z′. Drag and drop each number into the correct box to complete the statements. The rule is (x, y) arrowright parenleftzex − , y + parenrightze. The coordinates are Y′parenleftze, parenrightze and Z′parenleftze, parenrightze.
Answers
Answer:
The coordinates of \(Y'(x,y)\) and \(Z'(x,y)\) are \(Y'(x,y) = (2.3, 7)\) and \(Z'(x,y) = (1.8, 5)\), respectively.
Step-by-step explanation:
A translation is a geometrical operation consisting in moving a point a given distance. We proceed to describe the operation:
\(X(x,y) +U(x,y) = X'(x,y)\) (Eq. 1)
Where:
\(X(x, y)\) - Initial point on the cartesian plane, dimensionless.
\(X'(x, y)\) - Translated point on the cartesian plane, dimensionless.
\(U(x, y)\) - Translation component, dimensionless.
Vectorially speaking, we find that translation component is:
\(U(x, y) = X'(x,y) -X(x,y)\)
If we know that \(X(x,y) = (8, -2.3)\) and \(X'(x,y) = (3.8, -0.3)\), the translation component is:
\(U(x,y) = (3.8,-0.3)-(8,-2.3)\)
\(U(x,y) = (3.8-8, -0.3+2.3)\)
\(U(x,y) = (-4.2, 2)\)
Now we determine the coordinates of \(Y'(x,y)\) and \(Z'(x,y)\):
(\(Y(x,y) = (6.5, 5)\), \(Z(x,y) = (6,3)\))
\(Y'(x,y) = Y(x,y) + U(x,y)\) (Eq. 2)
\(Y'(x,y)=(6.5, 5) + (-4.2, 2)\)
\(Y'(x,y) = (2.3, 7)\)
\(Z'(x,y) = Z(x,y) + U(x,y)\) (Eq. 3)
\(Z'(x,y) = (6,3)+(-4.2,2)\)
\(Z'(x,y) = (1.8, 5)\)
The coordinates of \(Y'(x,y)\) and \(Z'(x,y)\) are \(Y'(x,y) = (2.3, 7)\) and \(Z'(x,y) = (1.8, 5)\), respectively.
pls help i beg you!
A plumber charges a flat fee of $79 to visit a home and examine a clogged drain. The plumber charges an additional $24 per hour spent fixing the drain. The total cost, C (in dollars), for fixing a drain that takes H hours is given by the following.
c=79+24h
Answer the following questions.
(a)
What is the total cost for fixing a drain that takes 7 hours?
$?
(b)
If the plumber charged a total of $343, how many hours did he spend fixing the drain?
?hours
Answers
Answer:
for "A" the answer is 247$
For "B" the answer 11 hours
Step-by-step explanation:
What is the equation of a line that contains the point (2,-5) and is parallel to
the line: y = 3x - 4?
O A. y = -1/3x-13/3
O B. y = 3x -4
O C. y = 3x - 11
O D. y = -1/3x - 4
Answers
Answer:
C. y=3x-11
Step-by-step explanation:
y=3x-4
m=3
y=mx+b
-5=3(2)+b
b= -5-6= -11
y=3x-11
Math problem help plz
(don't send links will report u)
ASAp

Answers
For what value of a does 9 = (startfraction 1 over 27 endfraction) superscript a + 3?.
Answers
When the start fraction is 1 and the end fraction is 27, the value is a=-11/3.
What is meant by a fraction?A fraction is a part of a whole or, more broadly, any number of equal parts. In ordinary English, a fraction describes the number of components of a specific size and consists of a numerator displayed above a line (or before a slash like 12) and a non-zero denominator displayed below (or after) that line.
In addition to common fractions, numerators and denominators are used in rare fractions such as compound fractions, complex fractions, and mixed numerals.
Positive common fractions have natural integers as their numerator and denominator.
Here we need to find the value of n for which 9=(1/27)ᵃ⁺³
Now, we have to rewrite with a base of 3 we get,
3²=3⁻³.3ᵃ⁺³
2=-3(a+3)
2=-3a-9
=2+9=-3a
11=-3a
a=-11/3
Therefore, the values is a=-11/3
To know more about fraction, visit:
https://brainly.com/question/10354322
#SPJ4
if x+3y upon 5x+4y= 1/3 find the ratio of x:y ANSWER FASTTT
Answers
Answer:
x : y = 5 : 2
Step-by-step explanation:
Given
\(\frac{x+3y}{5x+4y}\) = \(\frac{1}{3}\) ( cross- multiply )
5x + 4y = 3(x + 3y)
5x + 4y = 3x + 9y ( subtract 3x from both sides )
2x + 4y = 9y ( subtract 4y from both sides )
2x = 5y ( divide both sides by 2 )
x = \(\frac{5}{2}\) y ( divide both sides by y )
\(\frac{x}{y}\) = \(\frac{5}{2}\) , that is
x : y = 5 : 2
Answer:
x/y = 5/2
Step-by-step explanation:
hello :
(x+3y) /( 5x+4y)= 1/3 means : 5x+4y = 3(x+3y)
5x+4y = 3x+9y
5x-3x = 9y - 4y
2x = 5y
now divid by y : 2x/y = 5y/y
2x/y = 5 so : x/y = 5/2
The captain of the cheerleading team, Alicia, counted that they washed 58 cars. Determine if this is a reasonable number of cars that could've been washed.
Answers
Answer:
yes but no
Step-by-step explanation:
um well that is a lot by not if there is a bunch of people doing it.
What is the value of 3 minus (negative 2)?
A number line going from negative 5 to positive 5.
–5
–1
1
5
Answers
Answer:
5
Step-by-step explanation:
I hope this helps if this is wrong please correct me! :)
The value of 3 minus (negative 2) is 5.
Given that we need to simplify 3 minus (negative 2), which is at a number line going from negative 5 to positive 5.
To find the value of 3 minus (negative 2), we can simplify the expression.
When we subtract a negative number, it is the same as adding its positive counterpart.
Mathematically,
3 - (-2)
We know, when minus sign multiplied by minus sign it becomes positive.
So, we can rewrite the expression as 3 + 2.
Adding 3 and 2 gives us 5.
Therefore, the value of 3 minus (negative 2) is 5.
Learn more about Arithmetic operations click;
https://brainly.com/question/30553381
#SPJ6
The denominator of a rational number is greater than the numerator by 10. If the numerator is increased by 1 and the denominator is decreased by 1, then expression for new denominator is——
x+1
x +10
x - 10
x + 9
Answers
The denominator of a rational number is greater than the numerator by 10. If the numerator is increased by 1 and the denominator is decreased by 1, then expression for new denominator is x + 9.
Find value of P and Q
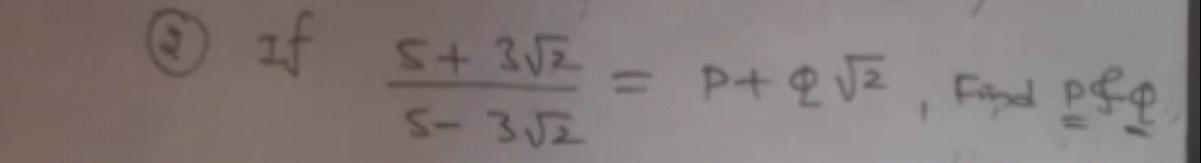
Answers
Answer:
\( P= 6 \frac{1}{7}\\\\
Q = 4 \frac{2}{7}\)
Step-by-step Explanation
\( \frac{5 + 3 \sqrt{2} }{5 - 3 \sqrt{2} } = P+Q\sqrt 2 \\ \\ \frac{(5 + 3 \sqrt{2}) }{(5 - 3 \sqrt{2}) } \times \frac{(5 + 3 \sqrt{2}) }{(5 + 3 \sqrt{2} )} = P+Q\sqrt 2 \\ \\ \frac{ {(5 + 3 \sqrt{2} )}^{2} }{ {(5)}^{2} - (3 \sqrt{2})^{2} } = P+Q\sqrt 2 \\ \\ \frac{ {5}^{2} + {(3 \sqrt{2} )^{2} + 2.5.3 \sqrt{2} } }{25 - 9 \times 2} = P+Q\sqrt 2 \\ \\\frac{ 25 + 18 + 30 \sqrt{2} }{25 - 18} = P+Q\sqrt 2 \\ \\\frac{ 43 + 30 \sqrt{2} }{7} = P+Q\sqrt 2 \\ \\ \frac{43}{7} + \frac{30 }{7} \sqrt{2} = P+Q\sqrt 2 \\ \\ equating \: like \: terms \: on \: both \: sides \\ \\ P = \frac{43}{7} \\ \\ \huge \red { \boxed{ P= 6 \frac{1}{7}}} \\ \\ Q = \frac{30}{7} \\ \\ \huge \orange { \boxed{ Q = 4 \frac{2}{7} }}\)
Please i need help When is the product of the square root of a prime number and a nonzero rational number a rational number?
Answers
Answer:
The product of the square root of a prime number and a nonzero rational number is a irrational number.
Step-by-step explanation:
Given that,
When is the product of the square root of a prime number and a nonzero rational number a irrational number.
We know that,
Prime number :
Prime number is that number whose has a two factor. first factor is one and second is themselves.
The square root of a prime number is irrational number.
Rational number :
Rational number is that number which is in fraction form.
For example : \(\dfrac{p}{q}\)
Here, p and q are integers
We need to proof the product of the square root of a prime number and a nonzero rational number is a rational number
Using given data
Suppose, the square root = √5
Rational number = \(\dfrac{2}{3}\)
We need to calculate the product of the square root of a prime number and a rational number
Using formula of product
\(R=P\timesQ\)
Where, P = square root of a prime number
Q= rational number
Put the value into the formula
\(R=\sqrt{5}\times\dfrac{2}{3}\)
\(R=\dfrac{2\sqrt{5}}{3}\)
Hence, The product of the square root of a prime number and a nonzero rational number is a irrational number.