Carol is solving the inequality 3
have?
There are infinitely many solutions.
There are only two solutions.
There is only one solution.
There are no solutions.
Answers
Answer:
There are infinitely many solutions
Step-by-step explanation:
Firstly, I need to change f to x as the system won’t accept the word f
Let’s take a look at the question;
3 is less than x
The domain of our answer lies in the the range of values where we have numbers that are greater than 3
This means we can rewrite our inequality as x is greater than 3
Now, simply because we have an infinite amount of numbers which are greater than 3 of which x can take any of the values, we can conclude that the number of values we have for x are infinite and does not end
This makes us have infinitely many solutions for the value of x
Related Questions
Which was Ismail known for?

Answers
Answer:
The third one
Step-by-step explanation:
The price of an item has risen to $301 today. Yesterday it was $140 Find the percentage increase.
Answers
Answer: 115%
Step-by-step explanation: ur welcome
Answer:
53.2%
Step-by-step explanation:
301x53.2%= 160.132 = 160.13
301-160.13=140.87
About 53.2%
Simplify.
6.5-7.48 -3.4 + 3.8
Answers
Answer:
-0.58
Step-by-step explanation:
6.5 - 7.48 = -0.98-0.98 - 3.4 = -4.38-4.38 + 3.8 = -0.58I hope this helps!
Find the percent change from the first value to the second. Round to the nearest percent.
80; 60.
Answers
Answer:
25% decrease
Step-by-step explanation:
=(60−80)|80|×100
=−2080×100
=−0.25×100
=−25%change
=25%decrease
Answer:
25% decrease
Step-by-step explanation:
Evaluate the expression when b=3 b to the power of 2 + 14
Answers
Answer:
25
Step-by-step explanation:
b=3
b^2+14=?
3^2+14=?
9+14=?
9+14=25
(0)
A production line operates for two eight-hour shifts each day. During this time, the production line is expected to produce 3,000 boxes. What is the takt time in minutes?
Group of answer choices
.25
.3
3
.6
Answers
The expected number of boxes to be produced is given as 3,000 boxes. So, the correct answer is 0.3, indicating that the takt time in minutes is 0.3 minutes.
The production line operates for two eight-hour shifts each day, which means there are 16 hours of production time available. Since there are 60 minutes in an hour, the total available time in minutes would be 16 hours multiplied by 60 minutes, which equals 960 minutes.
The expected number of boxes to be produced is given as 3,000 boxes.
To calculate the takt time in minutes, we divide the total available time (960 minutes) by the expected number of boxes (3,000 boxes):
\(Takt time = Total available time / Expected number of boxes\)
\(Takt time = 960 / 3,000\)
By performing the calculation, we find that the takt time is approximately 0.32 minutes, which is equivalent to 0.3 minutes rounded to one decimal place.
Learn more about minutes here:
https://brainly.com/question/31148642
#SPJ11
Can someone help me please and thankyou
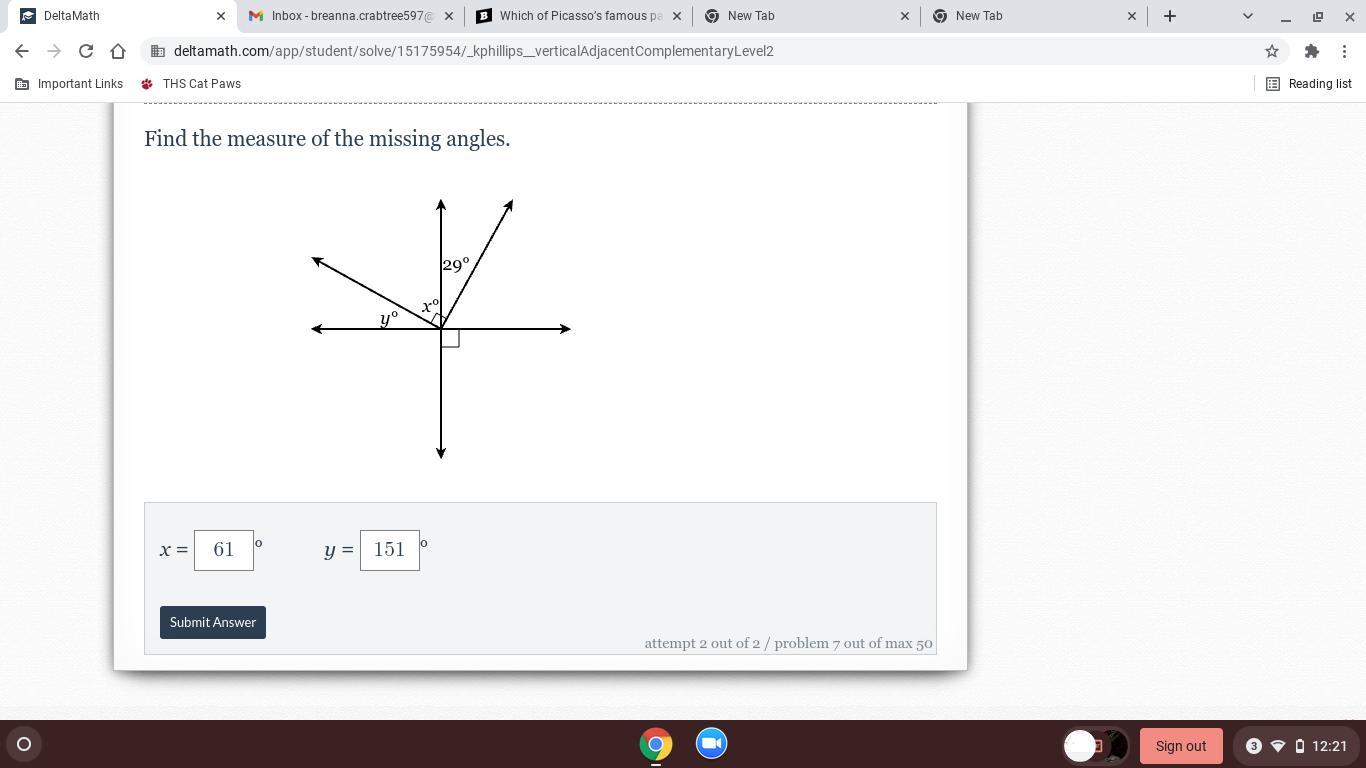
Answers
= 61°
y°= 90°- 61°
= 29°
find y and x right?
1.2 = 2.4 – 0.6x
Please help meeeeee
Answers
Answer:
x=2
Step-by-step explanation:
Explanation:
Subtract 2.4 on both sides
-1.2 = -0.6x
divide by -0.6 on both sides and it leaves you with
x=2
for an anova, the within-treatments variance provides a measure of the variability inside each treatment condition.true or false
Answers
In ANOVA (Analysis of Variance), the total variability in the data is partitioned into two components: True. The within-treatments variance in an ANOVA provides a measure of the variability inside each treatment condition.
In ANOVA (Analysis of Variance), the total variability in the data is partitioned into two components: the between-treatments variability and the within-treatments variability. The between-treatments variability represents the differences among the treatment conditions, while the within-treatments variability measures the variability within each treatment condition.
The within-treatments variance, also known as the error variance or residual variance, quantifies the variation that cannot be attributed to the differences among treatment conditions. It captures the random variability within each treatment group, accounting for the individual differences and random errors present within the groups.
By analyzing the within-treatments variance, we can assess how much variation exists within each treatment condition and evaluate the consistency or homogeneity of the data within each group. It helps determine the extent to which the treatment conditions explain the observed differences and whether any remaining variation is due to random fluctuations or other factors.
Hence, the statement that the within-treatments variance provides a measure of the variability inside each treatment condition is true in the context of ANOVA.
Learn more about ANOVA here:
https://brainly.com/question/31192222
#SPJ11
For what value of is the function defined below continuous on (−[infinity],[infinity])? f(x)= { x^2 - c^2, x < 6
{ cx + 45, x ≥ 6
Answers
The function \(f(x) = x^2 - c^2\) for x < 6 and f(x) = cx + 45 for x ≥ 6 is continuous on (-∞, ∞) for all values of c except for c = 0. Consider the definition of continuity.
A function is continuous at a point if the limit of the function as x approaches that point exists and is equal to the value of the function at that point.
For x < 6, the function \(f(x) = x^2 - c^2\) is a polynomial function and is continuous for all values of c since polynomials are continuous everywhere.
For x ≥ 6, the function f(x) = cx + 45 is a linear function. Linear functions are also continuous everywhere, regardless of the value of c.
However, at x = 6, we have a point of discontinuity if c = 0. When c = 0, the function becomes f(x) = 45 for x ≥ 6. In this case, the function has a jump discontinuity at x = 6 since the limit as x approaches 6 from the left is not equal to the value of the function at x = 6.
In conclusion, the function \(f(x) = x^2 - c^2\) for x < 6 and f(x) = cx + 45 for x ≥ 6 is continuous on (-∞, ∞) for all values of c except when c = 0.
Learn more about polynomial here: https://brainly.com/question/25117687
#SPJ11
The complete question is:
For What Value Of The Constant C Is The Function F Defined Below Continuous on (−[infinity],[infinity])?
f(x)= { x² - c², x < 6
{ cx + 45, x ≥ 6
please help it’s for geometry
assume lines p and q intersect to form adjacent angles 1 and 2.
if m<1 = (4x-3) and m<2 = (3x+8). find the value of x such that <1 is supplementary to <2

Answers
Answer:
x=25
Step-by-step explanation:
they are supplementary and adjacent, thus you do 4x-3+3x+8=180, simplify and get 7x+5=180, subtract 5 from 180 which is 175, then ending up with 7x=175 and 175/7 is 25.
Answer:
Step-by-step explanation:
why are we able to solve the wason task with examples (whether one is 21 and drinking alcohol) rather than letters and numbers? group of answer choices
Answers
The Wason selection test measures a person's ability to recognize information that challenges a certain hypothesis, in this case, a type of conditional hypothesis. if P, then Q.
Given,
Wason's Card;
A popular tool for studying problem resolution that was developed in 1966 by English psychologist Peter C(athcart) Wason (1924–2003). The uppermost faces of the four cards, which are arranged on a table, display the letters and numerals E, K, 4, and 7.
What is demonstrated by the Wason selection task?
As a result, the Wason selection test gauges how well people can spot evidence that refutes a certain hypothesis, in this case, a conditional hypothesis of the type. P, then Q if.
For example;-
The majority of people have no trouble choosing the proper cards ("16" and "drinking beer") if the rule is "If you are drinking alcohol, then you must be over 18" and the cards contain an age and beverage on one side, respectively.
Learn more about Wason's card here;
https://brainly.com/question/14274430
#SPJ4
i eill drop a picture
Answers
Parallel lines have the same slope, that is
\(\begin{gathered} m_1=m_2_{} \\ \text{ Where} \\ m_1\text{ is the slope of line 1 and} \\ m_2\text{ is the slope of line 2} \end{gathered}\)The slope of line 1 is 1/3 because its equation is written in slope-intercept form, that is
\(\begin{gathered} y=mx+b \\ \text{ Where m is the slope and} \\ \text{b is the y-intercept} \\ y=\frac{1}{3}x-1\Rightarrow\text{ Line 1} \\ m_1=\frac{1}{3}\Rightarrow\text{ Slope of the line 1} \end{gathered}\)Now, since the slopes are parallel then you already have the slope of line 2:
\(\begin{gathered} m_1=m_2 \\ \frac{1}{3}=m_2 \end{gathered}\)Then, you can use the point-slope equation to find the equation for line 2:
\(\begin{gathered} y-y_1=m(x-x_1)\Rightarrow\text{ Point-slope equation} \\ \text{ Where m is the slope and} \\ (x_1,y_1)\text{ is a point through which the line passes} \end{gathered}\)So, you have
\(\begin{gathered} m_2=\frac{1}{3} \\ (x_1,y_1)=(6,10) \\ y-y_1=m(x-x_1) \\ y-10=\frac{1}{3}(x-6) \end{gathered}\)Finally, to obtain the equation of the line in its slope-intercept form, solve for y:
\(\begin{gathered} y-10=\frac{1}{3}(x-6) \\ \text{ Apply the distributive property to the right side of the equation} \\ y-10=\frac{1}{3}x-\frac{1}{3}\cdot6 \\ y-10=\frac{1}{3}x-2 \\ \text{ Add 10 from both sides of the equation} \\ y-10+10=\frac{1}{3}x-2+10 \\ y=\frac{1}{3}x+8 \end{gathered}\)Therefore, the equation in slope-intercept form of the line that passes through (6,10) and is parallel to the given equation is
\(y=\frac{1}{3}x+8\)and the correct answer is option A.
please help me I only have 2 minutes left winner gets brainliest when did Qin Shi Huang become ruler
Answers
Answer: 221 B.C
Step-by-step explanation:
Answer:
221 B.C.
Step-by-step explanation:
The state of Qin, based in the Sichuan plains, eventually won out in 221 B.C. under the leadership of the ruthless King Zheng. The victorious monarch gave himself the title Qin Shi Huangdi (259–210 B.C.), First Qin Emperor.Jun 3, 2019
true or false: a) every unitary operator u : x ! x is normal. b) a matrix is unitary if and only if it is invertible.
Answers
True, Every normal unitary operator u: x! x exists.
False, An if only if it is invertible, a matrix qualifies as unitary.
What is the matrix?
A group of numbers built up in a rectangular array with rows and columns. The elements, or entries, of the matrix, are the integers. In addition to numerous mathematical disciplines, matrices find extensive use in the fields of engineering, physics, economics, and statistics.
Here, we have
a. Every unitary operator U:X→X is normal as an operator A is unitary if A*A = AA* = I and an operator is normal if A*A = AA*.
Hence, every unitary operator u: x → x is normal.
b. A unitary matrix is always invertible but an invertible matrix need not be unitary. An invertible matrix A is unitary if A⁻¹ = A*
Hence, it is not true.
To learn more about the matrix from the given link
https://brainly.com/question/12567347
#SPJ4
Plis reply fast and get brainless

Answers
Answer:
number 1 - 2 is bigger ----- Number 2 - 1 is bigger ------ Number three - 5 is bigger
Step-by-step explanation:
The mean monthly mortgage paid by all home owners in a town is $2365 with a standard deviation of $340. a. Using Chebyshev's theorem, find the minimum percentage of all home owners in this town who pay a monthly mortgage of $1685 to $3045. b. Using Chebyshev's theorem, find the interval that contains the monthly mortgage payments of at least 84% of all home owners in this town.
Answers
According to Chebyshev's theorem, we can determine the minimum percentage of home owners in the town who pay a monthly mortgage between $1685 and $3045, as well as the interval that contains the monthly mortgage payments of at least 84% of all home owners.
a. Chebyshev's theorem states that for any data set, regardless of its shape, at least (1 - 1/k^2) percent of the data falls within k standard deviations of the mean, where k is any positive constant greater than 1. In this case, we want to find the percentage of home owners whose monthly mortgage falls within $1685 and $3045, which is within 1 standard deviation of the mean in either direction. The standard deviation given is $340, so the range for 1 standard deviation would be $2365 ± $340. Therefore, the minimum percentage of home owners in this town who pay a monthly mortgage of $1685 to $3045 is at least (1 - 1/1^2) = 0% according to Chebyshev's theorem.
b. To find the interval that contains the monthly mortgage payments of at least 84% of all home owners, we need to determine the range within which 84% of the data falls. Chebyshev's theorem tells us that at least (1 - 1/k^2) percent of the data lies within k standard deviations of the mean. We want to find the range within which at least 84% of the data falls, so we need to solve the inequality (1 - 1/k^2) ≥ 0.84.
Rearranging the inequality, we get 1/k^2 ≤ 0.16, which implies k^2 ≥ 6.25. Taking the square root of both sides, we find k ≥ 2.5. Thus, 84% of the data lies within 2.5 standard deviations of the mean. Multiplying the standard deviation of $340 by 2.5 gives us a range of $850. Therefore, the interval that contains the monthly mortgage payments of at least 84% of all home owners in this town is $2365 ± $850, or $1515 to $3215.
Learn more about standard deviations here:
https://brainly.com/question/29115611
#SPJ11
The amunt of money that college students spend on rent each month is usually between $300 and $600. However, there are a few students who spend $1,300. What measure of spread would be most appropriate to measure the amount of money that college student spend on rent per month? Explain in detail why or why not one of the below measures would be used.
A. Median
B. Range
C. Standard Deviation
D. Inquartile Range
Answers
The range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
To measure the amount of money college students spend on rent per month, the most appropriate measure of spread would be the range. The range is the simplest measure of spread and is calculated by subtracting the lowest value from the highest value in a data set. In this case, the range would be $1,300 - $300 = $1,000.
The median would not be the best choice in this scenario because it only represents the middle value in a data set. It does not take into account extreme values like the $1,300 rent expense.
Standard deviation would not be the most appropriate measure of spread in this case because it calculates the average deviation of each data point from the mean. However, it may not accurately represent the spread when extreme values like the $1,300 rent expense are present.
The interquartile range (IQR) would not be the best choice either because it measures the spread of the middle 50% of the data set. It does not consider extreme values and would not accurately represent the range of rent expenses in this scenario.
In summary, the range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
Know more about Standard deviation here,
https://brainly.com/question/29115611
#SPJ11
A book has 6 chapters in it, each with the same number of pages.
•The book also has an introduction that is 8 pages long.
•The whole book is 194 pages long.
Write an equation using x below.
Answers
An equation using x as the number of pages in the book that has 6 chapters with the same number of pages and an introduction with 8 pages is 6x + 8 = 194.
What is an equation?An equation is a mathematical statement that defines that two or more mathematical or algebraic expressions are equal or equivalent.
Equations use the equal symbol (=) while mathematical expressions just combine variables with numbers, constants, and values using mathematical operands.
The number of chapters in the book = 6
The number of pages of the introduction = 8 pages
The total number of pages of the whole book = 194
Let the number of pages in each chapter = x
Equation:6x + 8 = 194
6x = 186 (194 - 8)
x = 31
Thus, we can evaluate the equation to show that x is 31.
Learn more about equations at https://brainly.com/question/22688504.
#SPJ1
Question Completion:Write an equation using x to show the number of pages in each chapter of the book.
Can someone please help me

Answers
Because when you’re finding the slope of a line you rise/run. Defined the B of a slope intercept equation you find where the line is intersecting the Y axis
Answer:
Y=.833x-2
Step-by-step explanation:
correct y intercept and rise over run gives you the slope.
Which of the following best describes the angles shown?
Captionless Image
Vertical angles
Horizontal angles
Linear Pairs
Planar Pairs
None of the above

Answers
help please! and hurry.

Answers
Answer:
Place it one mark before 2.
What two numbers multiply to get 18 but add to get -12
Answers
Answer:
-6+3\(\sqrt{2}\) and -6-3\(\sqrt{2}\)
Step-by-step explanation:
xy = 18
x+y = -12
y = -12-x
substitution method:
x(-12-x) = 18
-12x - x² - 18 = 0
-x² - 12x - 18 = 0
-(x² + 12x + 18) = 0
used quadratic formula:
(-12±√144 - 4(18)) ÷ 2
(-12 ± \(\sqrt{72}\)) ÷ 2
(-12 ± 6\(\sqrt{2}\)) ÷ 2
= -6 ± 3\(\sqrt{2}\)
Which statement best explains why this expression is equal to 9.4? A)Any expression multiplied by 0 equals 0. B)Any number divided by its opposite equals 0. C)The fraction is equal to −9.4. Any number added to its opposite results in the number itself. D)The expression does not have a value of 9.4.

Answers
Answer: A.
Step-by-step explanation:
yeet
Answer:
A.
Step-by-step explanation:
Because if you multiply out the top of the fraction to simplify it, it will equal zero. And zero divided by any number is equal to zero because no number fits into zero. So A. would be the best answer since you are multiplying an expression by zero on the top, and you can't get any number other then zero for the answer of the fraction. And 0 + 9.4 = 9.4.
The sum of two numbers is 36. Four times the smaller is one less than the larger. Find the numbers
Answers
12 and 3 because 3 divided by 12=4 and 12x3=36
a baseball player has a batting average of 0.265. what is the probability that he has exactly 4 hits in his next 7 at bats?
Answers
The probability that he has exactly 4 hits in his next 7 at-bats is 0.0018.
It is given that,
P(hits) = 0.265= p
For his next 7 bats, n= 7
Let X be the number of hits in the next 7 bats
Given that there can only be two outcomes—the probability of success and the probability of failure—this probability typically follows a binomial distribution.
X~ Binomial ( 7, 0.265)
substituting values
P( X=6) = ⁷C₆ (0.265)^6 (1-0.265) = 0.0018
Here ⁷C₆ means 7 combinations 6.
thus, the probability that he has exactly 4 hits in his next 7 at-bats is 0.0018.
Know more about binomial distribution here: https://brainly.com/question/17154501
#SPJ4
ingths for the modified and unmodified mortars, respectively. Assume that the bond strength distributions are both normal. (a) Assuming that σ 1
=1.6 and σ 2
=1.3, test H 0
:μ 1
−μ 2
=0 versus H a
:μ 1
−μ 2
>0 at level 0.01 . Calculate the test statistic and determine the P-value. (Round your test statistic to two decimal places and your P-value to four State the conclusion in the problem context. Reject H 0
. The data suggests that the difference in average tension bond strengths exceeds 0. Fail to reject H 0
. The data does not suggest that the difference in average tension bond strengths exceeds from 0 . Reject H 0
. The data does not suggest that the difference in average tension bond strengths exceeds 0. Fail to reject H 0
. The data suggests that the difference in average tension bond strengths exceeds 0. (b) Compute the probability of a type II error for the test of part (a) when μ 1
−μ 2
=1. (Round your answer to four decimal places.) number.) n= (d) How would the analysis and conclusion of part (a) change if σ 1
and σ 2
were unknown but s 1
=1.6 and s 2
=1.3 ? follow. Since n=32 is not a large sample, it still be appropriate to use the large sample test. The analysis and conclusions would stay the same. Since n=32 is a large sample, it would be more appropriate to use the t procedure. The appropriate conclusion would follow.
Answers
(a) The test statistic and P-value:The given information is provided as follows:σ1 = 1.6 and σ2 = 1.3The hypothesis test is defined as follows: H0: μ1 − μ2 = 0Ha: μ1 − μ2 > 0The significance level is α = 0.01.The two-tailed test for the difference between two means is given by:
(x1 ¯-x2 ¯)-(μ1-μ2)/sqrt[s1^2/n1+s2^2/n2]=t where s1^2 and s2^2 are variances of the sample 1 and sample 2 respectively. From the question, the sample size n1 = 27, and sample size n2 = 32.
Substitute the given values of n1, n2, σ1, and σ2 into the formula above to calculate the value of the test statistic:
t = [(92.7 − 87.4) − (0)] / √[(1.6^2 / 27) + (1.3^2 / 32)] = 2.28
The P-value is P(t > 2.28) = 0.013.
Hence the test statistic is 2.28 and the P-value is 0.013.The appropriate conclusion would be:Reject H0. The data suggests that the difference in average tension bond strengths exceeds 0. The P-value of 0.013 is less than the significance level α = 0.01.
(b) The probability of a type II error for the test of part (a) when μ1 − μ2 = 1:The type II error occurs when we fail to reject the null hypothesis when it is actually false. It is denoted by β.To calculate β, we need to determine the non-rejection region when the alternative hypothesis is true.
The non-rejection region is given by:t ≤ tc where tc is the critical value of t at the 0.01 level of significance and (n1 + n2 – 2) degrees of freedom.From the t-tables, tc = 2.439.
To calculate β, we need to find the probability that t ≤ tc when μ1 − μ2 = 1. Let d = μ1 − μ2 = 1.
Then,β = P(t ≤ tc; μ1 − μ2 = d) = P(t ≤ 2.439; μ1 − μ2 = 1).
Now, we have t = [(x1 ¯-x2 ¯) - (μ1-μ2)]/ sqrt [s1^2/n1 + s2^2/n2] = (x1 ¯-x2 ¯-d)/sqrt [s1^2/n1 + s2^2/n2]
Hence,P(t ≤ 2.439; μ1 − μ2 = 1) = P[(x1 ¯-x2 ¯)/ sqrt [s1^2/n1 + s2^2/n2] ≤ (2.439 − 1)/sqrt [(1.6^2/27) + (1.3^2/32)]] = P(z ≤ 0.846) = 0.7998,
where z is the standard normal distribution variable.
Therefore, the probability of a type II error for the test of part (a) when μ1 − μ2 = 1 is 0.7998.
(d) How would the analysis and conclusion of part (a) change if σ1 and σ2 were unknown but s1 = 1.6 and s2 = 1.3?The analysis would be done using the t-distribution, since σ1 and σ2 are not known and the sample size is small (n1 = 27 and n2 = 32). The hypothesis test and the test statistic are the same as in part
(a).However, the standard errors should be replaced with the estimated standard errors using the sample standard deviations s1 and s2 as follows:SE = sqrt [(s1^2/n1) + (s2^2/n2)] = sqrt [(1.6^2/27) + (1.3^2/32)] = 0.462.The t-value is calculated as:
t = [(x1 ¯-x2 ¯)-(μ1-μ2)]/SE = [(92.7 − 87.4) − (0)] / 0.462 = 11.48.The P-value is P(t > 11.48) < 0.0001. Therefore, the conclusion is the same as in part (a): Reject H0.
The data suggests that the difference in average tension bond strengths exceeds 0.
To know more about test statistic visit:
https://brainly.com/question/31746962
#SPJ11
i need help!!!!!!!!!!

Answers
Answer:
a is 4+x
b is x/3
c is 2x+9
d is 2x-12
Step-by-step explanation:
(2) five cards are dealt from a standard 52-card deck. (a) how many such hands have only black cards? (b) how many such hands have a full house of aces and fives (3 aces and 2 fives)?g
Answers
The total number of hands with a full house of aces and fives is 36 * 10 = 360.
(a) To find the number of hands with only black cards:
Step 1: There are 26 black cards in a standard 52-card deck (13 spades and 13 clubs).
Step 2: We need to choose 5 black cards from the 26 available.
Step 3: Use the combination formula: C(n, k) = n! / (k!(n-k)!) where n is the total number of items and k is the number of items we want to choose.
Step 4: Calculate C(26, 5) = 26! / (5!(26-5)!) = 26! / (5!21!) = 65,780.
Answer (a): There are 65,780 hands with only black cards.
(b) To find the number of hands with a full house of aces and fives:
Step 1: There are 4 aces and 4 fives in a standard 52-card deck.
Step 2: Choose 3 aces from the 4 available (C(4, 3)).
Step 3: Choose 2 fives from the 4 available (C(4, 2)).
Step 4: Multiply the combinations from steps 2 and 3: C(4, 3) * C(4, 2).
Step 5: Calculate C(4, 3) = 4! / (3!(4-3)!) = 4.
Step 6: Calculate C(4, 2) = 4! / (2!(4-2)!) = 6.
Step 7: Multiply the results from steps 5 and 6: 4 * 6 = 24.
Answer (b): There are 24 hands with a full house of aces and fives.
to learn more about number click here:
brainly.com/question/30752681
#SPJ11
A store ships cans by weight.
A small box can hold 3 to 5 pounds. A medium box can hold 5 to 8 pounds.
The weights of the cans are given below.
Drag cans into each box to show what the box could contain.

Answers
Answer: In the small box you can put 9 small cans and 1 big can
0.25 x 9 = 2.25
2.25+2.7=4.95
In the big box, you can put 2 big cans and 10 small can
2.7x2= 5.4
0.25x10 =2.5
5.4+2.5=7.9
let me know if that's right