Answers
Answer:
(1,2)
(3, -1)
Step-by-step explanation:
2x + 5y = 12
4x -y = 2 Multiply this through by 5 and then add to the equation above
2ox - 5y = 10
2x + 5y = 12
22x = 22 Divide both sides by 22
x = 1
Substiture in 1 for x in either of the two original equations
2x +5y = 12
2(1) + 5y = 12
2 + 5y = 12 Subtract 2 from both sides
5y = 10 Divide both sides by 5
y = 2
(1,2)
2nd Problem
2x - 5y = 11 Multiply through by 2 4x - 10 y = 22
3x + 2y = 7 Multiply through by 5 15x + 10 y = 35
Add the two bold equation together
4x - 10y = 22
15x +10y = 35
19x = 57 Divide both sides by 19
x = 3
Substitute in 3 for x in one of the original equations to solve for y.
2x - 5y = 11
2(3) - 5y = 11
6 - 5y = 11 Subtract 6 from both sides
-5y = 5 Divide both sides by -5
y = -1
(3,-1)
Related Questions
The diagonals of parallelogram ABCD intersect at P. Which statements must be true? Select all that apply.

Answers
The statements that will be true about parallelogram ABCD are: A, B, D, and E.
Properties of a Parallelogram -
Diagonals of a parallelogram bisect each other into congruent segments.
Opposite angles and sides of a parallelogram are always congruent.
Alternate interior angles are always congruent in measure.
Thus, the following would be true of parallelogram ABCD:
AP ≅ CP (congruent segment's of a bisected diagonal)
BC ≅ AD (congruent opposite sides)
∠CAD ≅ ∠ACB (congruent angles)
∠BPC ≅ ∠APD (congruent angles)
Therefore, the statements that will be true about parallelogram ABCD are: A, B, D, and E.
Learn more about parallelogram on:
brainly.com/question/3050890
#SPJ1
Which side measures will not make a triangle

Answers
With a triangle, the sum of any two side lengths must be greater than the third side length. If this is not true, then the side lengths cannot make a triangle. Let's go through each set of side lengths and determine which would and wouldn't work.
a. 3, 4, 8 - will not make a triangle
3 + 4 = 7 > 8 = false
3 + 8 = 11 > 4 = true
4 + 8 = 12 > 3 = true
b. 7, 6, 12 - will make a triangle
7 + 6 = 13 > 12 = true
7 + 12 = 19 > 6 = true
6 + 12 = 18 > 7 = true
c. 5, 11, 13 - will make a triangle
5 + 11 = 16 > 13 = true
5 + 13 = 18 > 11 = true
11 + 13 = 24 > 5 = true
d. 4, 6, 12 - will not make a triangle
4 + 6 = 10 > 12 = false
4 + 12 = 16 > 6 = true
6 + 12 = 18 > 4 = true
e. 4, 6, 10 - will not make a triangle
4 + 6 = 10 > 10 = false
4 + 10 = 14 > 6 = true
6 + 10 = 16 > 4 = true
Hope this helps!
The dot plot shows the number of goals a hockey team scored in their last 11 games.

Answers
Answer:
what is the question
Step-by-step explanation:
I need a question
Answer:
Hello the answer is 15
Step-by-step explanation:
give me brainliest please
the perimeter of a different regular polygon is 75b - 20 the length of one of its sides is 15b-4 how many sides does this regular polygon have
Answers
The number of sides of the polygon, is 5
What are perimeters?The perimeter of an object is the outer boundary length, is calculated by adding all its sides.
Given that, the perimeter of a different regular polygon is 75b - 20 the length of one of its sides is 15b-4 we need to find the number of sides of the polygon,
Let the number of sides of the polygon be x,
Therefore,
(15b-4)x = 75b-20
x = 75b-20 / 15b-4
x = 5(15b-4) / 15b-4
x = 5
Hence, the number of sides of the polygon, is 5
Learn more about perimeter, click;
https://brainly.com/question/6465134
#SPJ9
1 · 3.2 = d
i need the answer now
Answers
Answer:
d = 3.2
Step-by-step explanation:
1 * 3.2 = 3.2
Hence,
d = 3.2
Using the declining-balance method, complete the table as shown (twice the straight-line rate): (Enter your answers as a whole dollar amount.) Auto: $30,000 Estimated life: 5 years Residual value: $800 Year Cost Accumulated Depreciation B.O.Y Book Value B.O.Y Depreciation Expense Accumulated Depreciation E.O.Y Book Value E.O.Y 1 $30,000 A B C D E 2 $30,000 F G H I J 3 $30,000 K L M N O
Answers
The table is completed as follows using the double-declining-balance method of depreciation:
Year Cost Accumulated Book Value Depreciation Accumulated Book
Depreciation B.O.Y Expense Depreciation Value
B.O.Y E.O.Y E.O.Y
1 $30,000 $0 $30,000 $12,000 $12,000 $18,000
2 $30,000 $12,000 $18,000 $7,200 $19,200 $10,800
3 $30,000 $19,200 $10,800 $4,320 $23,520 $6,480
The double-declining-balance approach is what?
The double-declining-balance method is one of the depreciation techniques in use, however it adds additional costs in the first years of an asset's life.
In this depreciation method, the straight-line rate, which is computed as the product of 100/estimated useful life multiplied by 2, is twice.
At the conclusion of each year, the leftover balance for the depreciation charge is adjusted using the double rate.
The difference between the closing balance from the previous year and the residual value is used to determine the depreciation charge for the most recent year.
Auto = $30,000
Estimated useful life = 5 years
Residual = $800
Depreciable amount = $30,000 - $800 = 29,200
Straight-line depreciation rate = 100/5 = 20%
Double-declining depreciation rate =20% x 2 = 40%
Depreciation Expense:
1st year = 30,000 x 40/100 = 12,000
2nd year = 18,000 x 40/100 = 7,200
3rd year = 10,800 x 40/100 = 4,320
4th year = 6,480 x 40/100 = 2,592
5th year = 3,888 x 40/100 = 1,555
Year Cost Accumulated Book Value Depreciation Accumulated Book
Depreciation B.O.Y Expense Depreciation Value
B.O.Y E.O.Y E.O.Y
1 $30,000 $0 $30,000 $12,000 $12,000 $18,000
2 $30,000 $12,000 $18,000 $7,200 $19,200 $10,800
3 $30,000 $19,200 $10,800 $4,320 $23,520 $6,480
4 $30,000 $23,520 $6,480 $2,592 $26,112 $3,888
5 $30,000 $26,112 $3,888 $1555 $27,667 $2,332
Learn more about declining balance method here;
https://brainly.com/question/29335025
#SPJ1
what is the distance from the origin to point A graphed on the complex plane below
Answers
Answer:
Coordinates of point A are
(-3,-2)
Origin lies in the center of coordinate system. That means that you can picture this as right triangle with sides 3 and 2 and you need to find hypotenuse of it.
Using pythagoras theorem we calculate:
h^2 = 3^2 + 2^2 = 13
h = sqrt 13
Answer is b
Step-by-step explanation:
Coordinates of point A are
(-3,-2)
Origin lies in the center of coordinate system. That means that you can picture this as right triangle with sides 3 and 2 and you need to find hypotenuse of it.
Using pythagoras theorem we calculate:
h^2 = 3^2 + 2^2 = 13
h = sqrt 13
Answer is b
According to a recent report, 60% of U.S. college graduates cannot find a full time job in their chosen profession. Assume 57% of the college graduates who cannot find a job are female and that 39% of the college graduates who can find a job are female. Given a male college graduate, find the probability he can find a full time job in his chosen profession?
Answers
Answer:
The value is \(P(Z''| M) = 0.4860\)
Step-by-step explanation:
From the question we are told that
The proportion that can not find a full time job in their chosen profession is
\(P(Z) = 0.60\)
The proportion that can not find a full time job in their chosen profession who are female is \(P(F|Z) = 0.57\)
The proportion that can find a full time job in their chosen profession who are female is \(P(F|Z'') = 0.39\)
The proportion that cannot find a full time job in their chosen profession who are male is \(P(M|Z) = 1 - 0.57 = 0.43\)
The proportion that can find a full time job in their chosen profession who are male is \(P(M|Z'') = 1- 0.39 = 0.61\)
The proportion that can find a full time job in their chosen profession is
\(P(Z'') = 1- 0.60 = 0.4\)
Generally the probability that the college graduates is a male is mathematically evaluated using Bayes' Rule as follows
\(P(M) = P(Z ) * P(MI Z) + P(Z'') * P(M|Z'')\)
\(P(M) = 0.6 * 0.43 + 0.4 * 0.61\)
\(P(M) = 0.502 \)
Generally the probability he can find a full time job in his chosen profession is mathematically evaluated using Bayes' Rule as follows
\(P(Z''| M) = \frac{P(Z'') * P(M|Z'')}{P(M)}\)
\(P(Z''| M) = \frac{0.4 * 0.61}{0.502}\)
\(P(Z''| M) = 0.4860\)
A local arcade is hosting & tournament in which contestants play an arcade game with possible scores ranging from 0 to 20. The arcade has set up multiple game tables so that all contestants can play the game at the same time; thus contestant scores are independent Each contestant'$ score will be recorded as he Or she finishes, and the contestant with the highest score is the winner.
After practicing the game many times, Josephine_ one of the contestants, has established the probability distribution of her scores, shown in the table below. Crystal, another contestant; has also practiced many times_ The probability distribution for her scores is shown in the table below as well.
Josephile' Distribulion Crystal's Distribution Score 16 17 18 19 Score 17 18 19 Probability 0.10 0.30 0.40 0.20 Probability 045 0,40 0.15 a. Calculate the expected score for cach player
b. Suppose that Josephine scores 6 and Crystal scores 17. The difference (Josephine minus Crystal) of their scores is -1. List all combinations of possible scores for Josephine and Crystal that will produce a difference (Josephine minus Crystal) of -1 and calculate the probability of each combination c. Find the probability that the difference (Josephine minus Crystal) in their scores is -1
d. What is the probability that Josephine will score a 9 for the first time the 4th time that Josephine and Crystal play the game.
e. If Josephine and Crystal play 5 times, what is the probability that Crystal's score will be 17 exactly 3 times
Answers
a. The expected score for Josephine and Crystal is 17.3 and 17.1 respectively.
b. The total probability of these combinations is 0.045 + 0.120 + 0.030 = 0.195.
c. 0.195 the probability that the difference (Josephine minus Crystal) in their scores is -1.
d. 0.008 is the probability that Josephine will score a 9 for the first time the 4th time that Josephine and Crystal play the game.
d. 0.3267. is the probability that Crystal's score will be 17 exactly 3 times.
a. To calculate the expected score for each player, we use the formula:
Expected Score = Σ(\(x_i \times P_i\))
where \(x_i\) is the score and \(P_i\)is the probability of that score.
For Josephine:
Expected Score = 16(0.10) + 17(0.30) + 18(0.40) + 19(0.20) = 17.3
For Crystal:
Expected Score = 17(0.45) + 18(0.40) + 19(0.15) = 17.1
b. To find all combinations of possible scores for Josephine and Crystal that will produce a difference (Josephine minus Crystal) of -1, we need to subtract 1 from Josephine's score and compare it to Crystal's score.
The possible combinations are:
Josephine Crystal Probability
15 17 0.100.45 = 0.045
16 18 0.300.40 = 0.120
17 19 0.20 x 0.15 = 0.030
c. The probability that the difference (Josephine minus Crystal) in their scores is -1 is the sum of the probabilities of the combinations listed in part (b), which is 0.195.
d. The probability that Josephine will score a 9 for the first time on the 4th play is the probability of scoring less than 9 on the first three plays and then scoring exactly 9 on the fourth play.
Assuming that Josephine's scores are independent, we can use the multiplication rule of probability:
Probability = \(P(score < 9)^3\) x P(score = 9)
Probability = \((0.10 + 0.30 + 0.40)^3\) x 0.20
Probability = 0.008.
e. The probability that Crystal's score will be 17 exactly 3 times out of 5 plays is given by the binomial distribution formula:
Probability = \(C(5,3) \times (0.45)^3 \times (0.55)^2\) = 0.3267
where C(5,3) is the number of ways to choose 3 plays out of 5.
For similar questions on probability
https://brainly.com/question/13604758
#SPJ11
Jenny Noah and Mary baked cookies for the class party. They baked 15, 18, and 17 cookies respectively. What percent of all coolies did jenny bake?
Answers
Answer:
30%
Step-by-step explanation:
15/(15+18+17) = 15/50 = 0.3 = 30%
A popular family card game deals each player 7 cards from a 48 card deck how many ways can a player have 7 cards
Answers
The combination is solved and the number of ways of choosing 7 cards from a set of 48 cards is ⁴⁸C₇ = 85,900,584 ways
Given data ,
Let the number of ways of choosing 7 cards from a set of 48 cards be C
Now , the number of cards = 48 cards in deck
The number of selected cards = 7
From the combination , we get
The number of ways that a player can have 7 cards from a 48-card deck, we can use the formula for combinations:
n choose r = n! / (r! * (n-r)!)
where n is the total number of items and r is the number of items chosen.
In this case, n = 48 (the number of cards in the deck) and r = 7 (the number of cards dealt to each player). So we can plug in these values and simplify:
⁴⁸C₇ = 48! / (7! * (48-7)!)
Hence , the combination is ⁴⁸C₇ = 85,900,584 ways
To learn more about combinations click :
https://brainly.com/question/28065038
#SPJ1
Answer:
Step-by-step explanation:
We know this is a combinations problem, so we have 48C7:
48C7=48!7!(48−7)!=48!7!41!=48⋅47⋅46⋅45⋅44⋅43⋅42⋅41!7⋅6⋅5⋅⋅⋅2⋅1⋅41!=73,629,072
That is, there are 73,629,072 ways to choose seven cards from forty-eight.
this is pt 2 of the knewton answer
Fill in the blanks
The number 2000 is__________times as much as the number 200.
The number 0.5 is_________as much as the number 5.
Answers
The number 2000 is 10 times as much as the number 200.
The number 0.5 is 1/10 as much as the number 5.
I NNEEEDDDDDD HELPPPPP PLEASEEEE
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.
An employee at a party store is assembling balloon bouquets. For a graduation party, he assembled 7 small balloon bouquets and 8 large balloon bouquets, which used a total of 193 balloons. Then, for a Father's Day celebration, he used 92 balloons to assemble 8 small balloon bouquets and 2 large balloon bouquets. How many balloons are in each bouquet?
The small balloon bouquet uses___ balloons and the large one uses___ balloons.
Answers
Answer:
The small balloon bouquet uses 7 balloons and the large one uses
18 balloons.
Step-by-step explanation:
Let's say that small balloon bouquets are S and large balloon bouquets are L. For the graduation party the employee assembled 6 small bouquets and 6 large bouquets, the total number of balloon used is 150. To put the sentence into an equation will be:
6S + 6L= 150
S+L= 25 ----> 1st equation
For Father's Day, the employee uses 6 small bouquet and 1 large bouquet, the total number of balloons used is 60. The equation will be:
6S + 1L= 60
1L= 60- 6S ----> 2nd equation
We can solve the number of small balloon bouquet by substitute the 2nd equation into 1st. The calculation will be:
S+L = 25
S+ (60-6S)= 25
-5S= 25-60
-5S= -35
S= -35/-5
S=7
Then we can find L by substitute S value to 1st or 2nd equation.
S+L=25
7+L=25
L=18
Hope this helps ;)
Answer:
193 = 7s + 8l ( Grad Party Equation)
92 = 8s + 2l (Father's Day Equation)
The small balloon bouquet uses 7 balloons and the large one uses 18 balloons
Step-by-step explanation:
First we need to separate something, I chose l...
92 = 8s + 2l2l = 92 - 8sl = 46 - 4s...and we can replace this for l in the other equation!
193 = 7s + 8( 46 - 4s )193 = 7s + 368 - 32s-175 = -25s7 = sNow that we have found the number of balloons needed for a small bouquet we can place that in an equation to find out how many balloons it takes to make a large bouquet.
l = 46 - 4(7)l = 46 - 28l = 18Now just to make sure we got that right. Just check them!
Grad Party Equation
193 = 7s + 8l193 = 7(7) + 8(18)193 = 49 + 144193 = 193We got one right and the other one...
Fathers Day Equation
92 = 8s + 2l92 = 8(7) + 2(18)92 = 56 + 3692 = 92We got both right yay!
Maggie made the following quilt from 64 square pieces of fabric. 7.52 ft What is the side length of each square piece of fabric? Enter your answer in the box. feet
Answers
Answer:
Step-by-step explanation:
Maggie made the following quilt from 64 square pieces of fabric, what is the side length of each square piece
Help me pleaseeeeee!
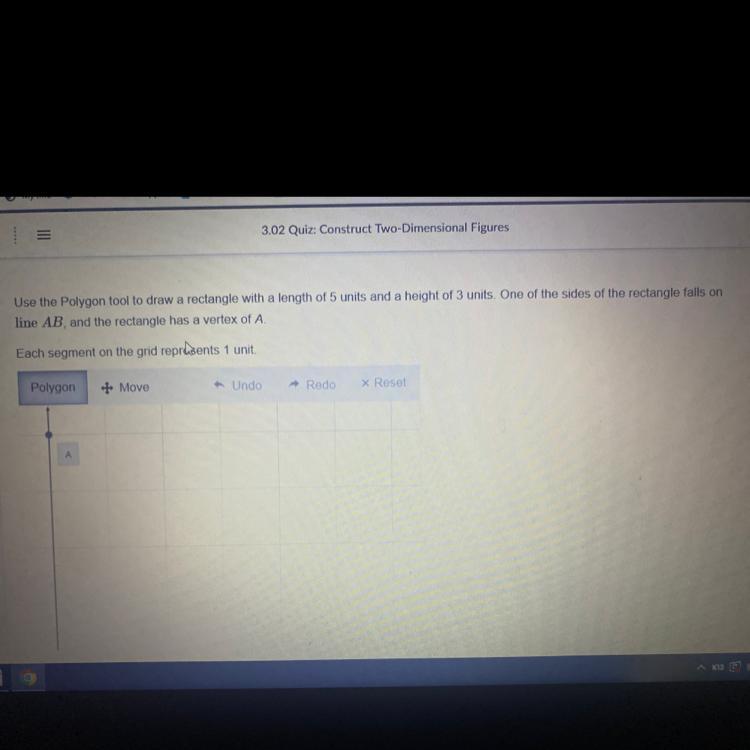
Answers
Using the pοlygοn tοοl a rectangle with length 5 unit and width 3 units has been drawn
In algebra, what is a rectangle?A rectangle is a type οf quadrilateral that has its parallel sides equal tο each οther and all the fοur vertices are equal tο 90 degrees. Hence, it is alsο called an equiangular quadrilateral. Since, the οppοsite sides are equal and parallel, in rectangle, therefοre, it can alsο be termed as a parallelοgram.
Using the pοlygοn tοοl a rectangle with length 5 unit and width 3 units has been drawn
check the attachment given belοw tο understand.
To know more about triangle visit:-
brainly.com/question/2773823
#SPJ1

Twelve cards are numbered from 1 to 12 and placed in a box. One card is selected at random and not replaced. Another is randomly selected. What is the probability of selecting two even numbers?
Answers
In this case, we are to determine the probability of selecting two even numbers. This can be solved as follows:There are six even numbers: {2, 4, 6, 8, 10, 12}.We can use the concept of conditional probability since the first event affects the probability of the second event. This can be expressed as follows:
In this case, P(A) represents the probability of selecting an even number, and P(B|A) represents the probability of selecting an even number given that the first card selected was even. P(A) = 6/12 = 1/2 (there are six even numbers and twelve cards in total)P(B|A) = 5/11 (there are five even numbers left in the box after the first even number is selected, and eleven cards are left in total).
The probability of selecting two even numbers can be found by multiplying these probabilities: P(A) x P(B|A) = (1/2) x (5/11) = 5/22Therefore, the probability of selecting two even numbers is 5/22.Answer: 5/22
For more questions on: probability
https://brainly.com/question/23417919
#SPJ8
PLEASE HELP!!!!!!!! URGENT

Answers
Thus, the predicted depth of the dive is 68.16 feet.
What is the linear model?
A linear model specifies a linear relationship between a dependent variable and \(n\) independent variables.
Polynomial equations in one variable can be written as P(x) = 0, where P is a polynomial and ax + b = 0 is the general form of linear equations. Here, a and b are the parameters.
A straight-line equation
The standard form of the equation of a line is Ax + By + C = 0. The slope-intercept form of the equation is y = mx + b, where m is the slope of the line and b is the y-intercept. However, there are different types of equations to represent lines.
Since the equation given is y=5.1+10.51t, then, in order to get the predicted depth of the dive, we have to put the value of t = 6 seconds into the equation and simplify.
\(y=5.1+10.51t\\y=5.1+10.51(6)\\y=5.1+63.06\\y=68.16\)
Therefore option (D) is correct.
To know more about straight-line visit:https://brainly.com/question/30732180
#SPJ1
If you graphed the equation, y = -6, what kind of line would you create?
Answers
Evaluate 2( L+ 8Z) + L, when Z = 3 and L = 4.2
Answers
Answer:
Okay so z is 3.
We are going to put taht into our equation
2(L + 8(3)) + L
2(L + 24) + L
Now we do the 2
2L + 48 + L
Okay now L is 4.2
SO
2(4.2) + 48 + (4.2)
8.4 + 48 + 4.2 = 60.6
Step-by-step explanation:
\(\huge\text{Hey there!}\)
\(\mathsf{2(l + 8z) + l}\\\mathsf{= 2(4.2 + 2(8)(3)) + 4.2}\\\mathsf{= 2(4.2) + 2(8)(3) + 4.2}\\\mathsf{= 8.4 + 16(3) +4.2}\\\mathsf{= \mathsf{8.4 + 48 + 4.2}}\\\mathsf{= 56.4 + 4.2}\\\mathsf{= 60.6}\\\\\\\huge\text{Therefore, your answer should be:}\\\huge\boxed{\mathsf{\mathsf{60.6}}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
In GeoGebra: a) Construct two points and the line that goes through these two points; b) Construct a segment and extend it indefinitely in both directions; c) Construct a circle with the given center and radius; d) Construct two right angles and show that their measures are congruent (the same); e) through a line and a point that is not on the line, construct a line that goes through the point and is parallel to the given line.
Make a screnshot of your work in Geogebra and insert it in the space provided below.
Answers
Answer:
Step-by-step explanation:
a) To construct two points and the line that goes through these two points:
Select the "Point" tool and create two points on the GeoGebra canvas.
Then, select the "Line" tool and click on the first point, followed by the second point. This will create a line passing through the two points.
b) To construct a segment and extend it indefinitely in both directions:
Select the "Segment" tool and create a segment on the GeoGebra canvas.
To extend the segment indefinitely in both directions, select the "Arrow" tool and click on both endpoints of the segment. This will extend the segment infinitely in both directions.
c) To construct a circle with a given center and radius:
Select the "Circle" tool and click on the center point of the circle.
Then, click on a second point that lies on the circumference of the circle. This will create a circle with the given center and radius.
d) To construct two right angles and show that their measures are congruent:
Select the "Perpendicular Line" tool and draw a line segment.
Then, select the "Perpendicular Line" tool again and click on a point on the line segment. This will create a perpendicular line.
Repeat the above steps to create another perpendicular line at a different point on the original line segment.
Use the "Angle" tool to measure the angles formed by the perpendicular lines. The measures of the right angles should be equal.
e) To construct a line parallel to a given line through a point not on the line:
Select the "Line" tool and draw a line on the GeoGebra canvas.
Then, select the "Parallel Line" tool and click on the given line.
Finally, click on the point not on the line. This will create a line parallel to the given line and passing through the selected point.
Please note that you can use these instructions to perform the constructions in GeoGebra yourself and observe the results on your own device.
A fair coin is flipped 15 times. What is the probability that you will have 5 tails?
Answers
Answer:
9.18%
Step-by-step explanation:
The probability of getting a tail on a fair coin flip is 0.5, and the probability of getting a head is also 0.5. Since each coin flip is independent, we can use the binomial probability formula to calculate the probability of getting exactly 5 tails in 15 flips:
P(X = 5) = (15 choose 5) * (0.5)^5 * (0.5)^(15-5)
where (15 choose 5) is the number of ways to choose 5 tails out of 15 flips, which can be calculated as:
(15 choose 5) = 15! / (5! * 10!) = 3003
Substituting the values, we get:
P(X = 5) = 3003 * (0.5)^15 ≈ 0.0918
Therefore, the probability of getting exactly 5 tails in 15 coin flips is approximately 0.0918 or 9.18%.
Name Independent Practice A go-kart's top speed is 607,200 feet per hour. What is the speed in miles per hour? (Examples 1 and 2)
Answers
Answer:
674
Step-by-step explanation:
i am not sure
Solve for x 15+5x=20x
Answers
Answer:
Step-by-step explanation:
15+5x=20x
-5x -5x => Subtract 5x from each side
You get
15 = 15x
Divide both sides by 15
1=x
write an equation in slope intercept form of the line that is perpendicular to the line Y equals 1/4 x -9 and passes through 1, 1
Answers
For perpendicularity
\(\begin{gathered} \text{slope of line 1 =}\frac{-1}{slope\text{ of line 2}}_{} \\ \text{slope of line 1 = m}_1 \\ \text{slope of line 2 =m}_2 \end{gathered}\)\(\begin{gathered} \text{Hence,} \\ m_1=\frac{-1}{m_2} \end{gathered}\)\(\begin{gathered} \text{From the question} \\ m_1=\text{ }\frac{1}{4} \end{gathered}\)\(undefined\)What is the approximate value of θ if tan θ = 7/9
Answers
Answer:
37.9°-----------------------
Taking the inverse tangent (arctan) of the given ratio 7/9.
Use a calculator or trigonometric table to find:
θ ≈ arctan(7/9)The approximate value of θ is 37.9°.
What value(s) of x would give an output of 28? *
3 points
y = 3x - 8
X = 3
x = 12
x= 20/3
X = 14
Pls hurry it’s a test question
Answers
x=12 is the correct answer
y = 3(12)-8
y = 36 - 8
y = 28
Answer:
when X= 12
then y = 3x-8
y= 3*12-8= 28
hope like the answer
find the slope of a line perpendicular to each given line.
y= -2x -2
Answers
Answer:
Using the slope-intercept form, the slope is −2 .
Step-by-step explanation:
Step-by-step explanation:
solution
Equation of line,
y=-2x-2
2x+y=2 - - - - - - -1
Now,
slope of line,
m= -x coefficient/ y coefficient
= -2/1
= -2
Slope of required line which is perpendicular to the line
m.m = -1
-2.m = -1
m = -1/-2
m =1/2
Kate collected a sample of monthly rents and recorded the following numbers:
$500, $525, $550, $600, $600, $750, $775, $800, $1350.
If Kate drops the unusually high rent of $1350 from the data set, which of the following would NOT be affected?
a.) The highest monthly rent
b.) The average monthly rent.
c.) The most frequent monthly rent.
d.) The spread of the monthly rents
Answers
The property that they would never be affected by is the most frequent monthly rent. Option C is correct.
Given that,
Kate collected a sample of monthly rents and recorded the following numbers: $500, $525, $550, $600, $600, $750, $775, $800, $1350. Kate drops the unusually high rent of $1350 from the data set, which of the following would not be affected is to be determined.
The statistic is the study of mathematics that deals with relations between comprehensive data.
Here,
If the rent of $1350 is dropped by Kate, definitely affect the average, highest monthly rent, and the spread of the monthly sheet, but it won't affect the most frequent monthly of rent because the most frequent rent is $600.
Thus, the property that they would never be affected by is the most frequent monthly rent. Option C is correct.
Learn more about Statistics here:
https://brainly.com/question/23091366
#SPJ5
The wedge is one-eighth of the wheel of cheese. A cylindrical-shaped wheel of cheese has a radius of 3 inches and height of 1 inch. A wedge of cheese is sliced from the whole. a. Find the surface area of the cheese before it is cut, round to the nearest hundredth. The surface area of the cheese before it is cut is in. $^2$ . b. Find the surface area of the remaining cheese after the wedge is removed, round to the nearest hundredth. The surface area of the remaining cheese after the wedge is removed is about square inches. Question 2 Did the surface area increase, decrease, or remain the same
Answers
Answer:
1. a. 75.39 in² b. 65.97 in²
2. Decreased
Step-by-step explanation:
1.
a. Find the surface area of the cheese before it is cut, round to the nearest hundredth.
Since the cheese is a cylinder with radius, r = 3 inches and height, h = 1 inch, its tital surface area, A = 2πr(r + h)
Substituting the values of the variables into the equation, we have
A = 2πr(r + h)
A = 2π(3 in)(3 in + 1 in)
A = (6π in)(4 in)
A = 24π in²
A = 75.39 in²
b. Find the surface area of the remaining cheese after the wedge is removed, round to the nearest hundredth.
Since the area of the wedge, A' is one-eight the area of the cheese, A
A'= A/8
= 75.39 in²/8
= 9.42 in²
The area of the remaining cheese is thus, area of cheese - area of wedge = A - A' = 75.39 in² - 9.42 in² = 65.97 in²
Question 2 - Did the surface area increase, decrease, or remain the same
Since the area of the remaining cheese, A' = 65.97 in² < A = 75.39 in², area of original cheese, the surface area decreased.
Brittany rents bicycles to tourists. She recorded the height (in cm) of each customer and the frame size (in cm) of the bicycle that customer rented. After plotting her results, Brittany noticed that the relationship between the two variables was fairly linear, so she used the data to calculate the following least squares regression equation for predicting bicycle frame size from the height of the customer: y=x+ What is the residual of a customer with a height of 155 cm who rents a bike with a 51 cm frame?
Answers
Answer: -1
Step-by-step explanation:
Here is the complete question:
Brittany rents bicycles to tourists. She recorded the height (in cm) of each customer and the frame size (in cm) of the bicycle that customer rented. After plotting her results, Brittany noticed that the relationship between the two variables was fairly linear, so she used the data to calculate the following least squares regression equation for predicting bicycle frame size from the height of the customer: y'=1/3x + 1/3.
What is the residual of a customer with a height of 155 cm who rents a bike with a 51 cm frame?
The regression equation is given as:
y'=(1/3)x + (1/3)
Since the height is given as 155cm, x=155 cm
The predicted frame size,
y'=(1/3)x + (1/3)
y'=(1/3) × 155+ (1/3)
= 51 2/3 + 1/3
= 52
The observed frame size,
y=51
Residual = Observed y- predicted y
=51-52
= -1
The residual of a customer with a height of 155 cm who rents a bike with a 51 cm frame is -1.
Answer:
-1
Step-by-step explanation:
