lan has $6,000. He wants to buy a car within $1,500 of this
amount. What is the price range of the car he wants to
purchase?
f. x2 $4,500 or x 2 $7,500 g. $4,500 2 x 2 $7,500
h. x < $4,500 or x = $7,500 j. $4,500 < x < $7,500
Answers
Answer: $7,500
Step-by-step explanation:
Related Questions
the top of a 13 foot ladder, leaning against a vertical wall, is slipping down the wall at the rate of 4 feet per second. how fast is the bottom of the ladder sliding along the ground away from the wall when the bottom of the ladder is 12 feet away from the base of the wall?
Answers
we know that
speed = distance/time
speed = dx/dt
Let x = the distance from the base of the ladder to the base of the wall
y = the distance from the tip of the ladder to the base of the wall, we have:
x^2+y^2 = 13^2
y^2=13^2-12^2 = 169 - 144 = 25 => y = 5 ft
2x dx/dt + 2y dy/dt = 0
2*5* dx/dt + 2*5*(-4) = 0
10 dx/dt = 40
dx/dt = (40/10) ft/sec
dx/dt = 4 ft/sec
To know more about
visit here
https://brainly.com/app/ask?q=speed
#SPJ4
Hello, I need some help, thx


Answers
Answer:
t=22 and j+10
Step-by-step explanation:
there were 22 students so t=22
10 people join the amount that were already there j+10
Answer:
First question: t = 22
Second question: j + 10
Step-by-step explanation:
First question: The last step tells us that there are a total of 22 people in the lunchroom. If t = total amount of people in the lunchroom than t would equal 22 according to the last step.
Second question: According to the third step, 10 students join the remaining students who are still in the lunch room. If j = students in the lunch before the 10 students join, then the expression or equation that represents the 10 students that join the lunchroom would be j + 10 because 10 students joined the students that were in the lunchroom before them.
Give a proof by contradiction that if 5n+4 is an odd integer then n is odd. Write out the statement you are using for proof by contradiction.
Answers
Therefore, if 5n + 4 is an odd integer, n must be odd. We will prove by contradiction that if 5n + 4 is an odd integer, then n must be odd.
To prove this statement by contradiction, we assume the opposite: that if 5n + 4 is an odd integer, then n is even. Suppose there exists an integer n such that 5n + 4 is an odd integer, but n is even.
If n is even, we can write it as n = 2k, where k is an integer. Substituting this into the equation 5n + 4, we get 5(2k) + 4 = 10k + 4. Now, let's assume that 10k + 4 is an odd integer.
An odd integer can be written in the form 2m + 1, where m is an integer. So, we have 10k + 4 = 2m + 1. Rearranging this equation, we get 10k = 2m - 3.
Now, notice that the left side of the equation is divisible by 2 since 10k is always even. However, the right side, 2m - 3, is an odd number (2m is even, and subtracting 3 from an even number results in an odd number). This creates a contradiction since an even number cannot be equal to an odd number.
Learn more about integer here:
https://brainly.com/question/490943
#SPJ11
A car travels 40 kph for 20 kilometers, 50 kph for 25 kilometers, 60 kph for 45 minutes and 48 kph for 15 minutes. What is the average speed of the car, in kph
Answers
The average speed of the car is 51 kph. The result is obtained by dividing the total distance by the total time taken.
What is average speed?Average speed is the overall speed of a moving object during a given amount of time. It can be expressed as
Avg speed = Total distance covered / Total time taken
The speed itself can be found by the following formula.
s = d/t
Where
s = speedd = distancet = timeA car can travel at the following speeds.
First lap with s₁ = 40 kph and d₁ = 20 km.Second lap with s₂ = 50 kph and d₂ = 25 km.Third lap with s₃ = 60 kph and t₃ = 45 minutes.Fourth lap with s₄ = 48 kph and t₄ = 15 minutes.Find the average speed!
We should convert the unit of time from minutes to hour.
t₃ = 45 minutes = ¾ h
t₄ = 15 minutes = ¼ h
We count the time and distance in each travels.
t₁ = d₁/s₁ = 20/40 = ½ h
t₂ = d₂/s₂ = 25/50 = ½ h
d₃ = s₃×t₃ = 60 × ¾ = 45 km
d₄ = s₄×t₄ = 48 × ¼ = 12 km
Avg speed = (s₁ + s₂ + s₃ + s₄)/(t₁ + t₂ + t₃ + t₄)
Avg speed = (40 + 50 + 60 + 48)/(½ + ½ + ¾ + ¼)
Avg speed = 102/2
Avg speed = 51 kph
Hence, the car has the average speed of 51 kph.
Learn more about average speed here:
brainly.com/question/17277454
#SPJ4
What is the volume of this sphere? Use : 3.14 and round your answer to the nearest hundredth. 16 ft cubic feet
Answers
According to the given graph, the diameter is 16 feet long, which means the radius is 8 feet.
Let's find the volume of the sphere using the proper formula
\(\begin{gathered} V=\frac{4}{3}\cdot\pi\cdot r^3 \\ V=\frac{4}{3}\cdot3.14\cdot(8ft)^3 \\ V\approx2,143.57ft^3 \end{gathered}\)Hence, the volume is 2,143.57 cubic feet.Out of a sample of 650 high school students, 321 take the bus to school every day. construct a 99% confidence interval for the population mean of high school students that take the bus to school every day.
Answers
The 99% confidence interval for the population mean of high school students who take the bus to school every day is approximately 0.445 to 0.543.
To construct a confidence interval for the population mean of high school students who take the bus to school every day, we can use the sample data and the formula for a confidence interval.
Given:
Sample size (n) = 650
Number of students who take the bus (x) = 321
To construct a 99% confidence interval, we need to determine the standard error and the critical value.
Step 1: Calculate the sample proportion (p-hat):
p-hat = x/n = 321/650 ≈ 0.494
Step 2: Calculate the standard error (SE):
SE = \(\sqrt{[(p-hat * (1 - p-hat)) / n]}\)
SE = \(\sqrt{[(0.494 * (1 - 0.494)) / 650]}\)
SE ≈ 0.019
Step 3: Determine the critical value (Z):
For a 99% confidence interval, the critical value is Z = 2.576 (from the standard normal distribution table).
Step 4: Calculate the margin of error (ME):
ME = Z * SE
ME ≈ 2.576 * 0.019 ≈ 0.049
Step 5: Calculate the confidence interval:
Lower bound = p-hat - ME
Upper bound = p-hat + ME
Lower bound ≈ 0.494 - 0.049 ≈ 0.445
Upper bound ≈ 0.494 + 0.049 ≈ 0.543
The 99% confidence interval for the population mean of high school students who take the bus to school every day is approximately 0.445 to 0.543. This means that we can be 99% confident that the true population mean lies within this interval.
To learn more about confidence interval visit:
brainly.com/question/29680703
#SPJ11
What is the solution to the trigonometric inequality sin(x) > cos(x) over the interval 0 ≤ x ≤ 2pi radians?
Answers
From the given information provided, the solution to the given trigonometric inequality is (π/4, 5π/4).
To solve the inequality sin(x) > cos(x) over the interval 0 ≤ x ≤ 2π radians, we can use the following steps:
Rewrite the inequality in terms of tangent:
Divide both sides by cos(x) to get:
tan(x) > 1
Find the solutions of the equation tan(x) = 1:
tan(x) = 1 when x = π/4 or x = 5π/4.
Check the sign of tangent in the intervals between the solutions:
We need to check the sign of tan(x) for x values in the following intervals:
(0, π/4), (π/4, 5π/4), and (5π/4, 2π).
In the interval (0, π/4), tan(x) is positive and less than 1.
In the interval (π/4, 5π/4), tan(x) is positive and greater than 1.
In the interval (5π/4, 2π), tan(x) is negative and less than -1.
Determine the solution set:
Since we are looking for x values that satisfy tan(x) > 1, the only interval that contains such values is (π/4, 5π/4). Therefore, the solution to the inequality sin(x) > cos(x) over the interval 0 ≤ x ≤ 2π radians is:
π/4 < x < 5π/4
In interval notation, we can write:
(π/4, 5π/4)
Learn more about inequality here: brainly.com/question/24372553
#SPJ4
For f(x)=x²−3, (a) calculate f(5x) and 5f(x) and (b)f(x−2) and f(x)−f(2).
Calculate the difference quotient of f(x)=−7x²−5x+9
Answers
a.
= (5x)² - 3 = 25x² - 3
- 5f(x) = 5(x² - 3) = 5x² - 15
b.
- f(x - 2) = (x - 2)² - 3 = x² - 4x + 1
- f(x) - f(2) = (x² - 3) - (2² - 3) = x² - 3 - 1 = x² - 4
a. To calculate f(5x), we substitute 5x into the function f(x) and simplify the expression.
f(5x) = (5x)² - 3 = 25x² - 3
To calculate 5f(x), we multiply the function f(x) by 5.
5f(x) = 5(x² - 3) = 5x² - 15
b. To calculate f(x - 2), we substitute (x - 2) into the function f(x) and simplify the expression.
f(x - 2) = (x - 2)² - 3 = x² - 4x + 4 - 3 = x² - 4x + 1
To calculate f(x) - f(2), we evaluate f(x) and f(2) separately and then find their difference.
f(x) = x² - 3
f(2) = 2² - 3 = 4 - 3 = 1
f(x) - f(2) = (x² - 3) - (2² - 3) = x² - 3 - 1 = x² - 4
For the difference quotient of f(x) = -7x² - 5x + 9, we can calculate it as follows:
Difference quotient = [f(x + h) - f(x)] / h
Expanding the function and substituting into the difference quotient formula, we have:
[f(x + h) - f(x)] / h = [-7(x + h)² - 5(x + h) + 9 - (-7x² - 5x + 9)] / h
Simplifying and expanding further:
= [-7(x² + 2hx + h²) - 5x - 5h + 9 + 7x² + 5x - 9] / h
= [-7x² - 14hx - 7h² - 5x - 5h + 9 + 7x² + 5x - 9] / h
= [-14hx - 7h² - 5h] / h
= -14x - 7h - 5
The difference quotient of f(x) = -7x² - 5x + 9 is -14x - 7h - 5.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
Using the binomial distribution, the probability that at least flights are on time is?
Answers
the probability that at least flights are on time is
P(7) + P(8) + P(9) + P(10)
To calculate the probability that at least a certain number of flights are on time using the binomial distribution, we need the probability of success (p), the number of trials (n), and the desired number of successful trials.
Let's assume we have the following information:
Probability of a flight being on time: p = 0.8 (80%)
Number of flights: n = 10
To find the probability that at least a certain number of flights are on time, we need to sum the probabilities of the desired number of successful trials and all higher numbers of successful trials.
Let's say we want to find the probability of at least 7 flights being on time.
P(at least 7 flights on time) = P(7) + P(8) + P(9) + P(10)
Using the binomial probability formula: P(x) = C(n, x) * p^x * (1-p)^(n-x)
where C(n, x) represents the number of combinations of n items taken x at a time.
Calculating the probabilities: P(7) = C(10, 7) * (0.8)^7 * (0.2)^(10-7) P(8) = C(10, 8) * (0.8)^8 * (0.2)^(10-8) P(9) = C(10, 9) * (0.8)^9 * (0.2)^(10-9) P(10) = C(10, 10) * (0.8)^10 * (0.2)^(10-10)
Finally, we sum up these probabilities to get the probability of at least 7 flights being on time.
P(at least 7 flights on time) = P(7) + P(8) + P(9) + P(10)
Performing the calculations will give us the specific probabilities and the final probability.
Complete Question :- According to an airline, flights on a certain route are on time 75% of the time. Suppose 24 flights are randomly selected and the number of on-time flights is recorded.
(a) Explain why this is a binomial experiment.
(b) Find and interpret the probability that exactly 14 flights are on time.
(c) Find and interpret the probability that fewer than 14 flights are on time.
(d) Find and interpret the probability that at least 14 flights are on time.
(e) Find and interpret the probability that between 12 and 14 flights, inclusive, are on time.
To know more about probability, visit
https://brainly.com/question/31828911
#SPJ11
Both 2 and x are polynomials. The product of 2 and x Response area a polynomial. The quotient of 2 and x Response area a polynomial. The quotient of x and 2 Response area a polynomial.
Answers
Yes, both 2 and x are polynomials. A polynomial is any expression that consists of variables, coefficients, and non-negative integer exponents.
What is variables?A variable is a named storage location used to store a value that can be changed during the execution of a program. Variables are typically used to store values that are entered by a user or used to store the results of calculations or operations. Variables can be declared with different data types, such as strings, integers, or decimals, and can be given a name to be used when referring to the value stored in the variable.
That can be written in the form \(\mathrm a_nx^n + a_n-1x^n-1 + ... + a_2x^2 + a_1x + a_0\).
The product of 2 and x is also a polynomial because it is the result of multiplying two polynomials together. The product of 2 and x is 2x, and this can be written in polynomial form as 2x¹.
The quotient of 2 and x is also a polynomial, since a polynomial can also be written in fractional form. The quotient of 2 and x can be written as 2/x, which is a polynomial with coefficients of 2 and -1 and an exponent of 0.
To learn more about variables
brainly.com/question/2804470
#SPJ1
This will be question that pulls in a lot of parts of this course. So, consider the following economy: Suppose that the production function for the economy is given by: Y=AL
2
/3K
1/3
Suppose that this economy has 1,000 units of Labour, and 125 units of capital, and TFP (A) is equal to 10. The Short-Run Aggregate Supply Curve (AS) here is given by: Y=5p And when we consider the AEF at a price level of $1,400, the main components of it (C,I,&G) are given by (we are assuming a closed economy NX=0 ): C=300+0.8Y
I=300
G=200
1. What is potential GDP in this question (Y
∗
) ? Show your work. [2 points] Suppose also that for any $10 decrease in price, desired consumption will increase by $5. 2. Write down the equation for the Aggregate Demand Curve (AD) in the form of Y=a+bp. Show your work. [3 points] 3. What is the current Short-Run Equilibrium value for Real GDP (Y) and the price level (p)? Show your work. [2 points] 4. Draw the AD, AS, and LRAS curves. Label all x-intercepts and y-intercepts. Are we currently in an Inflationary Gap, Recessionary Gap, or in Long-Run Equilibrium? How do you know? [4 points] Now suppose that the Central Bank has set the current Money Supply to be equal to $8,000. This Money Supply is currently made up of $2,000 of printed currency, and $6,000 of Bank Deposits. The current mandated reserve ratio is 10%. The Demand for Money (MD) as a function of the interest rate ( " i ") is given by: MD=20,000−1,000i Note that we are assuming that this MD curve does not shift with changes in p or Y in the economy. 5. Draw the MS and MD curves in a single figure. Label all x-intercepts and y-intercepts. Where is the equilibrium in the money market? Given this, what is the current prevailing market interest rate (i
∗
) ? [4 points] Now suppose that there is an increase in autonomous consumption of 180. 6. What will be the new short-run equilibrium Real GDP in this case? Are we in an inflationary gap or recessionary gap now? How large is it? Show your work. [4 points] Finally, suppose that for every 1% decrease in the interest rate, Desired Consumption will increase by $25 and Desired Investment will increase by $25. The Central Bank wants to close this output gap. 7. If the Central Bank wants to close this gap by changing the Money Supply in circulation, how much does the MS need to change to close this gap? What is the new interest rate? Show your work. [4 points] 8. Suppose instead that the Central Bank wants to reduce the money supply by raising reserve requirements instead. How much does it need to raise the reserve requirements to close this gap? Show your work. [3 points] For the purposes of the next questions, the First MD Curve is as before: MD=20,000−1,000i And the Second MD curve a new MD curve: MD=20,000−400i In the case of the Second MD curve, also assume that the Money Supply begins at 15,200. (So we start at the same interest rate in each case). Note that once again, these MD curves are assumed to not vary with p or Y in the economy, despite the theory we covered in lecture. This is for mathematical convenience. 9. With the Second MD Curve, would the Central Bank need to change the Money Supply by more or less than it would with the First MD Curve if it wanted to close this inflationary gap? Explain your answer. [2 points] 10. Which of the two curves would Keynesians believe is more likely to be the case? Which is more in line with the monetarist point of view? Explain your answer. [2 points]
Answers
1. To find the potential GDP (Y*), we substitute the given values into the production function:
Y = AL^(2/3)K^(1/3)
Y* = A(1000)^(2/3)(125)^(1/3)
Y* = 10(1000)^(2/3)(125)^(1/3)
Y* = 10(10^2)(5)
Y* = 50,000
2. The equation for the Aggregate Demand Curve (AD) in the form of Y = a + bp can be derived from the given information. Since we know that the main components of Aggregate Expenditure Function (AEF) are:
C = 300 + 0.8Y
I = 300
G = 200
And we assume a closed economy with NX = 0, the equation for AD becomes:
Y = C + I + G
Y = (300 + 0.8Y) + 300 + 200
Y = 800 + 0.8Y
0.2Y = 800
Y = 4000 + 5p
3. To find the current Short-Run Equilibrium value for Real GDP (Y) and the price level (p), we set AD equal to AS:
4000 + 5p = 5p
4000 = 0
Since the equation does not hold true, there is no short-run equilibrium value for Y and p based on the given information.
4. In the graph, the Aggregate Demand (AD), Short-Run Aggregate Supply (AS), and Long-Run Aggregate Supply (LRAS) curves will be represented. The x-intercept of AD indicates potential GDP, and the intersection of AD and AS determines the short-run equilibrium. If the short-run equilibrium is to the right of potential GDP, it indicates an inflationary gap. If it's to the left, it indicates a recessionary gap. If the short-run equilibrium coincides with potential GDP, it represents long-run equilibrium.
(Note: As a text-based AI, I'm unable to draw the graph here, but you can plot it on a graph paper or use a graphing tool to visualize it based on the given equations.)
5. Drawing the MS (Money Supply) and MD (Money Demand) curves, we have:
MS: $8,000
MD: 20,000 - 1,000i
The equilibrium in the money market occurs where the MS and MD curves intersect. The prevailing market interest rate (i*) is determined by the point of intersection.
6. With an increase in autonomous consumption of 180, the new short-run equilibrium Real GDP will be determined by adjusting the consumption component in the AD equation:
Y = (300 + 0.8(180 + Y)) + 300 + 200
Solving for Y, we find the new short-run equilibrium Real GDP.
7. To close the output gap by changing the Money Supply (MS), we need to determine the change in MS required to achieve the desired level of Real GDP. This can be calculated by adjusting the MS until the short-run equilibrium reaches the desired Real GDP. The new interest rate can also be calculated based on the changes in MS.
8. If the Central Bank wants to reduce the money supply by raising reserve requirements instead, the amount by which the reserve requirements need to be raised can be calculated to achieve the desired level of Real GDP. This can be done by adjusting the reserve ratio until the short-run equilibrium reaches the desired Real GDP.
9. With the Second MD Curve (MD = 20,000 - 400i), the Central Bank would need to change the Money Supply by a different amount compared to the First MD Curve (MD = 20,000 - 1,000i) to close the inflationary gap. This is because the slopes of the two MD curves are different, resulting in different changes in the equilibrium interest rate and Money Supply.
10. Keynesians are more likely to believe that the First MD Curve (MD = 20,000 - 1,000i) is more likely to be the case. This is because Keynesian economics emphasizes the role of fiscal policy and government intervention in managing the economy. On the other hand, the First MD Curve is more in line with the monetarist point of view, which focuses on the control of money supply and the importance of monetary policy in economic management.
To learn more about GDP
https://brainly.com/question/30109046
#SPJ11
Please answer this big question nobody ever answers my questions im sad :(

Answers
Answer:
Step-by-step explanation:
1.
3,4,5 will make a triangle.
2.
sum of any sides > third side
difference of any two sides < third side
3+4=7>5
4+5=9>3
5+3=8>4
again
4-3=1<5
5-3=2<4
5-4=1<3
so it makes one triangle.
3.
3,4,8
4.
3+4=7 not >7
again
8-4 =4 not <3
so they do not make a triangle.
HELPPPP
FRACTION HAS TO BE IN DECMAL
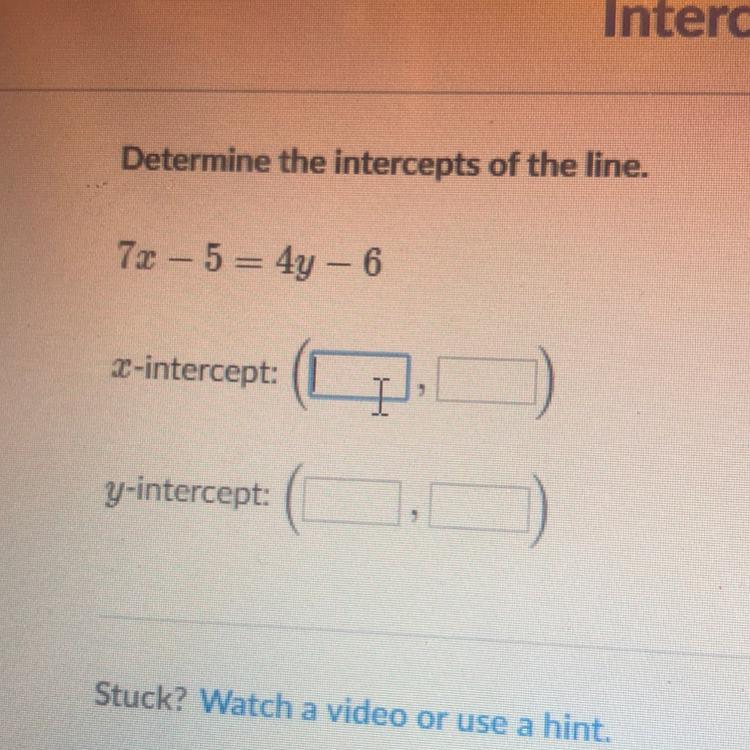
Answers
Answer:
x intercept: (-1/7, 0) or (.14, 0)
y intercept: (0, 1/4) or (0, .25)
Step-by-step explanation:
Answer:
x- (−0.142857142857143,0)
y- (0, .25)
Step-by-step explanation:
The x-intercept:
Plug y=0 into the equation and solve the resulting equation 7x−5=−6 for x
(−1/7,0) = (−0.142857142857143,0)
The y-intercept:
Plug x=0 into the equation and solve the resulting equation −5=4y−6 for y
(0,1/4) = (0, .25)
Economists have found that the amount of corruption in a country's government is correlated to the gross domestic product (gdp) per capita of that country. this can be modeled by y=507x−8030 where x is the corruption score and y is gdp per capita in dollars. corruption scores range from 0 to 100 with 0 being highly corrupt and 100 being least corrupt. using this model, a country with a corruption score of 99 would have what gdp per capita? round your answer to the nearest dollar.
Answers
According to the given model, a country with a corruption score of 99 would have a GDP per capita of approximately $41,657.
The given model, y = 507x - 8030, represents the correlation between the corruption score (x) and GDP per capita (y) of a country.
To find the GDP per capita for a corruption score of 99, we substitute x = 99 into the equation. Thus, y = 507(99) - 8030.
Solving this equation, we get y = 49893, which represents the GDP per capita in dollars. To round this value to the nearest dollar, we consider the decimal part of the number. Since the decimal part is greater than or equal to 0.5, we round the whole number up.
Therefore, the GDP per capita for a country with a corruption score of 99 would be approximately $41,657.
To know more about whole number visit:
https://brainly.com/question/29766862
#SPJ11
How do you find the midpoint of coordinates
Answers
Answer:
The midpoint is halfway between two end points.
The x value is halfway between the two x values and
the y value is also halfway between the two y values.
Add both the x and y coordinates and divide by 2.
Step-by-step explanation:
To find the x-coordinate of the midpoint of a segment, add the x-coordinates of the endpoints and divide by 2.
To find the y-coordinate of the midpoint of a segment, add the y-coordinates of the endpoints and divide by 2.
Example:
Find the midpoint of the segment with endpoints (2, 8) and (-5, 12).
x-coordinate of the midpoint: (2 + (-5))/2 = -3/2
y-coordinate: (8 + 12)/2 = 30/2 = 15
Midpoint: (-3/2, 15)
Luca Is putting cookles Into bags. She has 35 cookies. She wants to put 3 cookles In each bag. She divides to find out how many bags she can till.
35 ÷ 3 = 11 r2
What does the answer mean?
Answers
Answer:
D.
35 ÷ 3 = 11.7
3 x 11 = 33
35 - 33 = 2
She can fill 11 bags and have 2 left over.
Step-by-step explanation:
Answer: 35/3
Step-by-step explanation:
R-squared is a statistical measure that represents the proportion of the variance for a dependent variable that's explained by an independent variable.
What is 186 cm in feet?
Answers
186 cm is equivalent to approximately 6.1023 feet.
The conversion factor for centimeters to feet is that 1 cm is equal to 0.0328084 feet. To convert centimeters to feet, you multiply the number of centimeters by 0.0328084. In this case, 186 x 0.0328084 = 6.1023 feet. It's important to note that while centimeters and feet are both units of measurement for length, they are not interchangeable and are used in different parts of the world.
Centimeters are widely used in the metric system, which is used by most of the countries in the world, while feet are used in the imperial system which is used in some countries such as the United States, United Kingdom and others who adopted the imperial system.
To know more about conversion factor click on the link below:
https://brainly.com/question/30166433#
#SPJ11
The price of 4 donuts and 2 croissants is $10. The price of 2 donuts and 3 croissants is $9. How much does 1 donut and 1 croissant cost?
Answers
Answer:
1 donut =1.50$ 1 croissant = 2$
Triangle ABC is congruent to triangle DEF. Select all the statements that are a result of corresponding parts of congruent triangles being congruent.

Answers
Segment BC is congruent to segment EF,
Angle BAC is congruent to angle EDF,
Angle CBA is congruent to angle DEF.
Given:
Triangle ABC is congruent to triangle DEF.
if two triangles are congruent:
congruent sides are:
AB ↔ DE ,BC↔EF, CA ↔ FD
congruent angles are:
<A ↔ <D , <B ↔ <E, <C ↔ <F.
Therefore Segment BC is congruent to segment EF, Angle BAC is congruent to angle EDF, Angle CBA is congruent to angle DEF are correct.
Learn more about the triangles here:
https://brainly.com/question/2773823
#SPJ1
Thirty percent of what number is 13.5?
Answers
Answer:
Well we can take this word for word into an expression
thirty percent of which is basically
0.3 *
We have an unknown number (what number) lets make that unknown number x
0.3 * x
And we want to know what is 13.5 which basically means equal 13.5
0.3 * x = 13.5
We solve for x
Solve from here.
I’m gonna multiply 10 on both sides
3 * x = 135
Now solve
x = 45
no.8
8. Find the geometric mean radius of the unconventional conductors in terms of the radius r of an individual strand. A. 1.074r C. 1.402r D. 1.953r ooo B. 1.583r
Answers
The geometric mean radius of the unconventional conductors in terms of the radius r of an individual strand is 1.583r.
To find the geometric mean radius of the unconventional conductors, we need to understand the concept of geometric mean. The geometric mean of two numbers is the square root of their product. In this case, we are looking for the geometric mean radius of multiple strands.
First, we need to determine the number of strands in the unconventional conductors. The question does not provide this information explicitly, so we assume there are at least two strands.
We know that the geometric mean radius is the square root of the product of the individual strand radii. Let's assume there are n strands, and the radius of each strand is r. Therefore, the product of the individual strand radii would be r^n.
Now, we can calculate the geometric mean radius by taking the square root of r^n. Mathematically, it can be expressed as (r^n)^(1/n) = r^((n/n)^(1/n)) = r^1 = r.
Therefore, the geometric mean radius in terms of the radius r of an individual strand is 1.583r.
Learn more about
#SPJ11
what is the answer to this promblem

Answers
9514 1404 393
Answer:
to eliminate x: multiply the first by 3, and the second by -4to eliminate y: multiply the first by 2, and the second by 5Step-by-step explanation:
Pick the variable you want to eliminate. Determine the coefficients of that variable in the two equations. Negate one of them. Multiply each equation by the coefficient that came from the other equation.
__
To eliminate x
The x-coefficients are 4 and 3. If we negate 4, then the resulting y-coefficient will be positive. We choose to multiply the first equation by 3, the second by -4.
Here is the result of adding those:
3(4x +5y) -4(3x -2y) = 3(7) -4(-12) ⇒ 23y = 69
To eliminate y
The y-coefficients are 5 and -2. If we negate -2, then the resulting x-coefficient will be positive. We choose to multiply the first equation by 2 and the second by 5.
Here is the result of adding those:
2(4x +5y) +5(3x -2y) = 2(7) +5(-12) ⇒ 23x = -46
Answer:
Step-by-step explanation:
to kill x: duplicate the primary by 3, and the moment by -4 to eliminate y: increase the primary by 2, and the moment by 5 Step-by-step explanation: Pick the variable you need to eliminate. Decide the coefficients of that variable within the two conditions. Refute one of them. Increase each condition by the coefficient that came from the other equation. __ To dispense with x The x-coefficients are 4 and 3. On the off chance that we invalidate 4, then the coming about y-coefficient will be positive. We select to increase the primary condition by 3, the moment by -4. Here is the result of including those: 3(4x +5y) -4(3x -2y) = 3(7) -4(-12) ⇒ 23y = 69 To dispose of y The y-coefficients are 5 and -2. If we nullify -2, at that point the coming about x-coefficient will be positive. We select to duplicate the primary condition by 2 and the moment by 5. Here is the result of including those: 2(4x +5y) +5(3x -2y) = 2(7) +5(-12) ⇒ 23x = -46
hope this helps
Pizza Hut charges $10 per large pizza plus a $4 delivery fee. If you spent a total of $34, how many pizzas did you order
Answers
Answer:
3 pizzas
Step-by-step explanation:
34-4=30
30/10=3
Answer:
3 pizzas
Step-by-step explanation:
34-4=30 since we already know the delivery fee
30/10=3 since we have 30 dollars left without the delivery fee we are just left to divide 30 by 10 to get the total number of pizzas
A shoemaker sold a pair of for $245.99 if the buyer a $300.00 bill, how much will the buyer receive in change?
*two decimal places don't forget your $ sign. Example: $50.00 NOT 50*
Answers
Answer:
$54.01
Step-by-step explanation:
All you have to do is $300.00-$245.99 .
mt. everest is approximately 8849m in height. what would be the weight of an 85kg man at its summit?
Answers
The weight of the man at the summit of Mt. Everest is 833 kg·m/s^2
The weight of an 85kg man at the summit of Mt. Everest can be calculated using the formula: Weight = mass × acceleration due to gravity.
The acceleration due to gravity is approximately 9.8 m/s^2. Therefore,
In terms of units, this can also be expressed as 833 Newtons (N). The weight represents the force with which the man is pulled towards the center of the Earth.
The weight of an object is directly proportional to its mass. In this case, the mass of the man is given as 85kg. By multiplying the mass by the acceleration due to gravity, we can calculate the weight of the man at the summit of Mt. Everest.
It's important to note that the weight of an object can vary depending on the location due to the variation in the acceleration due to gravity at different elevations. At higher altitudes, such as the summit of Mt. Everest, the acceleration due to gravity is slightly lower than at sea level. However, for this calculation, we have used the standard acceleration due to gravity of approximately 9.8 m/s^2 for simplicity.
Learn more about acceleration here:
https://brainly.com/question/2303856
#SPJ11
Which one of the choices below represents the preferred practice regarding significant figures when multiplying the following: 20.6×5.5×6.27 ? (a) 710.391 (b) 710 (c) 710.3 (d) 710.4 Q2. Given two vectors,
A
=2
−3
+7
k
and
B
=5
+
+2
k
, find (a) ∣
A
∣ and ∣
B
∣ (b)
A
+
B
(c)
A
−
B
Q3.state whether each expression is meaningful. If not, explain why. If so, state whether it is a vector or a scalar. a. a⋅(b×c) b. a×(b⋅c) c. a×(b×c) d. (a⋅b)×c e. (a⋅b)×(c⋅d) f. (a×b)⋅(c×d) Q4. Using the cross product of vectors, can you answer the following question: Is the line through (−4,−6,1) and (−2,0,−3) parallel to the line through (10,18,4) and (5,3,14) ?
Answers
(1) The significant figure will be 710.
Hence the correct option is (b).
(2) (a) The modulus of A and B are,
| A | = √62
| B | = √30
(b) The value of A + B = 7 i - 2 j + 9 k
(c) The value of A - B = -3 i - 4 j + 5 k
(3) (a) a ⋅ (b × c) is meaningful and result is a scalar.
(b) a × (b ⋅ c) is not meaningful.
(c) a × (b × c) is meaningful and result is a vector.
(d) (a ⋅ b) × c is not meaningful.
(e) (a ⋅ b) × (c ⋅ d) is not meaningful.
(f) (a × b) ⋅ (c × d) is meaningful and result is a scalar.
The not meaningful is because to conduct cross product we need two vectors.
(4) Given lines are parallel because the cross product of the vectors along that lines is zero vector.
(1) Given the multiplication is,
20.6 × 5.5 × 6.27
That gives the result,
20.6 × 5.5 × 6.27 = 710.391
Here significant figure will be 710.
So the correct option is (b).
(2) Given the vectors are,
A = 2 i - 3 j + 7 k
B = 5 i + j + 2 k
(a) The modulus of A and B are,
| A | = √[2² + (-3)² + 7²] = √62
| B | = √[5² + 1² + 2²] = √30
(b) The value of A + B vector is,
A + B = [2 i - 3 j + 7 k] + [5 i + j + 2 k] = 7 i - 2 j + 9 k
(c) The value of A - B vector is,
A - B = [2 i - 3 j + 7 k] - [5 i + j + 2 k] = -3 i - 4 j + 5 k
(3) We know that the cross product gives vector result and dot product gives scalar result.
The statements are,
(a) a ⋅ (b × c) is meaningful and result is a scalar.
(b) a × (b ⋅ c) is not meaningful.
(c) a × (b × c) is meaningful and result is a vector.
(d) (a ⋅ b) × c is not meaningful.
(e) (a ⋅ b) × (c ⋅ d) is not meaningful.
(f) (a × b) ⋅ (c × d) is meaningful and result is a scalar.
The not meaningful is because to conduct cross product we need two vectors.
(4) Here for first line vector is,
A = [(-2) - (-4)] i + [0 - (-6)] j + [(-3) - 1] k = 2 i + 6 j - 4 k
for second line vector is,
B = [5 - 10] i + [3 - 18] j + [14 - 4] k = -5 i - 15 j + 10 k
So now the cross product is,
A × B = \(\left[\begin{array}{ccc}i&j&k\\2&6&-4\\-5&-15&10\end{array}\right]\) = 0 i + 0 j + 0 k
So the cross vector is a zero vector so the initial vectors are parallel to each other.
To know more about vectors here
https://brainly.com/question/2005068
#SPJ4
if v=5 x=38 and y=-7 find w
Answers
Answer:
incomplete question friend
Determine where are each piece below blogs to create a rational expression equivalent to the one shown above

Answers
We can write the above expression as
\(\frac{5x^2+25x+20}{7x}=\frac{5(x^2+5x+4)}{7x}=\frac{5(x+1)(x+4)}{7x}\)Now we know that
\(x^2+2x+1=(x+1)^2\)And
\(7x^2+x=7x(x+1)\)Also for the piece
\(5x^2+15x-20=5(x^2+3x-4)=5(x-1)(x+4)\)So we shall use
\(5x^2+15-20\text{ }\)And
\(x-1\text{ }\)To fill the blanks so that this expression will be similar to the above.
\(\frac{x^2+2x+1}{x-1}\times\frac{5x^2+15x-20}{7x^2+x}=\frac{(x+1)^2}{x-1}\times\frac{5(x-1)(x+4)_{}}{7x(x+1)}=\frac{x+1}{1}\times\frac{5(x+4)}{7x}=\frac{5(x+1)(x+4)}{7x}\)The principal wants to share 1,869 pencils equally between 4 fourth grade classrooms and 3 third grade classrooms. how many pencils will each classroom get?
Answers
Goode Manufacturing pays Betty Robert's a $1770 monthly salary plus a 14% commission on merchandise she sells each month. assume Betty's sales were $99,200 for last month. calculate the following amounts: 1.amount of commission? gross pay?
Answers
Given:
Betty's monthly salary = $1770
Commision on sales = 14%
Betty sales for last month = $99,200
1. The amount of commission is 14% of $99,200.
Therefore, we have:
\(\frac{14}{100}\times99200=0.14\times99200=\text{ \$13888}\)The amount of commission is $13,888
2. The gross pay.
Gross pay is the amount Betty receives before taxes and deductions.
Gross pay = Salary + Commission
Thus, the gross pay is:
$13888 + $1770 = $15,658
ANSWER:
1. Commission = $13,888
2. Gross pay = $15,658