PLEASE HELP !! ILL GIVE BRAINLIEST *EXTRA POINTS*..
IM GIVING 40 POINTS !! DONT SKIP :((.

Answers
Answer:
y = 1x - 25
Step-by-step explanation:
Related Questions
find the value of this expression is x=1
x^2+4/x-6
Answers
5/-5
the answer is -1
Answer:
x
−
3
x
−
2
Step-by-step explanation:
1. The ratio of faculty members to students at a college is 1:18. If there are 16000 students, how many faculty members are there? Round to the nearest whole number
Answers
Therefore, there are approximately 889 faculty members at the college.
What is ratio?Ratio is a mathematical concept that expresses the relationship between two or more quantities or values. It is a way to compare the size of two numbers, by dividing one number by the other. The result of this division is a numerical expression of the relative size of the two numbers.
Ratios are often expressed as a fraction or a colon (:) between the two numbers. For example, if there are 4 red balls and 6 blue balls in a bag, the ratio of red balls to blue balls can be expressed as 4/6 or 4:6. This means that for every 4 red balls in the bag, there are 6 blue balls.
Ratios are commonly used in various fields, such as finance, statistics, and science, to compare different values and make meaningful interpretations.
To solve this problem, we need to use the ratio between faculty members and students, which is given as 1:18. This means that for every one faculty member, there are 18 students.
If there are 16000 students in the college, we can find the number of faculty members by dividing the number of students by the ratio of students to faculty members:
Number of faculty members = 16000 / 18
This gives us 888.888, but since we are asked to round to the nearest whole number, we should round up to 889. Therefore, there are approximately 889 faculty members at the college.
To know more about number visit:
https://brainly.com/question/17429689
#SPJ1
For which inequality is X= 5 a solution?
Answers
x+7>=12
Hope this helps?
Can you mark my answer as brainliest please?
The average number of tunnel construction projects that take place at any one time in a certain state is 3. Find the probability of exactly five tunnel construction projects taking place in this state.
Answers
Answer: 0.1008188
Step-by-step explanation:
The question will usng the poisson distribution formula:
Given :
Mean(λ) number of occurrence in a given interval = 3
P(X=x) = Probability of exactly x occurrence in a given interval
Number of desired occurence(x) = 5
P(X=x) = [(λ^x) * (e^-λ)] / x!
Where ; e = base of natural logarithm = 2.7182818
P(X=5) = [(3^5) * (e^-3)] / 5!
P(X=5) = [(243) * (0.0497870)] / 120
P(X=5) = [12.098257] / 120
P(X=5) = 0.1008188
Answer:0.10
Step-by-step explanation:
3/4 divided by 1/2 please hurry !!
Answers
Answer:
3/2 or 1.5
Step-by-step explanation:
(3/4) / (1/2) = (3/4) * (2/1)
= 6/4
= 3/2
It is given that,
→ 3/4 ÷ 1/2
We can divide the given values,
→ 3/4 ÷ 1/2
→ 3/4 × 2/1
→ 6/4
→ 3/2 (or) 1.5
Thus, 3/2 (or) 1.5 is the answer.
Given sinz = -4/5 for pi < z < (3pi)/2, find the value of cosz.

Answers
The angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
Given sinz = -4/5 for pi < z < (3pi)/2, we need to find the value of cosz. We can use the trigonometric identity of Pythagorean theorem to find the value of cosz.
According to Pythagorean theorem, sin2θ + cos2θ = 1, where θ is the angle in the right-angled triangle and sin, cos are the trigonometric ratios.
The negative sign for the given sinz indicates that the angle z is in the third quadrant. So, we can take the help of the unit circle to find the value of cosz as shown below:
Here, we have used the Pythagorean identity of sin2z + cos2z = 1 on the unit circle to find the value of cosz. Since the value of sinz is already given, we can find the value of sin2z as: sin2z = sinz x sinz = (-4/5) x (-4/5) = 16/25
Then, we can substitute the value of sin2z in the Pythagorean identity as: cos2z = 1 - sin2z = 1 - (16/25) = 9/25We need to find the value of cosz.
So, we can take the square root of cos2z as: cosz = ±(√(9/25)) = ±(3/5)The sign of cosz can be determined by considering the quadrant of the angle z.
Since the angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
For more questions on angle.
https://brainly.com/question/31615777
#SPJ8
You deposit $300 in an account that earns simple interest at an annual rate of 6.5%.
If no other deposits or withdrawals were made, what is the total amount of money in the account at the end of 8 years?
Answers
Total amount of money in the account will be $456.
How much money will be in the account after 8 years?Simple interest is an interest charge that borrowers pay lenders for a loan. It is calculated using the principal only and does not include compounding interest.
The formula for simple interest is: Simple Interest = Principal × Rate × Time
Principal (P) is $300
Rate (R) is 6.5%
Time (T) is 8 years.
Simple Interest = $300 × 0.065 × 8
Simple Interest = $156
Total Amount = Principal + Simple Interest
Total Amount = $300 + $156
Total Amount = $456.
Read more about simple interest
brainly.com/question/25793394
#SPJ1
i need the answer to this question

Answers
Answer:
Area of annulus is 40.85cm² to 2d.p
Step-by-step explanation:
Area of shaded part=Area of bigger circle -Area of smaler circle
Area of annulus= πR²- πr²= π(R²-r²)
A=3.142(7²-6²)
A=3.142(49-36)
A=3.142×13
A=40.846cm²
A=40.85cm² to 2d.p
3 9/13 to a improper fraction
Answers
Answer:
48/13
Step-by-step explanation:
To make this into an improper fraction, convert the integer into a fraction using the denominator of the fraction
3 * 13/13 = 39/13
Then add it to the rest of the fraction
39/13 + 9/13
= 48/13
Answer: 48/13
Step-by-step explanation: first multiply 3 x 13 to get 39. do this because you get the fraction for the whole number, 3. then, add 39 to the numerator (9). you will get 48/13. you do this because you are adding the whole number (3) to the fraction so that way it is an improper fraction.
What the meaning of statement this?

Answers
The statement is asserting that the universal class (V) is defined as the collection of all sets, where every set is included. It signifies that V encompasses all possible sets within the given set theory framework.
The statement "The universal class set, or universe, is the class of all sets: V = {x: x = x}" is referring to the concept of the universal class or the universe in set theory.
In set theory, the universal class set, denoted as V, represents the collection or class that contains all sets. It includes every possible set that can be defined or exists within the context of the set theory being considered.
The notation "{x: x = x}" is used to define the elements of the universal class. Here, "x = x" represents a condition that is always true for any object or element, regardless of its nature. In other words, this condition holds for everything in the universe, as anything is equal to itself.
Learn more about sets here:
https://brainly.com/question/30705181
#SPJ1
what is the biggest decimal and take away two
Answers
Answer:
about -1
Step-by-step explanation:
0.9999999999 minus 2
The equation of a circle is:
(x-2)^2 + (y+4)^2 = 25
Part A:
Determine the center and the radius of the circle.
...is this correct?

Answers
The requried center and radius of the given circle are (2, -4) and 5.
The standard equation of a circle is given as,
(x - h)² + (y - k)² = r²
Where, (h, k) is the center of the circles and r is the radius of the circle,
The equation of the given circle is,
(x - 2)² + (y + 4)² = 25
Comparing the above equation with the standard equation we have,
(h, k) = (2, -4)
r² = 5²; r =5
Thus, the requried center and radius of the given circle is (2, -4) and 5.
Learn more about Circle here:
https://brainly.com/question/29288238
#SPJ1
Please look at the photo. Thank you.

Answers
The output value of (f∘g)(x) is: \((f \circ g)(x) = \frac{4x^2-29x+60}{x +3}\)
The domain of (f∘g)(x) is (-∞, -3) U (-3, ∞).
How to determine the corresponding output value for this function?In this scenario, we would determine the corresponding composite function of f(x) and g(x) under the given mathematical operations (multiplication) in simplified form as follows;
\(f(x) = \frac{x-6}{x +3}\)
g(x) = 4x - 15
Next, we would write the numerators and denominators in factored form as follows;
(x - 6)(4x - 15)
4x² - 15x - 24x + 60
4x² - 29x + 60
Now, we can derive the corresponding composite function of f(x) and g(x);
\((f \circ g)(x) = \frac{4x^2-29x+60}{x +3}\)
For the restrictions on the domain, we would have to equate the denominator of the rational function to zero and then evaluate as follows;
x + 3 ≠ 0
x ≠ -3
Domain = (-∞, -3) U (-3, ∞).
Read more on domain here: brainly.com/question/17440903
#SPJ1
Analyze the diagram below and complete the instructions that follow.
а
60°
b.
45°
8
Find a, b, and c.

Answers
Answer:
c:x=6√3,y=12
Step-by-step explanation:
the shape
Answer:
C
Step-by-step explanation:
The base angles are congruent, both 60°, thus the triangle is isosceles and x is a perpendicular bisector ( divides the base into 6 and 6 )
Using the tangent ratio in the right triangle on the left and exact value
tan60° = \(\sqrt{3}\) , then
tan60° = \(\frac{opposite}{adjacent}\) = \(\frac{x}{6}\) ( multiply both sides by 6 )
6 × tan60° = x , that is
x = 6\(\sqrt{3}\)
Using the cosine ratio in the same right triangle and exact value
cos60 = \(\frac{1}{2}\) , then
cos60° = \(\frac{adjacent}{hypotenuse}\) = \(\frac{6}{y}\) ( multiply both sides by y )
y × cos60° = 6 , that is
y × \(\frac{1}{2}\) = 6 ( multiply both sides by 2 )
y = 12
Integrate :
\(\red{\footnotesize\displaystyle\bf \int cos^3 4x\:\:dx}\)
Answers
Recall the half-angle identity for cosine:
cos²(x) = 1/2 (1 + cos(2x))
Then we can rewrite the integrand as
cos³(4x) = cos(4x) cos²(4x) = 1/2 cos(4x) (1 + cos(8x))
So we have
\(\displaystyle \int \cos^3(4x) \, dx = \frac12 \int (\cos(4x) + \cos(4x)\cos(8x)) \, dx\)
Next, recall the cosine product identity,
cos(a) cos(b) = 1/2 (cos(a - b) + cos(a + b))
so that the integral is equivalent to
\(\displaystyle \int \cos^3(4x) \, dx = \frac12 \int \cos(4x) \, dx + \frac14 \int (\cos(4x - 8x) + \cos(4x + 8x)) \, dx\)
\(\displaystyle \int \cos^3(4x) \, dx = \frac34 \int \cos(4x) \, dx + \frac14 \int \cos(12x) \, dx\)
Computing the rest is trivial:
\(\displaystyle \int \cos^3(4x) \, dx = \boxed{\frac3{16} \sin(4x) + \frac1{48} \sin(4x) + C}\)
Please help me answer this question!!!!

Answers
9514 1404 393
Answer:
y = 4x +3
Step-by-step explanation:
The slope formula can be used to find the slope:
m = (y2 -y1)/(x2 -x1)
Using the first two lines of the table, we find the slope to be ...
m = (11 -7)/(2 -1) = 4/1 = 4
__
The y-intercept can be found from the relation ...
b = y -mx
Using the slope we found, and the first line of the table, we find the intercept to be ...
b = 7 -4(1) = 3
__
Then the equation is ...
y = mx +b . . . . . . slope-intercept form of the equation for a line
y = 4x +3
Can someone help find the surface area, then round the answer to the nearest whole number please?

Answers
The Surface Area of cylinders are: 100 yd² , 264 m², 226 mm²
The Surface Area of Can is 219 cm².
We know the formula for Surface Area of Cylinder
= 2πrh
1. Radius = 2 yd
Height = 8 yd
So, Surface Area of Cylinder
= 2πrh
= 2 x 3.14 x 2 x 8
= 100 yd²
2. Radius = 7 m
Height = 6 m
So, Surface Area of Cylinder
= 2πrh
= 2 x 3.14 x 6 x 7
= 264 m²
3. Radius = 3 mm
Height = 12 mm
So, Surface Area of Cylinder
= 2πrh
= 2 x 3.14 x 3 x 12
= 226 mm²
4. Radius = 3.5 cm
Height = 10 cm
So, Surface Area of Can
= 2πrh
= 2 x 3.14 x 3.5 x 10
= 219 cm²
Learn more about Surface area here:
https://brainly.com/question/2835293
#SPJ1
help fast please
i have no idea what to do in math so i need help

Answers
Answer:
see the attachment photo!

The functions f(x) = −(x − 1^)2 + 5 and g(x) = (x + 2)^2 − 3 have been rewritten using the completing-the-square method. Apply your knowledge of functions in vertex form to determine if the vertex for each function is a minimum or a maximum and explain your reasoning.
Answers
If we write a quadratic in vertex form:
\(y=a(x-h)^2+k\)
Then:
\(\bold{a}\) \(\longrightarrow\) is the coefficient of \(x^2\)
\(\bold{h}\) \(\longrightarrow\) is the axis of symmetry.
\(\bold{k}\) \(\longrightarrow\) is the max/min value of the function.
Also:
If \(a > 0\) then the parabola will be of the form \(\cup\) and will have a minimum value.
\(a < 0\) then the parabola will be of the form \(\cap\) and will have a minimum value.
For the given functions:
\(a < 0\)
\(f(x)=-(x-1)^2+5\) this has a maximum value of \(\bold{5}\)
\(a > 0\)
\(f(x)=(x+2)^2-3\) this has a minimum value of \(\bold{-3}\)
Which of the following statements about points are false?
Check all that apply.
A. Their sizes vary.
B. They have no size and no dimensions,
C. They have no length or height.
D. Their size depends on their dimensions.
Answers
Answer:
their sizes vary
Step-by-step explanation:
their sizes vary
Determine if the expression is decreased n by 8% or increased n by 8%.

Answers
To determine if each expression is decreased or increased by 8% you can substitute the n in the expressions by 100 and then evaluate the expression, if the result is 92 it decrease, if it is 108 it increase:
First expression: decrease n by 8%
\(\begin{gathered} 0.92n \\ 0.92(100)=92 \end{gathered}\)Second expression: increase n by 8%
\(\begin{gathered} 1.08n \\ 1.08(100)=108 \end{gathered}\)Third expression: increase n by 8%
\(\begin{gathered} n+0.08n \\ 100+0.08n=108 \end{gathered}\)Fourth expression: decreased n by 8%
\(\begin{gathered} n-0.08n \\ 100-0.08(100)=92 \end{gathered}\)Which algebraic expression is equivalent to the expression below?
14x + 4- 6x
A. 4(x + 1)
B. 4(2x + 1)
C. 4(2x - 1)
D..8(x + 1)
Answers
Answer:
4(2x + 1)
Step-by-step explanation:
14x + 4 - 6x
Rearrange the expression with like terms together
14x - 6x + 4
8x + 4
Factorize the expression
4(2x + 1)
Solve the following pair of simultaneous equations by drawing a graph.
y – 2x = 1 and 2y – x = 8
Answers
Answer:
\(x = 2\)
\(y = 5\)
Step-by-step explanation:
The graph is in the attached image above

Answer:
(2, 5)=======================
Given equations:
y - 2x = 1 and2y - x = 8Solve by graphing, graph each line and find the point the lines intersect, this point is the solution.
See the attached, the solution is (2, 5)

The product of two numbers is 1536.
If the HCF of the two numbers is 16.
find the LCM of these two numbers.
Answers
Work Shown:
LCM = (product of two numbers)/(HCF of the two numbers)
LCM = 1536/16
LCM = 96
In a certain video game, there is a mini-game where the main character can choose from a selection of twenty
presents. The presents are wrapped, so the character does not know what is in them. If 7 presents contain money, 3
presents contain gems, 6 presents contain ore, and 4 presents contain fish, what is the probability that the main
character does not choose a present that contains a gem?
Your answer should be an exact decimal value.
The probability of randomly selecting a present that does not contain a gem is
Answers
Answer:
There are a total of 20 presents, and 3 of them contain gems. Therefore, there are 20 - 3 = 17 presents that do not contain gems.
The probability of randomly selecting a present that does not contain a gem is 17/20 = 0.85 or 85%.
hope it helps you...
Abby is filling a 100 quart dog bath using a 2 gallon bucket. how many buckets will it take to fill the dog bath?
Answers
( or 12.5 buckets)
Step by step
We know the bath holds 100 quarts
We know 100 quarts is equal to 25 gallons
( 4qts to 1 gallon)
If Abby is using a 2 gallon bucket, divide 25 gallons by 2
25/2 = 12 1/2 buckets to fill the bath
Suppose that before you began your college application process, you were offered a job to work as a floor-trainer at a local yoga studio, accompanied by a yearly salary of $27,000 (after taxes). Assume however that you decided to turn down this offer and instead attend a year of college. The total monetary cost of the year of college, including tuition, fees, and room and board expenses, is $43,000.
1. Understanding opportunity cost Suppose that before you began your colle by a yearly salary of
$27,000
(after taxes) monetary cost of the year of college, inclu
Answers
The value of a year of college is more than $70000
The person decided to turn down this offer and instead attend a year of college
The total monetary cost of the year of college, including tuition, fees, and room and board expenses, is $43,000.
This means that the person has forgone the salary from working as a floor trainer. This is the opportunity cost of attending the college
Opportunity cost = $27000
Cost of attending college = $43000
Total cost = $27000+ $43000= $70000
Despite a cost of $70000 the person decides to attend the college showing that he values the college More than the salary that he would have earned from working
So he values the college more than $70000
Learn more about Opportunity cost at:
https://brainly.com/question/13036997
#SPJ4
What is the answer?
2/5 + 3/4
Answers
Take LCM
5×4=20Now
2/5+3/48+15/2023/20Answer:
23/20
Step-by-step explanation:
2/5 + 3/4
LCM = 5 * 4 = 20
=》2/5 * 4/4 = 8/20
=》3/4 * 5/5 = 15/20
So,
2/5 + 3/4
= 8/20 + 15/20
= 23/20
_________
Hope it helps ⚜
Find the area of the irregular figure
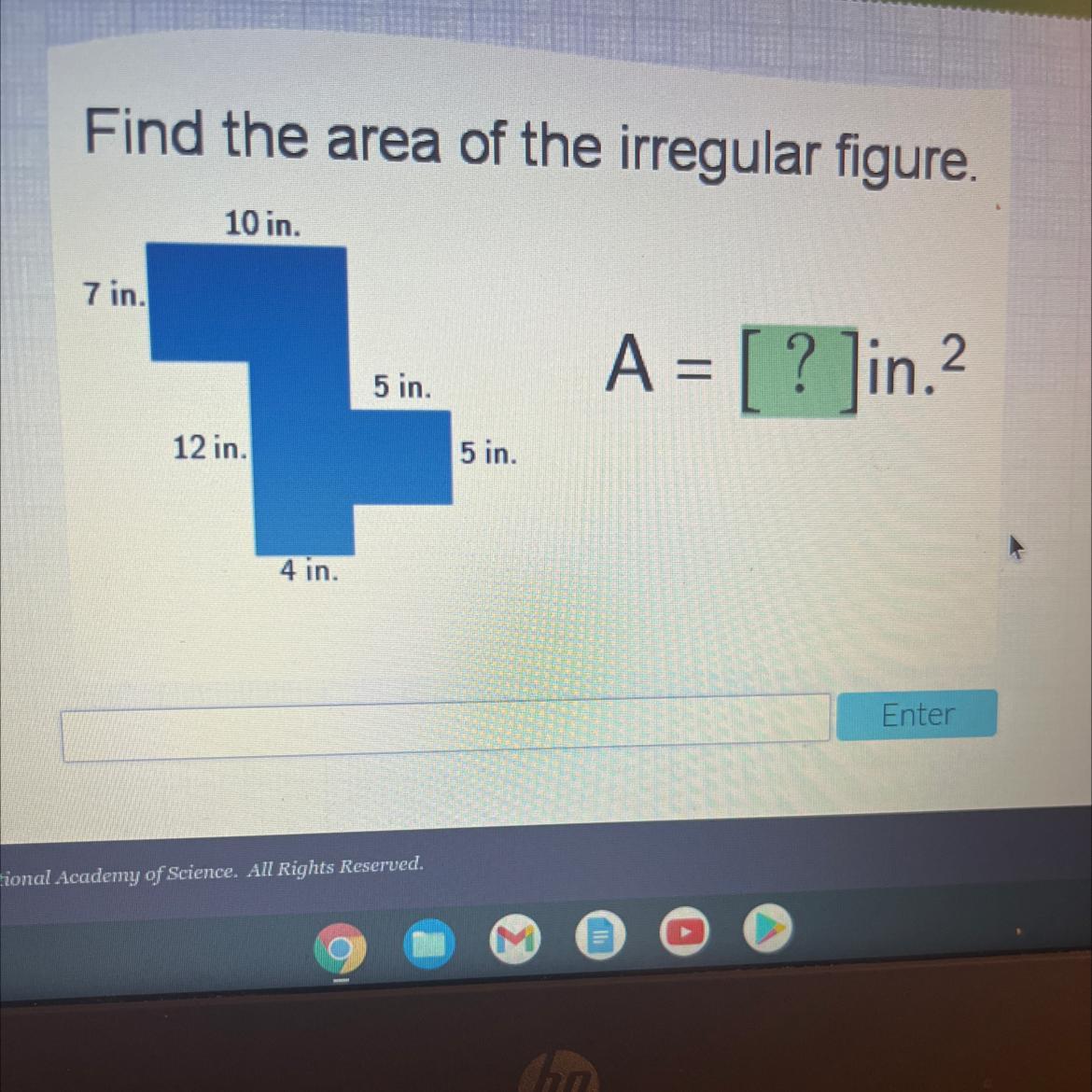
Answers
Answer:
143 in.²
Step-by-step explanation:
area = l × b = 7 × 10 = 70 in.²
12 × 4 = 48 in.²
5 × 5 or 5² = 25 in.²
now,
add them
70 + 48 + 25 = 143 in.²
therefore, area of the given figure is 143 in.².
hope this helps you !
help please im so lost


Answers
Volume of given two cylinders are 115.52π m³ and 350π in³
What is the formula for the volume of a cylinder?
\(V = π {r}^{2} h\)
where r is the radius of the cylinder, h is the height of the cylinder, and π is a constant approximately equal to 3.14.
4) Given, radius =3.8 m and height = 8 m
Substituting the given values into the formula, we get:
\(V = π × (3.8)^2 × 8 \\ V = 115.52\pi \: cubic \: meters\)
Therefore, the volume of the cylinder is approximately 361.984 cubic meters.
5) Given, radius = 5 in and height = 14 in
Substituting the given values:
\(V = π(5²)(14) \\ V = π(25)(14) \\ V = 350π\)
Therefore, the volume of the cylinder is 350π cubic in (or approximately 1099.56 cubic meters if you want to use a numerical approximation for π).
Volume related one more question:
https://brainly.com/question/463363
#SPJ1