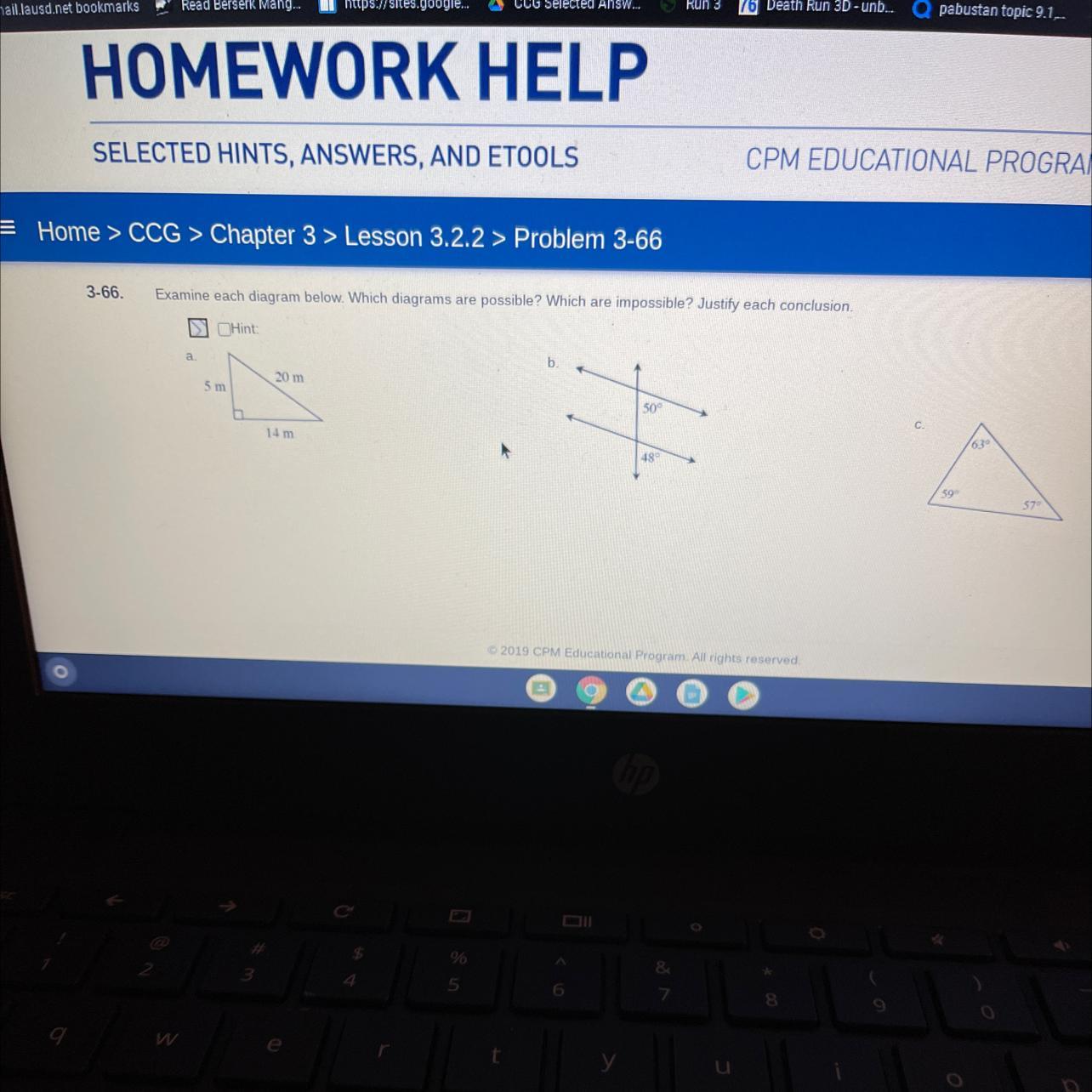
Problem 3-66
Examine each diagram below. Which diagrams are possible? Which are impossible? Justify each conclusion
Hint:
Answers
Answer:
All of them is impossible in mathematics
Step-by-step explanation:
In the first diagram we see a right triangle, which we can use pythagorean theorem to verify , but 20^2-14^2 does not equal to 5^2
IN the second diagram, According to the corresponding angles theorem, the statement “If a line intersects two parallel lines, then the corresponding angles in the two intersection regions are congruent” is true either way. But in the diagram we see 50 isn't equal to 48, hence it's a false statement too.
In the third diagram, we see we can verify it using the summation of triangle a+b+c=180, we clearly see 63+59+57 isn't equal to 180
So, indeed, all of the three diagram is impossible to exist in mathematics
Related Questions
Solve the given equation by completing the square.
Fill in the values of a, b, and e to complete the solutions.

Answers
The solution in this case is x = (4 + sqrt(102+4c))/2 - 4√c, which can be expressed in the form of X = a - b√c.
How to solve quadratic equation?
To solve the equation x²+8x-38=0, we can use the quadratic formula:
x = (-b ± sqrt(b²-4ac)) / 2a
Here, a=1, b=8, and c=-38. Substituting these values into the formula gives:
x = (-8 ± sqrt(8²-4(1)(-38))) / 2(1)
x = (-8 ± sqrt(324)) / 2
x = (-8 ± 18) / 2
So x is either -13 or 5.
To find the values of x in the form of X = a + b√c and X = a - b√c, we can use the following steps:
For X=a+b√c:
Let's assume that x = a + b√c, where a, b, and c are constants to be determined.
Substituting this into the original equation x²+8x-38=0, we get:
(a + b√c)² + 8(a + b√c) - 38 = 0
Expanding the square and simplifying, we get:
(a² + 2ab√c + b²c) + 8a + 8b√c - 38 = 0
Separating the real and imaginary parts, we get:
(a² + b²c + 8a - 38) + (2ab√c + 8b)√c = 0
Since the real and imaginary parts of the equation must both be zero, we can set them each equal to zero and solve for a, b, and c.
First, setting the real part equal to zero gives:
a² + b²c + 8a - 38 = 0
This is a quadratic equation in a, so we can use the quadratic formula:
a = (-8 ± sqrt(8²-4(bc-38))) / 2
Simplifying this gives:
a = -4 ± sqrt(4+b(b-10))
Now, setting the imaginary part equal to zero gives:
2ab + 8b = 0
Solving for b, we get:
b = 0 or b = -4
If b = 0, then a² + b²c + 8a - 38 = a² + 8a - 38 = 0, which has roots a = -5 and a = 3. Therefore, the solution in this case is x = -5 or x = 3, which cannot be expressed in the form of X = a + b√c.
If b = -4, then a² + b²c + 8a - 38 = a² + 16c + 8a - 38 = 0. Plugging this into the quadratic formula for a, we get:
a = -4 ± sqrt(102-4c)/2
Therefore, the solution in this case is x = (-4 + sqrt(102-4c))/2 - 4√c, which can be expressed in the form of X = a + b√c.
For X=a-b√c:
Using the same logic, we can assume that x = a - b√c, where a, b, and c are constants to be determined.
Substituting this into the original equation x²+8x-38=0, we get:
(a - b√c)² + 8(a - b√c) - 38 = 0
Expanding the square and simplifying, we get:
(a² + b²c - 8a - 38) + (-2ab√c - 8b)√c = 0
Since the real and imaginary parts of the equation must both be zero, we can set them each equal to zero and solve for a, b, and c.
Setting the real part equal to zero gives:
a² + b²c - 8a - 38 = 0
This is a quadratic equation in a, so we can use the quadratic formula:
a = (8 ± sqrt(8²+4(bc+38))) / 2
Simplifying this gives:
a = 4 ± sqrt(4+b(b+10))
Setting the imaginary part equal to zero gives:
-2ab - 8b = 0
Solving for b, we get:
b = 0 or b = -4
If b = 0, then a² + b²c - 8a - 38 = a² - 8a - 38 = 0, which has roots a = -3 and a = 11. Therefore, the solution in this case is x = -3 or x = 11, which cannot be expressed in the form of X = a - b√c.
If b = -4, then a² + b²c - 8a - 38 = a² + 16c - 8a - 38 = 0. Plugging this into the quadratic formula for a, we get:
a = 4 ± sqrt(102+4c)/2
Therefore, the solution in this case is x = (4 + sqrt(102+4c))/2 - 4√c, which can be expressed in the form of X = a - b√c.
To know more about Equation visit :-
https://brainly.com/question/22688504
#SPJ1
Explain why the probability of rolling a sum from 2 to 12 is 100%. [C:2]
Answers
The probability of rolling a sum from 2 to 12 on 2 dices is 100%
Given the data,
The two dice should be rolled.
Now, there are 36 possibilities that might occur while rolling two normal six-sided dice. The reason for this is that when rolling two dice, the total number of outcomes is the product of the numbers of outcomes for each die, and each die has six potential outcomes (numbers 1 through 6).
The resultant 36 results are as follows:
1-1, 1-2, 1-3, 1-4, 1-5, 1-6
2-1, 2-2, 2-3, 2-4, 2-5, 2-6
3-1, 3-2, 3-3, 3-4, 3-5, 3-6
4-1, 4-2, 4-3, 4-4, 4-5, 4-6
5-1, 5-2, 5-3, 5-4, 5-5, 5-6
6-1, 6-2, 6-3, 6-4, 6-5, 6-6
When using two dice, there are a total of 36 possibilities that might occur.
As a result, the results' total ranges from 2 to 12.
Hence , the probability is 100 %
Click here for additional information about probability.
https://brainly.com/question/17089724
#SPJ1
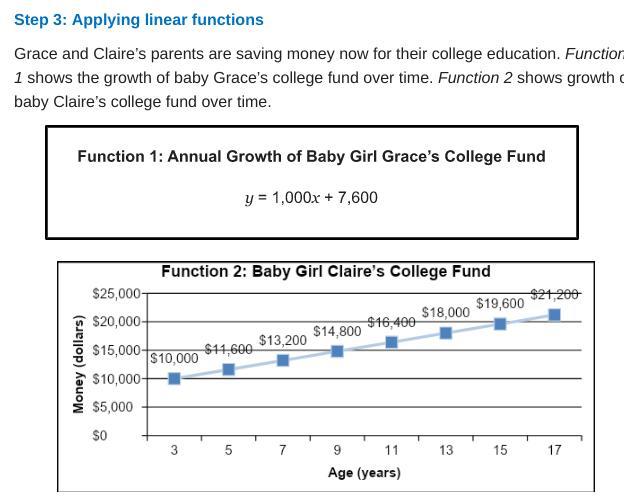
a) If Grace and Claire’s parents each invested $7,600 into a college saving account when the girls were born, how much money will each girl have for college when she turns 18? Explain. (2 points)
b) Do the functions show a positive or negative correlation between time and the amount of money saved? Explain. (1 point)
Answers
Grace would have an amount of $25,600 at the end of 18 years old and Claire would have $22,000 when she turns 18 years old.
There is a positive correlation
How to find the correlation of function?The function that represents the annual growth of baby girl grace's college fund is given by; y = 1000x + 7600
For Grace, plug in 18 for x to get;
y = 1000(18) + 7600
y = 18000 + 7600
y = 25600
For Claire, let us first find the slope;
Slope = 11600 - 10000/3
Slope = 800
Therefore, the function for Claire is expressed as;
y= 800x + 7600
For Claire, plug in 18 for x to get;
y = 800(18) + 7600
y = 14,400 + 7600
y = 22,000
Therefore, Grace would have an amount of $25,600 at the end of 18 years old and Claire would have $22,000 when she turns 18 years old.
Read more about Function Correlation at; https://brainly.com/question/28091015
#SPJ1
Consider this system of equations. y=2x x+2y=15
Answers
Answer:
x=3
y=6
Step-by-step explanation:
ez pz
Jane has been practicing sewing, and she wants to make a rectangular blanket to give as a gift to her best friend. So that the blanket is not too small, Jane decides the blanket will have an area of approximately 40 square feet, or 5,760 square inches. She also wants the blanket to be 18 inches longer than it is wide to have room to embroider her friend's name along one edge.
To the nearest tenth of an inch, what is the width of the blanket?
Answers
The width of the blanket to the nearest tenth of an inch is approximately 67.4 inches.
What is width in rectangle ?
In a rectangle, the width refers to the measurement of the shorter side of the rectangle, which is perpendicular to its length.
Let x be the width of the blanket in inches. Then the length of the blanket is x + 18 inches.
The area of the blanket is given by:
Area = Length x Width
5760 sq inches = (x + 18) inches * x inches
Expanding the right-hand side and solving for x, we get:
\(x^2 + 18x - 5760 = 0\)
We can solve this quadratic equation using the quadratic formula:
\(x = (-b \pm \sqrt{(b^2 - 4ac)}) / 2a\)
where a = 1, b = 18, and c = -5760. Plugging in these values, we get:
\(x = (-18 \pm \sqrt{(18^2 - 4(1)(-5760))}) / 2(1)\)
\(x = (-18 \pm \sqrt{(18^2 + 23040)}) / 2\)
x ≈ 67.42 or x ≈ -85.42
Since the width cannot be negative, the width of the blanket to the nearest tenth of an inch is approximately 67.4 inches.
To learn more about quadratic equation from the given link :
https://brainly.com/question/30098550
#SPJ1
Directions - Find the sector areas of both the grey and white areas:
*Use 3.14 in place of
285⁰
8 in
in²
in
(round to two decimal places)
(round to two decimal places)
E
Answers
The sector areas of the grey and white areas are 159.09 in² and 41.87 in²
Finding the sector areas of the grey and white areas:From the question, we have the following parameters that can be used in our computation:
Radius, r = 8 inchesCentral angle,= 45 degreesThe area of shaded sector is calculated as
Area = Central angle/360 * π * Radius^2
Substitute the known values in the above equation, so, we have the following representation
Gray = 285/360 * 3.14 * 8^2 = 159.09White = (360 -285)/360 * 3.14 * 8^2 = 41.87Hence, the area is 159.09
Read mroe about area at
brainly.com/question/16656203
#SPJ1
4. Solve the system of equations without graphing. *2v + 6w = -365v + 2w = 1
Answers
Given the equation system:
\(\begin{gathered} 2v+6w=-36 \\ 5v+2w=1 \end{gathered}\)To solve the equation system, you can use the substitution method.
First, write one of the equations for one of the variables, for example, write the second equation for v:
\(5v+2w=1\)Pass 2w to the right side of the equation by applying the opposite operation to both sides of it:
\(\begin{gathered} 5v+2w-2w=1-2w \\ 5v=1-2w \end{gathered}\)Divide both sides by 5
\(\begin{gathered} \frac{5v}{5}=\frac{1}{5}-\frac{2}{5}w \\ v=\frac{1}{5}-\frac{2}{5}w \end{gathered}\)Second, replace the expression obtained into the first equation:
\(\begin{gathered} 2v+6w=-36 \\ 2(\frac{1}{5}-\frac{2}{5}w)+6w=-36 \end{gathered}\)Now you have to solve the expression for w:
Distribute the multiplication on the parentheses term:
\(\begin{gathered} 2\cdot\frac{1}{5}-2\cdot\frac{2}{5}w+6w=-36 \\ \frac{2}{5}-\frac{4}{5}w+6w=-36 \\ \frac{2}{5}+\frac{26}{5}w=-36 \end{gathered}\)Subtract 2/5 to both sides of the equal sign:
\(\begin{gathered} \frac{2}{5}-\frac{2}{5}+\frac{26}{5}w=-36-\frac{2}{5} \\ \frac{26}{5}w=-\frac{182}{5} \end{gathered}\)Multiply both sides by the reciprocal of 26/5
\(\begin{gathered} (\frac{26}{5}\cdot\frac{5}{26})w=(-\frac{182}{5})(\frac{5}{26}) \\ w=-7 \end{gathered}\)Once you determine the value of w, you can calculate the value of v
\(\begin{gathered} v=\frac{1}{5}-\frac{2}{5}w \\ v=\frac{1}{5}-\frac{2}{5}(-7) \\ v=\frac{1}{5}+\frac{14}{5} \\ v=\frac{15}{5}=3 \end{gathered}\)The solution of the equation system is w=-7 and v=3
Solve the equation for the indicated variable. C=680x/h^2 for x

Answers
Answer:
C h^2 / 680 = x
Step-by-step explanation:
C=680x/h^2
Multiply each side by h^2
C h^2=680x/h^2 * h^2
C h^2=680x
Divide each side by 680
C h^2 / 680=680x/680
C h^2 / 680 = x
That gives you Ch^2= 680x
Second step: divide both sides by 680
That gives you (ch^2)/680=x
Simplify: x= (ch^2)/680
That is the simplest form
Please help I’ll mark you as brainliest if correct!!!

Answers
Part B) the next three numbers are 26,31,and 36. this is an arithmetic sequence because you simply add 5 to each number previously.
Classify this event: Draw a card from a deck of cards, then draw a second card.
O a dependent
b. outcome
O c complementary
O d. independent
Answers
Add 238 and 12, then multiply by 3. Interpret the expression.
Answers
Answer:
3(238+12) is the expression
Step-by-step explanation:
hope this helps
the way i interpreted this expression is 3(238+12)
5. On a cattle farm, the ratio of beef cattle to dairy cattle is 4:3.
3
(a) Interpret the ratio: For every
beef cattle, there are
cattle.
dairy
(b) If there are 24 dairy cattle, how many
beef cattle would there be? Show your
work.
Answers
For every 4 beef cattle there is 3 dairy cattle. For 24 dairy cattle there will be 32 beef cattle as per the given ratio of 3:4.
What is ratio?An ordered pair of numbers a and b, written as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value. For instance, you could write the ratio as follows: 1: 3 if there is 1 boy and 3 girls (for every one boy there are 3 girls). The ratio can be defined as the number that can be used to represent one quantity as a percentage of another. Only when the two numbers in a ratio have the same unit can they be compared. Ratios are used to compare two things.
Here,
a. No for every 4 beef cattle there is 3 dairy cattle.
b. 4/3=x/24
x=4*24/3
x=32 beef cattle
There are 3 dairy cattle for every 4 beef cattle. According to the stated ratio of 3:4, there will be 32 beef cattle for every 24 dairy cattle.
To know more about ratio,
https://brainly.com/question/13419413?referrer=searchResults
#SPJ13
NO LINKS!!! URGENT HELP PLEASE!!!
State if the given functions are inverses.
1. g(x) = 4 + (7/2)x
f(x) = 5 - (4/5)x
Find the inverses of each function.
2. g(n) = (8/3)n + 7/3
3. g(x) = 1 - 2x^3
Answers
Answer:
1) The functions are not inverses.
\(\textsf{2)} \quad g^{-1}(n)=&\dfrac{3}{8}n-\dfrac{7}{8}\)
\(\textsf{3)} \quad g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\)
Step-by-step explanation:
Question 1The inverse composition rule states that if two functions are inverses of each other, then their compositions result in the identity function.
Given functions:
\(g(x) = 4 + \dfrac{7}{2}x \qquad \qquad f(x) = 5 - \dfrac{4}{5}x\)
Find g(f(x)) and f(g(x)):
\(\begin{aligned} g(f(x))&=4+\dfrac{7}{2}f(x)\\\\&=4+\dfrac{7}{2}\left(5 - \dfrac{4}{5}x\right)\\\\&=4+\dfrac{35}{2}-\dfrac{14}{5}x\\\\&=\dfrac{43}{2}-\dfrac{14}{5}x\\\\\end{aligned}\) \(\begin{aligned} f(g(x))&=5 - \dfrac{4}{5}g(x)\\\\&=5 - \dfrac{4}{5}\left(4 + \dfrac{7}{2}x \right)\\\\&=5-\dfrac{16}{5}-\dfrac{14}{5}x\\\\&=\dfrac{9}{5}-\dfrac{14}{5}x\end{aligned}\)
As g(f(x)) or f(g(x)) is not equal to x, then f and g cannot be inverses.
\(\hrulefill\)
Question 2To find the inverse of a function, swap the dependent and independent variables, and solve for the new dependent variable.
Calculate the inverse of g(n):
\(\begin{aligned}y &= \dfrac{8}{3}n + \dfrac{7}{3}\\\\n &= \dfrac{8}{3}y + \dfrac{7}{3}\\\\3n &= 8y + 7\\\\3n-7 &= 8y\\\\y&=\dfrac{3}{8}n-\dfrac{7}{8}\\\\g^{-1}(n)&=\dfrac{3}{8}n-\dfrac{7}{8}\end{aligned}\)
Calculate the inverse of g(x):
\(\begin{aligned}y &= 1-2x^3\\\\x &= 1-2y^3\\\\x -1&=-2y^3\\\\2y^3&=1-x\\\\y^3&=\dfrac{1}{2}-\dfrac{1}{2}x\\\\y&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\\end{aligned}\)
Answer:
1.
If the composition of two functions is the identity function, then the two functions are inverses. In other words, if f(g(x)) = x and g(f(x)) = x, then f and g are inverses.
For\(\bold{g(x) = 4 + \frac{7}{2}x\: and \:f(x) = 5 -\frac{4}{5}x}\), we have:
\(f(g(x)) = 5 - \frac{4}{5}(4 + \frac{7}{2}x)\\ =5 - \frac{4}{5}(\frac{8+7x}{2})\\=5 - \frac{2}{5}(8+7x)\\=\frac{25-16-14x}{5}\\=\frac{9-14x}{5}\)
\(g(f(x)) = 4 + (\frac{7}{5})(5 - \frac{4}{5}x) \\=4 + (\frac{7}{5})(\frac{25-4x}{5})\\=4+ \frac{175-28x}{25}\\=\frac{100+175-28x}{25}\\=\frac{175-28x}{25}\)
As you can see, f(g(x)) does not equal x, and g(f(x)) does not equal x. Therefore, g(x) and f(x) are not inverses.
Sure, here are the inverses of the functions you provided:
2. g(n) = (8/3)n + 7/3
we can swap the roles of x and y and solve for y to find the inverse of g(n). In other words, we can write the equation as y = (8/3)n + 7/3 and solve for n.
y = (8/3)n + 7/3
n =3/8*( y-7/3)
Therefore, the inverse of g(n) is:
\(g^{-1}(n) = \frac{3}{8}(n - \frac{7}{3})=\frac{3}{8}*\frac{3n-7}{3}=\boxed{\frac{3n-7}{8}}\)
3. g(x) = 1 - 2x^3
We can use the method of substitution to find the inverse of g(x). We can substitute y for g(x) and solve for x.
\(y = 1 - 2x^3\\2x^3 = 1 - y\\x = \sqrt[3]{\frac{1 - y}{2}}\)
Therefore, the inverse of g(x) is:
\(g^{-1}(x) =\boxed{ \sqrt[3]{\frac{1 - x}{2}}}\)
Mike Danes has been delayed in going to the annual sales event at one of his favorite apparel stores. His friend has just texted him that there are only 20 shirts left, of which 8 are in size M, 10 in size L, and 2 in size XL. Also 9 of the shirts are white, 5 are blue, and the remaining are of mixed colors. Mike is interested in getting a white or a blue shirt in size L. Define the events A = Getting a white or a blue shirt and B = Getting a shirt in size L. a. Find P(A), P(A^c), and P(B). b. Are the events A and B mutually exclusive? Explain. c. Would you describe Mike's preference by the events A u B or A n B?
Answers
a) Probability of occurrence of evant A is equals to the 7/10.
P(not getting a white or a blue shirt), P(Aᶜ ) is equals the 3/10.
Probability of occurrence of evant B is equal to the 1/2.
b) The events A and B are not mutually exclusive
c) Mike's preference is to getting a white shirt with his size L.
We have a probabality based problem. Probability is defined as chance of occurrence of an event or result. It can be calculate as favourable outcomes divided by total possible outcomes. There is total number of avaliabile shirts = 20 i.e., total possible outcomes = 20
Mike is interested in getting a white or a blue shirt in size L. Let us consider two events :
A : Getting a white or a blue shirt
B: Getting a shirt in size L
a) Number of favourable outcomes to getting white or a blue shirt = 9 white or 5 blues
Probability ( Getting a white or a blue shirt) , P(A)
= 9/20 + 5/20 + 0 = 14/20 = 7/10
P(not Getting a white or a blue shirt), P(Aᶜ )
= 1 - P(A) = 1 - 7/10 = 3/10
ii) The number of favourable outcomes for event B, n(B) = 10
So, Probability of getting a shirt in size L, P(B)
= 10/20 = 1/2
b) Mutually exclusive events are defined as the events that can't happen at the same time. In other words AnB = 0 . Here, we see there is total 14 shirts which are in white or blue colors and 10 are in size L , So there is possibility that shirt is white or blue in colour and in size L , i.e, An B ≠0
So, events A and B are not mutually exclusive.
c) Event ,n( A u B )= n(A) + n(B) - n(A n B)
On the basis of all details, we conclude that Mike's preference is to choose white shirt with size L .
To learn more about Probability, refer:
https://brainly.com/question/25870256
#SPJ4
What is the factored form of the polynomial? x + 9x +20 O (x - 4)(x - 5) O (x - 2)(x - 10) 〇(x+4)(x + 5) O (x + 2)(x + 10)
Answers
The factored form of the polynomial x + 9x + 20 is (x + 4)(x + 5). To obtain this form, we can use the factoring method known as "FOIL," which stands for "First, Outer, Inner, Last." This method involves multiplying the first terms, the outer terms, the inner terms, and the last terms of the two factors to obtain the original polynomial.
In this case, if we let the factors be (x + 4) and (x + 5), we can use FOIL to multiply them and obtain the following:
(x + 4)(x + 5) = (x * x) + (4 * x) + (x * 5) + (4 * 5)
This simplifies to:
(x + 4)(x + 5) = x^2 + 9x + 20
As we can see, the result is the original polynomial. Therefore, the factored form of x + 9x + 20 is (x + 4)(x + 5)
The value of the factored form of the polynomial are,
⇒ (x + 4) (x + 5)
What is Quadratic equation?An algebraic equation with the second degree of the variable is called an Quadratic equation.
Given that;
The polynomial are,
⇒ x² + 9x + 20
Now, We can simplify as;
⇒ x² + 9x + 20
⇒ x² + 5x + 4x + 20
⇒ x (x + 5) + 4 (x + 5)
⇒ (x + 4) (x + 5)
Thus, The value of the factored form of the polynomial are,
⇒ (x + 4) (x + 5)
Learn more about the quadratic equation visit:
brainly.com/question/1214333
#SPJ5
x/3 =-8 x=? what does x =?
Answers
Answer: -24
Step-by-step explanation:
\(\frac{x}{3}=-8\\\frac{x}{3}(3)=-8(3)\\ x=-24\)
if you actually know plz give an explanation to the answer so i know you aren't just answering for points, please help this is due before 12:00

Answers
Answer:
A.
Step-by-step explanation:
it is the only one that makes sense, because it deals with 8th graders, all others include gender which i do not think that matters.
angle 0 is in quadrant I with cos 0 is 10/17. which of the following would be the appropriate step in calculating the value of sin 0 using the pythagorean identity?
a. sin 0 + (10/17)^2 = 1
b. sin 0 - (10/17)^2 = 1
c. sin^2 0 + (10/17)^2 = 1
d. sin^2 0 - (10/17)^2 = 1
Answers
Work Shown:
\(\sin^2(\theta) + \cos^2(\theta) = 1\\\\\sin^2(\theta) + \left(\cos(\theta)\right)^2 = 1\\\\\sin^2(\theta) + \left(\frac{10}{17}\right)^2 = 1\)
As the name implies, the pythagorean identity uses the pythagorean theorem for right triangles. The 1 on the right hand side is the length of the hypotenuse, which is the radius of the unit circle.
what multiplies to -65 and adds to -8
Answers
Answer: The two numbers that multiply to -65 and add to -8 are -13 and 5.
Steps: Here are the steps to find two numbers that multiply to -65 and add to -8:
Write down the equation x * y = -65 where x and y are the two numbers you’re looking for.
Write down the equation x + y = -8.
Solve for one of the variables in one of the equations. For example, solving for x in the second equation gives us x = -8 - y.
Substitute this expression for x into the first equation: (-8 - y) * y = -65.
Solve this quadratic equation for y: -y^2 - 8y + 65 = 0.
Use the quadratic formula to find the values of y: y = (-(-8) +/- sqrt((-8)^2 - 4 * (-1) * 65)) / (2 * (-1)).
This gives us two possible values for y: -13 and 5.
Substitute these values back into one of the original equations to find the corresponding values of x. For example, when y = -13, we have x = -8 - (-13) = 5. When y = 5, we have x = -8 - 5 = -13.
So, the two numbers that multiply to -65 and add to -8 are -13 and 5.
How would you set up f(3) that’s supposed to xsquared
F(X)=7x2-2x
Answers
The solution for f(3) in the function f(x) = 7x² - 2x is 57
How to determine the solution for A(3) in the function?From the question, we have the following equation that can be used in our computation:
F(X) = 7x2-2x
To make the equation legible, we need to rewrite it
So, we have the following representation
f(x) = 7x² - 2x
Also from the question, we have
f(3)
This means that the value of x is 3, and we calculate f(x) when x = 3
Substitute the known values in the above equation, so, we have the following representation
f(3) = 7x² - 2x
So, we have the following equation
f(3) = 7(3)² - 2(3)
There are constants to add or subtract to both sides of the equation
So, we have the following representation
f(3) = 57
Hence, the solution is 57
Read more about functions at
brainly.com/question/28277110
#SPJ1
16. What is the volume of the composite figure? 8 ft 4 ft 6 ft 3 ft 2 ft
Answers 96 ft³3 76 ft³ 152 ft³ 192 ft³
Answers
The volume of the composite figure is 228 ft³.
To calculate the volume of a composite figure, we need to break it down into its individual components and then sum up the volumes of each component.
From the given dimensions, it seems that the composite figure consists of multiple rectangular prisms. Let's calculate the volume of each prism and then add them together.
First prism:
Length = 8 ft, Width = 4 ft, Height = 6 ft
Volume = Length * Width * Height = 8 ft * 4 ft * 6 ft = 192 ft³
Second prism:
Length = 3 ft, Width = 2 ft, Height = 6 ft
Volume = Length * Width * Height = 3 ft * 2 ft * 6 ft = 36 ft³
Now, let's add the volumes of both prisms:
192 ft³ + 36 ft³ = 228 ft³
Therefore, the volume of the composite figure is 228 ft³.
for similar questions on volume.
https://brainly.com/question/463363
#SPJ8
What is the volume of the composite figure? 8 ft 4 ft 6 ft 3 ft 2 ft
Answers 96 ft³3 76 ft³ 228 ft³ 192 ft³
Simplify this algebraic expression.

Answers
4/4 = 1
z-1+8 = z+7
C. z+7
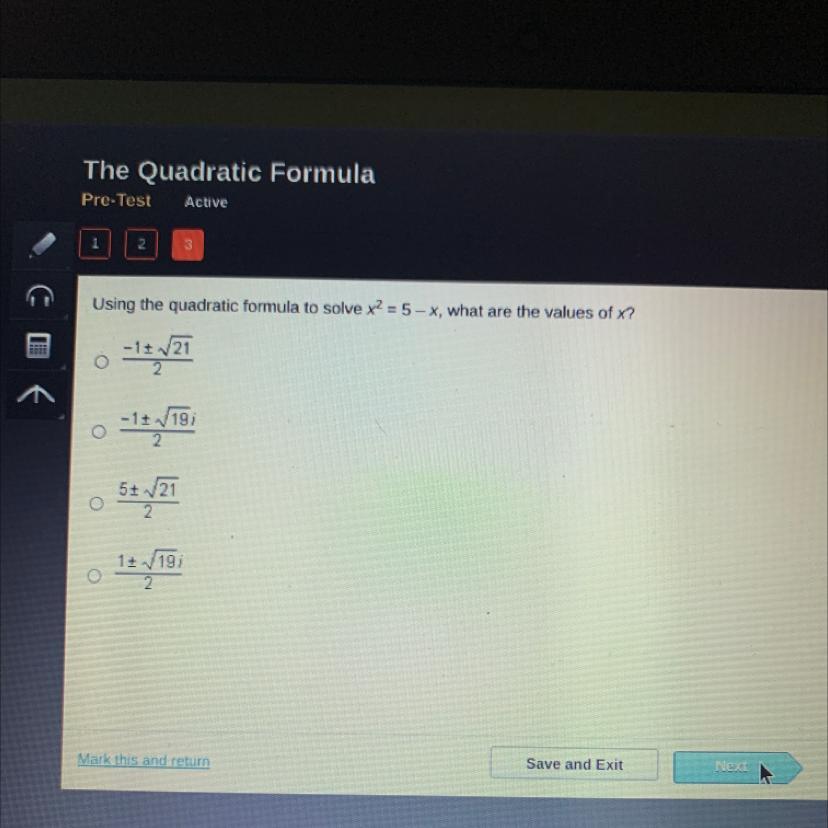
Using the quadratic formula to solve x2 35-x, what are the values of x?
-12-121
-12-11
54.
12/19
51 21
2
Answers
Answer:
x = (-1 ± √21) / 2
The first choice
Step-by-step explanation:
x² = 5 - x
Put in standard form
x² + x - 5 = 0
Use quadratic equation
x = ( -b ± √( b² - 4ac) ) / (2a)
Plug in a = 1, b = 1 , c = -5
x = (-1 ± √( 1² - 4*1*(-5)) ) / 2
evaluate
x = (-1 ± √21) / 2
THERE ARE 2 PARTS PLEASE ANSWER BOTH RIGHT TY HELPP!! There are 12 red cards, 17 blue cards, 14 purple cards, and 7 yellow cards in a hat.
Part A. What is the THEORETICAL probability of drawing a purple card from the hat?
Part B.
In a trial, a card is drawn from the hat and then replaced 1,080 times. A purple card is drawn 324 times. How much greater is the experimental probability than the theoretical probability?
Enter the correct answers in the boxes.
A. The theoretical probability of drawing a purple card from the hat is ______.
B. The experimental probability of drawing a purple card is ____%
greater than the theoretical probability.
Answers
Answer: Below :)
Step-by-step explanation:
Part A:
The theoretical probability of drawing a purple card from the hat is the number of purple cards divided by the total number of cards in the hat:
P(purple) = 14 / (12 + 17 + 14 + 7) = 14 / 50 = 0.28
So the theoretical probability of drawing a purple card is 0.28 or 28%.
Part B:
The theoretical probability of drawing a purple card is 0.28.
The experimental probability of drawing a purple card is the number of times a purple card was drawn divided by the total number of draws:
Experimental probability = 324 / 1080 = 0.3
To find how much greater the experimental probability is than the theoretical probability, we can calculate the difference and express it as a percentage:
Difference = Experimental probability - Theoretical probability
Difference = 0.3 - 0.28 = 0.02
Percentage greater = (Difference / Theoretical probability) x 100%
Percentage greater = (0.02 / 0.28) x 100% = 7.14%
So the experimental probability is 7.14% greater than the theoretical probability.
Melody picks a number. She triples the number, squares the result, divides the square by 2, subtracts 30 from the quotient, and gets 42. What are the possible numbers that Melody could have picked?
Answers
The possible numbers that Melody could have picked are -4 and 4.
The operation that prevents us from knowing with 100% certainty the number Melody had picked is multiplication which is implied by the phrase "double the number".
Given, Let x be the number Melody had chosen.
Thus, tripling the number will give 3x, and
squaring this will result to (3x)² which is equals to 9x².
Dividing the square of the number by 2 and subtracting 30 from its quotient will give 42:
9x²/2 ₋ 30 = 42
9x²/2 = 42 ₊ 30
9x²/2 = 72
9x² = 72 × 2
9x² = 144
x² = 144/9
x² = 16
x = ±√16
x = ±4
x = ₊4 or x = 4
hence melody could have picked ₊4 or ₋4 numbers.
Learn more about Equations here:
https://brainly.com/question/22688504
#SPJ9
I need help please but if you can give me the step by step it would be helpful thank you

Answers
Answer: (x^2 -6x +10)(x - 2)
All the steps are shown in the picture below:

For her party can Nina fill fewer than 10 bags with treats between 10 and 20 bags between 20 and 30 bags or more than 30 bags explain
Answers
The correct option regarding the number of bags filled by Nina, using proportions, is given as follows:
Between 20 and 30 bags.
What is a proportion?A proportion is a fraction of an amount, and this fraction is combined with the unit rates of the problem and basic arithmetic operations, especially multiplication and division, to find the desired amounts in the context of the problem.
In this problem, a proportion is applied to find the number of bags filled by Nina, which is given by the division presented as follows:
Number of bags = Number of treats / Treats per bag.
The values of these parameters are given as follows:
Number of treats: 78.Number of treats per bag: 3.Hence the numeric value of the expression is:
Number of bags = 78/3 = 26.
Which is a number between 20 and 30.
Missing InformationThe problem states that Nina had 78 treats, and each bag has 3 treats, then it asks the correct option regarding the number of bags.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
need help with this

Answers
Answer:
r = √(3V/(πh))r ≈ 1.78 cmStep-by-step explanation:
Multiply by the inverse of the coefficient of r², then take the square root.
\(V=\dfrac{1}{3}\pi r^2h\\\\V=\dfrac{\pi h}{3}r^2\\\\r^2=\dfrac{3V}{\pi h}\\\\\boxed{r=\sqrt{\dfrac{3V}{\pi h}}}\)
For V=50, h=15, this is ...
\({r=\sqrt{\dfrac{3(50)}{\pi(15)}}=\sqrt{\dfrac{10}{\pi}}\approx\boxed{1.78\quad\text{cm}}\)
Given the individual rates of workers, to find the combined rate of all the individuals working together you must
the individual rates.
Fill in the blank

Answers
To find the combined rate of all the individuals working together, you must add the individual rates.
How to calculate combined rate of individuals working together?When calculating the combined rate of individuals working together, you need to add up the individual rates. Each worker contributes their own rate of work or productivity, and by adding these rates together, you can determine the combined rate at which they are working collectively.
This allows you to assess the overall efficiency and output of the team or group. By summing up the individual rates, we have better understanding of the overall productivity and performance of the group.
Read more about individual rates
brainly.com/question/31251379
#SPJ1
What is the mid point of the x intercept of f(x)=(x-4)(x+4)
Answers
Answer:
(0, 0)
Step-by-step explanation:
f(x) = (x-4)(x+4)
Let f(x) = 0
Therefore,
(x-4)(x+4) = 0
x - 4 = 0 or x + 4 = 0
x = 4 or x = - 4
Hence x - intercepts are (-4,0) & (4, 0)
Mid point of x - intercepts = (- 4 + 4) /2, (0+0)/2= 0/2 , 0/2 = (0, 0)