Two integers, a and b, have a greatest common
actor of 1. If a = 12 and b is greater than 35
but no more than 40, what is the value of b?
Answers
The value of the integer of the b is 37,38,39.
According to the statement
We have to find that the value of the integers.
So, For this purpose, we know that the
An integer is a number with no decimal or fractional part and it includes negative and positive numbers, including zero.
From the given information:
Two integers, a and b, have a greatest common actor of 1. If a = 12 and b is greater than 35 but no more than 40.
Then
a=12
35 < b < 40
Now, we use the GCF
then
GCF of a and b = 1
GCF of 12 and 37 = 1
GCF of 12 and 38 = 2
GCF of 12 and 39 = 3 .
So, The value of the integer of the b is 37,38,39.
Learn more about integer here
https://brainly.com/question/12399107
#SPJ9
Related Questions
Expand and simplify 3(2 + √5)
Answers
Answer:
6+3√5(Decimal: 12.708204)
Step-by-step explanation:
3(2+√5)
=6+3√5(Decimal: 12.708204)
What is an example of slope-intercept form?.
Answers
Answer:
y = 3x + 1
Step-by-step explanation:
The equation for slope-intercept form is y=mx+b, where m is the slope and b is the y-intercept.
How do you dilate by a scale factor of 3?
Answers
To dilate by scale factor of 3, you have to measure the original vertical and horizontal from the point to the center of dilatation then multiply or divide it with 3. After that, starting from the center of dilatation move the point with the divide or multiply result.
What is dilatation?Dilatation is a process of enlarging or decreasing a figure without changing its original shape. When you are going to decrease the size of the figure. you will divide the original point with the scale point and vice versa. As a note, the center of dilatation is a fixed point where the figure is dilated. On every dilated figure, you can only make one center of dilatation.
Learn more about dilatation here
https://brainly.com/question/30103195
#SPJ4
Suppose that X is a Poisson random variable with λ=45. Round
your answers to 3 decimal places (e.g. 98.765). (a) Compute the
exact probability that X is less than 30.
Answers
The exact probability that a Poisson random variable X with a rate parameter λ=45 is less than 30 can be calculated using the cumulative distribution function (CDF) of the Poisson distribution. The CDF gives the probability of obtaining a value less than or equal to a given value. In this case, we need to find P(X < 30).
To compute this probability, we can use the formula for the Poisson CDF:
P(X < 30) = Σ(k=0 to 29) e^(-λ) * (λ^k) / k!
where λ is the rate parameter (in this case, λ=45) and k represents the number of events. We sum up the probabilities of all possible values of k from 0 to 29.
Substituting the values into the formula, we get:
P(X < 30) = Σ(k=0 to 29) e^(-45) * (45^k) / k!
Calculating this sum will give us the exact probability that X is less than 30, rounded to 3 decimal places.
Learn more about probability click here: brainly.com/question/31828911
#SPJ11
The outputs of an organization, divided by all of its inputs, is called its:
A. total factor productivity.
B. total labor productivity.
C. partial productivity.
D. total capital productivity.
E. efficiency ratio.
Answers
Total factor productivity. This term refers to the ratio of an organization's outputs to all of its inputs, including labor, capital, and other resources. This measurement is used to determine how efficiently an organization is using its resources to produce its desired outcomes.
An explanation of the other options is as follows:
- B. Total labor productivity refers only to the output of an organization divided by its labor inputs.
- C. Partial productivity measures the output of an organization relative to a single input factor, such as labor or capital.
- D. Total capital productivity measures an organization's output relative to its capital inputs.
- E. Efficiency ratio is a broader term that can refer to any ratio that measures an organization's efficiency in achieving its goals, but it does not specifically refer to the ratio of outputs to inputs.
total factor productivity is the most appropriate answer to the question as it measures the overall efficiency of an organization in using all of its resources to achieve its goals.
To know more about measurement , visit:
https://brainly.com/question/4725561
#SPJ11
Sabiendo que la velocidad del sonido es de 343. 2 m/s, ¿a cuántos kilómetros de distancia se produce un trueno que tarda 6 segundos en oÃrse?
Answers
2.0592 kilometers away is a clap of thunder that takes 6 seconds to be heard.
When you hear thunder, you are actually hearing sound waves created by lightning.
Light travels much faster than sound, so you usually see lightning first and hear the thunder a few seconds later. By measuring the time between lightning strikes, you can estimate how far lightning has struck.
The speed of sound is approximately 343.2 meters per second in dry air at 20 degrees Celsius. So if it takes him 6 seconds for lightning to reach him, the lightning will be:
distance = speed x time
Distance = 343.2m/s x 6s
distance = 2059.2 meters
So the lightning struck about 2059.2 meters away from you. To convert this to kilometers, divide by 1000.
Distance = 2059.2m / 1000
distance = 2.0592 km
Therefore, lightning struck about 2.0592 kilometers away.
the question in English:
Knowing that the speed of sound is 343.2 m/s, how many kilometers away is a clap of thunder that takes 6 seconds to be heard?
learn more about light
brainly.com/question/31064438
#SPJ4
HELP PLEASE I NEED TO SOLVE THIS 1 PROBLEM BUT I DONT KNOW IT PLEASE HELP

Answers
Answer:
D. 3
Step-by-step explanation:
sub 3 into problem you get a zero
7) 5(r + 2) = 8 + 57
Answers
Step-by-step explanation:
5r + 10 = 65
5r =65 - 10
r = 55/5
r = 11
Answer:
r=11
Step-by-step explanation:
you first have to work with the brackets and then group the like terms
5(r+2)=8+57
5r+10=65
5r/5=65-10
5r/5=55/5
r=11
I hope this helps
si d dx is convergent. True O False
If f is continuous on [0, [infinity]o), and if f f (x) da is convergent, then ° ƒ (x) dx is convergent. True False
Answers
The statement "If f is continuous on [0, ∞) and if ∫f(x) dx is convergent, then ∫f'(x) dx is convergent" is true.
The integral of a continuous function over a given interval converges if and only if the function itself is bounded on that interval. If f(x) is continuous on [0, ∞) and its integral converges, it implies that f(x) is bounded on that interval. Since f'(x) is the derivative of f(x), it follows that f'(x) is also bounded on [0, ∞). As a result, the integral of f'(x) over the same interval, ∫f'(x) dx, is convergent.
The statement is a consequence of the fundamental theorem of calculus, which states that if a function f is continuous on a closed interval [a, b] and F is an antiderivative of f on [a, b], then ∫f(x) dx = F(b) - F(a). In this case, if ∫f(x) dx converges, it implies that F(x) is bounded on [0, ∞). Since F(x) is an antiderivative of f(x), it follows that f(x) is bounded on [0, ∞) as well.
As f(x) is bounded, its derivative f'(x) is also bounded on [0, ∞). Therefore, the integral of f'(x) over the same interval, ∫f'(x) dx, is convergent. This result holds under the assumption that f(x) is continuous on [0, ∞) and that ∫f(x) dx converges.
Learn more about antiderivative here:
https://brainly.com/question/31396969
#SPJ11
Find the area of the region inside the inner loop of the limaçon r=3−6cosθ.The area of the region is? (Use pi as needed)
Answers
Answer: Therefore, the area of the region inside the inner loop of the limaçon r = 3 - 6 cosθ is approximately 14.14 square units.
Step-by-step explanation: The limaçon is given by the equation r = 3 - 6 cosθ.
The inner loop of the limaçon occurs when 0 ≤ θ ≤ π, where r = 3 - 6 cosθ is positive.
To find the area of the region inside the inner loop, we need to integrate the expression for the area inside a polar curve, which is given by the formula A = 1/2 ∫[a,b] r^2(θ) dθ.
For the inner loop of the limaçon, we have a = 0, b = π, and r = 3 - 6 cosθ. Therefore, the area of the region inside the inner loop is:
A = 1/2 ∫[0,π] (3 - 6 cosθ)^2 dθ
= 1/2 ∫[0,π] (9 - 36 cosθ + 36 cos^2θ) dθ
= 1/2 [9θ - 36 sinθ + 12 sin(2θ)]|[0,π]
= 1/2 [9π]
= 4.5π
Hope this Helps :D
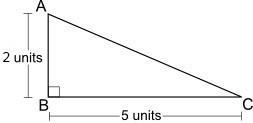
The area of the triangle above will equal one half of a rectangle that is 5 units long and units wide. (Input only whole numbers, such as 8.) (1 point)
Answers
Answer:
Width of the rectangle is 2Step-by-step explanation:
A rectangle can is made up of two right angled triangle as shown.
Since area of a rectangle = \(base * height\)
Area of one of the triangle = \(\frac{1}{2}\ * \ area\ of\ the\ rectangle\)
The length and width of the triangle will be the same as that of the rectangle i.e 5units long and 2units wide
Area of one of the triangle = \(\frac{1}{2} * 5 * 2\)
Area of one of the triangle = 5units²
The area of the triangle above will equal one half of a rectangle that is 5 units long and 2 units wide.
Mathematics
Simple events likelihood experimental probability

Answers
Problem 1
Answer: Closer to 1
Explanation:
There are 20 gumballs total. Half of this is 20/2 = 10 gumballs. If there's more than 10 of one color, then the probability of getting that color is closer to 1, than it is to 0. Here we have 12 pink which is greater than 10, so that's why the answer is closer to 1.
================================================
Problem 2
Answer: Closer to 0
Explanation:
The amount of green (3) is less than 10, so that's why the probability is closer to 0 than it is to 1. We can see that 3/20 = 0.15 is less than 0.50
================================================
Problem 3
Answer: Closer to 0
Explanation:
We have a similar situation compared to problem 2. This time we have 5/20 = 0.25 which is less than 0.50
================================================
Problem 4
Answer: 48% chance; fairly likely
Explanation:
We have 12 green out of 25 total, so the probability of choosing green is 12/25 = 0.48 = 48%. While this probability is not over 50%, I still say it's fairly likely considering the other colors lead to smaller probabilities. For instance, purple has a chance of 6/25 = 0.24 = 24% and orange has a probability of 2/25 = 0.04 = 4%, both of which are smaller than 48%
DEF Company's current share price is $16 and it is expected to pay a $0.55 dividend per share next year. After that, the firm's dividends are expected to grow at a rate of 3.7% per year. What is an estimate of DEF Company's cost of equity? Enter your answer as a percentage and rounded to 2 DECIMAL PLACES. Do not include a percent sign in your answer. Enter your response below. -7.1375 正确应答: 7.14±0.01 Click "Verify" to proceed to the next part of the question.
DEF Company also has preferred stock outstanding that pays a $1.8 per share fixed dividend. If this stock is currently priced at $27.6 per share, what is DEF Company's cost of preferred stock? Enter your answer as a percentage and rounded to 2 DECIMAL PLACES. Do not include a percent sign in your answer. Enter your response below.
Answers
An estimate of DEF Company's cost of equity is 7.14%.
What is the estimate of DEF Company's cost of equity?To estimate the cost of equity, we can use the dividend growth model. The formula for the cost of equity (Ke) is: Ke = (Dividend per share / Current share price) + Growth rate
Given data:
The dividend per share is $0.55, the current share price is $16, and the growth rate is 3.7%.The cost of equity iss:
Ke = ($0.55 / $16) + 0.037
Ke ≈ 0.034375 + 0.037
Ke ≈ 0.071375.
Read more about cost of equity
brainly.com/question/13086476
#SPJ4
Both the cost of equity and the cost of preferred stock play important roles in determining a company's overall cost of capital and the required return on investment for different types of investors.
To estimate DEF Company's cost of equity, we need to calculate the dividend growth rate and use the dividend discount model (DDM). The cost of preferred stock can be found by dividing the fixed dividend by the current price of the preferred stock.
The calculations will provide the cost of equity and cost of preferred stock as percentages.
To estimate DEF Company's cost of equity, we use the dividend growth model. First, we calculate the expected dividend for the next year, which is given as $0.55 per share.
Then, we calculate the dividend growth rate by taking the expected growth rate of 3.7% and converting it to a decimal (0.037). Using these values, we can apply the dividend discount model:
Cost of Equity = (Dividend / Current Share Price) + Growth Rate
Plugging in the values, we get:
Cost of Equity = ($0.55 / $16) + 0.037
Calculating this expression will give us the estimated cost of equity for DEF Company as a percentage.
To calculate the cost of preferred stock, we divide the fixed dividend per share ($1.8) by the current price per share ($27.6). Then, we multiply the result by 100 to convert it to a percentage.
Cost of Preferred Stock = (Fixed Dividend / Current Price) * 100
By performing this calculation, we can determine DEF Company's cost of preferred stock as a percentage.
Learn more about cost of equity from the given link:
https://brainly.com/question/23968382
#SPJ11
In a model of a construction project, 1 yard is represented as 0.25 inch. What would be the actual area of a garden in square yards, if it is represented by 20 square inches in the model?
Answers
1 yard : 0.25 inch
Actual Area: Model Area
(1)^2 : (0.25)^2
1 square yard: 0.0625 square inch
0.0625 square inch — 1 square yard
20 square inches — 1/0.0625 x 20
= 320 square yards
Therefore the actual area of a garden is 320 square yards.
What is a test statistic example?
Answers
The test statistic for a Z-test is the Z-statistic, which has the standard normal distribution under the null hypothesis
In statistics, what is a test statistic?A test statistic shows how closely your data’s distribution fits the distribution anticipated by the statistical test’s null hypothesis. The frequency with which each observation happens is defined by the distribution of data, which may be represented by its central tendency and variance around that central tendency.
Z= (x – y)/(x2/n1 + y2/n2) is the formula for calculating the test statistic when comparing two population means. To compute the statistic, we must first compute the sample means (x and y) and standard deviations (x and y) for each sample independently. In statistics, there are many different types of tests, such as the t-test, Z-test, chi-square test, anova test, binomial test, one sample median test, and so on. If parametric tests are applied,
To learn more about test statistics to refer:
https://brainly.com/question/17152773
#SPJ4
Multiply.
(−2.1)⋅(−1.4)
−29.4
−2.94
2.94
29.4
Answers
Answer:
2.94
Step-by-step explanation:
multiply them like normal multiplication
remember that 2 negatives equal positive
-2.1•-1.4= 2.94
The answer is not negative since the rule is, if your multiplying two negative numbers the product is positive
In ARST, the measure of ZT=90°, the measure of ZR=6°, and RS = 3.6 feet. Find thelength of ST to the nearest tenth of a foot.S3.6XN60T70
Answers
we have taht
sin(R)=ST/SR -----> by opposite side divided by the hypotenuse
substitute given values
sin(6)=x/3.6
solve for x
x=3.6*sin(6)
x=0.4 ftAssume that police estimate that 23% of drivers do not wear their seatbelts. They set up a safety roadblock, stopping cars to check for seatbelt use. They stop 20 cars during the first hour a. Find the mean, variance, and standard deviation of the number of drivers expected not to be wearing seatbelts. Use the fact that the mean of a geometric distribution is pi = 1/p and the variance is ohm^2 = p/q^2? b. How many cars do they expect to stop before finding a driver whose seatbelt is not buckled?
Answers
The mean of the number of drivers expected not to be wearing seatbelts is approximately 4.35, the variance is approximately 15.62, and the standard deviation is approximately 3.95 and they expect to stop approximately 4.35 cars before finding a driver whose seatbelt is not buckled.
a. To find the mean, variance, and standard deviation of the number of drivers expected not to be wearing seatbelts, we can model the situation using a geometric distribution.
Let's define a random variable X that represents the number of cars stopped until the first driver without a seatbelt is found. The probability of a driver not wearing a seatbelt is given as p = 0.23.
The mean (μ) of a geometric distribution is given by μ = 1/p.
μ = 1/0.23 ≈ 4.35
The variance (σ^2) of a geometric distribution is given by σ^2 = q/p^2, where q = 1 - p.
σ^2 = (0.77)/(0.23^2) ≈ 15.62
The standard deviation (σ) is the square root of the variance.
σ = √(15.62) ≈ 3.95
b. The expected number of cars they expect to stop before finding a driver whose seatbelt is not buckled is equal to the reciprocal of the probability of success (finding a driver without a seatbelt) in one trial. In this case, the probability of success is p = 0.23.
Expected number of cars = 1/p = 1/0.23 ≈ 4.35
To learn more about mean, variance and standard deviation go to:
https://brainly.com/question/30558769
#SPJ11
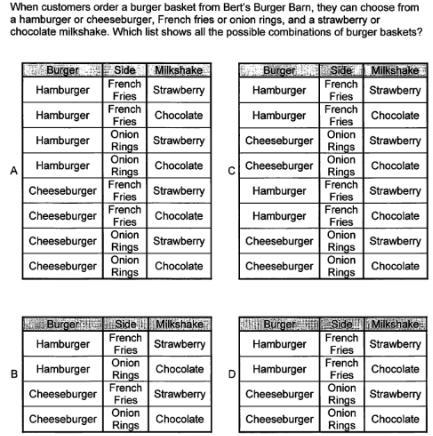
The sample space listing the eight simple events that are possible when a couple has three children is {bbb, bbg, bgb, bgg, gbb, gbg, ggb, ggg}. After identifying the sample space for a couple having four children, find the probability of getting four girls and no boys.
Identify the sample space for a couple having four children.
(Use a comma to separate answers as needed. )
Answers
A 0.25 = 25% probability of having three females and one guy is discovered using probability & sample space ideas (in any order ).
The set containing all potential outcomes is known as the sample space.
The proportion of intended results in the sample space multiplied by the total of possibilities is the probability estimated from the sample space.
The sample space for 4 kids is provided by:
B - B - B - B
B - B - B - G
B - B - G - B
B - B - G - G
B - G - B - B
B - G - B - G
B - G - G - B
B - G - G - G
G - B - B - B
G - B - B - G
G - B - G - B
G - B - G - G
G - G - B - B
G - G - B - G
G - G - G - B
G - G - G - G
There are 16 possibilities.
There are 3 girls and 1 guy in the four groups, which are B-G-G-G, G-B-G-G, G-G-B-G, & G-G-G-B.
In other words, the likelihood of having three girls & one male is 25% when p = D T = 4 16 = 0.25 0.25 (in any order).
Learn more about the probability at
https://brainly.com/question/14924566?referrer=searchResults
#SPJ4
Can someone help me?
Answers
B.
It lists every possible option
Answer:
The answer is A it lists every possible option
The sum of interior angles of a regular polygon is 24 times the size of exterior angle. Find number of sides of the polygon
Answers
Answer:
n = 50
Step-by-step explanation:
The sum of interior angles of a regular polygon is 24 times the size of exterior angle. Find number of sides of the polygon
let the sum of exterior be e
Let the sum of interior be i
IF the sum of interior angles of a regular polygon is 24 times the size of exterior angle, then;
i = 24e
Also sum of exterior angle = 360/n
i + e = 180
24e + e = 180
25e = 180
e = 180/25
e = 7.2
since sum of exterior angle = 360/n
7.2 = 360/n
n = 360/7.2
n = 50
The number of sides is 50
the average service rate at an automatic teller is 15 customers per hour and a customer arrives on average about every 10 minutes. on average, how many customers are in the queue at any one time?
Answers
The number of customers in the queue at any one time will be 0.205.
From the poisson process,formula for the required probability will be,
P(r,n) = (r t)ne-r t/n!
here , r = rate of customers per hour
As, 1 hour = 60 minutes
r =15 customers per 60 minutes
t = time in minutes
n = number of customers
Therefore, from the given question we can write, r = 1/4
And for n = 1 , t = 10
Therefore, from the equation, we can write
P(10,1) = (¼ x 10 ) 1 x e-¼ x 10/1!
P(10,1) = 5/2 x e-5/2
= 5/2 e-5/2
= 5/2 x 0.08209
= 0.205
Therefore, required number of customers is 0.205
To know more about poisson process, visit here:
https://brainly.com/question/28085239
#SPJ4
Which equation is modeled below?
4 x tiles and 2 negative 1 tiles = 2 x tiles and 4 1 tiles.
2 x + (negative 2) = negative 2 x + 6
4 x + (negative 2) = negative 2 x + 6
2 x + 4 = 6 x + 2
Negative 2 x + 4 = 6 x + (negative 2)
(Ignore the filled in bubble)

Answers
Answer:
B
Step-by-step explanation:
4 (x) + 2 (-1) = 2 (-x) + 6(1)
4x + -2 = -2x + 6
The equation for the given figure is 4x-2=-2x+6. Therefore, option B is the correct answer.
What is an equation?In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.
From the given figure,
x+x+x+x+(-1-1)=(-x-x)+(1+1+1+1+1+1)
⇒ 4x-2=-2x+6
So, equation modeled as 4x-2=-2x+6
The equation for the given figure is 4x-2=-2x+6. Therefore, option B is the correct answer.
To learn more about an equation visit:
https://brainly.com/question/14686792.
#SPJ6
which expression fails to compute the area of a triangle having base b and height h (area is one-half base time height)?a.(1.0 / 2.0 ) * b * hb.(1 / 2) * b * hc.(b * h) / 2.0d.0.5 * b * h
Answers
The expression that fails to compute the area of a triangle correctly is option b: (1 / 2) * b * h.
The correct formula to compute the area of a triangle is one-half times the base multiplied by the height, which can be written as (1/2) * b * h. Option a, c, and d correctly represent this formula. However, option b is incorrect because it uses integer division instead of decimal division.
In option b, (1 / 2) is computed using integer division, which results in truncating the decimal part. Therefore, (1 / 2) evaluates to 0 instead of 0.5. As a result, the expression (1 / 2) * b * h would yield incorrect and significantly smaller results than the actual area of the triangle.
To accurately calculate the area of a triangle using this formula, it is essential to use decimal division or explicitly represent the fraction as a decimal. Options a, c, and d correctly account for this by using either 1.0/2.0 or 0.5, ensuring the proper calculation of the area.
Learn more about area of a triangle here:
https://brainly.com/question/27683633
#SPJ11
Consider the following IS-LM model: C=217+0.51Y D I=156+0.16Y−1,038i G=254 T=203 i=0.04 The IS equation is determined to be Y=1,586.27−3,145.45. The LM equation is given as i=0.04. Using the IS and LM equations, the equilibrium real output, Y, is (Round your response to the nearest integer.) Using the IS-LM model, the equilibrium value of consumption, C, is (Round your response to the nearest integer.)
Answers
In the given IS-LM model, the equilibrium real output, Y, and the equilibrium value of consumption, C, can be determined using the IS and LM equations. The IS equation relates output to the interest rate, while the LM equation represents the equilibrium condition in the money market. By substituting the given values into the equations, we can find the equilibrium values.
The IS equation is given by: Y = 1,586.27 - 3,145.45i.
The LM equation is given as: i = 0.04.
To find the equilibrium real output, we substitute the value of i from the LM equation into the IS equation:
Y = 1,586.27 - 3,145.45 * 0.04.
Calculating the right side of the equation, we have:
Y = 1,586.27 - 125.82,
Y ≈ 1,460.
Therefore, the equilibrium real output, Y, is approximately 1,460.
To find the equilibrium value of consumption, we substitute the equilibrium real output, Y, into the consumption function:
C = 217 + 0.51Y.
Substituting Y = 1,460, we have:
C = 217 + 0.51 * 1,460.
Calculating the right side of the equation, we find:
C ≈ 984.
Therefore, the equilibrium value of consumption, C, is approximately 984.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
Evaluate 1/2yz
if y= 3/5
and z= −1 7/8
Write your answer as a fraction in simplest form.
Answers
To evaluate 1/2yz when y = 3/5 and z = -17/8, we first substitute the given values for y and z into the expression:
1/2(3/5)(-17/8)
Next, we can simplify this by multiplying the fractions:
1/2 * 3/5 * -17/8 = (-3/10) * (-17/8)
To multiply the fractions we multiply the numerators and denominators separately:
(-3/10) * (-17/8) = (-3 * -17)/(10 * 8)
Then we can simplify the numerator by combining like terms:
(-3 * -17)/(10 * 8) = 51/40
So the final result of the expression is 51/40.
Answer:
_51/80
Step-by-step explanation:
1/2*3/5*_17/8
1/2×3/5×(_17/8)
3/10×(_17/8)
_51/80
There are 18 table at the venue. Total of 145 guests wil be attending the wedding. Are there enough tables?
Answers
Answer:
if there are at least 9 chairs at each table then yes
Step-by-step explanation:
this question might be something
so lets divide 145 by 18 to see how many seats at each table is required for everyone to fit
145/18
8.05555
and since we cant have 0.555 of a chair or person we round up to the nearest whole chair which is 9
hopes this helps please mark brainliest
Ok so lets start with the basics
We divide the 145 guests with 18 tables so we will get 8.055
So in normal questions we could tell the answer as 8.055 but what we will do here is since a human cant share 0.55 of a table we will round the answer off ..
If its is below five we will keep the answer as same as it is but if the number is above five we can round it off to the closest number which is 9 ..
So we can say the answer as 9.
the number of tickets sold for different concerts at a single venue in the past month. would you be more interested in looking at the mean, median, or mode? state your reasoning.
Answers
For analyzing the number of tickets sold for different concerts at a single venue in the past month, all three measures, mean, median, and mode, can provide useful information depending on the specific question we want to answer.
- The mean is the average number of tickets sold per concert, and it can help us understand the overall attendance at the venue. However, the mean can be skewed by a few high or low outliers, especially if there are some very popular or unpopular concerts that attract significantly more or fewer attendees than usual.
- The median is the middle value in the dataset, and it can help us identify the typical or typical range of ticket sales for concerts at the venue. The median is less affected by outliers than the mean, so it can be a more robust indicator of central tendency.
- The mode is the most frequent value in the dataset, and it can help us identify the most popular or least popular concerts at the venue. However, if there are several concerts with similar attendance numbers, there may not be a clear mode, or there may be multiple modes.
Therefore, it depends on the research question at hand, and all three measures should be considered together to gain a more complete understanding of the ticket sales for different concerts at a single venue in the past month.
Know more about the median
https://brainly.com/question/26177250
#SPJ11
Solve for Y
V = −4y + 4x
Answers
Answer:
Y=−4y/v +4x/v
Step-by-step explanation:
Divide each term in by v and simplify.
On a quiz there are four multiple-choice questions worth 3 points each and two true/false questionsworth 1 point each . Each multiple-choice question has five possible choices . If a student randomlyguesses on each question , what is the expected value of the student's score on the test ?
Answers
Answer:
The expected value of the student's score on the test is 3.4.
Step-by-step explanation:
Multiple choice questions:
worth 3 points.
Five possible choices, one of which is correct. So the expected value of the student in each multiple choice question is:
\(m = 3\frac{1}{5} = 0.6\)
True/false questions:
worth 1 point.
2 options, one of which is correct, so the expected value for each is:
\(t = 1\frac{1}{2} = 0.5\)
What is the expected value of the student's score on the test ?
4 multiple choice, two true-false. So
\(E = 4m + 2f = 4(0.6) + 2(0.5) = 2.4 + 1 = 3.4\)
The expected value of the student's score on the test is 3.4.