Answers
3/4, the negatives cancel each other out so you add them
Answer:
Use the number line and the additive inverse to find the difference.
Step-by-step explanation:
3/4
Related Questions
Which expression is equivalent to (5x^−5 y^3)^−2??
thanksss

Answers
Answer: I think its 1/5x^10y^-6
Step-by-step explanation:
please let me know if I'm wrong
Question is in the pic plz help

Answers
the size of a sample designed for dual-purpose testing should be
Answers
The size of a sample designed for dual-purpose testing should be determined based on several factors, including the specific objectives of the testing, the desired level of confidence, the acceptable margin of error, and the variability of the population being tested.
Dual-purpose testing typically involves testing for multiple purposes or criteria simultaneously, such as both quality control and compliance assessment.
In such cases, it is important to consider the requirements and constraints of each purpose and determine an appropriate sample size that satisfies both objectives.
To determine the sample size, statistical techniques can be used, such as power analysis or sample size calculation formulas.
These methods take into account the significance level, desired power, effect size, and variability of the variables under consideration. The specific formulas or approaches used may vary depending on the nature of the data and the statistical test being performed.
It is essential to strike a balance between the sample size and the resources available for testing.
A larger sample size generally provides more precise results but may require more time, effort, and resources. Conversely, a smaller sample size may be more practical but could result in less precise estimates.
Ultimately, the appropriate sample size for dual-purpose testing should be determined through careful consideration of the specific objectives, statistical requirements, available resources, and the trade-off between precision and practicality.
To know more about dual-purpose testing refer here:
https://brainly.com/question/32342682#
#SPJ11
What is negative times a negative?
Answers
Answer:
positive
Negative x negative = positive.
Here is an example:
-2 x -4 = 8.
Hope it helps!
positive
Negative x negative = positive.
Here is an example:
-6 x -2 = 12
Hope it helps!
Order these from least to greatest: .25, 3/8, 7/12, 5/16, .5
Answers
To make it easier change the fraction into decimals!
3/8 = .375
5/16 =.3125
7/12 = .583
.5 = 0.5
.25 = 0.25
So, according to my calculations I believe it goes like this: 0.25, 0.375, 0.3125, 0.5, .583
Really I am not sure if this is correct but I hope this helps you understand you can order it whatever way you want but make sure you understand the explanation :) have a great day!!
The sum of the angle measures of a triangle is 180°. Two angles of a triangle measure 40°and 60°, so Juan concludes that the third angle measures 80°. What do you notice about the how the conclusions were made from the statement above?
Answers
Answer:
Step-by-step explanation:
Third angle = 180 - (40 + 60)
= 180 - 100
= 80°
When you subtract the sum of 40 and 60 from 180, you will get the third angle.
factor x^2+64
and
factor 16x^2+49
Answers
Answer:
Step-by-step explanation:
x^2+64=(x+8i)(x-8i)
16x^2+49=(4x+7i)(4x-7i)
You randomly select one card from a 52-card deck. find the probability of selecting a red six or a black king.
Answers
The probability of randomly selecting a red six or a black king from a 52-card deck is 1/13.
To find the probability of selecting a red six or a black king from a 52-card deck, we need to determine the number of favorable outcomes (red six or black king) and divide it by the total number of possible outcomes (52 cards).
There are 2 red sixes (hearts and diamonds) and 2 black kings (spades and clubs) in a deck.
Since we want to select either a red six or a black king, we can add these numbers together to get a total of 4 favorable outcomes.
Since there are 52 cards in a deck, the total number of possible outcomes is 52.
Now, we can calculate the probability by dividing the number of favorable outcomes by the total number of possible outcomes: Probability = Number of favorable outcomes / Total number of possible outcomes Probability = 4 / 52 Probability = 1 / 13
Therefore, the probability of randomly selecting a red six or a black king from a 52-card deck is 1/13.
For more questions on probability
https://brainly.com/question/251701
#SPJ8
Find the center of the circle given by this equation:

Answers
Answer:
center of the circle is (5, -3) and radius of the circle is 8 units
Step-by-step explanation:
Find the center of the circle given by this equation:
x²-10x+y²+6y-30=0
for x
b= -10
for y
b=+6
complete the square
for x
(-10/2)² = 25
for y
(6/2)²=9
x²-10x+25
y²+6y+9
(x²-10x+25)+(y²+6y+9)+30=0+25+9
(x²-10x+25)+(y²+6y+9)=25+9+30
(x-5)²+(y+3)²=64
This is the form of a circle. Use this form to determine the center and radius of the circle
(x − h)² + (y − k)² = r²
Circle Equation
(x-a)² + (y−b) ² = r² is the circle equation with a radius r, centered at (a, b)
Rewrite x² - 10x + y² + 6y - 30 = 0 in the form of the standard circle equation
(x − h)² + (y − k)² = r²
(x - 5)² + (y-(-3))² = 8²
(x-5)² + (y+3)² = 8²
r=8
h=5
k=-3
signs of h and k are opposite of what they are inside the parenthesis
Match the values in this circle to those of the standard form. The variable r represents the radius of the circle, h represents the x- offset from the origin, and k represents the y-offset from origin.
r=8
h=5
k=-3
https://brainly.com/question/19375747
expii
Brian McLogan
Alex Federspiel
the college of arts and science at delta university has nine departments. the number of faculty in each department is shown below. what is the median number of faculty in the college of arts and science?
Answers
The median number of faculty in departments in the college of arts and science is 12.
The median is a measure of central tendency that represents the middle value of a dataset when the values are sorted in ascending or descending order. Its purpose is to give a single representative value for the dataset, offering a way to understand the center of the data distribution. Unlike the mean, which can be affected by extreme values, the median is resistant to outliers and gives us a better understanding of what a typical value in the data set might be.
To find the median number of faculty in the College of Arts and Science at Delta University, first, arrange the department faculty numbers in ascending order:
7, 8, 9, 11, 12, 13, 14, 15, 17.
Since there are nine departments, which is an odd number, the median will be the middle value in the sorted list. So the middle number is the fifth number, which is 12
The median number of faculty in departments in the College of Arts and Science at Delta University is 12, as it is the middle value in the sorted list.
Note: The question is incomplete. The complete question probably is: The college of arts and science at delta university has nine departments. The number of faculty in each department is shown below. What is the median number of faculty in departments in the college of arts and science? 8, 12, 9, 15, 17, 11, 13, 14, 7.
Learn more about Median:
https://brainly.com/question/26177250
#SPJ11
I need help with this, I'm terrible with graphs lol.
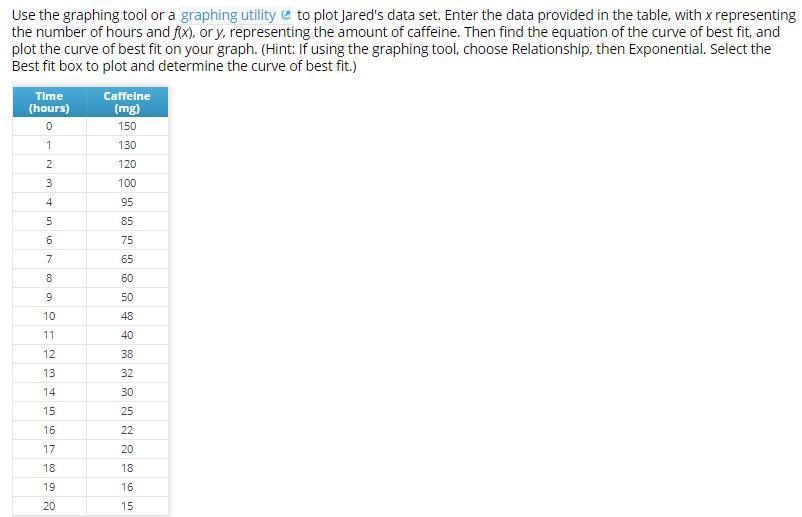
Answers
If f(x) = 1/9x - 2, what is f^-1 (x)
Answers
Greetings from Brasil...
For reverse function, just invert the X by the Y and vice versa.
Note that F(X) = Y and F⁻¹(X) = Y⁻¹
F(X) = 1(9X - 2) ⇔ Y = 1(9X - 2)
replacing X with Y⁻¹
X = 1(9Y⁻¹ - 2)
Y⁻¹ = (2X + 1)/9X
Which function represents the graph below?

Answers
will the sampling distribution of x overbarx always be approximately normally distributed? explain.
Answers
If these conditions are met, the sampling distribution of x will be approximately normally distributed. This is helpful in statistical analyses, as it allows us to make inferences about the population mean using the properties of the normal distribution.
The sampling distribution of x (the sample mean) will be approximately normally distributed if certain conditions are met. These conditions are based on the Central Limit Theorem (CLT), which states that:
1. The sample size (n) is large enough, typically n > 30. This ensures that the sampling distribution of x becomes more normally distributed as the sample size increases.
2. The population from which the sample is drawn is either normally distributed or the sample size is large enough to compensate for non-normality.
The sampling distribution of x overbarx (the sample mean) will be approximately normally distributed if certain conditions are met. These conditions include:
1. The population distribution must be normal or approximately normal.
2. The sample size should be large (typically n > 30).
3. The samples should be randomly selected from the population.
If these conditions are met, the sampling distribution of x will be approximately normally distributed. This is helpful in statistical analyses, as it allows us to make inferences about the population mean using the properties of the normal distribution.
Learn more about population mean:
brainly.com/question/30727743
#SPJ11
Find the present value of a sequence of annual payments of Rs 25000 each , the first being made at the end of 5th year and the last being paid at the end of 12th year, if money is worth 6%.
Answers
The present value of the sequence of annual payments of Rs 25000 each, the first being made at the end of the 5th year and the last being paid at the end of the 12th year, if money is worth 6% is Rs. 158620.39.
1: We can use the formula to calculate the present value of the annuity:
P = A x [1 - (1+i)^-n] / i
Where
P = Present Value
A = Annuity
i = Interest Raten = Number of payments
2: Calculate the present value of each payment using the formula:
P1 = 25000 / (1.06)⁵
P2 = 25000 / (1.06)⁶
P3 = 25000 / (1.06)⁷
P4 = 25000 / (1.06)⁸
P5 = 25000 / (1.06)⁹
P6 = 25000 / (1.06)¹⁰
P7 = 25000 / (1.06)¹¹
P8 = 25000 / (1.06)¹²
3: Substitute the values into the formula to find the present value:
P = P1 + P2 + P3 + P4 + P5 + P6 + P7 + P8
P = (25000 / (1.06)⁵) + (25000 / (1.06)⁶) + (25000 / (1.06)⁷) + (25000 / (1.06)⁸) + (25000 / (1.06)⁹) + (25000 / (1.06)¹⁰) + (25000 / (1.06)¹¹) + (25000 / (1.06)¹²)
P = 158620.39
Learn more about present value at
https://brainly.com/question/17010642
#SPJ11
factorise m²-14m+49
Answers
Answer:
(m-7\()^{2}\)
Step-by-step explanation:
A skateboard halfpipe is being designed for a competition. the halfpipe will be in the shape of a parabola and will be positioned above the ground such that its focus is 40 ft above the ground. using the ground as the x-axis, where should the base of the halfpipe be positioned? which equation best describes the equation of the halfpipe?
Answers
The equation of the halfpipe is Option A , (0, 20); Y equals one over eighty times x squared plus 20.
The equation of the halfpipe is Y = X²/80 +20.
What is parabola ?
A parabola is the set of points in a plane that are the same distance from a given point and a given line in that plane. The given point is called the focus, and the line is called the directrix. The midpoint of the perpendicular segment from the focus to the directrix is called the vertex of the parabola.The equation of parabola is given by
(X-h)² = 4p(Y-k)²
In this case h = 0
So we get
Y = X²/4P +k
Focus point is (h, p+k) , (p+k) = 40
Hence h, k = (0,20)
P = 40-k = 20
Equation Y = X²/80 +20
Therefore, the equation of the halfpipe is Y = X²/80 +20
Learn more about parabola
brainly.com/question/21685473
#SPJ4
The complete question is -
A skateboard halfpipe is being designed for a competition. The halfpipe will be in the shape of a parabola and will be positioned above the ground such that its focus is 20 ft above the ground. Using the ground as the x-axis, where should the base of the halfpipe be positioned? Which equation best describes the equation of the halfpipe?
(0, 20); y equals one over eighty times x squared plus 20
(0, 20); y equals one over eighty times x squared minus 20
(0, 10); y equals one over forty times x squared plus 10
(0, 10); y equals one over forty times x squared minus 10
List the data in the following stem-and-leaf plot. The leaf
represents the tenths digit.
14
0117
15
16
2677
17
9
18
8
Answers
The data listed from the stem-and-leaf plot is 14, 0.1, 0.1, 0.7, 15, 16, 26.6, 26.7, 27.7, 17, 0.9, 18, 0.8, 0.8. The stem "9" has a leaf value of 9, giving us 0.9.
(a) List the data in the following stem-and-leaf plot. The leaf represents the tenths digit.
The given stem-and-leaf plot represents a set of data, where the stem represents the tens digit and the leaf represents the tenths digit. To list the data, we need to combine the stem and leaf values.
The stem-and-leaf plot is as follows:
1 | 4
0 | 1 1 7
1 | 5
1 | 6
2 | 6 7 7
1 | 7
| 9
1 | 8
| 8
To list the data, we combine the stem and leaf values:
14, 0.1, 0.1, 0.7, 15, 16, 26.6, 26.7, 27.7, 17, 0.9, 18, 0.8, 0.8
Therefore, the data listed from the stem-and-leaf plot is:
14, 0.1, 0.1, 0.7, 15, 16, 26.6, 26.7, 27.7, 17, 0.9, 18, 0.8, 0.8.
In this stem-and-leaf plot, the stem values represent the tens digit, while the leaf values represent the tenths digit. Each stem value has one or more leaf values associated with it. To list the data, we combine the stem and leaf values to obtain the actual numbers.
For example, the stem "1" has leaf values of 4, 1, 1, 7, 5, and 6. Combining these with the stem, we get 14, 0.1, 0.1, 0.7, 15, and 16.
Similarly, the stem "2" has leaf values of 6, 6, 7, and 7. Combining these with the stem, we get 26.6, 26.7, and 27.7.
The stem "0" has leaf values of 1 and 1, which combine to form 0.1 and 0.1, respectively.
The stem "9" has a leaf value of 9, giving us 0.9.
Lastly, the stem "8" has a leaf value of 8, resulting in 0.8.
Combining all these values, we obtain the list of data: 14, 0.1, 0.1, 0.7, 15, 16, 26.6, 26.7, 27.7, 17, 0.9, 18, 0.8, 0.8.
Learn more about stem-and-leaf plot here
https://brainly.com/question/8649311
#SPJ11
Select each option that represents a proportional between x and y.
(50 points)
If get all correct (Brainliest)

Answers
Answer:
I think that is A and C and F
A large part of the answer has to do with trucks and the people who drive them. Trucks come in all different sizes depending on what they need to carry. Some larger trucks are known as 18-wheelers, semis, or tractor trailers. These trucks are generally about 53 feet long and a little more than 13 feet tall. They can carry up to 80,000 pounds, which is about as much as 25 average-sized cars. They can carry all sorts of items overlong distances. Some trucks have refrigerators or freezers to keep food cold. Other trucks are smaller. Box trucks and vans, for example, hold fewer items. They are often used to carry items over shorter distances.
A lot of planning goes into package delivery services. Suppose you are asked to analyze the transport of boxed packages in a new truck. Each of these new trucks measures12 feet × 6 feet × 8 feet. Boxes are cubed-shaped with sides of either1 foot, 2 feet, or 3 feet. You are paid $5 to transport a 1-foot box, $25 to transport a 2-foot box, and $100 to transport a 3-foot box.
How many boxes fill a truck when only one type of box is used?
What combination of box types will result in the highest payment for one truckload?
Answers
A truck can carry either 576 1-foot boxes, 72 2-foot boxes, or 21 3-foot boxes.
The combination of boxes that will result in the highest payment for one truckload is 89 1-foot boxes, 3 2-foot boxes, and 3 3-foot boxes, for a total payment of $3,422.
How to determine volume?To find how many boxes of one type will fill a truck, calculate the volume of the truck and divide it by the volume of one box.
Volume of the truck = 12 ft × 6 ft × 8 ft = 576 cubic feet
Volume of a 1-foot box = 1 ft × 1 ft × 1 ft = 1 cubic foot
Number of 1-foot boxes that will fill the truck = 576 cubic feet / 1 cubic foot = 576 boxes
Volume of a 2-foot box = 2 ft × 2 ft × 2 ft = 8 cubic feet
Number of 2-foot boxes that will fill the truck = 576 cubic feet / 8 cubic feet = 72 boxes
Volume of a 3-foot box = 3 ft × 3 ft × 3 ft = 27 cubic feet
Number of 3-foot boxes that will fill the truck = 576 cubic feet / 27 cubic feet = 21.33 boxes (rounded down to 21 boxes)
Therefore, a truck can carry either 576 1-foot boxes, 72 2-foot boxes, or 21 3-foot boxes.
To determine the combination of box types that will result in the highest payment for one truckload, calculate the total payment for each combination of box types.
Let x be the number of 1-foot boxes, y be the number of 2-foot boxes, and z be the number of 3-foot boxes in one truckload.
The volume of the boxes in one truckload is:
V = x(1 ft)³ + y(2 ft)³ + z(3 ft)³
V = x + 8y + 27z
The payment for one truckload is:
P = 5x + 25y + 100z
To maximize P subject to the constraint that the volume of the boxes does not exceed the volume of the truck:
x + 8y + 27z ≤ 576
Use the method of Lagrange multipliers to solve this optimization problem:
L(x, y, z, λ) = P - λ(V - 576)
L(x, y, z, λ) = 5x + 25y + 100z - λ(x + 8y + 27z - 576)
Taking partial derivatives and setting them equal to zero:
∂L/∂x = 5 - λ = 0
∂L/∂y = 25 - 8λ = 0
∂L/∂z = 100 - 27λ = 0
∂L/∂λ = x + 8y + 27z - 576 = 0
From the first equation, we get λ = 5.
Substituting into the second and third equations, y = 25/8 and z = 100/27. Since x + 8y + 27z = 576, x = 268/3.
Round these values to the nearest integer because no fraction for a box. Rounding down, x = 89, y = 3, and z = 3.
Therefore, the combination of boxes that will result in the highest payment for one truckload is 89 1-foot boxes, 3 2-foot boxes, and 3 3-foot boxes, for a total payment of $3,422.
Find out more on volume here: https://brainly.com/question/27710307
#SPJ1
Tasha has a gift card to buy tickets to the movie theater. The initial value of the gift card is $120 . The function M(x)=120-12x represents the amount of money, M , in dollars, that is still left on the gift card after purchasing x movie tickets at a cost of $12 each.
Complete the statements.
The value of is 60/-60 which is viable/not viable in terms of the given context.
Answers
The solution to the linear function M(x) = 180 is of x = -5.
What is a Linear Function Equation?The linear function equation is the slope-intercept form. Thus, it is expressed as f(x) = mx + b where m is the slope and b is the y-intercept of the line.
In this problem, the function is defined as follows:
M(x) = 120 - 12x.
M(x) represents the balance remaining on the gift card after x movie tickets priced at $12 are purchased.
The domain of the situation is given as follows:
x ≥ 0. {discrete}
As the number of tickets cannot assume negative neither decimal values.
The equation is:
M(x) = 180.
The solution is calculated as:
120 - 12x = 180
12x = -60
x = -60/12
x = -5.
Learn more about Linear function at:
https://brainly.com/question/21107621
#SPJ1
ayuda con esto ;v
9 6
- = -
6 X
Answers
Answer:
124 amigo dame corona no e tenido
A company makes and sells charm bracelets. The cost of producing x bracelets is represented by the function
C(x) = 180 + 8x. The revenue earned from selling x bracelets is represented by the function R(x) = 20x.
Write and simplify a function P that represents the profit made from selling x bracelets.
How many bracelets must the company sell to break even?
Answers
A function P that represents the profit made from selling x bracelets is
The number of bracelets this company must sell to break even is equal to 15 bracelets.
What is profit?In Mathematics, profit can be defined as a measure of the amount of money generated when the selling price is deducted from the cost price of a good or service, which is usually provided by producers.
Mathematically, the amount of profit made from selling x bracelets can be calculated by using the following function:
Profit made = Revenue earned – Cost of production
P(x) = R(x) - C(x)
P(x) = 20x - (180 + 8x)
P(x) = 20x - 180 - 8x
P(x) = 12x - 180
In order to break even, the number of bracelets that this company must sell would be calculated by equating the profit function to zero and solving for x as follows;
P(x) = 12x - 180
0 = 12x - 180
12x = 180
x = 180/12
x = 15 bracelets.
Read more on profit here: https://brainly.com/question/1717365
#SPJ1
3 times a number plus the quantity of two more than twice the number
Answers
Which of the following is equivalent to logb sqrt 57/74

Answers
Answer:
\(\log _b\left(\sqrt{\frac{57}{74}}\right)\) is equivalent to \(\frac{1}{2}\left(\log \:_b\left(57\right)-\log \:_b\left(74\right)\right)\).
Hence, option 'c' is true.
Step-by-step explanation:
Given the expression
\(\log _b\left(\sqrt{\frac{57}{74}}\right)\)
Rewrite as
\(=\log _b\left(\left(\frac{57}{74}\right)^{\frac{1}{2}}\right)\)
\(\mathrm{Apply\:log\:rule\:}\log _a\left(x^b\right)=b\cdot \log _a\left(x\right),\:\quad \mathrm{\:assuming\:}x\:\ge \:0\)
\(=\frac{1}{2}\log _b\left(\frac{57}{74}\right)\)
\(\mathrm{Apply\:log\:rule}:\quad \log _c\left(\frac{a}{b}\right)=\log _c\left(a\right)-\log _c\left(b\right)\)
\(=\frac{1}{2}\left(\log _b\left(57\right)-\log _b\left(74\right)\right)\) ∵ \(\log _b\left(\frac{57}{74}\right)=\log _b\left(57\right)-\log _b\left(74\right)\)
Therefore,
\(\log _b\left(\sqrt{\frac{57}{74}}\right)\) is equivalent to \(\frac{1}{2}\left(\log \:_b\left(57\right)-\log \:_b\left(74\right)\right)\).
Hence, option 'c' is true.
Solve by completing the square.
s2 + 22s = 27
Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.
Answers
Answer:
s = 1.17, -23.17
Step-by-step explanation:
s^2 + 22s = 27
Take the coefficient of s
22
Divide by 2
22/2 =11
Square it
11^2 =121
Add this to both sides
s^2 + 22s+121 = 27+121
s^2 + 22s+121 = 148
(s+11)^2 = 148
Take the square root of each side
sqrt((s+11)^2) = ±sqrt(148)
s+11 = ±sqrt(148)
Subtract 11 from each side
s+11-11 = -11 ±sqrt(148)
s = -11 ±sqrt(148)
s = -11 + sqrt(148) = 1.1655
- 11 - sqrt(148)=-23.166
Rounding to the nearest hundredth
s = 1.17, -23.17
Find. The value of x??

Answers
Answer:
5 is the value of X
Step-by-step explanation:
Hope it helps
let d 5 gcd(a, b). if a 5 da9 and b 5 db9, show that gcd(a9, b9) 5 1
Answers
gcd(a9, b9) = 1.
First, we know that d is a common factor of both a and b, because it is the greatest common divisor. So, we can write a = dm and b = dn for some integers m and n.
Now, let's consider a9 and b9. We can write them as:
a9 = 10da + a
b9 = 10db + b
where a and b are single digits (0-9).
We want to show that gcd(a9, b9) = 1.
Suppose there exists a common factor k > 1 of a9 and b9. Then, we have:
k | a9 and k | b9
So, we can write:
a9 = kp and b9 = kq for some integers p and q.
Substituting the expressions for a9 and b9, we get:
10da + a = kp and 10db + b = kq
Dividing both sides by d, we have:
10m + a/d = kp/d and 10n + b/d = kq/d
Since d is a factor of a and b, it must also be a factor of a/d and b/d. So, we can write:
a/d = dx and b/d = dy for some integers x and y.
Substituting these expressions, we get:
10m + dx = kp/d and 10n + dy = kq/d
Multiplying both sides by d, we have:
10dm + a = kp and 10dn + b = kq
But we already know that a = dm and b = dn, so we can substitute these expressions:
10a + a = kp and 10b + b = kq
Simplifying, we get:
11a = kp and 11b = kq
Since k > 1, either k = 11 or k > 11.
If k = 11, then we have:
a = 11p/11 = p
b = 11q/11 = q
But then we have a contradiction because we assumed that a and b are single digits (0-9).
If k > 11, then we have:
11a = kp > 11p and 11b = kq > 11q
But we know that a and b are single digits, so this is impossible.
Therefore, there cannot exist a common factor of a9 and b9 greater than 1. Hence, gcd(a9, b9) = 1.
To know more about common factors visit :
https://brainly.in/question/54144816
#SPJ11
Find the derivative of \( y \) with respect to \( x \) in the following: (a) \( y=(\ln x)^{\ln x} \) (b) \( y=\ln \left(\frac{\sqrt{x}}{1+\sqrt{x}}\right) \) (Hint for (a): use logarithmic differentiation"
Answers
The derivative of the function "y = 1/ln(x)" with respect to "x" is y' = -1/x(ln(x))².
To find the derivative of the function y = 1/ln(x) with respect to x, we use the quotient rule. The quotient rule states that if we have a function of the form f(x) = g(x)/h(x), then the derivative of f(x) with respect to x is given by:
f'(x) = (g'(x) * h(x) - g(x) * h'(x)) / (h(x))^2
In this case, g(x) = 1 and h(x) = ln(x). We find the derivatives of g(x) and h(x) first:
g'(x) = 0 (derivative of a constant is zero)
h'(x) = 1/x (derivative of ln(x) is 1/x)
Now we substitute these values into the quotient rule formula:
y' = (g'(x) × h(x) - g(x) × h'(x)) / (h(x))²
= (0 × ln(x) - 1 × (1/x)) / (ln(x))²
= -1/x(ln(x))²
Therefore, the required derivative is -1/x(ln(x))².
Learn more about Derivative here
https://brainly.com/question/31280680
#SPJ4
The given question is incomplete, the complete question is
Find the derivative of "y" with respect to "x" in y = 1/ln(x)
What additional information could be used to prove that ΔXYZ ≅ ΔFEG using ASA or AAS? Check all that apply.
Answers
The additional information required to prove that ΔXYZ and ΔFEG are congruent is ∠Z ≅ ∠G and XZ ≅ FG or ∠Z ≅ ∠G and XY ≅ FE. So option 1 and 5 are correct.
Here in the figure it is given that ∠F and ∠X are congruent. To prove the triangle is congruent we have to prove that either two sides including the angles are congruent or another angle and included side is congruent.
When ∠Z ≅ ∠G and XZ ≅ FG, two angles and included sides are congruent, so triangles are congruent.
∠Z ≅ ∠G and ∠Y ≅ ∠E , we can not apply ASA, since three angles are mentioned
XZ ≅ FG and ZY ≅ GE , Two sides are given, ASA cannot be applied, we need two angles
XY ≅ EF and ZY ≅ FG, is not possible.
∠Z ≅ ∠G and XY ≅ FE, one corresponding side and two angles are equal, so ΔXYZ ≅ ΔFEG according to ASA.
So, the correct answer is option 1 and option 5.
For more information regarding Congruency of triangle, kindly refer
https://brainly.com/question/30094434
#SPJ4
The complete question is as follows and image is given below
What additional information could be used to prove that ΔXYZ ≅ ΔFEG using ASA or AAS? Check all that apply.
∠Z ≅ ∠G and XZ ≅ FG
∠Z ≅ ∠G and ∠Y ≅ ∠E
XZ ≅ FG and ZY ≅ GE
XY ≅ EF and ZY ≅ FG
∠Z ≅ ∠G and XY ≅ FE

Answer:
1 and 5 are correct
Step-by-step explanation:
