Answers
Explaining
y= 3*-3
y=-9
Related Questions
When given a differential equation y'= f(y) where f is some function, one of the the things of interest is the set of points y where f(y) = 0. Why are they important? That is, what does knowing where f(y) = 0 tell you about the solutions y(t) of the differential equation? How do these points show up on the direction field?
Answers
When given a differential equation y'= f(y) where f is some function, the set of points y where f(y) = 0 is important because it provides information about the behavior of the solutions of the differential equation.What do we learn from the set of points y where f(y) = 0?
The set of points where f(y) = 0 provides us with information about the equilibrium solutions of the differential equation. These are solutions that are constant with time. The value of y at these points remains the same over time. For example, if f(y) = 0 for y = a, then y = a is an equilibrium solution. It will stay at the value a for all time.How do these points show up on the direction field?The direction field is a graphical representation of the differential equation. It shows the direction of the slope of the solutions at each point in the plane. To construct a direction field, we plot a small line segment with the slope f(y) at each point (t, y) in the plane. We can then use these line segments to get an idea of what the solutions look like.The set of points where f(y) = 0
shows up on the direction field as horizontal lines. This is because at these points, the slope of the solutions is zero. The direction of the solutions does not change at these points. Therefore, the solutions must be either constant or periodic in the neighborhood of these points.
to know more about equilibrium, visit
https://brainly.com/question/517289
#SPJ11
f(θ) = 2 cos(θ) + cos2(θ), 0 ≤ θ ≤ 2π
Answers
To find the maximum and minimum values of the given function f(θ), we need to find its critical points and endpoints.
First, we take the derivative of f(θ) with respect to θ:
f'(θ) = -2 sin(θ) - 2 cos(θ) sin(θ)
Setting f'(θ) = 0, we get:
-2 sin(θ) - 2 cos(θ) sin(θ) = 0
Simplifying and factoring out -2 sin(θ), we get:
-2 sin(θ) (1 + cos(θ)) = 0
This gives us two critical points: θ = 0 and θ = π.
Next, we need to evaluate the function at the endpoints of the given interval [0, 2π]:
f(0) = 2 cos(0) + cos2(0) = 3
f(2π) = 2 cos(2π) + cos2(2π) = 3
Now we compare the values of f(θ) at the critical points and endpoints to find the maximum and minimum values:
f(0) = 3 (endpoint)
f(π) = 1 (critical point)
f(2π) = 3 (endpoint)
Therefore, the maximum value of f(θ) is 3 and the minimum value is 1.
To learn more about trigonometric equation refer below
https://brainly.com/question/10676952
#SPJ11
Simplify 3xy+5yz-2xy +3yz
Answers
Answer:
8yz+xy
like terms and then solve it
The simplified expression is xy + 8yz
What is expression?Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between. The mathematical operators can be of addition, subtraction, multiplication, or division.
For example, x + y is an expression, where x and y are terms having an addition operator in between. In math, there are two types of expressions, numerical expressions - that contain only numbers; and algebraic expressions- that contain both numbers and variables.
An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division. The terms involved in an expression in math are:
Constant: A constant is a fixed numerical value.
Variable: A variable is a symbol that doesn't have a fixed value.
Term: A term can be a single constant, a single variable, or a combination of a variable and a constant combined with multiplication or division.
Coefficient: A coefficient is a number that is multiplied by a variable in an expression.
Given:
3xy+5yz-2xy +3yz
Now,
=3xy - 2xy + 5yz+ 3yz
=xy + 8yz
Hence, the simplifies expression is xy + 8yz.
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ2
Calculate the conversion to 2 decimal places.
How many pounds are in 2.8 kg of dog food?
Answers
There are approximately 6.17 pounds in 2.8 kg of dog food.
To convert 2.8 kg of dog food to pounds, we need to know the conversion factor between kilograms and pounds.
The conversion factor between kilograms and pounds is 1 kg = 2.20462 lbs.
To calculate the conversion, we can multiply the given weight in kilograms (2.8 kg) by the conversion factor:
2.8 kg * 2.20462 lbs/kg = 6.173636 lbs
Rounding to two decimal places, we get 6.17 lbs.
Therefore, there are approximately 6.17 pounds in 2.8 kg of dog food.
To summarize:
- Conversion factor: 1 kg = 2.20462 lbs
- Given weight: 2.8 kg
- Calculation: 2.8 kg * 2.20462 lbs/kg = 6.173636 lbs
- Rounded to two decimal places: 6.17 lbs
know more about decimal places,
https://brainly.com/question/20563248
#SPJ11
PLEASE HELP!!!!!!!!!!!!!
A handicapped ramp is being constructed for the front entrance of First National Bank in Springfield. ADA guidelines requires a rise angle from the foot of the ramp (point furthest from the entrance) not to exceed 4.8 degrees. This means the vertical to horizontal ratio cannot exceed 1:12. If the handicapped ramp must start 15 feet away from the front entrance, contractors estimate the rise to be about 3 feet.
Part A: Explain thoroughly whether or not these ramp dimensions meet the ADA guidelines.
Part B: If the rise estimate does not meet ADA requirements, provide a measurement that would meet the guidelines.
Answers
a) These ramp dimensions do not meet the ADA guidelines.
b) A measurement that would meet the guidelines is the ramp starting 39 feet away, with a height of 3 meters.
What is a slope?The slope of a situation is given by the vertical change divided by the horizontal change, and it's also the tangent of the angle of depression.
For the ramp in this problem, we have that the vertical change and the horizontal change are given as follows:
The vertical change is of: 3 feet.The horizontal change is of: 15 feet.The ratio between the vertical change to the horizontal change is of:
3/15 = 1/5.
Which is greater than 1/12, hence the ramp does not meet the ADA guidelines.
If the horizontal change was 13 times the vertical change, it would meet the ratio, hence a possible measurement is of:
3 feet vertical.39 feet horizontal.As the ratio would be of:
3/39 = 1/13 < 1/12.
More can be learned about the slope concept at https://brainly.com/question/18090623
#SPJ1
What is the measure of x?

Answers
Answer:
65⁰
Step-by-step explanation:
Take a look for the pict
Or
x+50⁰=115⁰
x= 115⁰-50⁰
x=65⁰

Which of the following expressions are equivalent to this expression
-1(0) = ?
0 -1[4 + (-4)]
-1[4 + (4)]
O 1 + [4 + (-4)]
O-11-4 + (-4)]
Answers
Answer:
so It A -1{4 + (-4)}
Step-by-step explanation:
take the quiz
![Which of the following expressions are equivalent to this expression-1(0) = ?0 -1[4 + (-4)]-1[4 + (4)]O](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/YjgLEQTCxiJA45TONDRJlaUbvaQ1Na25.jpeg)
2
Drag the tiles to the correct boxes to complete the pairs.
Find the surface area or the approximate surface area of each figure.
75 square inches
76 square inches
94 square inches
96 square inches
a triangular prism where the area of each
base is about 20 square inches the length
of each side of the base is 6 Inches, and
the height of the prism is 2 inches
a cube where the length of each edge is
4 inches
a rectangular prism with a length of 5 inches.
a width of 4 inches, and a height of 3 inches
a square pyramid with a base length and
slant height of 5 inches
Answers
To find the surface area of each figure, let's match the given values with the corresponding shapes: 75 square inches: Square pyramid with a base length and slant height of 5 inches.
76 square inches: Triangular prism where the area of each base is about 20 square inches, the length of each side of the base is 6 inches, and the height of the prism is 2 inches. 94 square inches: Rectangular prism with a length of 5 inches, width of 4 inches, and height of 3 inches. 96 square inches: Cube where the length of each edge is 4 inches. Therefore, the surface area of each figure is: 75 square inches: Surface area of the square pyramid = base area + (0.5 × perimeter of base × slant height) = (5^2) + (0.5 × 4 × 5) = 25 + 10 = 35 square inches. 76 square inches: Surface area of the triangular prism = 2 × (base area) + (perimeter of base × height) = 2 × 20 + (6 × 3) = 40 + 18 = 58 square inches.
94 square inches: Surface area of the rectangular prism = 2 × (length × width + length × height + width × height) = 2 × (5 × 4 + 5 × 3 + 4 × 3) = 2 × (20 + 15 + 12) = 2 × 47 = 94 square inches. 96 square inches: Surface area of the cube = 6 × (length of each edge)^2 = 6 × (4^2) = 6 × 16 = 96 square inches.
To learn more about surface area click here: brainly.com/question/29298005
#SPJ11
Some one pls help. And show steps in simple way. Urgently needed. Will give brainliest.

Answers
Answer: -4
Step-by-step explanation: The inverse operation means the opposite so what is the opposite of four? Negative four! Hope that helps!
Maria has 12 pieces of candy. She ate 1 of the pieces.
How many pieces of candy does Maria have left?

Answers
Answer:
The answer is 6 because 12 divided by 2 is 6 and 6 plus 6 is 12
Step-by-step explanation:
Answer:
c
Step-by-step explanation:
1/6 of 12=2 12-2=10 ez
If a matrix A is 5 x 3 and the product AB is 5 x 7, what is the size of B?
Answers
The size of the the matrix B if a matrix A is 5x3 and the product AB is 5x7 is B =[3x7].
Two matrices can only be multiplied if the first matrix has the same number of columns as the second matrix has. If the first matrix has dimensions of a x b and the second matrix has dimensions of c x d, then b = c and their product will have dimensions of a x d.
Let A is a 3 x 5 matrix and B is a 5 x 7 matrix
We know that matrix multiplication of A and B is possible if
Number of columns of A = Number of rows of B
Since in the given problem
Number of columns of A = Number of rows of B = 5
So the product is possible
Now the product AB is a matrix of order 3 × 7
Now the order of the product AB is 3 × 7
If a 3 x 5 matrix is multiplied by a 5 x 7 matrix then their product is a matrix of order 3 × 7.
Learn more about Matrix:
https://brainly.com/question/94574
#SPJ4
Find the mass of a ball of radius R if the mass density is
proportional to the product of the distance to the origin multiplied the distance to a
equatorial plane. Note that:
(i) A ball is a solid whose edge is a sphere.
(ii) An equatorial plane is any plane that contains the center of the sphere.
(iii) It is convenient to look for a coordinate system that facilitates the task. For example, the center of the ball can be placed at the origin. And the equatorial plane?need help with this calculus problem
Answers
The mass of the ball of radius R with the given mass density function is proportional to R^5.
To find the mass of the ball of radius R, we need to use the given mass density function. Let's assume that the center of the ball is at the origin and that the equatorial plane is the xy-plane.
We can use spherical coordinates to express the mass density function in terms of the radial distance, θ and φ. Since the density is proportional to the product of the radial distance and the distance to the equatorial plane, we have:
ρ(r,θ,φ) = kr^2cos(θ)
where k is a constant of proportionality.
The volume element in spherical coordinates is given by:
dV = r^2sin(θ)drdθdφ
To find the mass of the ball, we need to integrate the mass density over the volume of the ball:
M = ∫∫∫ ρ(r,θ,φ) dV
M = ∫∫∫ kr^2cos(θ) r^2sin(θ)drdθdφ
The limits of integration for r are 0 to R, for θ are 0 to π, and for φ are 0 to 2π.
M = k ∫∫∫ r^4cos(θ)sin(θ)drdθdφ from 0 to R, 0 to π, 0 to 2π
This integral can be evaluated using standard techniques. The final answer is:
M = (4/15)πkR^5
The mass of the ball of radius R with the given mass density function is proportional to R^5.
To learn more about sphere visit:
brainly.com/question/11374994
#SPJ11
14 to the 12th power divided by 14 to the 19th power
Answers
Answer:
14^12 = 56,693,912,375,296
14^19 = 5,976,303,958,948,914,397,184
56,693,912,375,296 / 9.4864506164219718946065961340209e-9
Please helpp absolute value
-|f| = -16
A) no solution
B) one solution
C) two solution
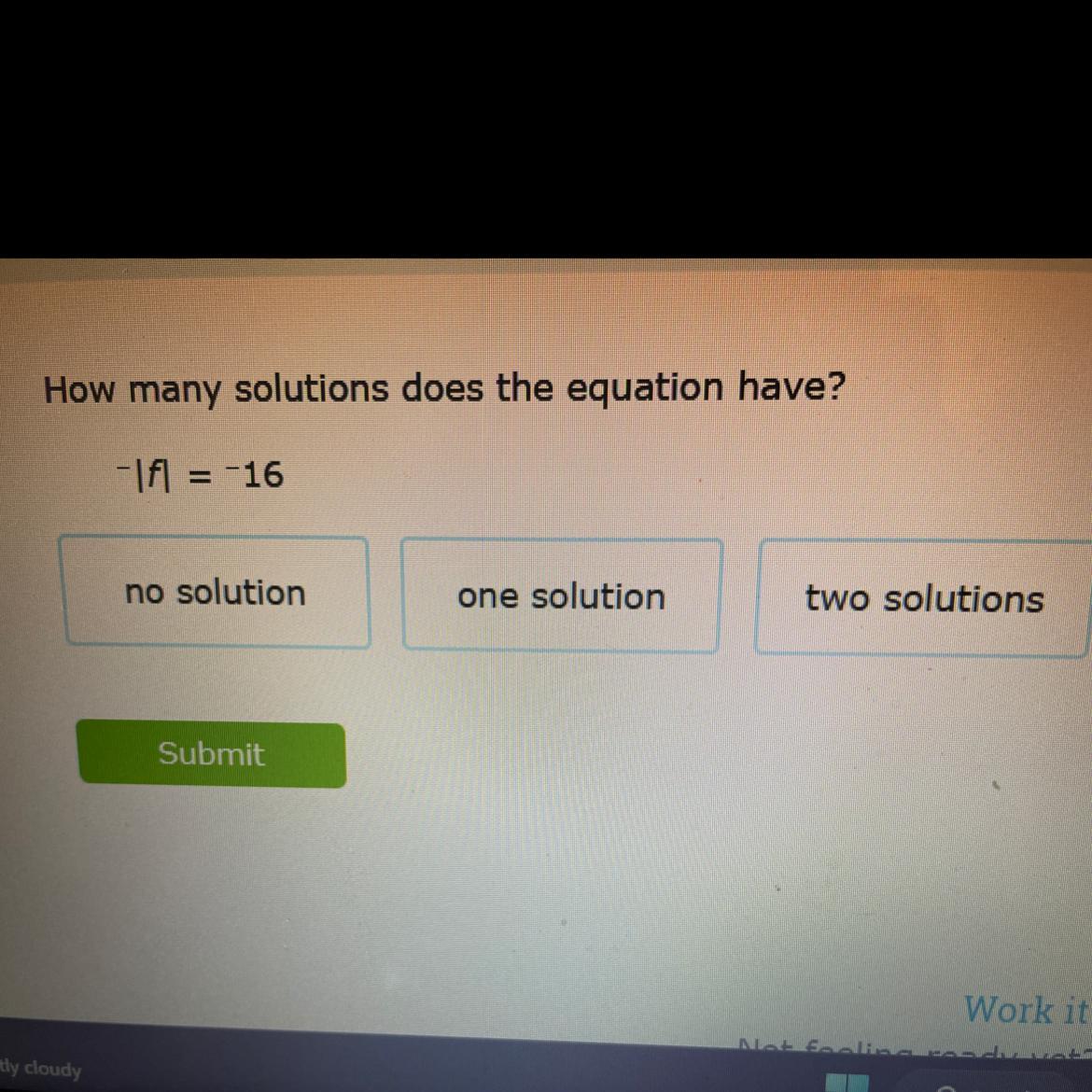
Answers
-1•-|f|=-16•-1
We are multiplying each side by -1 to cancel the negatives, but we will solve with them later. Remember, a negative number times a negative number equals a positive number.
|f|=16
Because absolute value measures the distance from 0 on a number line, there are two distances: a distance with a negative value and a distance with a positive value. So, if we must find a distance from 0, then a distance is -a and a.
|f|=16
f=-16 and 16
Now, let’s factor the negatives back into the equation
-|f|=-16
We know what f equals now, so we’ll input f=-16, 16 back into the equation:
-|-16|=-16
-(16)=-16
So, -16 is a solution. Now let’s check 16:
-|16|=-16
-(16)=-16
And, 16 is also a solution.
Answer: Therefore, the equation has two solutions.
The slope of a line is 1/2 and passes the point (2, -5)find the equation
Answers
THE GENERAL EQUATION OF A STRAIGHT LINE IS y=mx+c
TO FIND c I WILL SUBSTITUTE THE GIVEN KNOWN POINTS.
\( - 5= \frac{1}{2} (2) + c \\ - 5= 1 + c \\ c = - 5 - 1 \\ c = - 6\)
THEREFORE WE NOW HAVE
\( y= \frac{1}{2} x - 6\)
ATTACHED IS THE SOLUTION
Kono divides The numerator and the denominator of 4872 by the greatest common factor to simplify the fraction in one step by what number does he divide
Answers
Complete question:
Kono divides The numerator and the denominator of 48 over 72 by the greatest common factor to simplify the fraction in one step by what number does he divide
Answer:
2/3
Step-by-step explanation:
Given the number : 48 / 72
Obtain the greatest common factor of 48 and 72
- - - - 48 - - - - 72
- 2-- 24 - - - - 36
- 2 - 12 - - - - - 18
- 2 - 6 - - - - - - 9
- 3 - 2 - - - - - - 3
The greatest common factor of 48 and 72 is hence (2 * 2 * 2 * 3) = 24
Hence, divide both the numerator and denominator by 24 ;
Numerator = 48/24 = 2
Denominator = 72 / 24 = 3
= 2/3
The multiplicity of a root r of the characteristic equation of A is called the algebraic multiplicity of r as an eigenvalue of A. (true or false)
Answers
The multiplicity of a root r of the characteristic equation of A is called the algebraic multiplicity of r as an eigenvalue of A.
The above statement is True.
Eigenvalue:
An eigenvalue is a special set of scalar values associated with the most probable system of linear equations in a matrix equation. Eigenvectors are also called eigenvalues. It is a non-zero vector which can be modified by at most its scalar factor after applying a linear transformation.
According to the Question:
If the geometric multiple of the eigenvalues is greater than or equal to 2, the linearly independent set of eigenvectors is no longer unique to the multiple as before. For example, for the diagonal matrix A=[3003], one could also choose the eigenvectors [11] and [1−1], or any pair of two linearly independent vectors.
Sometimes vectors are simply expanded to vector times matrix. If this happens, this vector is called the eigenvector of the matrix and the "stretch factor" is called the eigenvalue. Example: Given a square matrix A, λ is the eigenvalue of A, and the corresponding eigenvector x is
Ax = λx.
Learn more about Eigenvalue:
https://brainly.com/question/29749542
#SPJ4
A car dealership sold 84 cars in April. The dealership wants to increase the number of cars sold by 25% in May. How many cars will the dealership need to sell to reach their goal?
Answers
Answer: 105 Cars
Step-by-step explanation: To get an increase of 25% you need to multiply 84 by .25 then add the product of that to 84 to get 105
The number of cars dealership need to sell to reach their goal is, 105 cars
What is the percentage?Percentage is a way to express a number as a fraction of 100. It is often used to represent ratios and proportions in a more convenient and understandable form, especially in financial and statistical contexts. For example, 50% means 50 per 100, or half of a given quantity. It is denoted using the symbol "%".
Given that,
A car dealership sold 84 cars in April,
The dealership wants to increase the number of cars sold by 25% in May
The number of cars dealership need to sell to reach their goal = ?
This represents a 25% increase, which is the same as adding one quarter to the original number of cars sold.
The car dealership wants to increase the number of cars sold by 25% in May, which means that they want to sell,
⇒ 84 x 1.25 = 105 cars
So, the dealership will need to sell 105 cars in May in order to reach their goal of increasing the number of cars sold by 25%.
To know more about Percentage check:
https://brainly.com/question/29306119
#SPJ6
What is one-fourth divided by 4 wholes
Answers
A baker regularly uses flour to make pastries for the bakery at the beginning of the month of the Baker has a 25 pound bag of flour. Each week she uses 5 3/5 pounds of flour write an expression to represent the change in weight of the bag of flour over four weeks
Answers
Answer:
At the beginning, she has 25lb of flour.
Each week, she ses (5 + 3/5) pounds of flour.
Then after the first week, she has a total of:
W(1) = 25lb - (5 + 3/5)lb
After another week, she has:
W(2) = 25lb - (5 + 3/5)lb - (5 + 3/5)lb = 25lb - 2*(5 + 3/5)lb
and so on.
if x represents the number of weeks, the equation is:
W(x) = 25lb - x*(5 + 3/5)lb
where x can be {0, 1, 2, 3, 4}
That is the equation that represents the change in the weight for the first four weeks.
HELP ME FAST!!! (It's about finding equations on graphs)

Answers
Answer:
y = 6x
Step-by-step explanation:
y - intercept is 0, because the line starts at y - value 0
The slope is 6/1 or 6 because as it rises 6 units, it also runs 1 unit
The equation is y = mx + b
m = slope
b = y - intercept
y = 6x + 0, or y = 6x
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Use the drawing tool(s) to form the correct answers on the provided number line. Plot the value(s) on the number line where this function is equal to zero: f(x) = (x + 5)(x − 1).
Its on a number line :)
Answers
Answer:
Step-by-step explanation:
Hope this Helps ;)

(-4, 6) and (3,-7)
Find the distance between each pair of points
Answers
Answer:
14.76482306
Step-by-step explanation:
distance equals the square root of (x2-x1)^2 + (y2-y1)^2.
think of your ordered pairs as set 1 and set 2. (-4, 6) would be set 1 and (3, -7) would be set 2. so your equation will look similar to: (3- -4)^2 + (-7-6)^2 then you square root the whole thing and you will have your answer.
25 POINTS AND BRAINLIEST PLEASE HELP
Q1 - A cell population grows at a rate of 30% every minute. It has a current population of 5,000. What will its population be 10 minutes from now.
Q2 - A town has an annual growth rate of 2%. In 1970, the population was 250 people. What was its population in 2020?
Answers
Answer:
ldldlldldlsñspleleldldkkfkdosos
Consider the Markov chain with the following transition matrix.
1/2 1/2 0
1/3 1/3 1/3
1/2 1/2 0
(a) Draw the transition diagram of the Markov chain.
(b) Is the Markov chain ergodic? Give a reason for your answer.
(c) Compute the two step transition matrix of the Markov chain.
(d) What is the state distribution π2 for t = 2 if the initial state distribution for t = 0 is π0 = (0.3, 0.45, 0.25)T ?
Answers
b) The Markov chain is both irreducible and aperiodic, it is ergodic.
c) The two-step transition matrix is:
\(\left[\begin{array}{ccc}1/4&1/4&0\\1/3&1/3&1/3\\1/2&1/2&0\end{array}\right]\)
d) The state distribution π2 for t = 2 is \(\left[\begin{array}{ccc}0.1575, 0.1575, 0.15\end{array}\right]\).
(a) The transition diagram of the Markov chain can be represented as follows:
\(1--\frac{1}{2}-- > 1\\|\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ |\\\frac{1}{3} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\\ |\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ |\\2--\frac{1}{2}-- > 3\\\)
(b) To determine if the Markov chain is ergodic, we need to check if it is both irreducible and aperiodic.
- Irreducibility: The Markov chain is irreducible if there is a positive probability of going from any state to any other state in a finite number of steps.
- Aperiodicity: A state is aperiodic if the greatest common divisor (GCD) of the number of steps required to return to the state is 1.
Since the Markov chain is both irreducible and aperiodic, it is ergodic.
(c) To compute the two-step transition matrix, we multiply the given transition matrix by itself:
\(\left[\begin{array}{ccc}1/2&1/2&0\\1/3&1/3&1/3\\1/2&1/2&0\end{array}\right] * \left[\begin{array}{ccc}1/2&1/2&0\\1/3&1/3&1/3\\1/2&1/2&0\end{array}\right] = \left[\begin{array}{ccc}1/4&1/4&0\\1/3&1/3&1/3\\1/2&1/2&0\end{array}\right]\)
So, the two-step transition matrix is:
\(\left[\begin{array}{ccc}1/4&1/4&0\\1/3&1/3&1/3\\1/2&1/2&0\end{array}\right]\)
(d) To find the state distribution π2 for t = 2, we multiply the initial state distribution π0 by the two-step transition matrix:
π0 = (0.3, 0.45, 0.25)T
π2 = π0 x two-step transition matrix
So, π2 = (0.3, 0.45, 0.25)T x \(\left[\begin{array}{ccc}1/4&1/4&0\\1/3&1/3&1/3\\1/2&1/2&0\end{array}\right]\)
π2 = \(\left[\begin{array}{ccc}0.3*1/4+0.45*1/3+0.25*1/2\\0.3*1/4+0.45*1/3+0.25*1/2\\0.3*0+0.45*1/3+0.25*0\end{array}\right]\)
π2 = \(\left[\begin{array}{ccc}0.1575, 0.1575, 0.15\end{array}\right]\).
Therefore, the state distribution π2 for t = 2 is \(\left[\begin{array}{ccc}0.1575, 0.1575, 0.15\end{array}\right]\).
Learn more about Markov Chain here:
https://brainly.com/question/30998902
#SPJ4
subject = Control System
Determine RHP roots in the following polynomial p(S)=S5 +S4 +25³ +35² +S+4
Determine RHP roots in the following polynomial p(S)=S5 +S4 +6S³ +6S² +255 +25
Answers
The solutions for the given problem are as follows:
\(p(S) = S5 + S4 + 25^3 + 35^2 + S + 4\) has no RHP roots.
\(p(S) = S5 + S4 + 6S^3 + 6S^2 + 255 + 25\) has no RHP roots.
The following are the solutions to determine RHP roots in the given polynomials in Control System:
Polynomial: \(p(S) = S5 + S4 + 25^3 + 35^2 + S + 4\)
To identify the number of RHP (Right Half Plane) roots of the given polynomial \(p(S) = S5 + S4 + 25^3 + 35^2 + S + 4\), the number of sign changes in the coefficients of the polynomial's terms can be counted.
Using the Descartes rule of sign, the number of sign changes in the polynomial's coefficients will indicate the number of positive or RHP roots present in the polynomial.
Therefore, there is no change in the sign of coefficients in the polynomial p(S).Thus, the number of RHP roots of the polynomial \(p(S) = S5 + S4 + 25^3 + 35^2 + S + 4\)is zero.
Polynomial: \(p(S) = S5 + S4 + 6S^3 + 6S^2 + 255 + 25\)
The given polynomial is \(p(S) = S5 + S4 + 6S^3 + 6S^2 + 255 + 25\).
The coefficients of the polynomial are as follows:
a5 = 1, a4 = 1, a3 = 6, a2 = 6, a1 = 1, and a0 = 25.
According to the Routh-Hurwitz criterion, the RHP roots of the polynomial p(S) are given by the following conditions:
For the polynomial \(p(S) = S5 + S4 + 6S^3 + 6S^2 + 255 + 25\), the Routh array can be written as:
1 6 25 0
1 6 25 0
6 155 0
5 25 0
25 0
Thus, the polynomial p(S) has no RHP roots since the Routh array contains no changes of sign.
Therefore, the given polynomial has no RHP roots.
Hence, the solutions for the given problem are as follows:
\(p(S) = S5 + S4 + 25^3 + 35^2 + S + 4\) has no RHP roots.
\(p(S) = S5 + S4 + 6S^3 + 6S^2 + 255 + 25\) has no RHP roots.
To know more about RHP roots, visit:
https://brainly.com/question/15234445
#SPJ11
Write an equation of the line that passes
through (0, – 5) and is perpendicular to
the line y= - 4/5x
Answers
Answer:
\(y = \frac{5}{4} x - 5\)
the tangent function is periodic because it repeats at regular intervals what is the period of the tangent function?
Answers
The tangent function is periodic and the period of the tangent function is π.
Since y=tan x is a many-one function and tan x has a periodic function with period π, the graph of the tangent function repeats itself at regular intervals of length units.
Because the tangent function is an odd function and the graph of y=tan x is symmetric about the origin.
Since its range is from -∞ to ∞, the tangent function is an unbounded function.
In a complete circular rotation, it make Two cycles. In the factors of π, it repeats its interval. Example, π, 2π, 3π.
The period of the tangent function is π.
To learn more tangent function on here:
https://brainly.com/question/22161213#
#SPJ4
(b) what is the (approximate) probability that the sample mean hardness for a random sample of 35 pins is at least 51?
Answers
To solve this problem, we need to use the Central Limit Theorem, which states that the distribution of the sample means approaches a normal distribution as the sample size increases.
First, we need to find the mean and standard deviation of the sample mean hardness. The mean is simply the population mean, which is given as 50.5. The standard deviation of the sample mean is given by the formula:
standard deviation of sample mean = population standard deviation / sqrt(sample size)
The population standard deviation is given as 0.5, and the sample size is 35, so:
standard deviation of sample mean = 0.5 / sqrt(35) = 0.084
Next, we need to standardize the sample mean hardness using the z-score formula:
z = (sample mean hardness - population mean) / (standard deviation of sample mean)
z = (51 - 50.5) / 0.084 = 5.95
Finally, we need to find the probability that a standard normal distribution is greater than or equal to 5.95. This can be done using a z-table or a calculator. Using a calculator, we get:
P(Z ≥ 5.95) ≈ 0
Therefore, the approximate probability that the sample mean hardness for a random sample of 35 pins is at least 51 is very close to 0.
To learn more about mean : brainly.com/question/31101410
#SPJ11
the unit price f ingredients a and b used in a solution increased by 10% and 25% respectively. if ingredients a and b are used in ratio of 2:1 respectively, what is the overall percentage increase in price?
Answers
The overall percentage increase in price is 1.5, which means that the price of the solution has increased by 150%. This means that if the original price of the solution was $300, the new price after the increase would be $750.To find the overall percentage increase in price, we need to use the ratio of ingredients a and b, which is 2:1.
This means that for every 2 units of ingredient a used, 1 unit of ingredient b is used.
Let's assume that the original unit price of ingredient a was $100 and the original unit price of ingredient b was $200. After the increase, the unit price of ingredient a would be $110 (10% increase) and the unit price of ingredient b would be $250 (25% increase).
To find the overall percentage increase in price, we need to calculate the weighted average of the two ingredients based on their ratios. This can be done by multiplying the percentage increase in each ingredient by its weight in the ratio and adding them together.
The weighted average percentage increase in price can be calculated as follows:
[(2/3) x 10%] + [(1/3) x 25%] = (20/30) + (25/30) = 45/30 = 1.5
Therefore, the overall percentage increase in price is 1.5, which means that the price of the solution has increased by 150%. This means that if the original price of the solution was $300, the new price after the increase would be $750.
learn more about percentages here: brainly.com/question/29142213
#SPJ11
