What is the slope of the line that passes through the points (5, 1) and (2, -7)?
Answers
So you get -6/-3, which equals 2
SLOPE IS 2
Answer:
m [ slope ] = 8/3
Step-by-step explanation:
What is the slope of the line that passes through the points (5, 1) and (2, -7)?
m = ∆y / ∆x
m = y₂ – y₁ / x₂ – x₁
| (5, 1) → (x₁, y₁) | (2, -7) → (x₂, y₂) |
[each coordinate will correspond (directly go to) to the variables shown]
m = (-7) – (1) / (2) – (5)
m = -8 / -3
m = 8 / 3
This means that this line has a rise of 8 and a run of 3.
Up 8 and right 3 proportionally, it would touch the opposite corners of a plane that was 8 by 3 units.
Slope can be thought of as the steepness of a line, the greater the slope, the greater the steepness.
These points are generally known as cartesian coordinates.
____________
Once you have the slope, you can back track from one of the coordinates to find the equation of the line.
Just multiply the slope by the x of either coordinate, make it opposite, and then add that to the y of that coordinate to get b [the y-intercept; where it crosses the y axis, x is always 0]
Since (2, -7) is closer to the y axis than (5, 1) it is more convenient.
In (2, -7), 2 is the x variable and -7 is the y variable.
-mx + y = (-8/3)(2) + (-7) = -16/3 + (-21/3)
21/3 is the same as 7 [so it will have a common denominator].
-16 + -21 / 3 = -37/3 = b
Thus this line has an equation of
y = mx + b
↓ ↓
y = 8/3x – 37/3.
__________________________
Or you can refer to point slope which is what is taught:
y – y₁ = m(x – x₁).
You can tell that there are some similarities to this and the slope formula.
m = ( y₂ – y₁ / x₂ – x₁ ) →
m × ( x₂ – x₁ ) =
( y₂ – y₁ / x₂ – x₁ ) × ( x₂ – x₁ )
[multiply the denominator by both sides]
m ( x₂ – x₁ ) = y₂ – y₁
[x₂, and y₂ can just be x and y since you only need the initial coordinate and slope, because the second coordinate can be anything along that line]
m ( x – x₁ ) = y – y₁ →
y – y₁ = m(x – x₁)
[symmetric property of equality]
if a = b, b = a.
Related Questions
School ends at 3:15 pm. The school provides after -school care for a maximum of 150 minutes after school ends. When is the latest time for pick up?
Answers
The latest time for pickup, found by converting the 150 minutes maximum time provided by the school, from minutes to hours is about 5:45 pm
How can minutes be converted into hours?Minutes can be converted into hours by dividing the number of minutes by 60, which is the number of minutes in an hour.
The time that school ends = 3:15 pm
The latest time for pick up after school care = 150 minutes after school ends
Therefore, the latest time for pick up after school care = 3:15 pm + 150 minutes
60 minutes = 1 hour
150 minutes = (1/60) × 150 = 2.5
The latest for pick up = 3:15 pm + 2.5 hours = 5:45 pm
Learn more on unit conversion here: https://brainly.com/question/14614674
#SPJ4
Solve the equation v² = 36. What’s the value of v?
Answers
Answer:
6
Step-by-step explanation:
6 x 6 = 36
Which of the following equations models exponential decay? Select all that apply.

Answers
Answer:
A & D
Step-by-step explanation:
Exponential decay is where the b value (usually the value in parentheses) is less than 1. Anything where that value is less than 1 is decay.
Suppose random variables X and Y are related as Y=7.00X+8.34. Suppose the random variable X has mean zero and variance 1. What is the expected value of Y^2
Answers
Given the relationship between the random variables X and Y, Y = 7.00X + 8.34, and the properties of X (mean of zero and variance of 1), the expected value of Y^2 is 118.5556.
We can find the expected value of Y^2.
First, let's find the mean (expected value) of Y. Since the mean of X is zero, E(Y) = 7.00 * E(X) + 8.34 = 7.00 * 0 + 8.34 = 8.34.
Next, let's find the variance of Y. The variance of Y, Var(Y), can be determined by the relationship Var(Y) = a^2 * Var(X), where a is the coefficient of X (in this case, 7.00). So, Var(Y) = 7.00^2 * 1 = 49.
Now, we can find the expected value of Y^2 using the formula E(Y^2) = Var(Y) + E(Y)^2. Plugging in the values, E(Y^2) = 49 + 8.34^2 = 49 + 69.5556 = 118.5556.
Therefore, the expected value of Y^2 is 118.5556.
To know more about Variance visit:
https://brainly.com/question/14116780
#SPJ11
Please help.
Is algebra.

Answers
m is the gradient.
To find the gradient the formula is;
Rise/Run
3/-3
= -1
x is the x intercept
-2.5
c is the y intercept
3
y = mx + c
y = -1(-2.5) + 3
y = 2.5 + 3
y = 5.5
-15 + 6x - 19 - 20%
Simplify by combining like terms. I’m so confused please help!!
Answers
Answer:
6x-34-20%
(please give brainliest, it really helps a lot!)
You need to just focus on the units, (I believe that the percentage was just meants to throw you off)
Can someone please help me with this ty!!

Answers
Answer:
3x - 8
Step-by-step explanation:
The equation in slope-intercept form is y = 3x - 8
Slope intercept form is y = mx + b.
The m is the slope, which you can calculate using any two points from the table. Or use the table to observe the pattern "x increase by 1" and " y increase by 3". Slope is the change in y over the change in x. Here the change in y is 3. And change in x is 1. So slope is 3/1, which is just 3.
The b in the
y = mx + b is the y-intercept, where the graph crosses the y-axis. The point on the table is (0,-8) So in this case the b is -8.
So we fill in these numbers m=3, b=-8 into y=mx+b and get the answer.
y = 3x - 8
Plz help
Find ‘x’ & ‘y’

Answers
Answer:
x=20. y=15
Step-by-step explanation:
in similar triangles the sides are all in proportion. this means:
\( \frac{25}{5} = \frac{x}{4} = \frac{y}{3} \)
\( \frac{25}{5} = 5\)
so:
\( \frac{x}{4} = 5\)
x=5×4
x=20
and...
\( \frac{y}{3} = 5\)
y=3×5
y=15
A certain forest covers an area of 4800 km^2 . Suppose that each year this area decreases by 5.25% . What will the area be after 6 years? Use the calculator provided and round your answer to the nearest square kilometer.
Answers
Answer:
the area after 6 years is 3,473 km^2
Step-by-step explanation:
The computation of the area after 6 years is as follows:
= Area × (1 - decreased percentage)^number of years
= 4,800 km^2 × (1 - 5.25%)^6
= 4,800 km^2 × 0.9475^6
= 3,473 km^2
Hence, the area after 6 years is 3,473 km^2
In the diagram below, KJ is congruent to LJ. If m of angle J = 98° and m of angle K = 11x+8, determine the value of x.

Answers
1. Use the given information KJ is congruent to LJ:
Given line segment KJ and line segment LJ are congruent you know their opposite side angles are also congruent
2. Find the angle measures:
Given that J= 98 you know angle K+L equals to 180-89, this is because they are congruent therefore they must equal what is left. After you divide by 2 to split the remaining amount evenly which states angle K = 41 and angle L = 41
3. Set up the equation:
Knowing angle K is 41 and given that it’s also 11x+8 you set up the following algebraic equation: 11x+8=41
4. Solve for x:
11x+8=41 | subtract 8 from both sides
11x=33 | divide by 11
X=3
Which of the following are valid vector products: A. c
A
=(cA
x
,cA
y
,cA
z
) B.
A
⋅
B
=(A
x
B
x
,A
y
B
y
,A
z
B
z
) C.
A
×
B
=(A
y
B
z
−A
z
B
y
,A
z
B
x
−A
x
B
z
,A
x
B
y
−A
y
B
x
) D.
A
⋅
B
=∣
A
∣∣
B
∣Cos(θ) E. ∣
A
×
B
∣=∣
A
∣∣
B
∣∣Sin(θ)∣ E B A D C
Answers
The question asks which of the given options are valid vector products. The options include different vector operations involving vectors A and B, such as scalar multiplication, dot The question asks which of the given options are valid vector products. The options include different vector operations involving vectors A and B, such as scalar multiplication, dot product, cross product, and magnitude calculations.
Among the given options, the valid vector products are C and E.
Option C represents the cross product of vectors A and B, which is a valid vector product. The cross product of two vectors results in a new vector that is orthogonal (perpendicular) to both vectors.
Option E represents the magnitude of the cross product of vectors A and B, which is also a valid vector product. The magnitude of the cross product represents the area of the parallelogram formed by the two vectors and is equal to the product of their magnitudes multiplied by the sine of the angle between them.
The other options, A, B, and D, do not represent valid vector products. Option A represents scalar multiplication of vector A by a scalar c, which results in a scaled version of vector A but not a new vector product. Option B represents component-wise multiplication, not a valid vector product. Option D represents the dot product, which results in a scalar value, not a vector product.
In summary, the valid vector products among the given options are C and E, representing the cross product and magnitude of the cross product, respectively.
Learn more about vector:
https://brainly.com/question/30958460
#SPJ11
Tara owns a pizza shop. The item purchased most frequently from her shop is a large
pizza. For any order, Tara charges $7.00 for each pizza plus $3.00 for delivery services.
Tara made a delivery of pizzas to a party for which she charged $45.00. How many
pizzas did she deliver?
Only an algebraic solution will be accepted.
answer in an algebraic solution
Answers
Answer:
p = 6
Step-by-step explanation:
p = the number of pizzas$7.00 × p + 3 = 45
Simplify to:
7p + 3 = 45
- 3 - 3
7p = 42
÷7 ÷7
p = 6
Find the critical numbers of the function. f(x)=3x4+8x3−48x2
Answers
The critical numbers of the function f(x) = \(3x^4 + 8x^3 - 48x^2\) are x = -2, x = 0, and x = 4.
To find the critical numbers of a function, we need to find the values of x where the derivative of the function is either zero or undefined.
Let's start by finding the derivative of the function f(x) = \(3x^4 + 8x^3 - 48x^2\). Taking the derivative with respect to x, we get:
f'(x) = \(12x^3 + 24x^2 - 96x\)
Now, to find the critical numbers, we set the derivative equal to zero and solve for x:
\(12x^3 + 24x^2 - 96x = 0\)
Factoring out 12x, we have:
\(12x(x^2 + 2x - 8) = 0\)
Now, we can solve for x by setting each factor equal to zero:
12x = 0 ---> x = 0
\(x^2 + 2x - 8 = 0\)
Using the quadratic formula, we find the roots of the quadratic equation:
x = (-2 ±\(\sqrt{ (2^2 - 4(1)(-8))}\)) / (2(1))
= \((-2 ± sqrt(36)) / 2\)
= (-2 ± 6) / 2
Simplifying, we have:
x = -2 + 6 = 4
x = -2 - 6 = -8
However, since we are looking for the critical numbers within a specific domain, we discard x = -8 as it is outside the domain.
Therefore, the critical numbers of the function are x = -2, x = 0, and x = 4.
To learn more about function, click here: brainly.com/question/11624077
#SPJ11
1250392 nearest thousand please answer me
Answers
Answer: 1,250,000
Step-by-step explanation:
What is the measure of angle S? A. 27° B. 58° C. 95° D. 180°
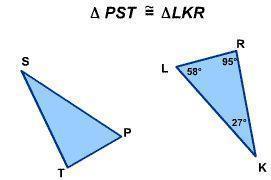
Answers
Answer:
A. 27°
Step-by-step explanation:
triangle PST is congruent to triangle LKR
<S corresponds to <K.
m<S = m<K = 27°
Step-by-step explanation:
angle tsp=angle rkp=27°
angle S=360-27°
angle S=333°
Please mark me as brainliest
Emily waited in line for the StarCraft video game for 3 hours. If the line was only moving 2 1⁄4 feet per hour, how far did Emily move in the line?
Answers
Answer:
6 3/4 feet
Step-by-step explanation:
Answer:
6 3/4 feet
Step-by-step explanation:
2 1/4 x 3 = 6 3/4
Hanz’s class had a goal to collect 250 cans of food for the school food drive. They collected 290 cans. What percent of their goal did they achieve?
Answers
Given:
Goal = 250 cans
Number of collected cans = 290
To find:
The percent of their goal they achieved.
Solution:
The percent of their goal they achieved is:
\(\text{Required percent}=\dfrac{\text{Number of collected cans}}{\text{Goal}}\times 100\)
\(\text{Required percent}=\dfrac{290}{250}\times 100\)
\(\text{Required percent}=\dfrac{29}{25}\times 100\)
\(\text{Required percent}=29\times 4\)
\(\text{Required percent}=116\)
Therefore, they achieved 116% of their goal.
Given a normal distribution with μ=51 and sigma=8, and given you select a sample of n=100, complete parts (a) through(d).
a. What is the probability that X is less than 49? P(X= 0.00620.0062
b. What is the probability X is between 49 and 50.5?P(49< X < 50.5)
Answers
These probabilities are obtained by standardizing the values using the formula z = (x - μ) / σ, where x is the given value, μ is the mean, and σ is the standard deviation.
(a) The probability that X is less than 49 in a normal distribution with μ=51 and σ=8 is approximately 0.0062, or 0.62%.
(b) The probability that X is between 49 and 50.5 in the same normal distribution is approximately 0.1499, or 14.99%.
(a) To find the probability that X is less than 49 in a normal distribution with μ=51 and σ=8, we need to calculate the cumulative probability using the standard normal distribution table or a calculator. Using either method, we find that the probability is approximately 0.0062, or 0.62%.
(b) Similarly, to find the probability that X is between 49 and 50.5, we calculate the difference between the cumulative probabilities of 50.5 and 49. Using the standard normal distribution table or a calculator, we find that the probability is approximately 0.1499, or 14.99%.
These probabilities are obtained by standardizing the values using the formula z = (x - μ) / σ, where x is the given value, μ is the mean, and σ is the standard deviation. By looking up the standardized values in the standard normal distribution table, we can determine the corresponding probabilities.
Learn more about probabilities here: brainly.com/question/29381779
#SPJ11
density of 222.50 g and 25.00 cm3
Answers
Answer:
8.9 grams per centimeters cubed
Step-by-step explanation:
The formula for density is D=M÷V
Just divide 222.50 by 25.00 and you are done.
Area and Length of Sectors of Circles
I want
serve
cookie саке
at my
party.
Each cookie cake is 8 inches long. Fill in the chart below with the missing information
then calculate how many cookie cakes I should buy.
Answers
The missing information are,
Person Percentage Fractional Central angle Amount Amount of
amount of cookies frosting
Cousin 50% 1/2 180° 25.15 in² 12.55 in²
Jacob
Sister1 25% 1/4 90° 12.58 in² 6.275 in²
Uncle 75% 3/4 270° 37.73 in² 18.83 in²
Aunt 10% 1/10 36° 5.03 in² 2.51 in²
What is mean by Angle?An angle is a combination of two rays (half-lines) with a common endpoint. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle.
Given that;
I want serve cookie саке at my party.
And, Each cookie cake is 8 inches long.
Hence, The missing information are,
Person Percentage Fractional Central angle Amount Amount of
amount of cookies frosting
Cousin 50% 1/2 180° 25.15 in² 12.55 in²
Jacob
Sister1 25% 1/4 90° 12.58 in² 6.275 in²
Uncle 75% 3/4 270° 37.73 in² 18.83 in²
Aunt 10% 1/10 36° 5.03 in² 2.51 in²
Learn more about the angle visit:;
https://brainly.com/question/25716982
#SPJ9

for what values of a are the following expressions true 1/2a-5 1/2=5-a
Answers
The expression is only true for a = 5.
What is the expressions?An expression is a combination of numbers, variables, and operations that represents a quantity or a mathematical relationship. It can be a simple or complex representation of a value or function, and it can be evaluated or simplified using algebraic or numerical methods.
The given expression is:
(1/2)a - 5 (1/2) = (5 - a)
To find the values of 'a' that make this expression true, we can simplify and solve the equation:
(1/2)a - 2.5 = 5 - a
Adding 'a' to both sides:
(3/2)a - 2.5 = 5
Adding 2.5 to both sides:
(3/2)a = 7.5
Multiplying both sides by 2/3:
a = 5
Therefore, the expression is true when a = 5.
To verify, we can substitute a = 5 into the original expression:
(1/2)(5) - 5 (1/2) = (5 - 5)
2.5 - 2.5 = 0
The expression evaluates to 0, which is true.
Therefore, the expression is only true for a = 5.
To know more about expression, visit:
https://brainly.com/question/1859113
#SPJ1
Determine whether or not each indicated set of 3x3 matrices isa subspace of M33.
The set of all symmetric 3x3 matrices (that is, matricesA=[aij] such that aij = aji for1<= i <= 3, 1<=jj<=3.)
Answers
The set of all symmetric 3x3 matrices satisfies all three conditions for a subspace, it is indeed a subspace of M33
To determine whether the set of all symmetric 3x3 matrices is a subspace of M33, we need to check if it satisfies the three conditions for a subspace:
Closure under addition: If A and B are both symmetric 3x3 matrices, then A+B will also be a symmetric 3x3 matrix since \((A+B)^T = A^T + B^T = A + B\). Therefore, the set is closed under addition.
Closure under scalar multiplication: If A is a symmetric 3x3 matrix and c is a scalar, then cA will also be a symmetric 3x3 matrix since \((cA)^T = cA^T = cA\). Therefore, the set is closed under scalar multiplication.
Contains the zero vector: The zero vector in M33 is the matrix of all zeroes. This matrix is also a symmetric 3x3 matrix since all its entries are equal. Therefore, the set contains the zero vector.
Since the set of all symmetric 3x3 matrices satisfies all three conditions for a subspace, it is indeed a subspace of M33.
For more such questions on matrices
https://brainly.com/question/27929071
#SPJ11
For the position function s(t) = 3t2 - 2t + 1, where "t" is measured in minutes and "s(t)" is measured in feet, use the Limit Definition of the Derivative to find each of the following (and be sure to include appropriate units in your final answers):a) Velocity, which is s'(t). b) Acceleration, which is dt2
Answers
The velocity function is s'(t) = 6t - 2, and the units are feet per minute. The acceleration function is s''(t) = 6, and the units are feet per minute squared.
a) To find the velocity, which is the derivative of the position function with respect to time, we need to use the limit definition of the derivative:
s'(t) = lim(h→0) [s(t+h) - s(t)] / h
= lim(h→0) [(3(t+h)2 - 2(t+h) + 1) - (3t2 - 2t + 1)] / h
= lim(h→0) [3t2 + 6th + 3h2 - 2t - 2h + 1 - 3t2 + 2t - 1] / h
= lim(h→0) [6th + 3h2 - 2h] / h
= lim(h→0) [6t + 3h - 2]
= 6t - 2
b) To find the acceleration, which is the derivative of the velocity function with respect to time, we need to take the derivative of the velocity function:
s''(t) = d/dt [6t - 2]
= 6
Learn more about derivative here: brainly.com/question/23819325
#SPJ4
the trapezium is down on a centimetre grid find the area of the trapezium

Answers
Answer:
21 square cm
Step-by-step explanation:
\( b_1 = 9 \:cm, \: b_2 = 5 \:cm, \: h = 3\: cm\\
Area\: of\: trapezium\\
= \frac{1}{2} (b_1 +b_2)\times h\\\\
= \frac{1}{2} (9 +5)\times 3\\\\
= \frac{1}{2} \times 14 \times 3\\\\
= 7 \times 3\\\\
= 21 \: cm^2 \)
b = 21 feet h = 16 feet Find the area of the triangle. 168 sq. feet 85 sq. feet 100 sq. feet 108 sq. feet
Answers
Answer:
168 sq
Np also you could've just searched it up
let f(x)=4^x. The new function g(x)=f(x-1)+3 represents transformations that were made to function f. Type the new equation for g. g(x)=___
Describe the two types of transformations that occur between function f and function g. (use words like up, down, left, right, compression or stretch in your answer.)

Answers
Answer:
g(x) = \(4^{(x-1)}+3\)
Step-by-step explanation:
Given exponential function is,
f(x) = \(4^{x}\)
If the given function is shifted 1 unit to the right,
h(x) = f(x - 1)
= \(4^{(x-1)}\)
If the function 'h' is shifted 3 units up,
g(x) = h(x) + 3
= \(4^{(x-1)}+3\)
Therefore, transformed function will be,
g(x) = \(4^{(x-1)}+3\)
PLEASE EXPLAIN AND SHOW YOUR WORK THANK YOU!!
Solve as a MIXED NUMBER:
-2.25 + 0.4x = -2.8
THANK YOU!
Answers
Answer:
-1 3/8
Step-by-step explanation:
-2.25 + 0.4x = -2.8
-2.25 + 2.25 + 0.4x = -2.8 + 2.25 ==> add 2.25 on both sides to isolate x
0.4x = -0.55
(0.4x = -0.55)*20 ==> multiply the equation by 20 to remove decimals
8x = -11
x=-11/8
x=-(3+8)/8 ==> turn x into a mixed number
x=-3/8 - 8/8
x=-3/8 - 1 ==> simplify
x=-1 - 3/8
x=-(1 + 3/8)
x=-1 3/8
how many cubes, with side measures of 2 cm, will fit inside a right rectangular prism with dimensions of 6 cm by 8 cm by 4 1 2 cm? group of answer choices 24 108 54 27
Answers
Answer:
Using the volume formula we know that (B) 27 cubes can be fitted into the right rectangular prism.
What is the right rectangular prism?
The right rectangular prism has four rectangle-shaped side faces and two parallel end faces that are perpendicular to each of the bases.
Parallelograms make up the sides of an oblique prism, a non-right rectangular prism.
A cuboid is yet another name for a right rectangle prism.
So, the volume of the right rectangular prism:
V = wlh
Insert values:
V = wlh
V = 6*8*4.5
V = 216cm³
Now, the volume of the cube:
V = a³
V = 2³
V = 8cm³
Then, the number of cubes that can be fitted in the right rectangular prism:
216/8 = 27
Therefore, using the volume formula we know that (B) 27 cubes can be fitted into the right rectangular prism.
Know more about the right rectangular prism? here:
brainly.com/question/3317747
#SPJ1
Correct question:
How many cubes, with side measures of 2 cm, will fit inside a right rectangular prism with dimensions of 6 cm by 8 cm by 4 1/2 cm?
Group of answer choices
a. 24
b. 27
c. 108
d. 54
The final answer is 27
To determine how many cubes will fit inside the right rectangular prism, we need to find the volume of the prism and the volume of the cubes, then divide the volume of the prism by the volume of the cubes.
Volume of a cube (V_cube) = side^3
V_cube = 2 cm * 2 cm * 2 cm = 8 cubic cm
Volume of the right rectangular prism (V_prism) = length * width * height
V_prism = 6 cm * 8 cm * 4.5 cm = 216 cubic cm
Now, divide the volume of the prism by the volume of the cubes:
Number of cubes = V_prism / V_cube = 216 cubic cm / 8 cubic cm = 27 cubes
Therefore, 27 cubes with side measures of 2 cm will fit inside the right rectangular prism.
To know more about cubes visit : https://brainly.com/question/28134860
#SPJ11
Given E(-6, y), F(6, 5), G(14, 11), and
H(8,-13), find the value of y so that
EF is perpendicular to GH.
Answers
the answer is y = 16.
What is slope?In mathematics, the slope or gradient of a line is a number that describes both the direction and the steepness of the line.
here, we have,
E(-6, y), F(6, 5), G(14, 11), and H(8,-13),
& EF is perpendicular to GH.
now, we get,
The slope of GH is ...
G -H = (14, 11) -(8, -13) = (6, 24) = (Δx, Δy)
slope = Δy/Δx = 24/6 = 4
The perpendicular line through F will have a slope of the negative reciprocal of this, or -1/4.
The point-slope form of the equation can be written as ...
y -k = m(x -h) . . . . . line with slope m through point (h, k)
The perpendicular line through F is then ...
y -13 = (-1/4)(x -6)
For an x-value of -6, the value of y will be ...
y = (-1/4)(-6 -6) +13 = 12/4 +13 = 16
hence, The value of y so that EF is perpendicular to GH is 16.
To learn more on slope click:
brainly.com/question/3605446
#SPJ5
Answer the circle question please.

Answers
\(\frac{11}{-6}\)