Brainliest for the first correct answer! Which scenario is modeled in the diagram below? (look at attached image)
A) Kaia saved $55.15 on a new guitar because it was 75 percent off. She paid $220.60 for the guitar.
B) Kaia saved $165.45 on a new guitar because it was 75 percent off. She paid $220.60 for the guitar.
C) Kaia saved $55.15 on a new guitar because it was 75 percent off. The price of the guitar before the discount was $220.60.
D) Kaia saved $165.45 on a new guitar because it was 75 percent off. The price of the guitar before the discount was $220.60.
This was on edge

Answers
Answer:
D) Kaia saved $165.45 on a new guitar because it was 75 percent off. The price of the guitar before the discount was $220.60.
Step-by-step explanation:
Given in the attached diagram shows a model of a discount given on a purchase of guitar showing 75% of the price of guitar ($55.15 + $55.15 + $55.15) that was given.
It also tells that the price pays is 25% of the price of the guitar before the discount. I.e. 25% of %220.60 = 0.25 × 220.60 = $55.15.
From the diagram given, we can infer that Kaia bought the guitar at $55.15 while saving $165.45. That is 25% of the original price. And the amount saved, $165.45, is %75 of the original price ($55.15+$55.15+$55.15).
The answer is D.
Answer:
Kaia saved $165.45 on a new guitar because it was 75 percent off. The price of the guitar before the discount was $220.60.
or D
Step-by-step explanation:
i got it right on my test
if you can please mark as branliest
Related Questions
Given: tangent to Circle O.
If m = 140°, then A =
Answers
The measure of the angle A is 70 degrees if the DR is the tangent to the circle option (A) 70 degrees is correct.
What is a circle?It is described as a set of points, where each point is at the same distance from a fixed point (called the center of a circle)
The question is incomplete.
The complete question is in the picture, please refer to the attached picture.
It is given that:
Join the points B and O and then join points D and O
Angle A = (1/2)Angle BOD
Angle B = 140 degrees
Angle A = (1/2)140 degrees
Angle A = 70 degrees
Thus, the measure of the angle A is 70 degrees if the DR is the tangent to the circle option (A) 70 degrees is correct.
Learn more about circle here:
brainly.com/question/11833983
#SPJ1

Which of the following has the same absolute value as 5? a. .5 b. 1/2 c. 1/5 d. -5
Answers
Answer:
D..-5
Step-by-step explanation:
absolute value is the "opposite" of the number or the same amount of "steps" from 0 on the opposite side.
Find the inverse of the function below. When typing your answer use the "^" key (shift+6) to indicate an exponent. For example, if we have x squared (x times x) we would type x^2.()=9+4−4‾‾‾‾‾‾√f(x)=9+4x−4The numerator of −1()f−1(x) is Answer -Answer +Answer The denominator of −1()f−1(x) is Answer

Answers
Given:
There are given that the function to find the inverse is:
\(f(x)=9+\sqrt[]{4x-4}\)Explanation:
To find the inverse of the given function, first, we need to exchange f(x) into y, then exchange the variable which means change y to x and x to. Then, find the value of y.
Now,
Step 1:
Exchange f(x) into y:
\(\begin{gathered} f(x)=9+\sqrt[]{4x-4} \\ y=9+\sqrt[]{4x-4} \end{gathered}\)Step 2:
Exchange the variables which means exchange y into x and x into y:
\(\begin{gathered} y=9+\sqrt[]{4x-4} \\ x=9+\sqrt[]{4y-4} \end{gathered}\)Step 3:
Solve the above function for the value of y:
So,
\(\begin{gathered} x=9+\sqrt[]{4y-4} \\ x=9+2\sqrt[]{(y-1)} \\ 2\sqrt[]{(y-1)}=x-9 \\ \sqrt[]{(y-1)}=\frac{x-9}{2} \end{gathered}\)Then,
\(\begin{gathered} \sqrt[]{(y-1)}=\frac{x-9}{2} \\ (y-1)^{\frac{1}{2}}=\frac{x-9}{2} \\ y-1=(\frac{x-9}{2})^2 \\ y=(\frac{x-9}{2})^2+1 \end{gathered}\)Then,
\(\begin{gathered} y=(\frac{x-9}{2})^2+1 \\ y=\frac{x^2-18x+81}{4}^{}+1 \\ y=\frac{x^2-18x+81+4}{4} \\ f^{-1}(x)=\frac{x^2-18x+85}{4} \end{gathered}\)Final answer:
Hence, the numerator of the inverse function and the denominator of the inverse function are shown below:
\(\begin{gathered} \text{The numerator of f}^{-1}(x)\text{ = }x^2-18x+85 \\ \text{The denominator of f}^{-1}(x)\text{ = 4} \end{gathered}\)passes through :(3, -1) Slope: -1/2
write in slope intercept form of a line
Answers
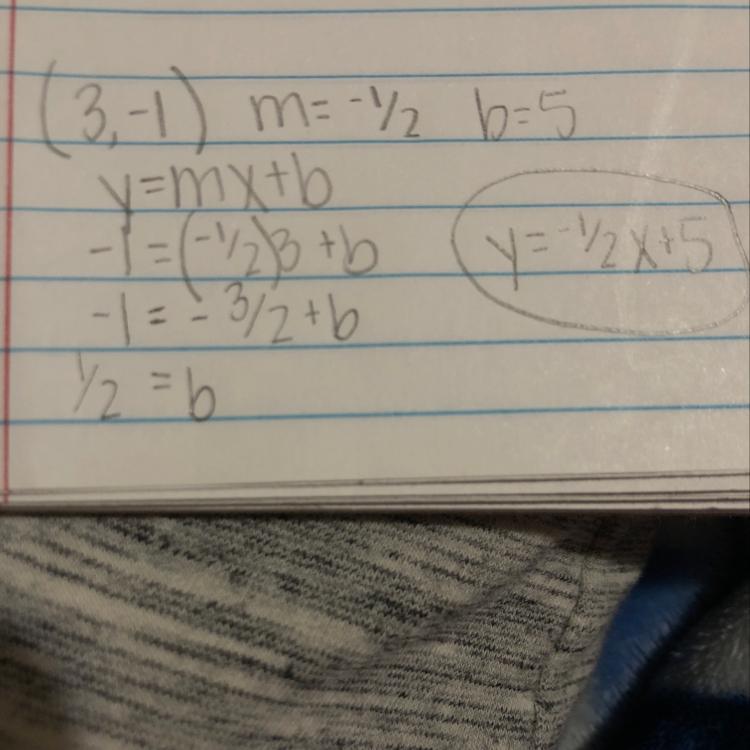
Find the magnitude and direction (in degrees) of the vector. (Assume 0° ≤ < 360°.)
= 6i + 2sqrt3j
Answers
\(6i~~ + ~~2\sqrt{3}j\implies < \stackrel{a}{6}~~,~~\stackrel{b}{2\sqrt{3}} > \\\\[-0.35em] ~\dotfill\\\\ \stackrel{magnitude}{\sqrt{a^2+b^2}}\implies \sqrt{6^2+(2\sqrt{3})^2}\implies \sqrt{36+(2^2\cdot 3)}\implies \sqrt{36+12}\implies \sqrt{48} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{direction}{tan^{-1}\left( \cfrac{b}{a}\right)}\implies tan^{-1}\left( \cfrac{2\sqrt{3}}{6} \right)\implies tan^{-1}\left( \cfrac{\sqrt{3}}{3} \right) \\\\\\ tan^{-1}\left( \cfrac{1}{\sqrt{3}} \right)\implies 30^o\)
Show how to get answer to 493 km 43m + 17km 57m
Answers
The sum of the two distance is 510km 100m.
Here it is given two distances 493km 43m and 17km 57m.
As we know we can divide, multiply, add or subtract only with the same unit.
Here we have to find the sum of the distance,
493 km 43m + 17km 57m
=( 493 + 17)km (43 + 57)m
=510km 100m
Therefore the sum of the distance is 510km 100m.
To know more about the distance refer to the link given below:
https://brainly.com/question/17273444
#SPJ9
Seven years ago, Grogg's dad was 6 times as old as Grogg, and 3 years ago, his dad was 4 times as old as Grogg. How old is Grogg's dad currently?
Answers
Answer:
Grogg's dad is 22
Step-by-step explanation:
Let D = dad's current age
Let g = Grogg's current age
6(d - 7) = g - 7 → 6d - 42 = g - 7 → 6d -35 = g
4(d - 3) = g - 3 → 4d -12 = g - 3 → 4d -9 = g
Set the two equations equal to each other and solve for d
6d - 35 = 4d - 9 Subtract 4d from both sides
2d -35 = -9 Add 35 to both sides
2d = 44 Divide both sides by 2
d = 22
Helping in the name of Jesus.
Answer:
Step-by-step explanation:
d = current dad age
g = current grogg age
d-7 = 6(g-7)
d-3 = 4(g-3)
Let's solve the first equation first:
Add 7 to both sides: d - 7 +7 = 6g - 42 + 7 so d = 6g - 35
Substitude d = 6g - 35 for d in d - 3 = 4g - 12
(6g-35)-3 = 4g-12 = 6g-38 = 4g-12
Subtract 4g from both sides: 2g - 38 = -12
Add 38 to both sides: 2g = 26
Easy: g = 13
And now substitude g in for any equations.
d-3 = 52-12
d = 43
The group defined by the following table is called the group of quaternions. Use the table to determine each of the following. a. The center
Answers
Step 1 of 5
(a) Recall the definition, Center of a Group,
“The center, , of a group is the subset of elements in that commute with every element of . In symbols,
”.
Since
for every , we obtain .
Since
, we obtain
It takes 9 1/2 inches of string to make one bracelet. How many bracelets can be made if you only have 5 yards of string?
Answers
Answer:
18
Step-by-step explanation:
Find the value of x

Answers
The 2 angles total 120
The 2x angle is 120 - 70 = 50 degrees.
2x = 50
Divide both sides by 2:
x - 25
Answer:
\(2x + 70 = 120 \\2x = 120 - 70 \\ 2x = 50 \\ x = \frac{50}{2} \\ \boxed{x = 25}\)
25° is the right answer.22) Original price of shorts: $19.9 Tax: 2%
Answers
Answer:
$20.298, round to $20.30
Step-by-step explanation:
The orginal price of the shorts are $19.90, and the tax is 0.02 (2%), so you multiple 19.90*0.02, which is $0.398, and then you add it to $19.90 to get $20.298.
Answer:
$0.39 cents
Step-by-step explanation:
2% of 19.9 is 0.398 but we will just say 39 cents :)
The perimeter of a rectangle is 90 cm the length is 27 cm what is the width of the rectangle
Answers
Answer:
width = 18 cm
Step-by-step explanation:
perimeter of rectangle = 2(length + width)
then:
90 = 2(27+w)
90/2 = 27+w
w = width
45 = 27+w
45 - 27 = w
18 = w
Check:
90 = 2(27+18)
90 =2*45 =
0.5 (-2 + 4d) -13 for d
Answers
Step-by-step explanation:
-13 x 4 = -52
-52 x 0.5 = -25
-2 x 0.5 = -1
-1 + -25 = -26
Question 13
Which expression is equivalent to 45x - 15x? Choose all that apply.
A
30
B.
30x
с
60x
D
x(45-15)
Answers
Answer:
B. 30x
D. x(45-15)
Step-by-step explanation:
The distributive property lets you factor out the common factor of x. The sum of coefficients can be simplified to a single coefficient.
45x -15x = x(45 -15) = 30x
In a pre algebra class containing 43 students, there are 4 freshman, 35 sophomores, and 4 juniors. what fraction of the class are sophomores
Answers
The fraction of the class that is sophomores is \(35/43\).
The fraction of the class that is sophomores, divide the number of sophomores by the total number of students in the class.
Number of sophomores = 35
Total number of students = 43
Fraction of sophomores = (Number of sophomores)/(Total number of students Fraction of sophomores)
Fraction of sophomores \(= 35 / 43\)
Therefore, the fraction of the class that are sophomores is = \(35/43\).
To learn more about Fraction here,
https://brainly.com/question/10354322
Please Help realy I need it

Answers
Una deuda de $1500 se cancelará a un plazo de 6 trimestres con una tasa del 5% compuesto mensual. Determine:
a) El valor final que termina cancelando por la deuda contraída.
b) Calcule el tiempo (trimestres) que se demora el mismo préstamo inicial tomando como referencia una tasa del 12% anual compuesta.
Answers
a) Una deuda total de $ 4837.65 en un período de amortización debe ser pagada en seis trimestres.
b) Se requiere aproximadamente 42 trimestres para pagar la misma deuda.
¿Cómo determinar el valor final a pagar y el tiempo requerido de amortización?En este problema tenemos dos casos de préstamos bajo un modelo de interés compuesto, léase un caso acumulativo de intereses en el tiempo, en función de períodos definidos. La persona que recibe el préstamo se hace acreedora de una deuda, la cual debe ser amortizada en el tiempo. Ahora, bien, el modelo de interés compuesto se describe bajo la siguiente fórmula:
D' = D · (1 + r / 100)ˣ
Donde:
D - Deuda inicial, en unidades monetarias.D' - Deuda final, en unidades monetarias.r - Tasa de interés, en porcentaje.x - Número de períodos de amortización, en unidades de tiempo.a) Si sabemos que D = 1500, r = 5 y x = 24, entonces:
D' = 1500 · (1 + 5 / 100)²⁴
D' = 4837.65
La persona debe pagar una deuda total de $ 4837.65 en un período de amortización de seis trimestres (nótese que un año tiene cuatro trimestres).
b) Es preciso determinar el período equivalente para una tasa de interés compuesta anual de 12 %, esto es:
D' = D · (1 + r /100)ˣ
㏒ (D' / D) = x · ㏒ (1 + r / 100)
㏒ D' - ㏒ D = x · ㏒ (1 + r / 100)
x = (㏒ D' - ㏒ D) / [㏒ (1 + r / 100)]
x = (㏒ 4837.65 - ㏒ 1500) / [㏒ (1 + 12 / 100)]
x = 10.332 años (aprox. 42 trimestres)
El período de amortización es de aproximadamente 42 trimestres.
Para aprender más sobre interés compuesto: https://brainly.com/question/23137156
#SPJ1
Segments AB, EF, and CD intersect at point C, and angle ACD is a right angle. Find the value of g.

Answers
Answer:
angle g = 37 degrees
Step-by-step explanation:
angle g = 180-90-53 = 37 degrees
NO LINKS!!!
5. Find the domain and range for the graph

Answers
Remember that
For a pair (x,y)
x is domainy is rangeSo
here
Domain:-
[-5,oo)As the function starts from -5 and tends to infinity .
Range:-
[-3,3)As the function starts from -3 but has an asymptote at y=3 .
Answer:
From inspection of the graph, it appears that the curve approaches y = 3 but never crosses it. Therefore, there could be an asymptote at y = 3.
Domain: input values (x-values) → [-5, ∞)
The x-values of the curve start at x = -5 and tends to infinity.
Range: output values (y-values) → [-3, 3)
The y-values of the curve start at y = -3 and appears to tend towards y = 3
The amount of time required to reach a customer service representative has a huge impact on customer satisfaction. Below is the Excel output from a study to see whether there is evidence of a difference in the mean amounts of time required to reach a customer service representative between two hotels. Assume that the population variances in the amount of time for the two hotels are not equal. What is the smallest level of significance at which the null hypothesis will still not be rejected
Answers
Answer:
The smallest level of significance at which the null hypothesis will still not be rejected is 0.05.
Step-by-step explanation:
The \(p-\) value of t-test is \(0.725009\). This \(p-\) value is greater than \(0.05\).
Hence, the null hypothesis is not rejected and conclude that there is no sufficient evidence of a difference in the mean amount of time required to reach a customer service representation between two hotels.
The complete question is :

Sixty men can build a wall in 40days but though they begin the work together, 55 men quit every ten days. The Time needed to build the wall is?
Answers
It would take 370 days to build the wall with the given conditions.
If 60 men can build a wall in 40 days, then the total man-days required to build the wall is:
60 men x 40 days = 2400 man-days
However, 55 men quit every ten days, which means that after 10 days, there are only 60 - 55 = 5 men left to work on the wall. After 20 days, there are only 5 - 55 = -50 men left, which means that the remaining 5 men cannot work any faster than they were already working. Therefore, we can assume that the remaining 5 men complete the wall on their own.
The number of man-days required for the first 10 days is:
60 men x 10 days = 600 man-days
The number of man-days required for the second 10 days is:
5 men x 10 days = 50 man-days
The total number of man-days required for the first 20 days is:
600 man-days + 50 man-days = 650 man-days
The remaining work can be completed by the 5 men in:
2400 man-days - 650 man-days = 1750 man-days
Therefore, the total time needed to build the wall is:
20 days + 1750 man-days / 5 men = 20 + 350 days = 370 days
For such more questions on conditions
https://brainly.com/question/18395678
#SPJ8
Taylor buys bottles of nail polish that cost $3.95 each. She has a maximum of $30 to spend on nail polish purchases. The total cost, with respect to bottles purchased, can be modeled by a function. Which statement correctly defines the domain of the function?
Answers
Answer:
The domain is the set of all whole numbers greater than or equal to 0 and less than or equal to 8
Step-by-step explanation:
Please help me with this.

Answers
The equation of a circle with center at (1, -3) and radius of 3 units is given as (x - 1)² + (y + 3)² = 9
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
The equation of a circle with center at (h, k) and radius of r is given by:
(x - h)² + (y - k)² = r²
The equation of a circle with center at (1, -3) and radius of 3 units is given as:
(x - 1)² + (y + 3)² = 3²
(x - 1)² + (y + 3)² = 9
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
+b4+c4 = 20² (b²+c²), prove
that A:45° or 135°
Answers
A is either 45° or 135°.
To prove the given statement, let's assume that the points B and C lie on a coordinate plane, with the origin (0, 0) as the common vertex of the right angles at points B, C, and A. Let the coordinates of points B and C be (x₁, y₁) and (x₂, y₂) respectively.
Using the distance formula, we have:
AB² = x₁² + y₁²
AC² = x₂² + y₂²
According to the given equation, +b4+c4 = 20² (b²+c²), we can rewrite it as:
(x₁² + y₁²) + (x₂² + y₂²) = 20² [(x₁² + y₁²) + (x₂² + y₂²)]
Expanding and simplifying the equation, we get:
x₁² + y₁² + x₂² + y₂² = 20² (x₁² + y₁² + x₂² + y₂²)
This equation can be further simplified to:
(x₁² + y₁²) + (x₂² + y₂²) = (20² - 1) (x₁² + y₁² + x₂² + y₂²)
Since the left side represents the sum of the squares of the distances from the origin to points B and C, and the right side is a constant multiplied by the same sum, we can conclude that the points B and C must lie on a circle centered at the origin.
In a circle, the sum of angles subtended by two perpendicular chords at the center is either 180° or 360°. Since the given problem involves right angles, we consider the sum of angles to be 180°.
For more questions on distance formulae
https://brainly.com/question/661229
#SPJ8
Suppose a basketball player has made 359 out of 449 free throws. If the player makes the next 3 free throws, I will pay you $39. Otherwise you pay me $43.
Step 1 of 2 : Find the expected value of the proposition
Answers
The expected value of the proposition is $22.6
How to determine the expected value?The given parameters are
Proportions of free throws = 359 out of 449Amount paid for making a throw = $39Amount collected for losing a throw = $43Represent the proportion as a fraction
So, we have
p = 359/449
The expected value is then calculated as
E(x) = p * Amount paid for making a throw - (1 - p) * Amount collected for losing a throw
Where p represents the proportion defined above
So, we have
E(x) = 359/449 * 39 - (1 - 359/449) * 43
Evaluate the difference
E(x) = 359/449 * 39 - 90/449 * 43
So, we have
E(x) = 22.6
Hence, the proposition has an expected value of $22.6
Read more about expected value at
https://brainly.com/question/15858152
#SPJ1
Answer:
-1.09
The problem requires one to calculate the win payoff and win probability as well as the lose payoff and probability. You would then do a calculation like this:
[(Win Payoff) x (Win Probability)] + [(Lose Payoff) x (Lose Probability)]
what is a correct interpretation of the expression 2 - (-5)
Answers
Detailed Explanation:
2 - (-5) will get simplified to 2 + 5.
This is because the negative symbols get cancelled and become positive as there are 2 of them.
Answer:
2+5
Step-by-step explanation:
A negative and a negative will make a positive.
En una escuela hay 200 estudiantes. Si la razón entre hombres estudiantes y mujeres
estudiantes es de 3:5, ¿cuántos estudiantes son hombres y cuántas son mujeres?
Answers
Answer:
75 hombres y 125 mujeres
Step-by-step explanation:
lo siento, yo no hablo español bien
Find the volume of a right circular cone that has a height of 15.2 cm and a base with a diameter of 11.9 cm. Round your answer to the nearest tenth of a cubic centimeter.
Answers
9514 1404 393
Answer:
563.5 cm³
Step-by-step explanation:
Use the formula for the volume of a cone:
V = (1/3)πr²h
Recognize that the radius is half the diameter:
r = (11.9 cm)/2 = 5.95 cm
V = (1/3)π(5.95 cm)²(15.2 cm) ≈ 563.516 cm³
The volume of the cone is about 563.5 cm³.
_____
Additional comment
If you use 3.14 for the value of π, then the result will be 563.2 cm³.
Toby has $65 to buy tshirts for his bowling team each tshirt costs $7 how many tshirts can he buy
Answers
11. In a geometric sequence, t₂ = 24 and t5 = 81. Calculate S7, to the nearest hundredth.
Answer: 514.75
Answers
Answer:
S₇ = 514.75
Step-by-step explanation:
the nth term of a geometric sequence is
\(t_{n}\) = a\(r^{n-1}\)
where a is the first term and r the common ratio
given t₂ = 24 and t₅ = 81 , then
ar = 24 → (1)
a\(r^{4}\) = 81 → (2)
divide (2) by (1) to eliminate a
\(\frac{ar^{4} }{ar}\) = \(\frac{81}{24}\)
r³ = \(\frac{81}{24}\) ( take cube root of both sides )
\(\sqrt[3]{r^{3} }\) = \(\sqrt[3]{\frac{81}{24} }\)
r = 1.5
substitute r = 1.5 into (1) and solve for a
a × 1.5 = 24 ( divide both sides by 1.5 )
a = 16
the sum to n terms of a geometric sequence is
\(S_{n}\) = \(\frac{a(r^{n}-1) }{r-1}\) , then
S₇ = \(\frac{16((1.5)^{7}-1)) }{1.5-1}\)
= \(\frac{16(17.0859375-1)}{1.5-1}\)
= \(\frac{16(16.0859375)}{0.5}\) ( divide 16 by 0.5 )
= 32 × 16.0859375
= 514.75