Brayden is saving money to buy a new bike after 2 weeks he saved $180 after 4 weeks he saved $260 write an equation that can be used to model the number of dollars y braden saves over x weeks write your answer in slope intercept form do not include any spaces in your answer
Answers
The slope-intercept form is
\(y=mx+b\)m is the slope
b is the y-intercept (value y at x = 0)
Since y represents the amount of money he saves and x represents the number of weeks, then
x = 2 and y = 180
x = 4 and y = 260
We will use them to find the slope
\(m=\frac{y2-y1}{x2-x1}\)Substitute y2 by 260 and y1 by 180, x2 by 4, and x1 by 2
\(\begin{gathered} m=\frac{260-180}{4-2} \\ m=\frac{80}{2} \\ m=40 \end{gathered}\)The equation is
\(y=40x+b\)To find b substitute x by 2 and y by 180
\(\begin{gathered} 180=40(2)+b \\ 180=80+b \end{gathered}\)Subtract 80 from both sides
\(\begin{gathered} 180-80=80-80+b \\ 100=b \end{gathered}\)The equation is
\(y=40x+100\)Related Questions
2x²-2x-5=0
solve it using Δ=b²-4ac
Answers
Answer:
44
Step-by-step explanation:
1
Q2
Q3
Q4
Q5
Q6
Q7
Q8
Q୨
Q10
E
Rounding each number to the nearest 5, estimate the answer to the following
calculation: 52 x 63
Submit Answer
Skip for Now

Answers
Answer:
3280
Step-by-step explanation:
52×63=3276
Round 3276 to 3280
Hope this helps! :)
Hey, I was wondering if you could help me with this problem, I understand how to do these types of problems but this particular question confused me.

Answers
Solution:
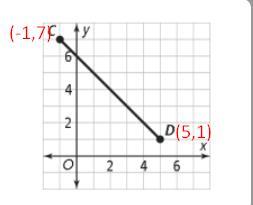
Given:
The point C is (-1,7) and the point D is (5,1).
To point that partitions CD in the ratio 3:1 is gotten using the formula;
where;
\(\begin{gathered} a=3,b=1 \\ x_1=-1,y_1=7 \\ x_2=5,y_2=1 \end{gathered}\)Substituting these values into the equation;
\(\begin{gathered} (x,y)=(\frac{1(-1)+3(5)}{1+3},\frac{1(7)+3(1)}{1+3}) \\ (x,y)=(\frac{-1+15}{4},\frac{7+3}{4}) \\ (x,y)=(\frac{14}{4},\frac{10}{4}) \\ (x,y)=(3.5,2.5) \end{gathered}\)Therefore, the point that partitions the line segment CD in the ratio 3:1 is (3.5,2.5)
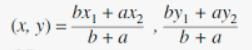
a high school sells students tickets for $5 as well as general admission tickets for $7 to attend thier football games. The school needs to bring in at least $1500 per game in order to maintain the costs of the football team
Answers
The cost of students ticket is $37.5and the cost of general admission is $187.5.
What is system of equations?A finite set of equations for which common solutions are sought is referred to in mathematics as a set of simultaneous equations, also known as a system of equations or an equation system.
Assume s be the students tickets cost and g be the general admission cost.
From the given information,
⇒ s + g = 225 ..(1)
5s + 7g = 1500 ..(2)
From equation (1),
s = 225 - g
Plug the value of s in equation (2)
5(225 - g) + 7g = 1500
1125 - 5g + 7g = 1500
2g = 1500 - 1125
2g = 375
g = 187.5
Plug g = 125 in equation (1),
s + 187.5= 225
s = 225 - 187.5
s = 37.5
To know more about system of equations, click on the link
brainly.com/question/13729904
#SPJ1
Evaluate the expression when x=35 and y=6 x / 5 - y
Answers
Answer:Variable expressions are expressions that involve variables, which are symbols that represent changing quantities. The value of the expression will change as the value of the variable changes.
For example, let's say with have the equation
x
+
5
When
x
=
1
, then
x
+
5
=
6
When
x
=
2
then
x
+
5
=
7
Hope that was helpful.
It is also known that customers will spend an average of $178 on additional maintenance. The standard deviation of the expenses is $50. If a simple random sample of 100 customers is taken: What is the probability that the sample mean will be between 166.75 and $170.50
Answers
Answer:
probability that the sample mean will be between 166.75 and $170.50 = 0.42816
Step-by-step explanation:
We are given;
Mean; μ = $178
Standard deviation; σ = $50
Now, we want to find the probability that the sample mean will be between $166.75 and $170.50.
Thus, we'll use the z-score formula;
z = (x - μ)/σ
So;
Lower limit of z is;
z = (166.75 - 178)/50
z = -0.225
Upper limit of z is;
z = (170.50 - 178)/50
z = -0.15
From the z-distribution table attached, the area between -0.225 and -0.15 is;
0.44038 - 0.01222 = 0.42816

A game is played using ne die. If the die is rolled and shows 3, the player wins $45. If the die shows any number other than 3, the player wins nothing. If there is a charge of $9 to play the game, what is the game's expected value?
Answers
Answer:
-$13.5
Step-by-step explanation:
Let x be a random variable of a count of player gain.
- We are told that if the die shows 3, the player wins $45.
- there is a charge of $9 to play the game
If he wins, he gains; 45 - 9 = $36
If he looses, he has a net gain which is a loss = -$9
Thus, the x-values are; (36, -9)
Probability of getting a 3 which is a win is P(X) = 1/6 since there are 6 numbers on the dice and probability of getting any other number is P(X) = 5/6
Thus;
E(X) = Σ(x•P(X)) = (1/6)(36) + (5/6)(-9)
E(X) = (1/6)(36 - (5 × 9))
E(X) = (1/6)(36 - 45)
E(X) = -9/6 = -3/2
E(X) = -3/2
This represents -3/2 of $9 = -(3/2) × 9 = - 27/2 = -$13.5
Write the set in set builder notation
16,17,18,19
Answers
The set in set builder notation is written as;
A = { x | 16 ≤ x ≤ 19 , x ∈ |N }
What is Set builder notation?
In a set-builder notation all the elements of the set must possess a single property to become the member of that same set.
The set is given as;
⇒ 16, 17, 18, 19
Now, In set builder notation it can be written as,
⇒ A = { x | 16 ≤ x ≤ 19 , x ∈ |N }
Where, 'A' is set defined for the given data set.
So, The set in set builder notation is written as;
A = { x | 16 ≤ x ≤ 19 , x ∈ |N }
Learn more about the set builder notation visit:
https://brainly.com/question/14657951
#SPJ1
not allowed
The table shows information about the masses of some dogs.
a) Work out the minimum number of dogs that could have a mass of more than
26 kg.
b) Work out the maximum number of dogs that could have a mass of more than
26 kg.
Mass, x (kg)
0≤x≤10
10≤x≤20
20≤x≤30
30 < 10
Frequency
8
11
5

Answers
Based on the frequency table given,
a) The minimum number of dogs that could have a mass of more than 26 kg is of: 5.
b) The maximum number of dogs that could have a mass of more than 26 kg is of: 16.
How is this so?The frequency table displays the number of times each value, or range of values, appears in the data-set.
where 11 weights are between 20 and 30, and all of the dogs in the interval 20 × 30 have weights less than 26 kg, the lowest number of dogs that might have a mass more than 26 kg is 5.
This implies that only the dogs in the period 30 x 40 would have a mass greater than 26 kg.
Learn more about Frequency Table:
https://brainly.com/question/16148316
#SPJ1
Learn more about maximum values;
https://brainly.com/question/30236354
#SPJ1
If x^2+y^2=0, what is the value of 2x-7y?
Answers
Answer:
Answer will be zero , since the value of x and y are zero and any value multiply with zero will be zero only .
What is the volume of a cone
Answers
7).
2. Hot Text: For each graph, choose the correct sentence to describe the graph.
The graph represents a proportional relationship.
The graph does not represent a proportional relationship.

Answers
a. The graph represents a proportional relationship.
b. The graph does not represent a proportional relationship.
c. The graph does not represent a proportional relationship.
d. The graph represents a proportional relationship.
What is a proportional relationship?A proportional relationship is a relationship in which a constant ratio between the output variable and the input variable exists.
The equation that defines the proportional relationship is a linear function with slope k and intercept zero presented as follows:
y = kx.
Hence graphs a and d represent proportional relationship, as they have intercepts at the origin.
A similar problem, also featuring proportional relationships, is presented at https://brainly.com/question/7723640
#SPJ1
How many 250ml glasses can be filled with 2l of water?
Answers
Answer:
8 glasses
Step-by-step explanation:
2L = 2,000 mL. 2000mL/250mL = 8 glasses
A complex shape combined frim a square and rectangle b=6, c=8, and d=12 what is the area of this complex figure?
Answers
The area of the complex figure is 132 square units
How to determine the area
From the information given, we have that the composite shape is a combination of a:
SquareRectangleThe formula for area of a square is given as:
Area = a ²
Where 'a' is the length of it side
Area = 6²
Area of square = 36 square units
The formula for area of a rectangle is given as:
Area = width × length
Area = 8 × 12
Area of rectangle = 96 square units
Area of the complex figure = Area of square + area of rectangle
= 36 + 96
= 132 square units
Thus, the area of the complex figure is 132 square units
Learn more about area here:
https://brainly.com/question/25292087
#SPJ1
What is 6^4written in expanded form?
4+4+4+4+4+4
4.4.4.4.4.4
6+6+6+6
6.6.6.6

Answers
Answer:
6 · 6 · 6 · 6
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
This is because the 4 is an exponent or a power.
This makes the 6 in this case multiply itself 4 times.
HOPE THIS HELPS
plz help it is kind of easy i will give alot of points to anyone that knows the answers

Answers
B. 26 years
i think..
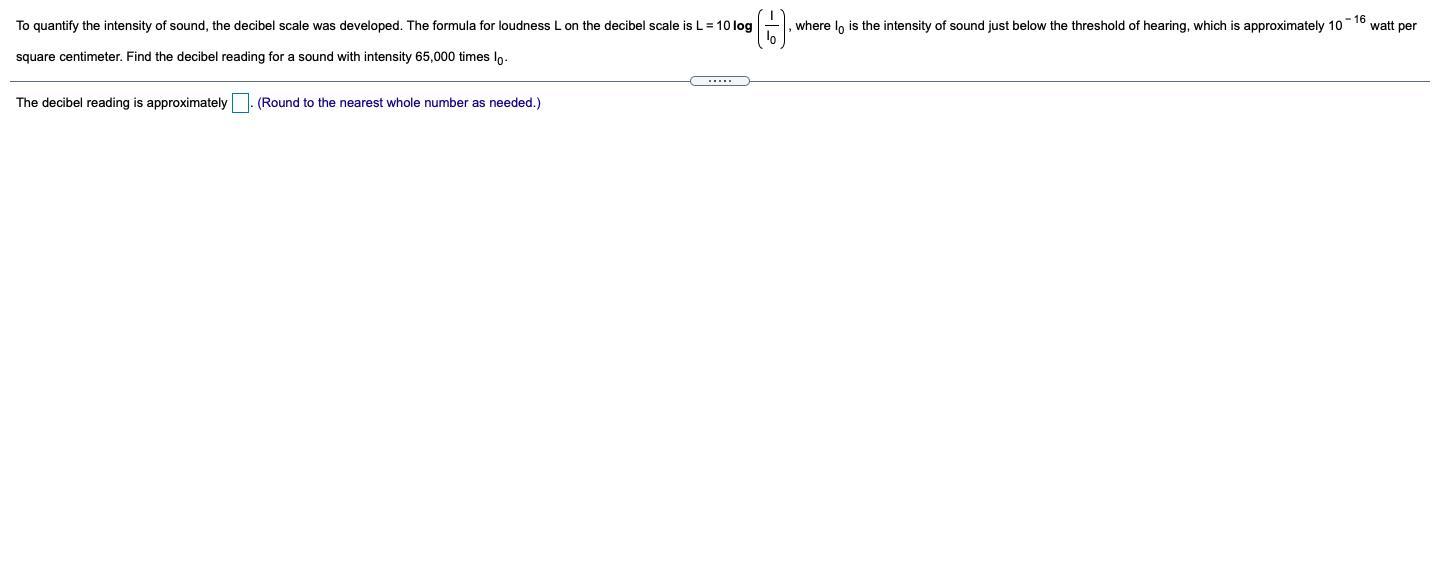
To quantify the intensity of sound, the decibel scale was developed. The formula for loudness L on the decibel scale is L=10logII0, where I0 is the intensity of sound just below the threshold of hearing, which is approximately 10−16 watt per square centimeter. Find the decibel reading for a sound with intensity 65,000 times I0.
Answers
Substitute the following values to the given formula for loudness and we get
\(\begin{gathered} L=10\log (\frac{I}{I_0}) \\ L=10\log (\frac{65000\times10^{-16}\text{ }W\/cm^2}{10^{-16}\text{ }W\/cm^2}) \\ L=10\log (65000) \\ L=48.12913357dB \\ L=48dB\text{ (rounded off to nearest whole number)} \end{gathered}\)Therefore, the decibel reading is approximately 48 dB.
Condense each Logarithm

Answers
The equation of logarithm are solved and
a) A = 2 + 3 log x + 4 log b
b) B = ( 36 + x + y ) ( log 6 )
c) C = ( 1/2 )x log 5
d) D = ln ( x⁴ / y² )
Given data ,
Let the logarithmic equation be represented as A
Now , the value of A is
a)
A = 2 log 10 + 3 log x + 4 log b
The base of the logarithm is 10 , so
A = 2 + 3 log x + 4 log b
b)
B = log 6³⁶ + log 6ˣ - log 6^ ( y )
From the properties of logarithm , we get
log A + log B = log AB
log A − log B = log A/B
log Aⁿ = n log A
B = 36 log 6 + x log 6 + y log 6
On taking the common term , we get
B = ( 36 + x + y ) ( log 6 )
c)
C = ( 1/2 )log 5ˣ
From the properties of logarithm , we get
C = ( 1/2 )x log 5
d)
D = 4 ln x - 2 ln y
From the properties of logarithm , we get
D = ln x⁴ - ln y²
On further simplification , we get
D = ln ( x⁴ / y² )
Hence , the logarithmic equations are solved
To learn more about logarithm click :
https://brainly.com/question/12049968
#SPJ1
find the product. write your answer in exponential form 8^-9 x 8^4
Answers
Answer:
\(8^{-5}\)
Step-by-step explanation:
When both terms share the same base, and you are multiplying, you are really adding the variables. Add:
\(8^{-9} * 8^{4}\\ = 8^{-9 + 4} = 8^{-5}\\\\8^{-5}\)is your answer.
~
3:Let f be a quadratic function such that
f(x) = ax² +bx+c = a (x-h)² + k
If k < 0, for what values of a will f(x) have no real zeros?
O a=0
O a<0
O azo
4.
O a>0
O aso
none of the answer choices

Answers
Answer:
O a=0
Step-by-step explanation:
what is the trend of the graph of the equation y = 3x + 10
Answers
Answer:
3x+y-10
Step-by-step explanation:
please Mark my answer in brainlist
Which expression are equivalent to the expression X minus Y times 5÷8-1÷4 X plus Y
Answers
The expression (X - Y) 5 ÷ 8 - 1 ÷ 4 (X + Y) is equivalent to
(20X² - 20Y² - 1) / (4X + 4Y)
We have,
We can simplify the given expression as follows:
(X - Y) 5 ÷ 8 - 1 ÷ 4 (X + Y)
= (5X - 5Y) ÷ 8 - 1 ÷ (4X + 4Y)
[distributing the factors]
= (5X - 5Y) /8 - 1/(4X + 4Y)
[finding a common denominator]
= ((5X - 5Y)(4X + 4Y) - 1)/(4X + 4Y)
= (20X² + 20XY - 20XY - 20Y² - 1) / (4X + 4Y)
= (20X² - 20Y² - 1) / (4X + 4Y)
Therefore,
The expression (X - Y) 5 ÷ 8 - 1 ÷ 4 (X + Y) is equivalent to
(20X² - 20Y² - 1) / (4X + 4Y)
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
A new cylindrical can with a diameter of 4cm is being designed by a local company. The surface area of the can is 140 square centimeters. What is the height of the can? Estimate using 3.14 for pi and round to the nearest hundredth. Apply the formula for the surface area of a cylinder SA=2B+Ph
Answers
The height of the can of cylinder shape is 9.14 cm.
What is a cylinder?
In mathematics, a cylinder is a three-dimensional solid that maintains two parallel bases separated by a curved surface at a specific distance. These bases frequently have a circular shape (like a circle), and an axis connects their respective centres.
We are given the diameter as 4 cm.
So, the radius is 2cm.
Also, it is given that the surface area of the can is 140 square centimeters.
So, using the surface area of cylinder, we get
⇒Area = 2πr (h + r)
⇒140 = 2π * 2 (h + 2)
⇒140 = 4π (h + 2)
⇒140 = 4 * 3.14 * (h + 2)
⇒140 = 12.56 * (h + 2)
⇒11.14 = h + 2
⇒h = 9.14
Hence, the height of the can of cylinder shape is 9.14 cm.
Learn more about cylinder from the given link
https://brainly.com/question/27440983
#SPJ1
What time would be written as 17:45 on the 24-hour clock?
5:45 p.m.
5:45 a.m.
7:45 p.m.
7:45 a.m
Answers
Answer:
5:45
Step-by-step explanation:
Answer:
5:45 p.m.
If you look when the time goes past 12:00 p.m. it can go to 24 hour clock and if you count 17 is 5.
The residents of a city voted on whether to raise property taxes. The ratio of yes votes to no votes was 5 to 8. If there were 9854 total votes, how many no votes were there?
Answers
There were approximately 6056 no votes.
Let's assume the number of yes votes is represented by the variable "5x," where x is a positive constant.
Similarly, the number of no votes can be represented by "8x" since the ratio of yes votes to no votes is 5 to 8.
The total number of votes is given as 9854, so we can set up the following equation:
\(5x + 8x = 9854\)
Combining like terms, we have:
\(13x = 9854\)
To solve for x, we divide both sides of the equation by 13:
\(x = \frac{9854 }{13}\)
\(x \approx 757.23\)
Since x represents a positive constant, we round it to the nearest whole number, giving us x = 757.
Now, we can find the number of no votes by multiplying x by the ratio of no votes:
No votes \(= 8x\)
\(= 8 \times 757\)
\(= 6056\)
Therefore, there were approximately 6056 no votes.
For such more questions on votes
https://brainly.com/question/32031211
#SPJ8
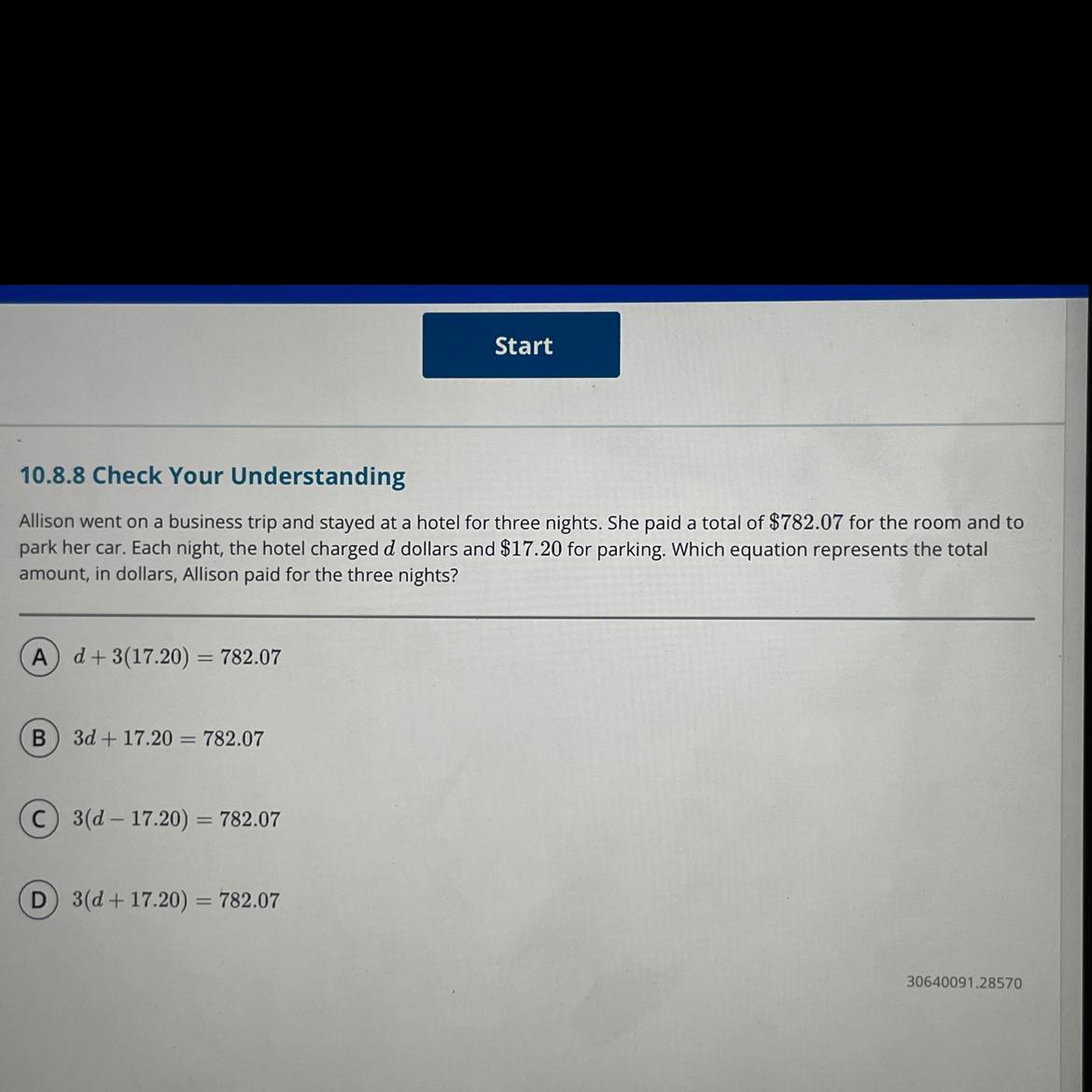
10.8.8 Check Your Understanding
Allison went on a business trip and stayed at a hotel for three nights. She paid a total of $782.07 for the room and to
park her car. Each night, the hotel charged d dollars and $17.20 for parking. Which equation represents the total
amount, in dollars, Allison paid for the three nights?
A) d+3(17.20) = 782.07
(B) 3d+17.20 = 782.07
C) 3(d-17.20) = 782.07
D) 3(d+17.20) = 782.07
Answers
We can see that the correct equation that can depict the problem is 3(d+17.20) = 782.07. Option D
Which equation shows the total charge?We have to look at the problem that we have here. In the case of the question that we have been asked, we can see that for the problem that has been given here, it is clear that; Allison went on a business trip and stayed at a hotel for three nights. She paid a total of $782.07 for the room and to park her car.
If it is known that Each night, the hotel charged d dollars and $17.20 for parking. We can say that let the amount that is charged for the lodging be d and we have the equation as; 3(d+17.20) = 782.07.
Learn more about equation:https://brainly.com/question/29657983
#SPJ1
The blue dot is at what value on the number line? 8 12
Answers
8 and 12 are separated by 1 line, and they have a difference of 4 units, so..
count every two lines and add 4 units
this means that the blue dot is 20
The fairy fly is one of the world’s smallest insects. It may measure no more than 1.39×10−4 meter in length. What is the total length of 2 of these insects, placed end to end?
Answers
Answer: The length of one fairy fly is 1.39×10−4 meter. To find the total length of two fairy flies placed end to end, we need to add their lengths.
1 fairy fly = 1.39×10−4 meter
2 fairy flies = 2 × 1.39×10−4 meter (adding the lengths of two fairy flies)
= 2.78×10−4 meter
Therefore, the total length of two fairy flies placed end to end is 2.78×10−4 meter.
Step-by-step explanation:
A circular pool measures 12 feet across. One cubic yard of concrete is to be used to create a circular border of uniform width around the pool. If the border is to have a depth of 6 inches, how wide will the border be?
Answers
SOLUTION:
Step 1:
In this question, we are given the following:
A circular pool measures 12 feet across.
One cubic yard of concrete is to be used to create a circular border of uniform width around the pool.
If the border is to have a depth of 6 inches, how wide will the border be?
Step 2:
From the question, we can see that:
\(6\text{ inches = 0. 5 feet}\)\(1\text{ cubic yard = 3 ft x 3ft x 3ft = }27ft^3\)\(\begin{gathered} \text{Let the radius of the pool = ( 6+x ) feet} \\ \text{Let the width of the concrete that is used to } \\ \text{create the circular border = 6 feet} \end{gathered}\)\(\text{Let the depth of the border = 6 inches = }\frac{6}{12}=\text{ 0. 5 inches}\)Step 3:
\(\begin{gathered} U\sin g\text{ } \\ \pi R^2h\text{ - }\pi r^2\text{ h = 27} \\ \pi(6+x)^2\text{ 0. 5 - }\pi(6)^2\text{ 0. 5 = 27} \\ \text{0. 5}\pi(x^2\text{ + 12x + 36 - 36 ) = 27} \\ 0.\text{ 5 }\pi(x^2\text{ + 12 x) = 27} \\ \text{Divide both sides by 0. 5 }\pi\text{ , we have that:} \end{gathered}\)\(x^2\text{ + 12 x - (}\frac{27}{0.\text{ 5}\pi})=\text{ 0}\)Solving this, we have that:
CONCLUSION:
From the calculations above, we can see that the value of the x:
( which is the width of the border ) = 1. 293 feet
(correct to 3 decimal places)



A coupon book has a coupon for 10% off a ticket at a theme park. A ticket usually costs $80. How much would a visitor save with the coupon?
Answers
Answer: the visitor would save $8 with the coupon.
Step-by-step explanation: 10% of $80 = 0.1 x $80 = $8