Brenda needs to solve the system of linear equations below for her homework assignment. y = 9x – 70 y = 2x – 32 Which is a reasonable estimate of the solution to this system of linear equations?
A. (8, -25
B. (7, -24)
C. (5, -22)
D. (3, -20)
Answers
Answer:
C (5, -22) is the answer
Related Questions
Making a round trip from Fairview to Cartersville, a distance of 20 miles, a pilot faces 30 mph head wind one way and 30 mph tail wind on the return trip. The return trip takes 45 minutes less than the outbound journey. Find the speed of the plane in still air
Answers
Answer:
50mph
Step-by-step explanation:
Given the following :
Distance (d) of journey = 20 miles
Wind speed = 30mph head wind in one way, 30mph tail wind in the other direction
Return trip = 45 minutes (45/60 = 0.75 hour) less Than the outbound journey
Speed of plane in still air
Outbound trip :
Velocity = Distance / time
Time = distance / velocity
Velocity = (v - 30) due to head wind
Return Velocity (V +30) due to tail wind
Outbound time = return distance
20 / (v - 30) = 20 / (v +30) + 0.75
20v + 600 = 20v + 0.75v^2 + 22.5v - 600-22.5v-675
600 = 0.75v^2 - 1275
0.75v^2 = 1875
v^2 = 1875/ 0.75
v^2 = 2500
v = sqrt(2500)
v = 50mph
Geometry - No links please
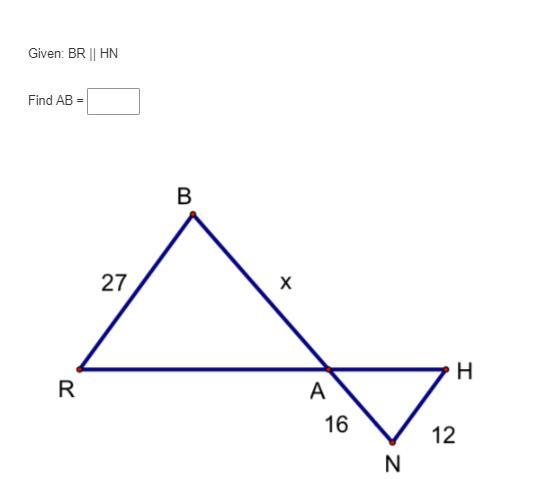
Answers
Answer:
36
Step-by-step explanation:
\( In\: \triangle ABR \:\&\: \triangle ANH\)
BR || HN(Given)
Therefore,
\( \angle ABR \cong \angle ANH\) (Alternate angles)
\( \angle BAR \cong \angle HAN\) (Vertical angles)
\( \therefore \triangle ABR \sim \triangle ANH\) (AA postulate)
\( \therefore \frac{AB}{AN} =\frac{BR}{HN} \) (csst)
\( \therefore \frac{x}{16} =\frac{27}{12} \)
\( \therefore \frac{x}{16} =\frac{9}{4} \)
\( \therefore x =\frac{9\times 16}{4} \)
\( \therefore x ={9\times 4} \)
\( \therefore x =36 \)
3.7) For a long time period, if a watershed receives 300 mm of
precipitation and has a 200 mm evapotranspiration annually,
determine annual average runofff.
Answers
The annual average runoff for the watershed is 100 mm.
To determine the annual average runoff, we need to calculate the difference between the precipitation and evapotranspiration.
Given:
Precipitation = 300 mm
Evapotranspiration = 200 mm
To find the annual average runoff, we subtract the evapotranspiration from the precipitation:
Annual Average Runoff = Precipitation - Evapotranspiration
Annual Average Runoff = 300 mm - 200 mm
Annual Average Runoff = 100 mm
Therefore, The watershed's average annual runoff is 100 mm.
learn more about average from given link
https://brainly.com/question/130657
#SPJ11
a unit of measurement equal to one thousand meters is_____
Answers
A unit of measurement which is equal to one thousands meters is known as one kilometers.
Different units of measurements are meters , kilometers, centimeters, millimeters and so on.Measuring small length basically we use centimeters and very small length in millimeters.Measuring medium length we use unit known as meters.When we have measure long distance unit which is used is known as kilometers.Relation between different units of length are:1centimeters is equal to 10 millimeters1 meter is equal to 100 centimeters1 kilometers is equal to 1000 metersTherefore, the given units of measurement equal to one thousand meters is called one - kilometers.
Learn more about units here
brainly.com/question/10433377
#SPJ4
What is 4/6 dived by 3/12
Answers
Answer:
8/3
Step-by-step explanation:
Lori and Mike Boyd have a combined monthly gross income of $13,395.00. Their records show that last year they paid $25,484.60 in mortgage payments, $1,356.00 for insurance premiums, and $12,240 in annual real estate taxes. They also had the annual expenses shown. Did they stay within the FHA recommendation?
Answers
Lori and Mike Boyd both they stay within the FHA recommendation.
What is the FHA recommendation?
FHA loans come in 15-year and 30-year terms with fixed interest rates. The agency's flexible underwriting standards are designed to help give borrowers who might not qualify for private mortgages a chance to become homeowners
To calculate this:
Total annual expenses = Mortgage payments + Insurance premiums + Real estate taxes
With the values:
\(T== $25,484.60 + $1,356.00 + $12,240\\T== $39,080.60\)
Make this a monthly expanses:
\(T= $39,080.60 / 12\\T= $3,256.72\)
Calculate the gross income:
Monthly expenses / Monthly gross income
With the values:
\(3,256.72 / 13,395.00=0.243\)
If you put this value in percentage will be 24.3% which is low than 43%, so we can say that both are in the FHA recommendation.
See more about finances at brainly.com/question/30307509
#SPJ1
Ramon is graphing the function f(x) = 3(4)x. He begins by plotting the initial value. Which graph represents his initial step?
On a coordinate plane, the point (0, 3) is graphed.
On a coordinate plane, the point (0, 4) is graphed.
On a coordinate plane, the point (3, 0) is graphed.
On a coordinate plane, the point (4, 0) is graphed.
Answers
The graph that represents Ramon's initial step is, On a coordinate plane, the point (0, 3) is graphed.
What is an ordered pair?The ordinate and abscissa of the x coordinate, along with two values specified in parentheses in a specific order, make up an ordered pair.
Pair in Order = (x, y) where x represents the abscissa, the measure of a point's separation from the main axis, and y represents the ordinate, the measure of a point's separation from the secondary axis.
Given, Ramon is graphing the function f(x) = 3 + (4)x.
We know the initial value of a function is determined when the independent variable is set to zero.
Here the independent variable is 'x'.
Now, at x = 0,
f(0) = 3 + (4)(0).
f(0) = 3.
So, The ordered pair is (0, 3).
learn more about the ordered pair here :
https://brainly.com/question/28874341
#SPJ1
Answer:
a
Step-by-step explanation:
6.30 in fraction help
Answers
Answer:
63/10
Step-by-step explanation:
...............i think
Answer:
63/10 would be a simplified fraction
Step-by-step explanation:
You convert 6.30 to a mixed number by placing the numbers right of the decimal over 10, reduce the fraction, then convert it to ana improper fraction by multiplying the denominatior by the whole number and adding the numerator to get a new numerator. You then place this over the original denominator
Here is a right-angled triangle.
y cm
8.2 cm
12.3 cm
Work out the value of y.
Give your answer correct to 1 decimal place.
Answers
Answer:
9.1
Step-by-step explanation:
Let,
hypotenuse = 12.3 cm
perpendicular = 8.2 cm
base = y cm
(hypotenuse)^2 = (perpendicular)^2 + (base)^2
(12.3)^2 = (8.2)^2 + y^2
151.29 = 67.24 + y^2
151.29 - 67.24 = y^2
.: y^2 = 84.05
y = √84.05
y = 9.1
Solve for m.
-9 - m = -4 – 2m
m =
Answers
Answer:
m = 5
Step-by-step explanation:
-9 - m = -4 -2m
-m = -4 +9 - 2m
-m = 5 -2m
2m - m = 5
m = 5
Sam is building a cutlery holder for his wife.he wants to slope to be 0.7 calculate the height of each vertical column, labeled 'a', 'b', 'c','d','e'
Answers
In order to build a cutlery holder with a slope of 0.7, Sam needs to determine the height of each vertical column, labeled 'a', 'b', 'c', 'd', and 'e'. Sam will be able to create a cutlery holder with a slope of 0.7.
To calculate the height of each vertical column, Sam needs to understand the concept of slope. Slope is the ratio of the vertical change (rise) to the horizontal change (run). In this case, the slope is given as 0.7.
Let's assume that the horizontal distance between each column is equal. We can assign a standard value of 1 unit for the horizontal run between columns.
To find the vertical rise for each column, we can multiply the horizontal run by the slope. Therefore, the height of column 'a' would be 0.7 units, column 'b' would be 1.4 units (0.7 * 2), column 'c' would be 2.1 units (0.7 * 3), column 'd' would be 2.8 units (0.7 * 4), and column 'e' would be 3.5 units (0.7 * 5).
By assigning these respective heights to each vertical column, Sam will be able to create a cutlery holder with a slope of 0.7.
Learn more about slope here:
https://brainly.com/question/3605446
#SPJ11
what is the general solution to the differential equation dydx=cos(8x)cos(4y)dydx=cos(8x)cos(4y) ?
Answers
The general solution to the differential equation `dy/dx = cos(8x)cos(4y)` is given below:Main Answer:Separating the variables in the given differential equation, we have `dy/cos(4y) = cos(8x) dx`Integrating both sides, we get:`1/4 sin(4y) = 1/8 sin(8x) + C`where C is the constant of integration.
Now, solving for y, we get:`y = 1/4 sin^{-1}(2sin(8x) + C)`where `sin^{-1}` denotes the inverse of sine function. So, this is the general solution to the given differential equation.Explanation:Given differential equation:`dy/dx = cos(8x)cos(4y)`Separating the variables:`dy/cos(4y) = cos(8x) dx`Integrating both sides:`∫ dy/cos(4y) = ∫ cos(8x) dx``1/4 ∫ sec^2(4y) dy = 1/8 sin(8x) + C``1/4 tan(4y) = 1/8 sin(8x) + C`
Now, solving for y:`tan(4y) = 1/2 sin(8x) + C`Dividing both sides by 4, we get:`y = 1/4 tan^{-1}(1/2 sin(8x) + C)`However, the inverse of the tangent function is a bit messy, so we use the identity:`tan^{-1}(x) = 1/2 i ln((i+x)/(i-x))`where `i` is the imaginary unit. Plugging in, we get:`y = 1/4 i ln((i+1/2 sin(8x) + C)/(i-1/2 sin(8x) - C))`This is the general solution to the given differential equation.
To know more about integration visit:
https://brainly.com/question/31744185
#SPJ11
3
Consider the following number pattern.
2; 18; 7; 12; 12; 6; 17......
(a) Write the next two terms of the sequence.
Answers
Answer:
...; 0; 22
Step-by-step explanation:
The pattern appears to consist of two interleaved arithmetic sequences.
__
Odd-numbered terms increase by 5: 2, 7, 12, 17, 22.
Even-numbered terms decrease by 6: 18, 12, 6, 0.
The next two terms are 0 and 22.
Convert 250.025 to a mixed number
Answers
Answer:
1/5
Step-by-step explanation:
It's already a mixed number.
The whole number part is 250 .
The fraction part is 0.025 . (Same thing as 1/40 .)
Done
.at the beginning of every period of british literature, mrs. crabapple picks a random student to receive a crabapple as a gift, but really, as you might imagine, they are quite bitter and nasty. given that there are $11$ students in her class and her class meets four times a week, how many different sequences of crabapple recipients are possible in a week?
Answers
The number of different sequences of crabapple recipients that are possible in a week are 14,641.
In Mrs. Crabapple's British literature class, there are 11 students, and she gives out a crabapple at the beginning of each of the 4 class meetings per week.
To determine the number of different sequences of crabapple recipients, we will calculate the number of possibilities for each class meeting and multiply them together. Since she can pick any of the 11 students for each class, there are:
11 possibilities for the first class,
11 possibilities for the second class,
11 possibilities for the third class, and
11 possibilities for the fourth class.
So, the total number of different sequences of crabapple recipients in a week is:
11 * 11 * 11 * 11 = 11^4 = 14,641 different sequences.
To learn more about students, click here
https://brainly.com/question/17332524
#SPJ11
A cattle farmer wants to save for his daughter's college tuition. He will have to pay P50,000 at the end of every year for the next four years that his daughter attends college. He has 8 years until his daughter starts college to save up for her tuition. Using a 7\% interest rate compounded annually, what is the amount the farmer would have to save every year for the 8 years?
Answers
Calculating this expression will give us the amount the farmer needs to save annually over the 8-year period.
Given:
Payment required at the end of each year: P50,000
Number of years until the daughter starts college: 8
Interest rate: 7% (compounded annually)
We can calculate the annual savings using the formula for the present value of an ordinary annuity:
P = \dfrac{PMT \times (1 - (1 + r)^{-n}{r}
Where:
P = Present value (amount to be saved annually)
PMT = Payment amount (P50,000)
r = Interest rate per period (7% or 0.07)
n = Number of periods (8)
Let's substitute the given values into the formula:
\[ P = \dfrac{50,000 \times (1 - (1 + 0.07)^{-8}{0.07} \]
Calculating this expression will give us the amount the farmer needs to save annually over the 8-year period.
Learn more about Annual Income here:
https://brainly.in/question/54172772
#SPJ11
is this true or false? f (n )equals o (g (n ))space a n d space g (n )equals o (f (n ))space t h e n space f (n )equals theta (g (n ))
Answers
The statement "f(n) equals O(g(n)) and g(n) equals O(f(n)) then f(n) equals Θ(g(n))" is true.
In computer science, the O-notation and Θ-notation are used to describe the upper and tight bounds, respectively, of the running time of an algorithm. O-notation provides an upper bound on the running time of an algorithm, while Θ-notation provides a tight bound, meaning that the running time of an algorithm is both upper-bounded and lower-bounded by a certain function.
When f(n) equals O(g(n)), it means that the growth rate of f(n) is upper-bounded by the growth rate of g(n). In other words, the running time of f(n) is no greater than that of g(n), multiplied by some constant factor.
When g(n) equals O(f(n)), it means that the growth rate of g(n) is upper-bounded by the growth rate of f(n). This implies that the running time of g(n) is no greater than that of f(n), multiplied by some constant factor.
If both f(n) equals O(g(n)) and g(n) equals O(f(n)), it can be concluded that the running time of f(n) and g(n) are asymptotically equivalent. This means that their growth rates are the same, and thus f(n) equals Θ(g(n)).
In conclusion, if f(n) equals O(g(n)) and g(n) equals O(f(n)), it is true that f(n) equals Θ(g(n)), which means that the two functions have the same growth rate. This property can be useful in comparing the running time of different algorithms or in analyzing the efficiency of algorithms.
For more such questions on computer algorithms
https://brainly.com/question/24953880
#SPJ4
there were x quarts of liquid in a con-tainer. first, 3 4 of the liquid in the container was removed. then another 1 2 quart was poured into the container. write an expression in terms of x for the number of quarts of liquid in the container at the end. then write another equivalent expres-sion.explain
Answers
The another equivalent expression of total liquid is (x+2)/4.
Expressions that perform similarly but differ in appearance are said to be equivalent expressions. When the same value for the variable is entered, two algebraic expressions that are equivalent will have the same result.
x quarts liquid in the container 3/4 part of liquid is removed
Then remaining liquid in container = X - \(\frac{3}{4}X\)
Then remaining liquid in container = x/4quarts
Another 1/2 quart is poured into container
Then total liquid = \(X-\frac{3}{4}X+\frac{1}{2}\) quarts
total liquid = \(\frac{X+2}{4}\) quarts
So, then the another equivalent expression of total liquid is (x+2)/4.
To learn more about simplification of expression link is here
brainly.com/question/14526172
#SPJ4
the chart gives prices and output information for the country of new zealand. use this information to calculate real and nominal gdp for both years. use 2017 as the base year.
Answers
The nominal GDP for the year 2017 is $87,000, and the real GDP for the year 2017 is $87,000.
How to calculate real and nominal GDP?Using a base year,the formula to calculate the Real GDP is given below:
Real GDP = Nominal GDP ÷ Deflator (in decimal)
Where, Deflator = (Price of base year goods and services ÷ Price of current year goods and services) × 100
Nominal GDP for the year 2017= 1,650 × 10 + 2,820 × 25= 16,500 + 70,500= 87,000
Nominal GDP for the year 2019= 1,900 × 12 + 3,250 × 27= 22,800 + 87,750= 110,550 Using the above formula,
Deflator for the year 2017 can be calculated as:
Deflator for 2017= (P2017 / P2017) × 100= (1 × 10 + 2 × 25) / (1 × 10 + 2 × 25) × 100= 100
Similarly, Deflator for the year 2019 can be calculated as:
Deflator for 2019= (P2019 / P2017) × 100= (1.10 × 12 + 2.75 × 27) / (1 × 10 + 2 × 25) × 100= 120.25
Now, Real GDP for the year 2017= 87,000 / 100= $87,000 Real GDP for the year 2019= 110,550 / 120.25= $917.54 million.
Thus, the nominal GDP for the year 2017 is $87,000, and the real GDP for the year 2017 is $87,000. The nominal GDP for the year 2019 is $110,550, and the real GDP for the year 2019 is $917.54 million.
Learn more about real and nominal GDP
brainly.com/question/15171681
#SPJ11
help please asap and thank you

Answers
Step-by-step explanation:
I am not sure I can see the room limitations.
what I see is that the kitchen is one large rectangle from
(-8, 8) to (0, 0).
the rec room is Amado one large rectangle from
(5, 6) to (8, -7).
I am basing the rest in this.
for the area calculations, please consider that the area of a rectangle is length × width, and the area of a triangle is half of the rectangle it splits in half with its baseline (as diagonal).
A)
area 1 =
rectangle (-8, 8) to (-5, 3)
plus
half of the rectangle (-5, 8) to (-3, 3)
3×5 + 1/2 × 2×5 = 3×5 + 1×5 = 15 + 5 = 20 yd²
area 2 =
half of the rectangle (-5, 8) to (-3, 3)
plus
rectangle (-3, 8) to (0, 3)
1/2 × 2×5 + 3×5 = 20 yd²
area 3 = area 4 =
half of the rectangle (-8, 3) to (0, 0)
1/2 × 8×3 = 4×3 = 12 yd²
B)
the total area of the kitchen is the sum of all 4 areas
20 + 20 + 12 + 12 = 64 yd²
we can also calculate this in general, seeing that the general dimensions of the kitchen are 8×8 : from (-8, 8) to (0, 0).
8×8 = 64 yd²
maximize x+y
subject to
2x+y≥32
2x-y≤16
10≤y≤20
x≥0
Answers
Answer:
This needs a graph
Step-by-step explanation:
do you have a graph there
Answer:
2x+y≥32
2x-y≤16
10≤y≤20
x≥0
200 = 1000 - n/4. What is the value of n? Show working out, please.
Answers
Answer:
n = 3200
Step-by-step explanation:
200 = 1000 - \(\frac{n}{4}\) ( subtract 1000 from both sides )
- 800 = - \(\frac{n}{4}\) ( multiply both sides by 4 to clear the fraction )
- 3200 = - n ( multiply both sides by - 1 )
n = 3200
Which rule describes the x-coordinates in the translation below?. 4 2 h 1 M * 3 us A.x+0
Bx+6
C.X-6
D.x+2
Answers
Answer:
3 = 6 h M
Step-by-step explanation:
4 = 2 h ⋅ ( 1 M )⋅ 3 = 6 h M
you answered one of my questions before now i answer yours lol.
Use Green's Theorem to evaluate oint_c xy^2 dx + x^5 dy', where 'C' is the rectangle with vertices (0,0), (3,0), (3,5), and (0,5)
Find and classify the critical points of z=(x^2 - 4 x)(y^2 - 5 y) Lo
Answers
To evaluate the line integral using Green's Theorem, we need to find the curl of the vector field and then calculate the double integral over the region enclosed by the curve. Answer : the critical points of the function z = (x^2 - 4x)(y^2 - 5y) are (x, y) = (0, 0) and (x, y) = (0, 4)
Given the vector field F = (xy^2, x^5), we can find its curl as follows:
∇ × F = (∂Q/∂x - ∂P/∂y)
where P is the x-component of F (xy^2) and Q is the y-component of F (x^5).
∂Q/∂x = ∂/∂x (x^5) = 5x^4
∂P/∂y = ∂/∂y (xy^2) = 2xy
Therefore, the curl of F is:
∇ × F = (2xy - 5x^4)
Now, we can apply Green's Theorem:
∮C P dx + Q dy = ∬D (∇ × F) dA
where D is the region enclosed by the curve C.
In this case, C is the rectangle with vertices (0,0), (3,0), (3,5), and (0,5), and D is the region enclosed by this rectangle.
The line integral becomes:
∮C xy^2 dx + x^5 dy = ∬D (2xy - 5x^4) dA
To evaluate the double integral, we integrate with respect to x first and then with respect to y:
∬D (2xy - 5x^4) dA = ∫[0,5] ∫[0,3] (2xy - 5x^4) dx dy
Now, we can calculate the integral using these limits of integration and the given expression.
As for the second part of your question, to find the critical points of the function z = (x^2 - 4x)(y^2 - 5y), we need to find the points where the partial derivatives with respect to x and y are both zero.
Let's calculate these partial derivatives:
∂z/∂x = 2x(y^2 - 5y) - 4(y^2 - 5y)
= 2xy^2 - 10xy - 4y^2 + 20y
∂z/∂y = (x^2 - 4x)(2y - 5) - 5(x^2 - 4x)
= 2xy^2 - 10xy - 4y^2 + 20y
Setting both partial derivatives equal to zero:
2xy^2 - 10xy - 4y^2 + 20y = 0
Simplifying:
2y(xy - 5x - 2y + 10) = 0
This equation gives us two cases:
1) 2y = 0, which implies y = 0.
2) xy - 5x - 2y + 10 = 0
From the second equation, we can solve for x in terms of y:
x = (2y - 10)/(y - 1)
Now, substitute this expression for x back into the first equation:
2y(2y - 10)/(y - 1) - 10(2y - 10)/(y - 1) - 4y^2 + 20y = 0
Simplifying and combining like terms:
4y^3 - 32y^2 + 64y = 0
Factoring out 4y:
4y(y^2 - 8y +
16) = 0
Simplifying:
4y(y - 4)^2 = 0
This equation gives us two cases:
1) 4y = 0, which implies y = 0.
2) (y - 4)^2 = 0, which implies y = 4.
So, the critical points of the function z = (x^2 - 4x)(y^2 - 5y) are (x, y) = (0, 0) and (x, y) = (0, 4).
To classify these critical points, we can use the second partial derivative test or examine the behavior of the function in the vicinity of these points.
Learn more about Green's Theorem : brainly.com/question/27549150
#SPJ11
1
2
3
45
6
7
8.
9
10
Ronald spent $134.15 on school clothes. He counted his money and discovered that he had $33.85
left. How much money did he originally have?
Enter an equation, using m as your variable, to find how much money he originally had. Then solve
the equation
An equation is
Ronald originally had s
Answers
Hello!
So, using simple equation format, an equation could be:
$134.15 + $33.85 = m
Now we have to add the products.
134.15
+ 33.85
__________
168
Originally, Ronald had $168.
waffletowne
1) Louis is dilating triangle ABC at right. He
multiplied each x-coordinate and y-coordinate of
triangle ABC by -2.
a. What are the new coordinates of the points?
Answers
To find the new coordinates of the points after Louis multiplied each x-coordinate and y-coordinate of triangle ABC by -2, we can use the following formulas:
New x-coordinate = -2 * old x-coordinate
New y-coordinate = -2 * old y-coordinate
Let's apply these formulas to each point in triangle ABC:
Point A: (-3, 4)
New x-coordinate of A = -2 * (-3) = 6
New y-coordinate of A = -2 * 4 = -8
New coordinates of A: (6, -8)
Point B: (1, 1)
New x-coordinate of B = -2 * 1 = -2
New y-coordinate of B = -2 * 1 = -2
New coordinates of B: (-2, -2)
Point C: (5, -2)
New x-coordinate of C = -2 * 5 = -10
New y-coordinate of C = -2 * (-2) = 4
New coordinates of C: (-10, 4)
Therefore, the new coordinates of the points after Louis multiplied each x-coordinate and y-coordinate of triangle ABC by -2 are:
A: (6, -8)
B: (-2, -2)
C: (-10, 4)
Look at the image below. Identify the coordinates for point X, so that the ratio of AX : XB = 5 : 4
Answers
The coordinates of X that partitions XY in the ratio 5 to 4 include the following: X (-1.6, -7).
How to determine the coordinates of point X?In this scenario, line ratio would be used to determine the coordinates of the point X on the directed line segment AB that partitions the segment into a ratio of 5 to 4.
In Mathematics and Geometry, line ratio can be used to determine the coordinates of X and this is modeled by this mathematical equation:
M(x, y) = [(mx₂ + nx₁)/(m + n)], [(my₂ + ny₁)/(m + n)]
By substituting the given parameters into the formula for line ratio, we have;
M(x, y) = [(5(2) + 4(-6))/(5 + 4)], [(5(-11) + 4(-2))/(5 + 4)]
M(x, y) = [(10 - 24)/(9)], [(-55 - 8)/9]
M(x, y) = [-14/9], [(-63)/9]
M(x, y) = (-1.6, -7)
Read more on line ratio here: brainly.com/question/14457392
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Which equation represents the hanger below. x represents the triangles while y represents the square
Answers
Answer:
Which equation represents the hanger below. x represents the triangles while y represents the square
Answer:
Step-by-step explanation:
so first divide
multiply and subtract
and think a little
there its easy :D
Stellan, an alien from the planet Tellurango, shoots a flaming projectile straight up into the air from the edge of a cliff that is 28 meters high. According to the laws of physics on his planet, the height of the projectile, h, after t seconds is modeled by a quadratic equation. The projectile reaches a maximum height of 64 meters after 6 seconds. What is the vertex form of the quadratic equation that represents the height, h, of the projectile after t seconds
Answers
The vertex form of the quadratic equation that represents the height, h, of the projectile after t seconds is given byy = -(x - 6)² + 64.
An alien from the planet Tellurango, shoots a flaming projectile straight up into the air from the edge of a cliff that is 28 meters high.The height of the projectile, h, after t seconds is modeled by a quadratic equation. The projectile reaches a maximum height of 64 meters after 6 seconds. Therefore, we can say that the vertex of the quadratic equation is (6,64).
Let's write the quadratic equation in the vertex form:y = a(x - h)² + ky = a(x - 6)² + 64
Here, the vertex of the quadratic equation is (h, k) = (6, 64)We have to find the value of "a". The value of "a" can be determined using the given points which are (0,28), (6,64).
The equation of the quadratic equation can be written as follows:y = a(x - h)² + ky = a(x - 6)² + 64.
Using the vertex form of the quadratic equation, we can say that the projectile reaches a maximum height of 64 meters after 6 seconds and the height of the cliff is 28 meters.
Hence, the equation can be written as follows:28 = a(0 - 6)² + 6428 = 36a + 6436a = - 36a = -1Therefore, the vertex form of the quadratic equation that represents the height, h, of the projectile after t seconds is given byy = -(x - 6)² + 64Answer: y = -(x - 6)² + 64.
Learn more on vertex here:
brainly.com/question/32432204
#SPJ11
pls ill give u brainly
Which equation represents the cross product equation derived from the proportion 6/x = 15/10?
Answers
Answer:
4
Step-by-step explanation:
Answer:
15x = 60
Step-by-step explanation:
Hope I helped!! :)..........................................Brainliest?