Breyelle is planning on purchasing a new sports-utility vehicle. The list price of the one she is most interested in buying is $32,000. This vehicle is expected to depreciate in value by 8.5% per year.
Which model could be used to calculate the daily depreciation for this vehicle?
V(t)=32,000(0.0233)^t
V(t)=32,000(0.9150)^t
V(t)=32,000(0.9767)t^t
V(t)=32,000(0.9998)^t
Answers
Answer:
V(t)=32,000(0.9767)t^t
Step-by-step explanation:
The correct model which could be used to calculate the daily depreciation for this vehicle is,
⇒ V (n) = 32,000 (0.915)ⁿ
What is mean by Subtraction?Subtraction in mathematics means that is taking something away from a group or number of objects. When you subtract, what is left in the group becomes less.
We have to given that;
Breyelle is planning on purchasing a new sports-utility vehicle.
Here, The list price of the one she is most interested in buying is $32,000.
And, This vehicle is expected to depreciate in value by 8.5% per year.
Hence, the daily depreciation for this vehicle is,
V (n) = 32,000 (1 - 8.5%)ⁿ
V (n) = 32,000 (1 - 0.085)ⁿ
V (n) = 32,000 (0.915)ⁿ
Thus, The correct model which could be used to calculate the daily depreciation for this vehicle is,
⇒ V (n) = 32,000 (0.915)ⁿ
Learn more about the subtraction visit:
https://brainly.com/question/17301989
#SPJ3
Related Questions
Help please with this bath problem the picture above

Answers
Answer:
a relation that is a function
Step-by-step explanation:
The Riemann zeta function for real numbers is defined for all x for which the series below converges. Find the domain of the function. (Enter your answer using interval notation.) ζ(x)=[infinity]∑n=1 n −x
Answers
The domain of the Riemann zeta function, denoted by ζ(x), is the set of real numbers x for which the series ∑n=1 ∞ n^(-x) converges. The domain of the function can be expressed using interval notation as (-∞, 1).
To understand the domain of the Riemann zeta function, we need to consider the convergence of the series ∑n=1 ∞ n^(-x). The series converges when the real part of x is greater than 1. Therefore, the right half-plane Re(x) > 1 represents a region where the series converges.
On the other hand, when the real part of x is less than or equal to 1, the series diverges. This means that the left half-plane Re(x) ≤ 1 is excluded from the domain of the Riemann zeta function.
Combining these conditions, we find that the domain of the Riemann zeta function is (-∞, 1) in interval notation, indicating that the function is defined for all real numbers less than 1.
To learn more about Riemann zeta function click here : brainly.com/question/31628401
#SPJ11
109. Effect of Gravity on Earth If a rock falls from a height of 20 meters on Earth, the height H (in meters) after r seconds is approximately H(x) = 20 - 4.9r? (a) What is the height of the rock when x = 1 second? When r = 1.1 seconqds? When x = 1.2 seconds? (b) When is the height of the rock 15 meters? When is it 10 meters? When is it 5 meters? (c) When does the rock strike the ground?
Answers
We have the expression for the height H of the rock in function of the time r, when it falls from a height of 20 meters:
\(H(r)=20-4.9\cdot r^2\)When r = 1 second, we have:
\(H(1)=20-4.9(1)^2=20-4.9\cdot1=20-4.9=15.1\)When r = 1.1 seconds, we have:
\(H(1.1)=20-4.9(1.1)^2=20-4.9\cdot1.21=20-5.929=14.071\approx14\)When r = 1.2 seconds, we have:
\(H(1.2)=20-4.9(1.2)^2=20-4.9\cdot1.44=20-7.056=12.944\approx13\)To know the time for each height, we have to work with the equation like this:
\(\begin{gathered} H=20-4.9r^2 \\ 4.9r^2=20-H \\ r^2=\frac{20-H}{4.9} \\ r=\sqrt{\frac{20-H}{4.9}} \end{gathered}\)Then, we can calculate at which time the height is 15 meters:
\(r=\sqrt{\frac{20-15}{4.9}=\sqrt{\frac{5}{4.9}}}=\sqrt{1.02}\approx1.01\)When the height is 10 meters, r is:
\(r=\sqrt{\frac{20-10}{4.9}=\sqrt{\frac{10}{4.9}=}}\sqrt{2.04}\approx1.43\)When the height is 5 meters, r is:
\(r=\sqrt{\frac{20-5}{4.9}=\sqrt{\frac{15}{4.9}=}}\sqrt{3.06}\approx1.75\)The rock hits the ground when H=0. This happens when r is:
\(r=\sqrt{\frac{20-0}{4.9}=\sqrt{\frac{20}{4.9}=}}\sqrt{4.08}\approx2.02\)A school changed their playground from a square shape into a rectangle to accommodate the remodel of the gymnasium. They added 50 feet to one side of the playground and decreased the other side by 20 feet. (A) Write an expression that could be used to express the area of the new playground. (B) Evaluate the expression assuming the original playground has the given side lengths: 50 ft, 100 ft, and 150ft. (C) Do you think there will ever be a time when the new playground will not have a larger area than the old playground? Explain your reasoning.
Answers
The expression of the area is A(x) = (x + 50)(x - 20)
The expression of the areaWe have
Side length of square = x
When modified, we have the dimension to be
x + 50 by x - 20
So, the area is
A(x) = (x + 50)(x - 20)
Evaluating the areas for the side lengthsHere, we have
A(50) = (50 + 50)(50 - 20) = 3000
A(100) = (100 + 50)(100 - 20) = 12000
A(150) = (150 + 50)(150 - 20) = 26000
The conclusion about te areaThe original playground was already the largest possible square, then the new rectangle will always have a smaller area than the original square.
Read more about areas at
https://brainly.com/question/22972014
#SPJ1
use the diagram below to find the measurements of angle abc

Answers
Answer :
55°
Detailed explanation:
The triangles are isosceles (having two sides of equal length and angle).
Hence solve for angle DCE
Angle DCE= 180°-(55°+55°)
=70°
As vertically opposite angles are equal. Thus,
angle ACB=70°.
Hence 180°-70°=110°
As the angles in an isosceles triangle are equal hence;
110°÷2=55°
Hence angle ABC is 55°
Hope this is has been clearly explained!
The measure of angle ABC from the given figure is 55 degree. Therefore, the correct answer is option A.
From the given figure, we have two isosceles triangles DCE and ABC.
In ΔDCE,
Base angle is ∠CED=55°.
Here, base angles are equal
That is, ∠CED=∠CED=55°
By using angle sum property of a triangle, we get
∠DCE=180°-(55°+55°)
∠DCE=70°
Now, ∠DCE and ∠ACB are vertically opposite angles are equal.
So, ∠DCE =∠ACB=70°
In ΔABC, base angles BAC and ABC are equal
So, ∠BAC+∠ABC+∠ACB=180°
∠ABC+∠ABC+70°=180°
2∠ABC=110°
∠ABC=55°
Therefore, the correct answer is option A.
To learn more about the angle sum property of a triangle visit:
https://brainly.com/question/8492819.
#SPJ4
1. A concert venue has 20 seats in the first row and an 5 additional seats in each successive row. If there are 35 rows of seats then how many people can attend a sold-out show?
A. 7,350 people
B. 2,100 people
C. 3,675 people
D. 190 people
Answers
7,350 people can attend a sold-out show at the concert venue with 20 seats in the first row and 5 additional seats in each successive row with a total of 35 rows of seats.
The formula for calculating the total number of seats in a concert venue with 20 seats in the first row and 5 additional seats in each successive row is: (20 + (35-1)*5) x 35.
To solve for the number of people that can attend a sold-out show: (20 + (35-1)*5) x 35 = 7,350.
7,350 people can attend a sold-out show at the concert venue with 20 seats in the first row and 5 additional seats in each successive row with a total of 35 rows of seats.
Therefore, 7,350 people can attend a sold-out show at the concert venue with 20 seats in the first row and 5 additional seats in each successive row with a total of 35 rows of seats.
Learn more about successive row here:
https://brainly.com/question/18830558
#SPJ4
Due in an hour help me
Please I have to pass




Answers
Answer:
A is answer
Step-by-step explanation:
Homework 4: Problem 11 Previous Problem Problem List Next Problem (1 point) Find k such that x(t) = 5¹ is a solution of the dx differential equation - = kx. dt k = Homework 4: Problem 12 Previous Problem Problem List Next Problem (1 point) Find the solution of the differential equation that satisfies the given initial condition. dy = :5y, y(0) = -3 dx y(x) = Homework 4: Problem 13 Previous Problem Problem List Next Problem (1 point) Find the solution of the differential equation that satisfies the given initial condition. dx 4 - x(0) = 5 dt x(t) = || X "
Answers
Problem 11: k = 1, Problem 12: y(x) = -3e^(-5x) and Problem 13: x(t) = 5t + 5, We can solve this differential equation using separation of variables.
Problem 11: We are given that x(t) = 5t is a solution of the differential equation -dx/dt = kx. We can substitute this into the differential equation to get -5 = kt. Solving for k, we find that k = -1/5.
Problem 12: We are given the differential equation dy/dx = 5y and the initial condition y(0) = -3. We can solve this differential equation using separation of variables.
The general solution is y = C*e^(5x), where C is an arbitrary constant. We can use the initial condition to find C = -3, so the specific solution is y(x) = -3e^(-5x).
Problem 13: We are given the differential equation dx/dt = 4 - x and the initial condition x(0) = 5. We can solve this differential equation using separation of variables.
The general solution is x = 4t + C, where C is an arbitrary constant. We can use the initial condition to find C = 5, so the specific solution is x(t) = 5t + 5.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
A grocery store has a sale on apples. Shoppers can buy 3 bags of apples for $5. Each bag contains 6 apples. Which of the following statements is true?

Answers
Answer:
i dont know
Step-by-step explanation:
Answer:
D.
Step-by-step explanation:
3b = 5$
3b = 6a
3b = 3 bags
6a = 6 apples
A. It costs 3.60 for 1 bag of apples
3.60 + 3.60 = 60 + 60 = 120 + 3 = 123 + 3 = 126
Meaning it would cost 126 for 3 bags of apples making this a incorrect option
B. It costs 3.60 for 1 apple
B is wrong because its one apple and if we were to subtract the apple would probably only cost a few change not 3$ and 60 cents.
C. The cost of 9 bags of apples is 30$
9b = 21a, its either c or d but I'm pretty sure its D!
D. The cost of 108 apples is 30$
D is correct
~ LadyBrain
Find the average rate of change between n = 2 and n = 4. (6 points) Question 10 options: 1) negative one fourth 2) one fourth 3) −4 4) 4


Answers
Answer:
-4
Step-by-step explanation:
From the graph:
When n=2 , a^n =9
When n=4, a^n =1
The average rate of change between n=2 and n=4 is :
\(Rate= \frac{{{a_{2} -a_{4} } } }{2-4} \\=\frac{9-1}{-2} \\=-4\\\)
The average rate of change is -4
PLEASE MARK ME AS BRAINLIEST
please help me with these questions
Problem 1: Find the measure of each marked angle. 2. (7x+19) (2x-1)º "V Vest (-3x+5)° (-8x+30) 5. 6. (32-2x)" (10x-10) (2x+18) (8x+14) (12x+40) (20x + 10) mand n are parallel. Problem 2: Identify th
Answers
In Problem 1, the measure of each marked angle is as follows:292º, -112º, -282º, -46º, 380º, 96º, 326º, 508º, and 790º.In Problem 2, the angles indicated by the letters in the given figure are as follows:c = 65º, d = 95º, e = 65º, f = 95º, g = 85º, and h = 85º.
Problem 1:The measures of the marked angles are as follows:(7x + 19)º and (-3x + 5)º are supplementary angles since they are the interior angles on the same side of the transversal "V Vest".
Therefore, we can say: (7x + 19)º + (-3x + 5)º = 180º Simplifying, 7x + 19 - 3x + 5 = 180
Combine like terms and solve for x: 4x + 24 = 180 4x = 180 - 24 4x = 156 x = 39 Now substitute x = 39 in the given expressions and find the value of each angle.
(7x + 19)º = (7 × 39 + 19)º = 292º(-3x + 5)º
= (-3 × 39 + 5)º = -112º(-8x + 30)º = (-8 × 39 + 30)º
= -282º(32 - 2x)º = (32 - 2 × 39)º = -46º(10x - 10)º
= (10 × 39 - 10)º = 380º(2x + 18)º = (2 × 39 + 18)º = 96º(8x + 14)º
= (8 × 39 + 14)º = 326º(12x + 40)º = (12 × 39 + 40)º
= 508º(20x + 10)º = (20 × 39 + 10)º = 790º
Therefore, the measures of the marked angles are:292º, -112º, -282º, -46º, 380º, 96º, 326º, 508º, and 790º.Problem 2:The angles indicated by the letters in the given figure are as follows: Angle c: Corresponding angles with respect to the parallel lines n and m are equal. Therefore, we can say: c = 65º.Angle d: Vertically opposite angles are equal. Therefore, we can say: d = 95º.
Angle e: Alternate interior angles with respect to the parallel lines n and m are equal. Therefore, we can say: e = 65º.Angle f: Corresponding angles with respect to the parallel lines n and m are equal. Therefore, we can say: f = 95º.Angle g: Interior angles on the same side of the transversal are supplementary. Therefore, we can say: g = 180º - 95º = 85º.Angle h: Vertically opposite angles are equal. Therefore, we can say: h = 85º.
To know more about angle visit:-
https://brainly.com/question/31818999
#SPJ11
Plz help me with this. Zack needs 5 3/4 cups of sugar to make cookies. He needs and additional 1 1/4 cup for bread. Find the total amount of sugar that zack needs
Answers
Answer:
7
Step-by-step explanation:
5 3/4 = 5.75
1 1/4 = 1.25
5.75 + 1.25 = 7.00
write the ratio 4.5: 2.25 in the form n:1
Answers
Step-by-step explanation:
you will divide both sides of the ratio I.e the 4.5 and 2.25 by 2.25

Your sports drink bottle is 56 full. After practice, the bottle is 38 full. Write the difference of the amounts after practice and before practice. Write your answer as a fraction in simplest form.
Answers
The difference of the amounts after practice and before practice is 18 full.
The difference as a fraction in simplest form will be 9/28.
How to calculate the value?The sports drink bottle is 56 full and after practice, the bottle is 38 full, the difference of the amounts after practice and before practice will be:
= 56 - 38
= 18
The difference as a fraction in simplest form will be:
= Difference / Original value
= 18 / 56
= 9 / 28
Learn more about fractions on:
brainly.com/question/17220365
#SPJ1
let f (x) = 9sin(x) for 0 ≤ x ≤ 2 . find lf (p) and uf (p) (to the nearest thousandth) for f and the partition p = 0, 6 , 4 , 3 , 2 .
Answers
The lower sum is 1.357 and the upper sum is 7.699.
How to find lf(p) and uf(p) for f with partition p?To find the lower sum, we need to evaluate f(x) at the left endpoint of each subinterval and multiply by the width of each subinterval:
L(f, P) = [(6-0) x f(0)] + [(4-6) x f(6)] + [(3-4) x f(4)] + [(2-3) x f(3)] + [(2-0) x f(2)] = [(6-0) x 0] + [(4-6) x 0.994] + [(3-4) x 0.951] + [(2-3) x 0.141] + [(2-0) x 0.412] = 0.412
To find the upper sum, we need to evaluate f(x) at the right endpoint of each subinterval and multiply by the width of each subinterval:
U(f, P) = [(6-0) x f(6)] + [(4-6) x f(4)] + [(3-4) x f(3)] + [(2-3) x f(2)] + [(2-0) x f(2)] = [(6-0) x 0.994] + [(4-6) x 0.951] + [(3-4) x 0.141] + [(2-3) x 0.412] + [(2-0) x 0.412] = 3.764
Therefore, the lower sum is approximately 0.412 and the upper sum is approximately 3.764.
Learn more about subinterval
brainly.com/question/31259780
#SPJ11
Help for brainliest.

Answers
Answer:
160 hope this work!!! love
help me plzzzzzzzzzzzzzzzzz

Answers
Answer:
The answer is D
Step-by-step explanation:
Answer:
(1,3,5,7,9)
U need to select the answer with the set of odd numbers.
You should know that if you skip every other one digit counting from 0 and infinite they are even and if you kip every other one digit counting from 1 and infinite those not skipped will be odds
Patrick can paint a house by himself in
t
+
4
hours. Karen can paint the same house by herself in
t
+
9
hours. If they work together, they can paint the house in
t
hours. How much time will it take for Patrick to paint the house by himself?
Answers
Answer:
Its 12
Step-by-step explanation:
Ok done
The point P = (-5/3 squared, y) lies on the unit circle shown below. What is the value of
y in simplest form?

Answers
The required value of y for the unit circle is: 2/3
How to find the point on the unit circle ?The circle is defined as the locus of a point whose distance from a fixed point is constant i.e center (h, k).
The equation of the circle is given by:
(x - h)² + (y - k)² = r²
where:
h, k is the coordinate of the center of the circle on coordinate plane.
r is the radius of the circle.
Here,
Equation of the unit circle is given as,
x² + y² = 1
Now substitute the given value in the equation,
5/9 + y² = 1
y² = 1 - 5/9
y² = 4/ 9
y = √(4/9)
y = 2/3
Thus, the required value of y for the unit circle is 2/3
Read more about Unit Circle at: https://brainly.com/question/26284611
#SPJ1
Red is spun on a spinner with five equal-size sections labeled red, yellow, blue, green, and purple. What is the probability of the complement of the event? Express your answer as a decimal.
Answers
The probability of the complement of spunning a red is 4/5.
What is probability?It is the chance of an event to occur from a total number of outcomes.
The formula for probability is given as:
Probability = Number of required events / Total number of outcomes.
We have,
Number of sections = 5
The probability of spunning a red.
= 1/5
The probability of the complement of spunning a red.
= 1 - 1/5
= 4/5
Thus,
4/5 is the probability of the complement of spunning a red.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ9
Ali is planning a cookout for family and friends. There will be 24 people at her cookout. Ali is renting tables for the cookout and wants to seat an equal number of people at each table. She needs to decide how many tables to get. How could she arrange the seating so that a reasonable and equal number of people sit at each table? Explain
PLS HELP
Answers
Answer:
6 or 4
Step-by-step explanation:
put 4 on each table which means you need 6 tables
or
put 6 on each table which means you need 4 tables
Step-by-step explanation:
oufhoqwufhqwlufhwughw
how many ways can you distribute 6 faceless players over 4 servers (each of the servers are identical)?
Answers
Therefore, there are 4 x 1128 = 4512 possible 5 card poker hands with at least 3 aces that can be dealt from a standard deck of 52 cards.
1. There are 4 aces in a standard deck of 52 cards, so the maximum number of aces in a 5-card poker hand is 3.
2. There are C(4,3) = 4 ways to choose 3 aces out of the 4 aces in the deck.
3. For the remaining 2 cards, there are C(48,2) = 1128 ways to choose them from the 48 non-ace cards.
4. Therefore, there are 4 x 1128 = 4512 possible 5 card poker hands with at least 3 aces that can be dealt from a standard deck of 52 cards.
There are 4 aces in a standard deck of 52 cards, so the maximum number of aces in a 5-card poker hand is 3. There are C(4,3) = 4 ways to choose 3 aces out of the 4 aces in the deck. For the remaining 2 cards, there are C(48,2) = 1128 ways to choose them from the 48 non-ace cards.
Learn more about cards here
https://brainly.com/question/29862517
#SPJ4
m 1 = a) 40 b) 130 c)50

Answers
Answer:
C) 50
Step-by-step explanation:
You first look at the 40 given to you. Then you know the angle opposite of it will be 40 also because of the law that opposite angles are the same. Once you have two angles in the triangle you can add 40 plus 90 in which you get 130 but that does not equal 180. So you can see that angle 1 is 50 because 50 and 130 equals 180.
PLEASE HELP ASAP :D
what is
sin
cos
tan
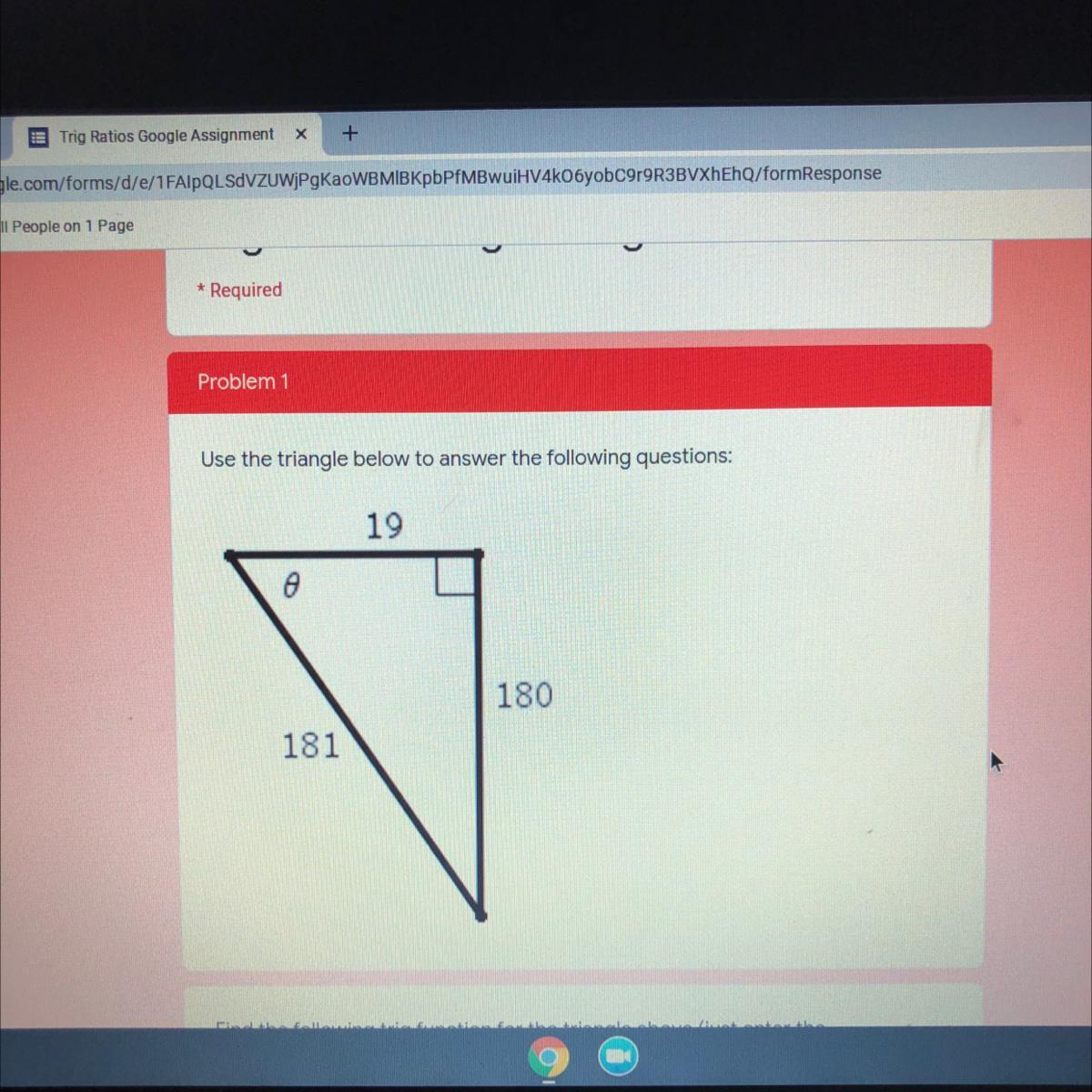
Answers
Answer:
sin=180/181
cos=19/181
tan=19/180
How many degrees of freedom does the chi-square test statistic for a goodness of fit have when there are 10 categories?.
Answers
Degree of freedom for chi-square test for 10 categories will be 9.
What is chi- square test?
A test that evaluates how well a model matches real observed data is that the chi-square (χ²) statistic. A chi-square statistic can only be calculated with data that's random, unprocessed, mutually exclusive, obtained from independent variables, and drawn from a large enough sample.
The Formula for Chi-Square Is
χ(c)=²∑(Oₐ-Eₐ)₂/Eₐ²
where:
c=Degrees of freedom
O=Observed value(s)
E=Expected value(s)
Main Body:
Degree of freedom = total categories -1
so no. of categories= 10
Degree of freedom = 10 - 1
Hence degree of freedom = 9
To learn more about chi- square test click on the link below
https://brainly.com/question/4543358
#SPJ4
what is a distributive property of 7 x 6
also pls make it simple
Answers
Answer:
The distributive property helps us to rewrite the expression and to get the same answer. The rule is: a * ( b + c ) = a * b + a * c. In this case: 7 * 6 = 7 * ( 3 + 3 ) = 7 * 3 + 7 * 3 = 21 + 21 = 42. And also : 7 * 6 = 42. We can use it also like this: 7 * 6 = 7 * ( 5 + 1 ) = 7 * 5 + 7 * 1 = 35 + 7 = 42, etc.Hope this helps. Let me know if you need additional help!
7(6)
If you would like an explanation, then it's pretty much simple so... please just ask.
find the missing values in the ratio table
please show explanation

Answers
Answer:
0.6, 1.2, 1.8, 2.4
1, 2, 3, 4
Step-by-step explanation:
The Spearman rank-order correlation coefficient is a measure of the direction and strength of the linear relationship between two ______ variables.
a.
nominal
b.
interval
c.
ordinal
d.
ratio
Answers
The Spearman rank-order correlation coefficient is a measure of the direction and strength of the linear relationship between two ordinal variables.
Spearman's rank-order correlation is used when two variables are measured on an ordinal scale.
What is the Spearman Rank-Order Correlation Coefficient?
The Spearman Rank-Order Correlation Coefficient is a non-parametric statistical measure that estimates the relationship between two variables using ordinal data.
It evaluates the strength and direction of a relationship between two variables by rank-ordering the data.
The Spearman correlation coefficient, named after Charles Spearman, calculates the association between two variables' rankings.
The correlation coefficient ranges from -1 to +1. A value of +1 indicates that there is a perfect positive relationship between the variables, whereas a value of -1 indicates that there is a perfect negative relationship between the variables.
In contrast, a value of 0 indicates that there is no correlation between the variables.
To learn more about Spearman rank-order correlation coefficient :
https://brainly.com/question/31502090
#SPJ11
For the following functions, a. use Equation 3.4 to find the slope of the tangent line m tan=f ′(a), and b. find the equation of the tangent line to f at x=a. 15. f(x)= x7,a=3
Answers
(a) The slope of the tangent line m tan = 510. (b) Equation of the tangent line to f at x=aLet m tan = 5103, x = 3, and y = f(3) = 37 = 2187. The equation of the tangent line to f at x = a is y = 5103x − 13122.
a. Slope of the tangent line m tan = f’(a)Let f(x) = x7 and a = 3f'(x) = 7x6 [Differentiate with respect to x]f'(a) = 7(3)6 = 7 × 729= 5103The slope of the tangent line m tan is equal to f’(a)Therefore, the slope of the tangent line m tan = 5103.b. Equation of the tangent line to f at x=aLet m tan = 5103, x = 3, and y = f(3) = 37 = 2187. Plug in the values in the point-slope equation of a line.y − y1 = m(x − x1)Therefore,y − 2187 = 5103(x − 3)Distribute 5103y − 2187 = 5103x − 15309Rearrange the equation to get it in slope-intercept form.y = 5103x − 13122The equation of the tangent line to f at x = a is y = 5103x − 13122.
Slope is one of the most concepts in mathematics. It is defined as the ratio of the change in the y-value of a function to the change in the x-value of the function. The slope of a function can be used to find the tangent line of the function at a specific point. A tangent line is a line that touches the curve of the function at a single point. The slope of the tangent line at that point is equal to the slope of the function at that point.There are different ways to find the slope of the tangent line of a function. One of the methods is to use the derivative of the function.
The derivative of a function is the rate at which the function changes with respect to its input. The derivative of a function is also the slope of the tangent line to the function at a given point. Equation 3.4 can be used to find the slope of the tangent line to a function at a given point.The equation of the tangent line to a function at a given point can be found using the point-slope equation of a line. The point-slope equation of a line is y − y1 = m(x − x1), where m is the slope of the line and (x1, y1) is a point on the line. To find the equation of the tangent line to a function at a given point, the slope of the tangent line and a point on the line must be known.
To know more about tangent visit :
https://brainly.com/question/10053881
#SPJ11
Marc decided to place $453 in equal deposits every month at the beginning of the month into a savings account earning 7.29 percent per year, compounded monthly for the next 11 years. The first deposit is made today. How much money will be on his account at the end of that time period?
Answers
After making equal monthly deposits of $453 for 11 years into a savings account earning 7.29 percent interest compounded monthly, Marc will have approximately $89,909.92 in his account.
To calculate the total amount of money in Marc's account at the end of 11 years, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A is the final amount in the account,
P is the monthly deposit amount,
r is the annual interest rate (expressed as a decimal),
n is the number of times the interest is compounded per year, and
t is the number of years.
In this case, Marc makes monthly deposits of $453, the annual interest rate is 7.29 percent (0.0729 as a decimal), and the interest is compounded monthly (n = 12). The number of years is 11.
Using the formula, we can calculate the final amount:
A = 453(1 + 0.0729/12)^(12*11)
A ≈ 89,909.92
Therefore, at the end of 11 years, Marc will have approximately $89,909.92 in his savings account.
Learn more about compound interest here:
https://brainly.com/question/14295570
#SPJ11