Caitlin is designing a railing for a set of stairs. The railing will begin at a height of 36 inches and follow the slant of the stairs, which decreases 9 inches for every 12 horizontal inches. Which function can represent the height, y, of the railing in inches according to the horizontal distance in inches, x, from the top of the stairs? Y = –StartFraction 3 Over 4 EndFractionx + 36 y = –3x + 36 y = StartFraction 3 Over 4 EndFractionx + 36 y = 3x + 36

Answer:

the correct answer is B

Step-by-step explanation:

HAVE A GREAT DAY!

The correct answer is B.

An equation is an identity if it can be rewritten as 0=0. Such an equation has an infinite number of solutions because it reduces to a true statement regardless of the value of the variable.

An equation is a mathematical statement which is true only for some set of values.

An identify is a mathematical statement which is true only for all the values.

Here, only option B "An equation is an identity if it can be rewritten as 0=0. Such an equation has an infinite number of solutions because it reduces to a true statement regardless of the value of the variable." satisfies the condition.

So, option B is correct.

Learn more about equation and identity here:

https://brainly.com/question/1675364?referrer=searchResults

Answer:

113.1 cm³

Step-by-step explanation:

diameter = 2 X radius

Volume of sphere = (4/3) X π X r ³

= (4/3) π (3)³

= 36π

= 113.1 cm³ to nearest tenth

Answer:

Awnser is C

Step-by-step explanation:

We just have to make the top bar seem bigger then it actually is

(a) The dot product of A and B is given by: A · B = (2î + 3ĵ + 4k) · (î - 2ĵ + 3k)= 2(1) + 3(-2) + 4(3)= 2 - 6 + 12 = 8

Therefore, A · B = 8.

(b) The angle between two vectors A and B is given by:

θ = cos^(-1)((A · B) / (|A| |B|))

In this case, |A| is the magnitude of vector A and |B| is the magnitude of vector B. The magnitude of a vector is given by the square root of the sum of the squares of its components.

|A| = √(2² + 3² + 4²) = √(4 + 9 + 16) = √29

|B| = √(1² + (-2)² + 3²) = √(1 + 4 + 9) = √14

Plugging in the values:

θ = cos^(-1)(8 / (√29 √14))

(c) The scalar component of vector A in the direction of vector B is given by:

A_B = (A · B) / |B|

Plugging in the values:

A_B = 8 / √14

(d) The cross product of vectors A and B is given by:

A x B = (2î + 3ĵ + 4k) x (î - 2ĵ + 3k)

= (3(3) - 4(-2))î + (4(1) - 2(3))ĵ + (2(-2) - 3(3))k

= 17î - 2ĵ - 13k

Therefore,AXB = 17î - 2ĵ - 13k.

Learn more about Dot Product here -: brainly.com/question/30404163

#SPJ11

(a) The dot product of A and B is given by: A · B = (2î + 3ĵ + 4k) · (î - 2ĵ + 3k)= 2(1) + 3(-2) + 4(3)= 2 - 6 + 12 = 8

Therefore, A · B = 8.

(b) The angle between two vectors A and B is given by:

θ = cos^(-1)((A · B) / (|A| |B|))

In this case, |A| is the magnitude of vector A and |B| is the magnitude of vector B. The magnitude of a vector is given by the square root of the sum of the squares of its components.

|A| = √(2² + 3² + 4²) = √(4 + 9 + 16) = √29

|B| = √(1² + (-2)² + 3²) = √(1 + 4 + 9) = √14

Plugging in the values:

θ = cos^(-1)(8 / (√29 √14))

(c) The scalar component of vector A in the direction of vector B is given by:

A_B = (A · B) / |B|

Plugging in the values:

A_B = 8 / √14

(d) The cross product of vectors A and B is given by:

A x B = (2î + 3ĵ + 4k) x (î - 2ĵ + 3k)

= (3(3) - 4(-2))î + (4(1) - 2(3))ĵ + (2(-2) - 3(3))k

= 17î - 2ĵ - 13k

Therefore,AXB = 17î - 2ĵ - 13k.

Learn more about Dot Product here -: brainly.com/question/30404163

#SPJ11

Answer:

ok and?

Step-by-step explanation:

After 10 hours the two companies costs the same as per the given information in the question.

The phrase linear function relates to two distinct but related concepts in mathematics:

Some authors use the term "linear function" only for linear mappings that accept values in the scalar field; these are more frequently known as linear forms.

Calculus' "linear functions" qualify as "linear mappings" when (and only when) f(0,..., 0) = 0, or, equivalently, when the aforementioned constant b equals zero.

A linear function is also known as a linear map in linear algebra, mathematical analysis, and functional analysis.

The costs for company A=50+10x

The costs for company B=70+8X

Where x=time in hours

Given,

A) 50+10x=70+8x

2x=20

x=10

After 10 hours the two companies costs the same.

To know more about linear equation, visit:

https://brainly.com/question/20286983

#SPJ9

The possible dimensions (length and width) of the field are:(10 m × 13 m) or (13 m × 10 m) and (11 m × 12 m) or (12 m × 11 m).

Given that Aaron has 47m of fencing to build a three-sided fence around a rectangular plot of land that sits on a riverbank. The fourth side of the enclosure would be the river.

The area of the land is 266 square meters.To find the possible dimensions (length and width) of the field, we can use the given information.The length of fencing required = 47 m.

Since the fence needs to be built on three sides of the rectangular plot, the total length of the sides would be 2l + w = 47.1. When l = 10 and w = 13, we have:

Length of the field, l = 10 m Width of the field, w = 13 mArea of the field = l × w = 10 × 13 = 130 sq. m2. When l = 11 and w = 12,

we have:Length of the field, l = 11 m

Width of the field, w = 12 m

Area of the field = l × w = 11 × 12 = 132 sq. m

To learn more about :  dimensions

https://brainly.com/question/28107004

#SPJ8

Answer:

V = 340.339

Step-by-step explanation:

V = \(\frac{\pi r^{2} h }{3}\)

V = \(\pi\)\((5)^{2}\) \(\frac{13}{3}\) = 25\(\pi\) \(\frac{13}{3}\)  = about 340.3392 = 340.339

Answer:

340.17 ft.

Step-by-step explanation:

Using the formula, πr²h ÷ 3 (3.14 × radius × radius × height ÷ 3), we can plug-in the unknown values.

'r' means radius; 'h' means height; 'π' means pi.

The radius is 5; the height is 13.

πr²h (3.14 × radius × radius × height ÷ 3) - π5² × 13 = 340.166666667 (3.14 × 5 × 5 × 13 ÷ 3 = 340.166666667)

340.166666667 ≈ 340.17

Therefore, the area of this circular cone is 340.17 ft.

The correct standard form for the given LP model is option C: Max(Z) = 3x1 + 2x2, subject to the constraints 11x1 + 3x2 - 5 <= 33, 8x1 + 5x2 + 5 >= 40, and 7x1 + 10x2 + 5 >= 70, with x1, x2 >= 0. This option aligns with the original objective function and constraints of the LP model.

To convert the LP model into standard form, we need to rewrite the constraints with the variables on the left-hand side and constants on the right-hand side, with inequality signs (<= or >=) consistent throughout. Additionally, we introduce slack or surplus variables to transform any non-standard constraints.

In option C, the constraints are correctly transformed as 11x1 + 3x2 - 5 = 33, 8x1 + 5x2 + 5 >= 40, and 7x1 + 10x2 + 5 >= 70. These constraints are consistent with the original model. The objective function remains the same, Max(Z) = 3x1 + 2x2.

Option A has incorrect signs in the transformed constraints, and option B introduces surplus variables (+5) instead of slack variables (-5), resulting in an incorrect standard form. Option D includes a non-standard term with a dollar sign, which is inconsistent with linear programming conventions.

Therefore, option C is the correct standard form, adhering to the original LP model's objective function and constraints.

Learn more about LP model here : brainly.com/question/33051152

#SPJ11

The factorize expression of 25x²-4x²-9 is 3(7x²-3).

Factorization is a process to simplify the expression by finding the factors of that expression.

And to find the same expression from factors, you have to reverse the process.

We have the quadratic function,

25x²-4x²-9.

To factorize the function:

First, combine similar terms,

25x²-4x²-9,

= 21x²-9.

Now, factor out the common factor.

That means,

3(7x²-3).

Therefore, the required function is 3(7x²-3).

To learn more about the factorization;

https://brainly.com/question/29474540

#SPJ1

The best definition of the test statistic is the number of standard errors above or below the expected outcome that our sample z-score corresponds to. In other words, the test statistic measures how far our sample mean deviates from the expected population mean in terms of standard deviation units.

The test statistic is a crucial element in hypothesis testing as it helps us determine the probability of obtaining our sample mean by chance. We use the test statistic to calculate the p-value, which is the probability of obtaining a result as extreme as our sample mean under the null hypothesis.

The boundary value corresponding to the p-value is determined by the level of significance we choose for our test. If our p-value is less than the level of significance (usually 0.05), we reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis.

In summary, the test statistic is a measure of how far our sample mean deviates from the expected population mean in standard deviation units. It is used to calculate the p-value and determine the level of significance for our hypothesis test.
The best definition of the test statistic among the given terms is: the number of standard errors above or below the expected outcome that our sample represents. A test statistic is a value calculated from sample data that is used to determine whether to reject or fail to reject a null hypothesis in hypothesis testing. It measures how far the sample statistic is from the hypothesized population parameter, considering the sample's variability.

In simpler terms, the test statistic helps us understand how likely our sample results are, given the null hypothesis. It does this by comparing the sample's outcome to what we would expect under the null hypothesis, considering the variability within the sample. By calculating the test statistic, we can then determine the corresponding p-value, which represents the probability of obtaining the observed results or more extreme results, assuming the null hypothesis is true.

In summary, the test statistic quantifies the difference between the sample outcome and the expected outcome under the null hypothesis, expressed in terms of the number of standard errors. It helps us make decisions about the null hypothesis based on the calculated p-value.

Learn more about z-score at: brainly.com/question/31871890

#SPJ11

No, we would not expect about 95% of the samples to have their variances within 0.008 of 0.009.

The variance of a normal distribution with mean μ and variance σ^2 is given by σ^2, which in this case is equal to (0.004)^2 = 0.000016.

The variance of the sample means, on the other hand, is given by σ^2/n, where n is the sample size. In order for about 95% of the samples to have variances within 0.008 of 0.009, we would need the sample size to be approximately equal to:

n ≈ σ^2 / (0.008 - 0.009)^2 = 62500

This means that we would need very large samples for this to be true. However, if the sample size is relatively small, then the distribution of sample means will not necessarily be normal and the Central Limit Theorem may not apply.

In that case, the distribution of sample variances will not necessarily follow the same pattern as the distribution of the population variance, and it may not be possible to make predictions about the sample variances based on the population parameters.

To learn more about mean click on,

https://brainly.com/question/30598523

#SPJ4

The product of the radical expressions √(4/7) and √(5/7) can be simplified as √(20/49).


To simplify the product of the radical expressions, we can multiply the individual expressions together. The given expressions are √(4/7) and √(5/7).

Multiplying these expressions, we have:

√(4/7) * √(5/7) = √((4/7) * (5/7)).

To simplify the expression further, we can multiply the numerators together and the denominators together:

√((4/7) * (5/7)) = √(20/49).

The expression √(20/49) can be simplified as follows:

√(20/49) = √(20)/√(49).

Since the square root of 49 is 7, we have:

√(20)/√(49) = √20/7.

However, the expression can be simplified further by simplifying the square root of 20. The square root of 20 can be broken down into √(4 * 5), which is equal to √4 * √5. Since √4 is 2, we have:

√20/7 = (2√5)/7.

Therefore, the product of the radical expressions √(4/7) and √(5/7) simplifies to (2√5)/7.

Learn more about product here : brainly.com/question/16941498

#SPJ11

Answer:

The simplest form of 108/648 is 16

For the given condition 108 as a fraction of 648 will be 108/648.

Fraction number consists of two parts, one is the top of the fraction number which is called the numerator and the second is the bottom of the fraction number which is called the denominator.

We have to write 108 as a fraction of 648, in simplified form.

p as the fraction of q in the simplified form can be written as,

=p/q

For the given condition we have to write the 108 as a fraction of 648 in the simplified form.

Write the fraction's numerator, hyphenate it, and then spell out the denominator to represent it verbally. The phrase p/q would be used to represent the fraction 108/648.

Thus, for the given condition 108 as a fraction of 648 will be 108/648.

Learn more about the fraction here:

brainly.com/question/1301963

#SPJ6

Sabric is correct because -3.613 is to the left of -3.63 on a number line.

To compare the values -3.613 and -3.63, we can plot them on a number line. The value -3.613 is closer to zero than -3.63, so it would be positioned to the left of -3.63. Therefore, Sabric's claim that -3.613 is greater than -3.63 is correct.

To visualize this, imagine a number line with zero in the middle and negative numbers extending to the left. Placing -3.613 and -3.63 on this number line, we can see that -3.613 is to the left of -3.63.

-4    -3.8   -3.6   -3.4   -3.2   -3   -2.8   -2.6   -2.4   -2.2   -2

 |----------|----------|----------|----------|----------|----------|

                   -3.613                    -3.63

As we can see, -3.613 lies to the left of -3.63 on the number line.

Jessica's claim that -3.613 is less than -3.63 is incorrect because it is the other way around. Sabric is correct in stating that -3.613 is greater than -3.63. It's important to note that when comparing numbers, their positions on the number line determine their relative values. In this case, -3.613 is to the left of -3.63, indicating that it is smaller or "less than" -3.63. Therefore, Sabric's claim is accurate.

Learn more about comparing : brainly.com/question/31877486

#SPJ11

In both the male and female versions of the Harris-Benedict Formula, the weight (lb) term affects the BMR the most due to its higher coefficient, indicating that changes in weight have a significant impact on the BMR calculation.

In the Harris-Benedict Formula, the BMR calculation includes multiple terms such as weight (lb), height (in.), and age (years). However, when determining which term affects the BMR the most, we need to consider the coefficients associated with each term.

For females, the BMR calculation includes the terms 4.35 times weight (lb), 4.7 times height (in.), and 4.7 times age (years). Among these terms, the weight term has a coefficient of 4.35, which is relatively larger than the coefficients of the other terms. This indicates that changes in weight have a stronger impact on the BMR calculation for females.

Similarly, for males, the BMR calculation includes the terms 6.23 times weight (lb), 12.7 times height (in.), and 6.8 times age (years). Here, the weight term also has a larger coefficient of 6.23, suggesting that variations in weight have a greater influence on the BMR calculation for males.

Learn more about coefficients here:

https://brainly.com/question/30524977

#SPJ11

Measuring length and width can determine if the center section is within specification. The given statement is insufficient to be determined as true or false as the statement doesn't specify the length and width of what is being measured.

Therefore, we can not provide the required answer without knowing the complete question. Hence, we need further information on the complete statement. In technical terms, specifications are a set of specifications and requirements that a product, materials, service, or system must meet. Specifications are developed to ensure that products, systems, or services are consistent, trustworthy, and meet the needs of the end-user. Therefore, specifications play a crucial role in ensuring the quality and reliability of a particular product or service. It also helps to determine whether a product or service meets the required safety and performance standards or not.

Learn more about length

https://brainly.com/question/32060888

#SPJ11

Answer:

10.  x=4/3 or 1.3

11. No solution

12. All real numbers

13. x=0

14. No solution

15. All real numbers

16. No solution

17. x=3/4 or 0.75

18. No solution

Step-by-step explanation:

Answer:

i think its -13/10

Step-by-step explanation:

Answer:

-13/10

Step-by-step explanation:

The FV is $107 for the simple interest.

The formula to calculate simple interest is given as:

I = P × R × T

Where,I is the simple interest, P is the principal or initial amount, R is the rate of interest per annum, T is the time duration.

Formula to find FV:

FV = P + I = P + (P × R × T)

where,P is the principal amount, R is the rate of interest, T is the time duration, FV is the future value.

Given that P = $100, R = 7%, and T = 1 year, we can find the FV of the investment:

FV = 100 + (100 × 7% × 1) = 100 + 7 = $107

Therefore, the FV of $100 invested at 7% for one year (simple interest) is $107.

#SPJ11

Let us know more about FV : https://brainly.com/question/27941044.

Answer:

  3.  · (times)

Step-by-step explanation:

You want to know the operation that will give a binomial result from the expressions (3y^6 +4) and (9y^12 -12y^6 +16).

The like terms in the two expressions are 3y^6 and -12y^6, or +4 and +16. Combining these terms by addition or subtraction will not result in the elimination of either the y^6 term or the constant term. Hence addition or subtraction cannot result in a binomial.

We know that the sum of cubes is factored into the product of a binomial and a trinomial:

  a³ +b³ = (a +b)(a² -ab +b²)

Comparing this form to the given binomial and trinomial, we see that we can choose ...

  a = 3y^6

  b = 4

to make the given factors match exactly. That tells us their product will be a binomial sum:

  (3y^6 +4) × (9y^12 -12y^6 +16) = (3y^6)^3 +(4)^3 = 27y^18 +64

The operation "times" (·) will result in a binomial.

Answer and Explanation:

Given:

Let's go ahead and chose different values of x and corresponding values of y;

When x = -2;

When x = -1;

When x = 0;

When x = 1;

When x = 5;

With the above values, we can go ahead and graph the function as seen below;

The domain of a function is the set of possible input values(x-values) for which the function is defined. On a graph, it is the set of x-values from left to right.

Looking at the given graph, we can see that the domain is;

The range of a function is the set of possible output values(y-values). It is the set of y-values from the bottom to the top of the graph.

Looking at the given graph, we can see that the range is;

Answer:

True

Step-by-step explanation:

Cos^-1   = 1/ cos = sec x

Answer: True

Step-by-step explanation:

     When the cos(ine) function is raised to the negative first power, we find the reciprocal. This will be the case for most functions and numbers.

If the research team continues to run laboratory tests, then the mean number of trials until failure is  8.06.

That a research team has developed a face recognition device to match photos in a database. From laboratory tests, the recognition accuracy is 89% and trials are assumed to be independent. We need to find out the mean number of trials until failure.

(a) Mean number of trials until failure

Using the binomial distribution formula, mean number of trials until failure is given by:

μ = (1 - p)/p

Where p is the probability of success, which is 89% or 0.89. Thus, q = 1 - p = 0.11Substituting the values in the formula, we get:

μ = (1 - 0.89) / 0.89 = 0.11 / 0.89 ≈ 0.124

Thus, the mean number of trials until failure is approximately 0.124 or 1/0.124 ≈ 8.06 trials. Therefore, the mean number of trials until failure is 8.06 trials (approx).

To learn more about mean: https://brainly.com/question/1136789

#SPJ11

Answer:

Refer to the attachment \(\Huge{\blue{\nearrow}}\)

Step-by-step explanation:

\(\setlength{\unitlength}{1.1mm}\begin{picture}(50,55)\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(1,3){6.4}}\put(25,30){\line(1, - 3){6.4}}\put(20,7){\line(3,1){68.5}}\put(20,52.8){\line(3, - 1){68.5}}\put(25,30){\circle*{1}}\put(88,30){\circle*{1.2}}\put(22,30){\sf O}\put(31,6){\sf A}\put(31,52){\sf B}\put(90,28.5){\sf P}\multiput(25,30)(3,0){21}{\line(2,0){1.8}}\qbezier(81.5,32)(78,30)(81,27.5)\qbezier(76,30)(74.5,28)(76,26)\put(33,45){\line(1,3){1.1}}\put(30,45.8){\line(3, - 1){3.2}}\put(30.5,14){\line(3,1){3.2}}\put(33.5,15){\line(1, - 3){1.1}}\put(21,18){\sf 6 cm}\put(73,30.8){\sf 120^\circ$}\put(69,26){\sf 60^\circ$}\end{picture}\)

View the ans from Web for complete diagram.

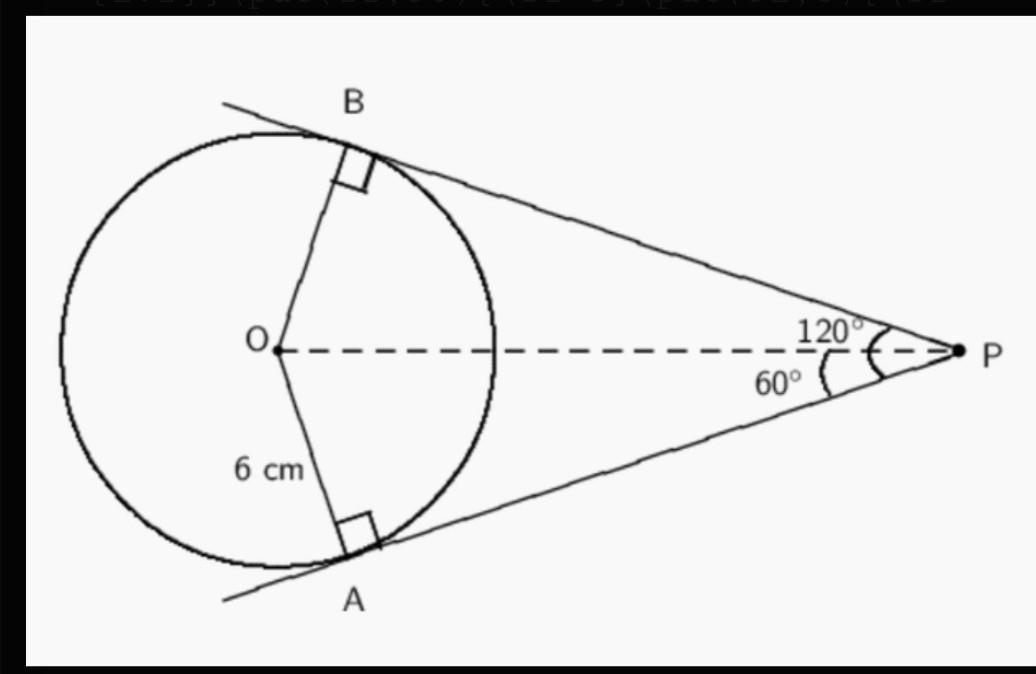
Answer:

I hate edge :l

Answer:

y = -11x - 13

Step-by-step explanation:

Step 1: Subtract 11x from both sides.

Therefore, the answer is y = -11x - 13.

During conventional Pavlovian conditioning, the conditional stimulus is repeatedly presented just before the unconditional stimulus.

In Pavlovian conditioning, the conditional stimulus (CS) and the unconditional stimulus (US) play crucial roles in shaping the learning process. The CS refers to a neutral stimulus that, through repeated pairing with the US, comes to evoke a conditioned response (CR) similar to the response elicited by the US. The US, on the other hand, is a stimulus that elicits an unconditioned response (UR) naturally and without prior learning. In the context of conventional Pavlovian conditioning, the CS is repeatedly presented just before the US. This temporal association allows the CS to become a reliable predictor of the US, leading to the formation of an association between the two stimuli. As a result, the CS acquires the ability to elicit a CR that resembles the UR evoked by the US. This process is often referred to as classical conditioning or associative learning, where the CS serves as a signal for the upcoming US and triggers the conditioned response.

Learn more about Pavlovian conditioning here:

https://brainly.com/question/30624921

#SPJ11

Based on the given information about Ravin's spending and saving habits, the true statement is "Ravin allocates $350 every two weeks as a store of value in his savings account.

Ravin gets paid $1000 every two weeks.

Every payday, the first thing he does is he immediately puts $350 in his savings account.

Using online bill pay through his bank, Ravin spends about $400 on bills such as his cell phone, electricity, and rent.

Ravin withdraws $150 in cash for daily expenses, and leaves the remaining amount ($100) in his checking account.

From the given information, we can see that Ravin saves $350 every two weeks in his savings account.

To know more about saving account visit

https://brainly.com/question/1446753

#SPJ11