can 18 in, 6 in, 13 in form a triangle
Answers
Answer:
can bcz triangle has 3 sides here 3 cm are there
Related Questions
Use the graph of the function,
f(x)=x-1/x^2+5x+6
to identify the function's
vertical asymptotes.
a. x=-1, x= 6
b. x=1, x=-6
c. x=-2, x=-3
d. X= 2, x= 3
Answers
Answer:
c. x = -2 or x = -3
Step-by-step explanation:
The vertical asymptotes occur where the denominator = 0. That happens when the f(x) is undefined. So,
x^2 + 5x + 6 = 0
(x + 2)(x + 3) = 0
x = -2 or x = -3
PLSSSS HELLLLLLLLLPPPPPPPPPPPPPPP

Answers
Answer:
24 cubes
Step-by-step explanation:
You can figure this a couple of ways.
I usually find it easiest to figure in terms of the number of cubes each dimension represents. The vertical dimension (3/2 cm) is the length of 3 cubes; the front-back dimension (2 cm) is the length of 4 cubes, and the width (1 cm) is the length of 2 cubes.
The total number of cubes required is the product of the dimensions in cube-lengths: 3×4×2 = 24 cubes.
- 3/4n+11-__=5-____ I don’t understand the problem

Answers
I think itś 11 on both sides bc positive and negative 11 would cancel out and then 5-11 would -6. if you look at the bottom question there is a negative 6 there too. if im wrong its mb.
Answer:
Step-by-step explanation:
\(-\frac{3}{4} n+11-11=5-11 ~subtract~11~from~both~sides\\-\frac{3}{4} n=-6\\multiply~both~sides~by ~-\frac{4}{3} \\(-\frac{3}{4} n)(-\frac{4}{3} )=(-6)(-\frac{4}{3} )\\n=8\)
What is the sum of the interior angles of this polygon?

Answers
Answer:
\(D.\ 720\ degrees\)
Step-by-step explanation:
\(We\ are\ given:\\The\ following\ polygon\ has\ 6\ sides\ and\ is\ a\ hexagon.\\We\ know\ that,\\The\ Interior\ Angle\ Sum\ of\ a\ polygon\ with\ sides\ n\ is\ given\ by\ the\ formula:\\Interior\ Angle\ Sum=180(n-2)\\Here,\\As\ the\ number\ of\ sides\ are\ 6,n=6\\Hence,\\The\ Interior\ Angle\ Sum\ of\ a\ hexagon=180(6-2)=180*4=720\)
John wishes to choose a combination of two types of cereals for breakfast - Cereal A and Cereal B. A small box (one serving) of Cereal A costs $0.50 and contains 10 units of vitamins, 5 units of minerals, and 15 calories. A small box (one serving) of Cereal B costs $0.40 and contains 5 units of vitamins, 10 units of minerals, and 15 calories. John wants to buy enough boxes to have at least 500 units of vitamins, 600 units of minerals, and 1200 calories. How many boxes of each cereal should he buy to minimize his cost?
Answers
Let's assume that John buys x boxes of Cereal A and y boxes of Cereal B. Then, we can write the following system of inequalities based on the nutrient and calorie requirements:
10x + 5y ≥ 500 (minimum 500 units of vitamins)
5x + 10y ≥ 600 (minimum 600 units of minerals)
15x + 15y ≥ 1200 (minimum 1200 calories)
We want to minimize the cost, which is given by:
0.5x + 0.4y
This is a linear programming problem, which we can solve using a graphical method. First, we can rewrite the inequalities as equations:
10x + 5y = 500
5x + 10y = 600
15x + 15y = 1200
Then, we can plot these lines on a graph and shade the feasible region (i.e., the region that satisfies all three inequalities). The feasible region is the area below the lines and to the right of the y-axis.
Next, we can calculate the value of the cost function at each corner point of the feasible region:
Corner point A: (20, 40) -> Cost = 20
Corner point B: (40, 25) -> Cost = 25
Corner point C: (60, 0) -> Cost = 30
Therefore, the minimum cost is $20, which occurs when John buys 20 boxes of Cereal A and 40 boxes of Cereal B.
Probability of rolling a 2 or an odd number
Answers
Answer:
When rolling di.e #2, since we must roll a different odd number, the probability of doing so is 2/6 = 1/3. Thus, the probability is 1/2 x 1/3 = 1/6.
Probability (E)= Number of favourable outcome/Total number of outcomes
=4/6
=2/3
Cost of a puppy: $349.99
Discount: 23%
What is the new cost?
Answers
Answer:
$269.49
Step-by-step explanation:
Discount = Original Price x Discount %/100
Discount = 349.99 × 23/100
Discount = 349.99 x 0.23
You save = $80.50
Final Price = Original Price - Discount
Final Price = 349.99 - 80.4977
Final Price = $269.49
Fill in the table 'using this function rule.
y = -5x+2
x
-1
0
1
2
y
0
0
0
X
4
S

Answers
Answer:
7, 2, -3, -8
Step-by-step explanation:
y = -5x + 2 Substitute in -1 for x
y = -5(-1) + 2
y = 5 + 2
y = 7
y = -5x + 2 Substitute in 0 for x
y = -5(0) + 2
y = 0 + 2
y = 2
y = -5 + 2 substitutes in 1 for x
y = -5(1) + 2
y = -5 + 2
y = -3
y = -5x + 2 Substitute in 2 for x
y = -5(2) + 2
y = -10 + 2
y = -8
Helping in the name of Jesus.
What is the value of the underlined digit?
5(3)
Enter the correct answer in the box.
Answers
Answer: tens
Step-by-step explanation:
PLS ANSWER GIVING 15 POINTS!!!

Answers
Answer:
Instead of adding the exponents of 2 to get four you should just leave the exponent as two in the final answer.
A bottle of water has a diameter of 3 inches and a height of 8 inches, and a mass of 1250 g. What is the volume and density?
Answers
The volume of the bottle is 56.52 cubic inches, and the density is 22.12 g/in³.
What is the volume and density of the bootle water?The volume of a cylinder is expressed as;
V = π × r² × h
Where r is radius of the circular base, h is height and π is constant pi ( π = 3.14 ).
Density is expressed mathematically as;
p = m / v
Where m is mass and v is volume.
Given that:
Diameter = 3 in
Radius r = diameter/2 = 3/2 = 1.5 in
Height h = 8 in
Mass m = 1250 g
Find the volume:
V = π × r² × h
V = 3.14 × (1.5 in )² × 8in
V = 56.52 in³
Find the density:
p = m / v
p = 1250g / 56.52 in³
p = 22.12 g/in³
Therefore, the density is 22.12 g/in³.
Learn more about density here: brainly.com/question/952755
#SPJ1
52 is what percent of 156?
Answers
Answer:
33.33
Step-by-step explanation:
Answer:
about 33.33
Step-by-step explanation:
Help please friendssssssssss

Answers
Answer: 6/(6+2x) ; (-infinity, -3) U (-3, infinity)
Step-by-step explanation:
(a) This can be read as f(x) composed of g(x). Plug in the expression given for g(x) for every x value in f(x):
(6/x)/(6/x+2)
I gave the terms in the denominator the same denominator to combine the bottom two terms into one term. 6/x + 2 is equal to 6/x + 2x/x -->
(6 +2x)/x
Do the classic keep, change, flip. \(\frac{6}{x} * \frac{x}{6+2x}\)
This simplifies to: \(\frac{6}{6+2x}\)
(b) Domain is all real numbers except for what makes the denominator equal to 0. 6 + 2x = 0 when x = -3. Therefore it is all real numbers except -3.
What is the length of each segment on the number line
Answers
Answer:
The length of line segment is 3 -(-3) = 6 units
Step-by-step explanation:
Here is the equation help

Answers
Answer: this might help I’m not sure
Step-by-step explanation:

Answer:
5m+3m=8m
simplified
Step-by-step explanation:
combine all m's together 5m's +3m's =8m's
(☆▽☆)
For each graphically defined function below, state the domain, the range, and the intervals over which the function is increasing, decreasing, or constant.

Answers
The domain of the function above is [-2, 3].
The range of the function above is [-2.5, 2].
The intervals over which the function is increasing is [-2, 1.5] U [-2.5, 2].
The intervals over which the function is decreasing is [1.5, -2.5].
What is a domain?In Mathematics and Geometry, a domain refers to the set of all real numbers for which a particular function is defined.
Furthermore, the vertical extent of any graph of a function represents all range values and they are always read and written from smaller to larger numerical values, and from the bottom of the graph to the top.
By critically observing the graph of this rational expression (function) shown in the image attached below, we can reasonably and logically deduce the following domain and range:
Domain = [-2, 3] or -2 ≤ x ≤ 3.
Range = [-2.5, 2] or -2.5 ≤ y ≤ 2.
Additionally, the intervals over which the function is increases over the interval [-2, 1.5] and [-2.5, 2], while it decreases over the interval [1.5, -2.5].
In conclusion, the given function is not constant over any interval.
Read more on domain here: brainly.com/question/17003159
#SPJ1
What is a transformation
Answers
Answer:
A transformation is a general term for four specific ways to manipulate the shape and/or position of a point, a line, or geometric figure.
Find the area of the circle.
Use 3.14 for n. Do not round your answer.
Hint: A = tira
18 inches
=
Area = [?] inches
]
Enter the number that
belongs in the green box.
![Find the area of the circle.Use 3.14 for n. Do not round your answer.Hint: A = tira18 inches=Area = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/LPTZuJocrx2rSs87WchkQh3Q0SibUyN1.png)
Answers
Answer:
The answer is 254.34 square inches
Step-by-step explanation:
Given;Diameter (d) = 18 inchesπ = 3.14To Find;Area of CircleFormula;A = π r²Now,
Radius = Diameter ÷ 2
r = 18/2 = 9 inches
So,
A = π r²
A = 3.14 × 9² inches
A = 3.14 × 81 inches
A = 254.34 square inches
Thus, The area of the circle is 254.34 square inches
-TheUnknownScientist 72
Find the area of the rectangle on this centimetre grid.
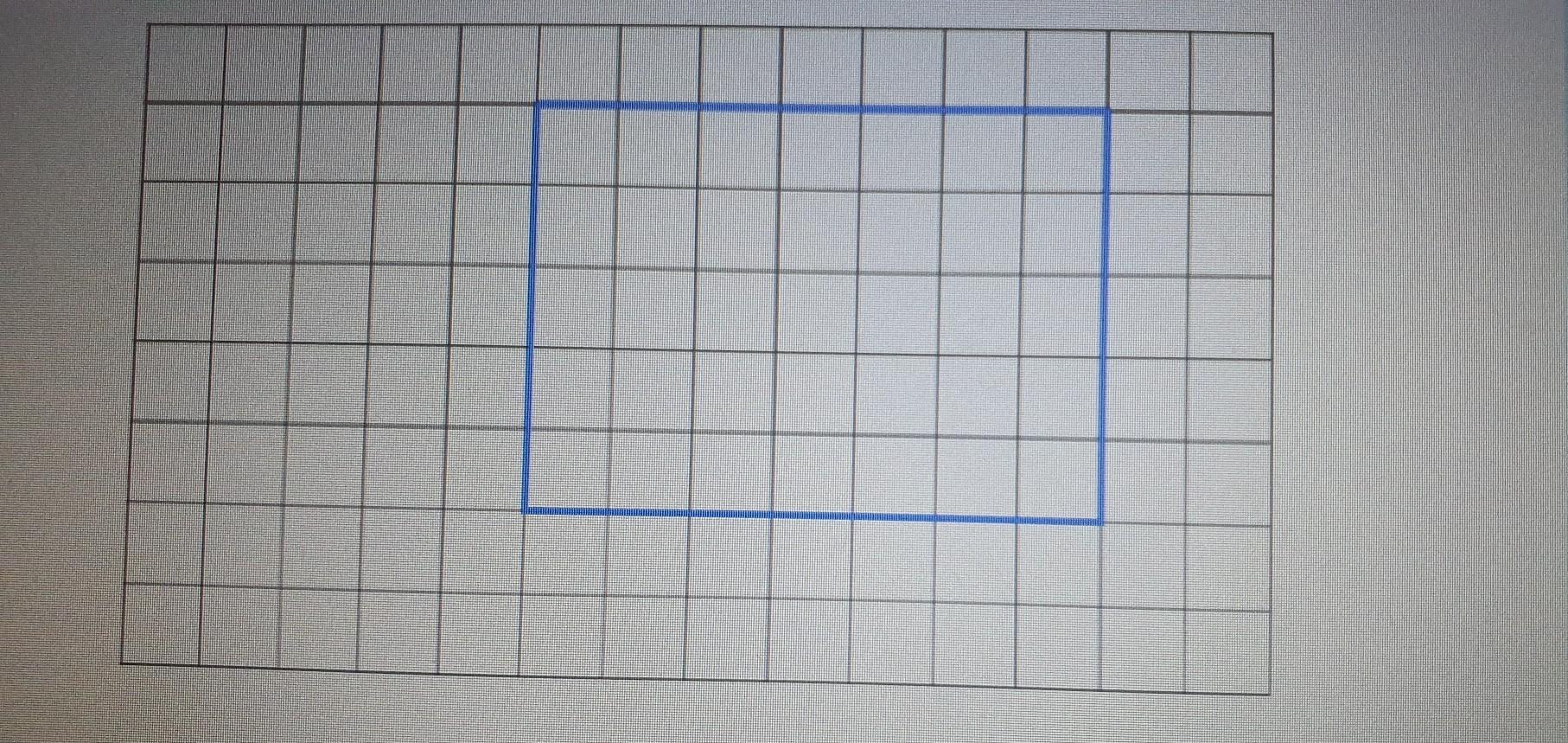
Answers
Answer:
A = 35 cm²
Step-by-step explanation:
the area (A) of a rectangle is calculated as
A = length × width
by counting the squares on the sides
length = 7 cm and width = 5 cm , then
A = 7 × 5 = 35 cm²
Geomtry question pls help !!!
If the length of segment RQ is 8,what is the length of segment PQ?
A-5
B-2
C-4
D-3

Answers
Answer:
C, 4.
Step-by-step explanation:
Im not sure how to explain it, i just know that it's C! :))
Amazon is offering a $1000 hiring bonus and they will pay $16 per hour for 25 hours per week. UPS is offering a $50 weekly bonus for working on Sunday and they will pay $18 per hour for 30 hours per week. Assuming you will earn the bonus from either place, at some point you will make the same total pay at each job. How much is that total pay
Answers
Using the equations, the total pay adding pay at each job is obtained to be $1590.
What is an equation?
A mathematical definition of an equation is a claim that two expressions are equal when they are joined by the equals sign ("=").
Let's start by finding the total pay earned at Amazon in a week -
Hourly wage = $16
Weekly hours worked = 25
The equation will be -
Regular weekly pay = Hourly wage × Weekly hours worked
Regular weekly pay = $16 × 25
Regular weekly pay = $400
Hiring bonus = $1000
The equation will be -
Total pay earned in a week = Regular weekly pay + Hiring bonus
Total pay earned in a week = $400 + $1000
Total pay earned in a week = $1400
Now, let's find the total pay earned at UPS in a week.
Hourly wage = $18
Weekly hours worked = 30
The equation will be -
Regular weekly pay = Hourly wage × Weekly hours worked
Regular weekly pay = $18 × 30
Regular weekly pay = $540
Sunday bonus = $50
The equation will be -
Total pay earned in a week = Regular weekly pay + Sunday bonus
Total pay earned in a week = $540 + $50
Total pay earned in a week = $590
We want to find the point at which the total pay earned at each job is the same, so we can set the two expressions for total pay equal to each other and solve for the unknown variable (the number of weeks worked) -
$1400 = $590n, where n is the number of weeks worked
Solving for n, we get -
n = $1400/$590 ≈ 2.37
So, the total pay earned will be the same for both jobs after working for about 2.37 weeks (or about 17 days).
At that point, the total pay earned at either job will be -
Total pay = Regular weekly pay + Hiring bonus + Sunday bonus
Total pay = $540 + $50 + $1000
Total pay = $1590
Therefore, the total pay value is $1590.
To learn more about equation from the given link
https://brainly.com/question/28871326
#SPJ1
Mark what answer it is

Answers
2/29
the i is imaginary
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
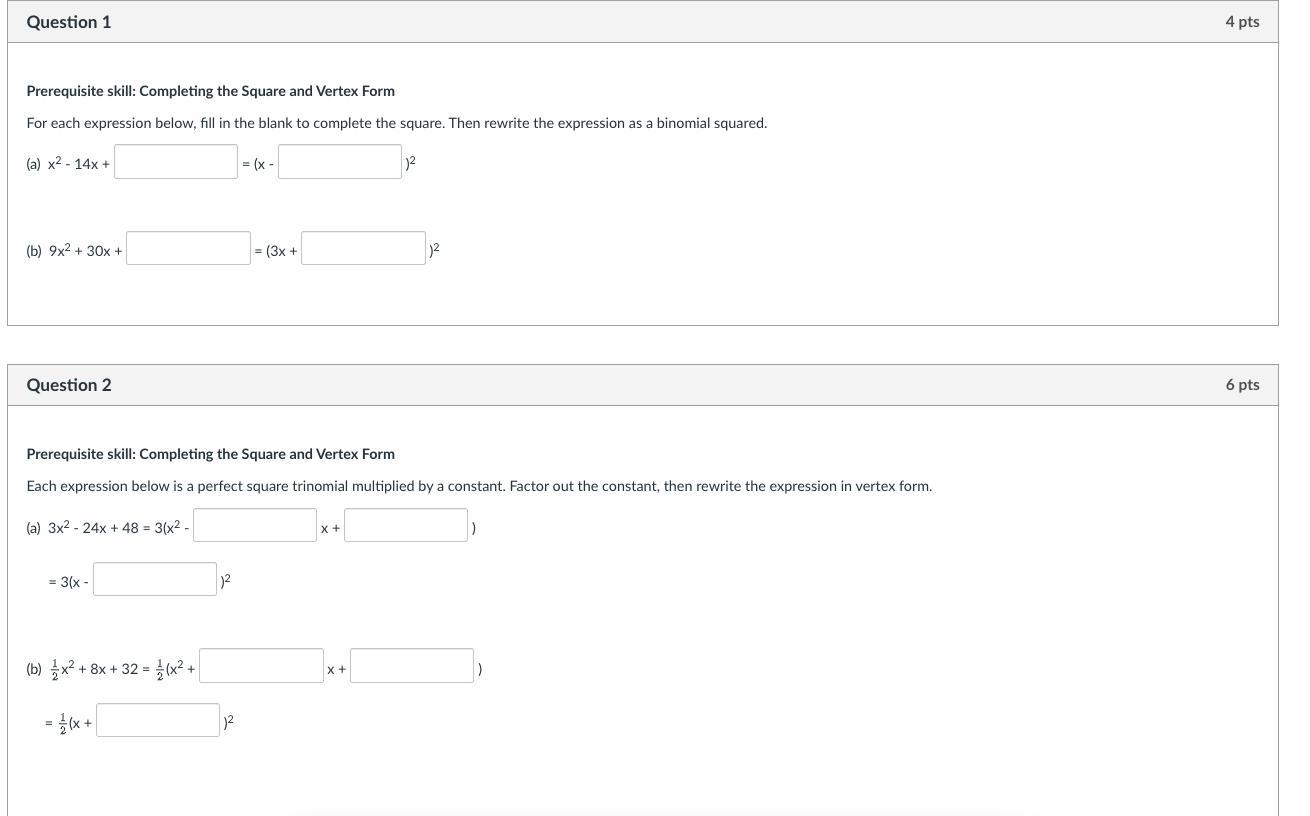
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Simplify the linear expression
-5/8a+2/3-1/4a-5/6
Enter your answer as simplified fractions in the boxes.

Answers
Answer:
\(\huge\boxed{-\frac{7}{8}a - \frac{1}{6}}\)
Step-by-step explanation:
This question utilizes combining like terms and common denominators. First you have to convert both terms including "a" to have a denominator of 8. You would do this by multiplying both the numerator, and the denominator by the same value. This value in the case of \(-\frac{1}{4} a\) would be 2, and in the case of \(\frac{2}{3}\) the value would be 2. This would result in the equation: \(-\frac{5}{8}a+\frac{4}{6}-\frac{2}{8}a-\frac{5}{6}\). Then simply combine like terms to get your final answer.
What’s the answer ?
2003 4/11
+
59
=
Answers
Answer:
2062 4/11
Step-by-step explanation:
Okay so assuming 2003 4/11 is a mixed number, we just add:
2003 4/11 + 59 = 2062 4/11
Hope this helps:)
Use your exponent rules to express as a single power, 9^4 ÷ 27^2
Make sure to do it step by step
Answers
Answer:
9
Step-by-step explanation:
9^4=3^8
27^2=3^6
when we divide the powers of the same base ,we take the common base and subtract their exponent.
3^8-^6
=3^2
=9
The measure of the angle is 17 times greater than its supplement.
Answers
Answer: supplement <17
Step-by-step explanation:
1. 17 is greater
2. supplement is smaller
A quick quiz consists of a multiple-choice question with 5 possible answers followed by a multiple-choice question with 6 possible answers. If both questions are answered with random guesses, find the probability that both responses are correct.
Answers
The probability that the submitted responses to the questions were correct will be 2/11.
What is probability?Simply put, the probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes.
Statistics is the study of events that follow a probability distribution.
Mathematics' study of random events is known as probability, and there are four primary types of probability: axiomatic, classical, empirical, and subjective.
So, the probability formula is as follows:
Probability = Favourable events/Total events
Now, insert values as follows:
Probability = Favourable events/Total events
Probability = 1+1/5+6
Probability = 2/11
Therefore, the probability that the submitted responses to the questions were correct will be 2/11.
Know more about the probability here:
https://brainly.com/question/24756209
#SPJ1
A right triangle has side lengths 9, 40, and 41 as shown below.
B
40
Use these lengths to find cosB, tanB, and sin B.
9
Answers
Answer:
cos B = 9/41
tan B = 40/9
sin B = 40/41
Step-by-step explanation:
There is no picture, so I am making a few assumptions.
I am assuming that angle C is the right angle and is opposite 41.
I am also assuming that angle B is formed by the sides that measure 9 and 41. The hypotenuse is 41.
For angle B, the adjacent leg is 9, and the opposite leg is 40.
cos B = adj/hyp = 9/41
tan B = opp/adj = 40/9
sin B = opp/hyp = 40/41
tan B= 40/9
sin B= 40/41
Isosceles triangle JKL has a perimeter of 16 with the following vertices:
J(5,-2)
K(2,2)
L(x, 2)
What is the x-coordinate for point L?

Answers
The Isosceles triangle JKL has two equal sides
The x-coordinate of point L is 2 or 8
How to determine the x-coordinate of LThe coordinates of the triangle are given as:
J = (5,-2)
K = (2,2)
L = (x, 2)
Start by calculating the distance between the vertices using the following distance formula
\(d = \sqrt{(x_2 -x_1)^2 + (y_2 -y_1)^2}\)
So, we have:
\(JK = \sqrt{(5 -2)^2 + (-2 -2)^2} = 5\)
\(KL = \sqrt{(2 -x)^2 + (2 -2)^2} = 2 -x\)
\(JL = \sqrt{(5 -x)^2 + (-2 -2)^2} = \sqrt{(5 -x)^2 + 16}\)
The triangle is an isosceles triangle.
So, we have:
JK = JL
The equation becomes
\(\sqrt{(5 - x)^2 + 16} = 5\)
Take the square of both sides
\((5 - x)^2 + 16 = 25\)
Subtract 16 from both sides
\((5 - x)^2 = 9\)
Take the square root of both sides
\(5 - x = \pm3\)
Solve for x
\(x = 5 \pm 3\)
x = 2, or 8
Hence, the x-coordinate of point L is 2 or 8
Read more about isosceles triangles at:
https://brainly.com/question/1475130