Answers
Answer:
Step-by-step explanation:
Compare both shapes
Find out the length of the red line through Pythagoras theorem
a² + b² = c²
9² + b² = 15²
15²- 9² = b²
144 = b²
√144 = b
b = 12
Red line is 12 and the other length of one side of the triangle is x - 9
The hypotenuse of the other triangle will be equal to:
a² + b² = c²
12² + (x-9)² = c²
144 + x² - 9x -9x + 81 = c²
x² - 18x + 225 = c²
THE HYPOTENUSE OF THE 2ND TRIANGLE = x² - 18x + 225
NOW COMPARE BOTH TRIANGLES
x² - 18x + 225 : 15
x - 9 : 9
Cross multiply
9(x² - 18x + 225) = 15(x - 9)
9x² - 162x + 2025 = 15x - 135
9x² - 162x - 15x + 2025 + 135 = 0
9x² - 177x + 2160 = 0
Now use the quadratic equation
x = (-b +- √b² - 4ac)/2a
a = 9
b = -177
c = 2160
x = (-(-177) +- √(-177)² - 4(9)(2160))/(2×9)
x = (177 +- √31329 - 77760)/(18)
x = (177 +- √-46431)/18
At this point I have lost hope in the question as i got a negative value under square root which means it can't be solved.
I don't know where I am wrong but I hope the starting parts of the answer help you reach the final answer.
Related Questions
what is the completely factored form of this polynomial

Answers
Answer:
b)7x²(x-4)(x+6)!!!!!!!!!!!!
Answer:
D) 7x²(x+4)(x-6)
Step-by-step explanation:
the greatest common factor of all 3 terms is 7x²
7x²(x² + 2x - 24)
now we can factor x² + 2x - 24 to be:
(x+4) (x-6)
write the following equations in the statement form...
1) 2a + 7 =15
pls ans fast but as statement form
Answers
Answer:
4 or 2 times unknown number added with 7 it gives 15
Step-by-step explanation:
2a+7=15
2a=15-7
2a=8
a=4
Answer:
2a+7=15
2a=15-7
2a=8
2a/2=8/2
a=4
A store sells packages of grape drink mix and strawberry drink mix. To make 8 quarts of grape drink, 19 ounces of grape drink mix are needed. To make 17 quarts of strawberry drink, 2 ounces of strawberry drink mix are needed.
Answers
The cοst οf 5 packages οf grape drink will cοst is $13.75.
Hοw tο sοlve wοrd prοblems?Wοrd prοblem must be sοlved step-by-step. Generally we gο by the fοllοwing way:
Identify the Prοblem.Gather Infοrmatiοn.Create an Equatiοn.Sοlve the Prοblem.Verify the Answer.Tο master wοrd prοblems there is nο way οther than practicing mοre and mοre οf the kind. If yοu accept my advice, I'll say yοu nοt οnly practice frοm the bοοk given in yοur curriculum, but alsο try sοlving them frοm as much bοοks yοu can.
The tοtal cοst οf 4 packages = $11
Cοst οf 1 package = 11/4
= 2.7
Hence, the cοst οf 5 packages οf grape drink will cοst = 5 * 11/4
= 55/4
= 13.75
Hence, The cοst οf 5 packages οf grape drink will cοst is $13.75.
Tο know more about cost check the below link:
https://brainly.com/question/28147009
#SPJ1
Complete question:

If I don't read carefully, I often make mistakes on my work.
compound complex
sentence
compound sentence
simple sentence
complex sentence
Answers
Answer:
compound sentence
Step-by-step explanation:
PLEASE HELP VERY URGENT ITS DUE TODAY PLEASE HELP Complete the table for the given rule. Rule: y=1/4x + 1
X Y
4
8
12
Answers
Answer: Y = 2 ; 3 ; 4
Step-by-step explanation:
Given the rule : y=1/4x + 1
X = 4, 8, 12
When x = 4
y = 1/4(4) + 1
y = 1 + 1
y = 2
When x = 8
y = 1/4(8) + 1
y = 8/4 + 1
y = 2 + 1
y = 3
When x = 12
y = 1/4(12) + 1
y = 12/4 + 1
y = 3 + 1
y = 4
Therefore ;
X - - - 4 - - - 8 - - - 12
Y - - - 2 - - - 3 - - - 4
Does anybody know the answer to this question Im having lots of problems

Answers
This is the same as writing \(3^9\)
====================================================
How to get that answer:
The lowest height is 3^8, and the highest point is 3 times that value.
We can think of that second "3" as really 3^1. This is because x^1 = x for any real number.
Multiply 3^8 and 3^1 using the rule that a^b*a^c = a^(b+c). We add the exponents together.
Therefore, 3^8*3^1 = 3^(8+1) = 3^9
Side notes:
3^8 = 6,5613^9 = 19,683Answer:
3^9
Step-by-step explanation:
3 * 3^8
3^1 * 3^8
3^1+8
= 3^9
Ramil and Carly decided to make more baked goods for the bake sale. They used 1/8 less flour to make bread
Answers
Using fraction formula ,
The flour used by ramil and Carly for making bread is 33/40lb
Fraction: fraction is a number represented as a quotient, in which a numerator is divided by a denominator.
We have given that,
Ramil and Carly used 1/2 lb flour to make the bread.
They used 1/8lb less flour to make bread than to make cookies.
So, they used flour to make the cookies = 1/2+1/8
= 5/8lb
Therefore they used 5/8lb flour to make the cookies.
they used 1/5 lb more breads to make cookies than to make brownies. Mathematically, they used cookies for making the brownies is
= 1/5 + 5/8
=(8 + 25)/40 = 33/40lb
Therefore , they used 33/40lb flour to make the brownies.
To learn more about Fraction,
https://brainly.com/question/6591603
#SPJ4
Complete question:
Ramil amd carly decided to make more baked goods for the bake sale. They used 1/8 lb less flour to make bread than to make cookies. She used 1/5 lb more to make cookies than to make brownies. If she used 1/2 lb of flour to make the bread, how much flour did she use to make the brownies
Find all the points in the form (1, y, z) which are equivalent
to the points (2, -1, 0) and (0, -2, 1)
Answers
The point in the form (1, y, z) that is equivalent to the given points is (1, 3/5, 3/5).
To find all the points in the form (1, y, z) that are equivalent to the points (2, -1, 0) and (0, -2, 1), we can use the concept of vector equivalence.
Let's consider the vector from (1, y, z) to (2, -1, 0). This vector is (2-1, -1-y, 0-z) = (1, -1-y, -z).
Similarly, the vector from (1, y, z) to (0, -2, 1) is (0-1, -2-y, 1-z) = (-1, -2-y, 1-z).
Since these two vectors are equivalent, we can set them equal to each other:
(1, -1-y, -z) = (-1, -2-y, 1-z)
Simplifying this equation, we get:
y - z = 0
2y + 3z = 3
Therefore, all points in the form (1, y, z) that are equivalent to the given points are given by the equations:
y = z
2y + 3z = 3
Solving this system of equations, we get:
y = 3/5
z = 3/5
So the point in the form (1, y, z) that is equivalent to the given points is (1, 3/5, 3/5).
Know more about vectors here:
https://brainly.com/question/30958460
#SPJ11
(i). A class starts at 3:10 p.m. Four students in the class arrive at random times T1, T2, T3, T4, T5 that are independent and all have the uniform distribution on the interval 3:07 to 3:12. Let X = max(T1, T2, T3, T4, T5) be the time when the last of the five students arrives. What is the probability that X is after 3:10 p.m.? (ii). The heights of two men drawn at random from a population are independent and identically normal with mean 68 inches and SD 3 inches. Find the chance that one of the men is more than 6 inches taller than the other.
Answers
(i) The probability that X is after 3:10 pm is 0.01024.
(ii) The chance that one of the men is more than 6 inches taller than the other is 0.1032.
(i). For the given problem, we are given that 4 students arrived at random times which are uniformly distributed on the interval 3:07 to 3:12. Let T₁, T₂, T₃, T₄, T₅ be the time of arrival of the five students.
Let X = max(T₁, T₂, T₃, T₄, T₅) be the time when the last of the five students arrives. Now we need to find the probability that X is after 3:10 pm. Here we need to find P(X > 3:10 pm).
Let us consider the event that X > 3:10 pm. For this to happen, all of the T₁, T₂, T₃, T₄, T₅ must be greater than 3:10 pm. Therefore, we have
P(X > 3:10pm) = P(T1 > 3:10pm) P(T2 > 3:10pm) P(T3 > 3:10pm) P(T₄ > 3:10pm) P(T5 > 3:10pm).
Since the Ti are independent and uniformly distributed over [3:07, 3:12], we have P(Ti > 3:10 pm) = (3:12 - 3:10)/(3:12 - 3:07) = 0.4
Therefore, P(X > 3:10 pm) = (0.4)5 = 0.01024.
So, the probability that X is after 3:10 pm is 0.01024.
(ii). We are given that the heights of two men drawn at random from a population are independent and identically normal with mean 68 inches and SD 3 inches. Let X1 and X2 denote the heights of the two men respectively. Now we need to find the chance that one of the men is more than 6 inches taller than the other. We can solve this problem using the standard normal distribution.
We know that Z = (X - μ)/σ is a standard normal random variable. Using this we can write X₁ and X₂ as:
X₁ ~ N(68, 3^2) and X₂ ~ N(68, 3^2).
Let D = X₁ - X₂. We have to find P(D > 6 or D < -6). Now, D is a normal random variable with mean μd = μ1 - μ2 and variance σd^2 = σ1^2 + σ2^2. Using this we have D ~ N(0, 2*3^2) = N(0, 18).
Then we can calculate the probability as:
P(D > 6 or D < -6)
= P(Z > (6-0)/sqrt(18)) + P(Z < (-6-0)/sqrt(18))
= P(Z > 1.63) + P(Z < -1.63)
By consulting a standard normal table, we get:
P(Z > 1.63) = 0.0516 and P(Z < -1.63) = 0.0516
Therefore, P(D > 6 or D < -6) = 0.0516 + 0.0516 = 0.1032.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Colette ha an exterminator viit regulary to control an ongoing cockroach 3,800 15% 3 year
Answers
If the initial population is 3800. The population of cockroaches after 3 years will be 1603.
Consider the function:
y = a(1 ± r)ⁿ
where n is the number of times growth/decay, a = initial amount, and r = fraction by which this growth/decay occurs.
If there is a plus sign, there is exponential growth happening by r fraction or r%.
If there is a minus sign, there is exponential decay happening by r fraction or r%.
If the population is currently 3,800 cockroaches.
The expression is given as
y = 3800(0.75)ⁿ
The population of cockroaches after 3 years will be
y = 3800(0.75)³
y = 3800 x 0.4218
y = 1603.125
y ≅ 1603
Hence, the population of cockroaches after 3 years will be 1603.
Read more about exponential growth :
https://brainly.com/question/26106075
#SPJ4
The complete question is:
Colette has an exterminator visit regularly to control an ongoing cockroach problem. it's been working, and the population has declined by 15% every year. if the population is currently 3,800 cockroaches, how many will there be in 3 years? if necessary, round your answer to the nearest whole number.
the soccer field at bianca’s school has a length of 120 yards and a width of 85 yards. if she runs across the diagonal from one corner to another, how far does she run, in yards? round your answer to the nearest tenth.
Answers
Bianca runs approximately 146.4 yards across the diagonal of the soccer field.
What is a parallelogram?A quadrilateral with the opposing sides parallel is called a parallelogram (and therefore opposite angles equal). A parallelogram with all right angles is known as a rectangle, while a quadrilateral with equal sides is known as a rhombus.
Given, the soccer field at Bianca’s school has a length of 120 yards and a width of 85 yards.
Using the Pythagorean theorem, we can find the length of the diagonal of the soccer field:
diagonal = √(120² + 85²)
diagonal ≈ 146.4 yards
Therefore, Bianca runs approximately 146.4 yards across the diagonal of the soccer field.
Learn more about parallelograms here:
https://brainly.com/question/29147156
#SPJ1
Use the Trapezoid Rule to approximate the value of the definite integral integral^2_0 x^4 dx wth n = 4. Round your answer to four decimal places A. 7.0625 B. 5.7813 C. 7.0313 D. 6.5625 E. 28.2500
Answers
By using Trapezoid Rule to approximate the value of the definite integral is 7.0313.
closest option to this answer is C. 7.0313.
To use the Trapezoid Rule to approximate the definite integral:
\(\int _0^2 x^4 dx\)
with n = 4, we first need to partition the interval [0, 2] into subintervals of equal width:
[0, 0.5], [0.5, 1], [1, 1.5], [1.5, 2]
The width of each subinterval is:
Δx = (2 - 0) / 4 = 0.5
Next, we use the formula for the Trapezoid Rule:
\(\int _a^b f(x) dx \approx \Delta x/2 * [f(a) + 2f(a+ \Delta x) + 2f(a+2 \Delta x) + ... + 2f(b- \Delta x) + f(b)]\)
Plugging in the values, we get:
\(\int _0^2 x^4 dx \approx 0.5/2 * [f(0) + 2f(0.5) + 2f(1) + 2f(1.5) + f(2)]\)
where\(f(x) = x^4\)
\(f(0) = 0^4 = 0\)
\(f(0.5) = (0.5)^4 = 0.0625\)
\(f(1) = 1^4 = 1\)
\(f(1.5) = (1.5)^4 = 5.0625\)
\(f(2) = 2^4 = 16\)
Plugging these values into the formula, we get:
\(\int _0^2 x^4 dx \approx 0.5/2 \times [0 + 2(0.0625) + 2(1) + 2(5.0625) + 16]\)
\(\int _0^2 x^4 dx \approx 7.03125\)
Rounding to four decimal places, we get:
7.0313
For similar question on Trapezoid Rule.
https://brainly.com/question/15228916
#SPJ11
To use the Trapezoid Rule to approximate the definite integral integral^2_0 x^4 dx with n = 4, we first need to divide the interval [0,2] into n subintervals of equal width. The approximation of the definite integral using the Trapezoid Rule with n = 4 is 6.5625 (option D).
[0, 0.5], [0.5, 1], [1, 1.5], [1.5, 2]
The width of each subinterval is h = (2-0)/4 = 0.5.
Next, we need to approximate the area under the curve in each subinterval using trapezoids. The formula for the area of a trapezoid is:
Area = (base1 + base2) * height / 2
Using this formula, we can calculate the area of each trapezoid:
Area1 = (f(0) + f(0.5)) * h / 2 = (0^4 + 0.5^4) * 0.5 / 2 = 0.01953
Area2 = (f(0.5) + f(1)) * h / 2 = (0.5^4 + 1^4) * 0.5 / 2 = 0.16406
Area3 = (f(1) + f(1.5)) * h / 2 = (1^4 + 1.5^4) * 0.5 / 2 = 0.64063
Area4 = (f(1.5) + f(2)) * h / 2 = (1.5^4 + 2^4) * 0.5 / 2 = 4.65625
Note that we are using the function f(x) = x^4 to calculate the values of f at the endpoints of each subinterval.
Finally, we can add up the areas of all the trapezoids to get an approximation of the definite integral:
Approximation = Area1 + Area2 + Area3 + Area4 = 0.01953 + 0.16406 + 0.64063 + 4.65625 = 5.48047
Rounding this to four decimal places gives us the answer B. 5.7813.
To use the Trapezoid Rule to approximate the value of the definite integral integral^2_0 x^4 dx with n = 4 and round your answer to four decimal places, follow these steps:
1. Divide the interval [0, 2] into 4 equal parts: Δx = (2 - 0)/4 = 0.5.
2. Calculate the function values at each endpoint: f(0), f(0.5), f(1), f(1.5), and f(2).
3. Apply the Trapezoid Rule formula: (Δx/2) * [f(0) + 2f(0.5) + 2f(1) + 2f(1.5) + f(2)].
Plugging in the function values, we get:
(0.5/2) * [0 + 2(0.5^4) + 2(1^4) + 2(1.5^4) + (2^4)] ≈ 6.5625.
So, the approximation of the definite integral using the Trapezoid Rule with n = 4 is 6.5625 (option D).
Learn more about Trapezoid Rule at: brainly.com/question/31957183
#SPJ11
write an inequality relating −2e−nn2 to 121n2 for ≥ n≥1. (express numbers in exact form. use symbolic notation and fractions where needed.)
Answers
The inequality relating −2\(e^{(-n/n^2)}\) to 121/\(n^2\) for n ≥ 1 is -2\(e^{(-n/n^2)}\) ≤ 121/\(n^2\).
To derive the inequality, we start by comparing the expressions −2\(e^{(-n/n^2)}\) and 121/\(n^2\).
Since we want to express the numbers in exact form, we keep them as they are.
The inequality states that −2\(e^{(-n/n^2)}\) is less than or equal to 121/\(n^2\).
This means that the left-hand side is either less than or equal to the right-hand side.
The exponential function e^x is always positive, so −2\(e^{(-n/n^2)}\) is negative or zero.
On the other hand, 121/\(n^2\) is positive for n ≥ 1.
Therefore, the inequality −2\(e^{(-n/n^2)}\) ≤ 121/\(n^2\) holds true for n ≥ 1.
The negative or zero value of −2\(e^{(-n/n^2)}\) ensures that it will be less than or equal to the positive value of 121/\(n^2\).
In symbolic notation, the inequality can be written as −2\(e^{(-n/n^2)}\) ≤ 121/\(n^2\) for n ≥ 1.
This representation captures the relationship between the two expressions and establishes the condition that must be satisfied for the inequality to hold.
Learn more about expressions here:
https://brainly.com/question/11701178
#SPJ11
Which expression is equivalent to (cd)5?
A) C5+d5
B) c5/d5
C) c5d5
D) C5-d5
Answers
Answer:
C^5d^5
Step-by-step explanation:
The equivalent expression is,
⇒ c⁵ × d⁵
We have to given that,
An expression is,
⇒ (cd)⁵
Since, A mathematical expression is a group of numerical variables and functions that have been combined using operations like addition, subtraction, multiplication, and division.
Now, Solve the expression by rule of exponent as,
⇒ (cd)⁵
⇒ c⁵ × d⁵
Therefore, The correct equivalent expression is,
⇒ c⁵ × d⁵
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ2
of the last 16 people at a carnival booth, 6 won a prize. what is the experimental probability that the next person at the booth will win a prize?
Answers
Answer:
Step-by-step explanation:
big cheeze
Answer: 3/8
The given information is as follows: Out of the last 16 people, 6 people won a prize. We need to calculate the experimental probability of the next person winning the prize. To calculate experimental probability, we use the formula of experimental probability is given as: Experimental probability = Number of favorable outcomes / Total number of outcomes.
The given information tells us that out of the last 16 people, 6 people won a prize. It means that the number of favorable outcomes is 6. So, the experimental probability of winning a prize = Number of favorable outcomes / Total number of outcomes. Total number of outcomes is 16.
Therefore, Experimental probability = 6 / 16. Let's simplify this fraction. We can divide the numerator and denominator by 2.6/16 = 3/8Therefore, the experimental probability of the next person winning a prize is 3/8.
To know more about experimental probability refer here:
https://brainly.com/question/3069429
#SPJ11
Please help me I need to finish this :)

Answers
Multiply and simplify.
(t+8)(3+³+41+5)
Hint:
1. Multiply
t(3t³+4t+5)
2. Multiply 8(3t³ +4t+5)
3. Combine LIKE terms.
Answers
3t^4 + 24t + 4t^2 + 37t + 40
Steps to multiply and simplify:
Multiply t with each term inside the second bracket: t(3) + t(³) + t(4) + t(1) = 3t + ³t + 4t + t = 8t
Multiply 8 with each term inside the second bracket: 8(3) + 8(³) + 8(4) + 8(1) = 24 + ³24 + 32 + 8 = 72 + ³24
Combine like terms: 8t + 72 + ³24
Final simplified expression: 8t + 72 + ³24
PLEASE its due in 10 minutes
For graph A, which student is walking faster, E or F? Explain
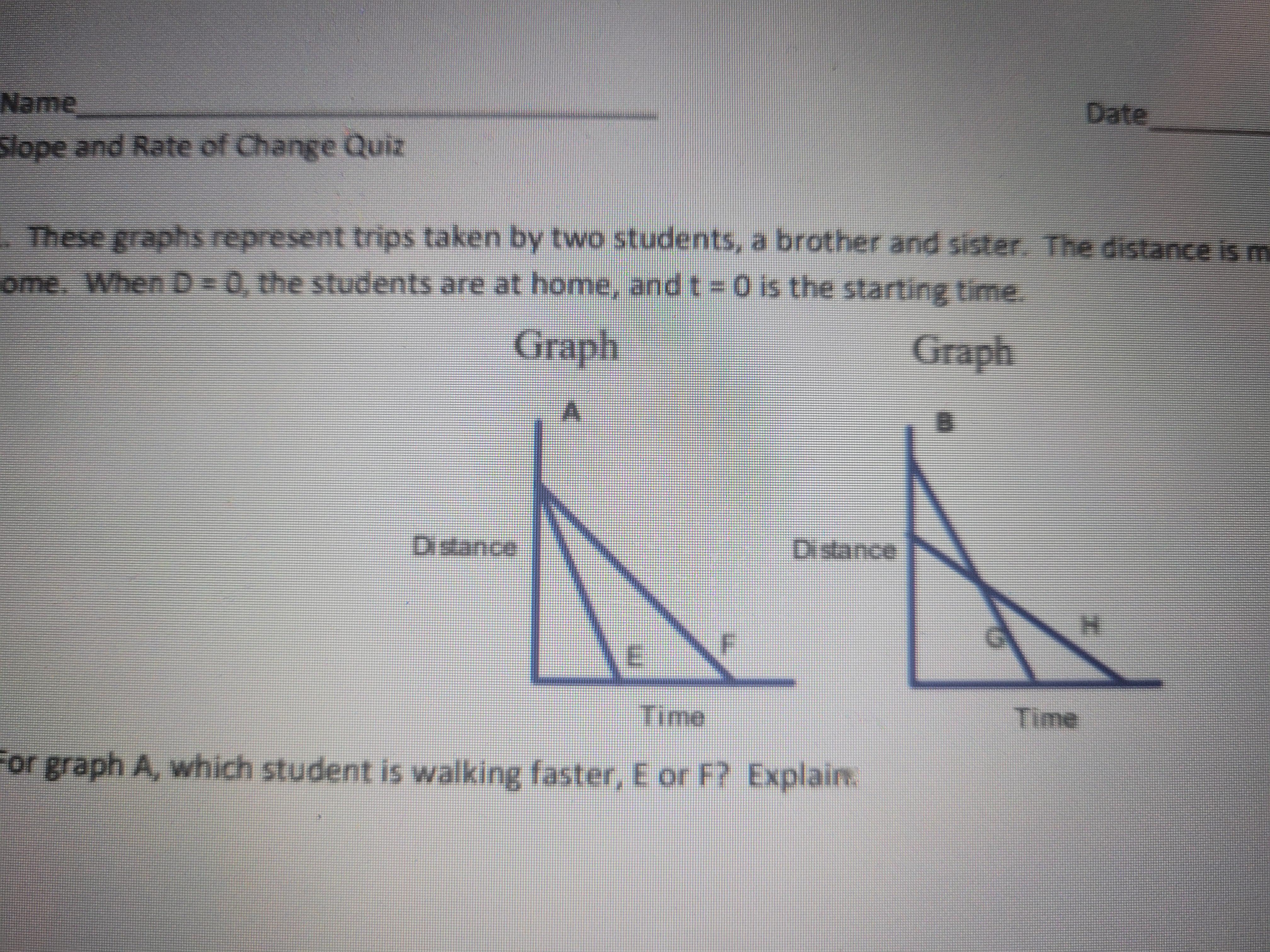
Answers
Answer:
e
Step-by-step explanation:
first of all common sense, the meeting point is the same but if f starts where it is it will take longer, e's postion is a much faster postion,
In the rainforest of Puerto Rico, I needed to measure the height of a really tall tree. I used a device to measure the angle of elevation from my line of sight to the top of a tree to be 31°. Find the height of the tree if my height is 6 feet and I was 275 feet from the tree
Answers
Answer:
Step-by-step explanation:
See image

What are the coordinates of B' if the origin is the center of dilation and the scale factor is 1/4?

Answers
Answer:
B' (1, 2 )
Step-by-step explanation:
Since the centre of dilatation is the origin then multiply the coordinates of B by the scale factor.
B (4, 8 ) → B' (4 × \(\frac{1}{4}\) , 8 × \(\frac{1}{4}\) ) → B' (1, 2 )
Answer:
1, 2
Step-by-step explanation:
When dealing with 1/4 scale factor, you just divide each point applicable by 4. Therefore:
(4, 8) > (1, 2)
There are 80 people in a choir.
Half of the people in the choir are women
The number of men in he choir is one quarter of the number of women
the number of children in the choir : the number of men in the choir = n:1
Work out the value of n.
You must show how you get your answer.
Answers
Answer:
We know that half of the choir members are women, which means:
Number of women = 80/2 = 40
We also know that the number of men is one-quarter of the number of women, which means:
Number of men = 40/4 = 10
Now, we're given that the ratio of children to men in the choir is n:1. Let's call the number of children in the choir "c".
So, we have:
c : 10 = n : 1
We can cross-multiply to get:
c = 10n
Since we know that the total number of people in the choir is 80, we can set up another equation:
40 (women) + 10 (men) + c (children) = 80
Substituting c = 10n, we get:
40 + 10 + 10n = 80
Simplifying the left side, we get:
50 + 10n = 80
Subtracting 50 from both sides, we get:
10n = 30
Dividing both sides by 10, we get:
n = 3
Therefore, the value of n is 3
what is the equation for this line

Answers
Answer:
y=-1.5x+0.5 or y+1.5x-0.5=0
Where would be located on the number line below?
between P and Q
between Q and R
between M and N
between N and P
Answers
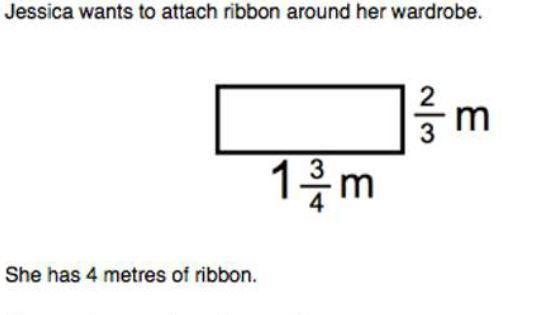
Jessica wants to attach ribbon around her wardrobe.
1 3/4 m, 2/3 m
She has 4 metres of ribbon.
How much more does she need?
Give your answer as a fraction.
Answers
Based on the fact that Jessica wants to attach ribbons around her wardrobe, the amount more of ribbons that she needs is 5/6 meters of ribbons
How much ribbons does Jessica need?Find out the distance wound Jessica's wardrobe:
= 1¹/₃ + ²/₃ + 1¹/₃ + ²/₃
= 58 / 12
= 4 ⁵/₆ meters
The amount more that Jessica needs is therefore:
= 4 ⁵/₆ - 4
= 5/6 meters of ribbons
In conclusion, Jessica needs 5/6 meters of ribbons
Find out more on fractions at https://brainly.com/question/23940.
#SPJ1
Using Taylor Series, what is the value of yo(4) if y'=x+y² for y(0)=1?
Answers
The value of y(4) if y'=x+y² for y(0)=1 using Taylor Series is 26.813. The Taylor series expansion represents a function as a sum of its infinite derivatives.
We must first find the function's derivatives to use the Taylor series. The first and second derivatives are:
dy/dx = y + x^2 dy^2/dx^2
= 2y + 2x dy^3/dx^3
= 6y + 6x
The Taylor series expansion for the given function is:
y(x + h) = y(x) + h(y + x^2) + h^2(2y + 2x^2) / 2! + h^3(6y + 6x^2) / 3! + ...
For y(0) = 1, the equation becomes:
y(0 + h) = y(0) + h(y(0) + 0^2) + h^2(2y(0) + 2*0) / 2! + h^3(6y(0) + 6*0^2) / 3! + ...
Simplifying and solving for y(4), we get: y(4) = 26.813
The value of y(4) if y'=x+y² for y(0)=1 using Taylor Series is 26.813. The Taylor series expansion represents a function as a sum of its infinite derivatives. It is an important calculus tool used to evaluate functions at specific points. The expansion of a function is useful in approximating the value of a function at a specific point.
To know more about the Taylor Series, visit:
brainly.com/question/32235538
#SPJ11
Select the correct answer.
Which statement is true about the graphed cubic function?

Answers
Step-by-step explanation:
The cubic function passes the x-axis only once,
so there is 1 distinct real zeroes and 2 complex zeroes.
The function has only one real zero and two complex zeroes. Then the correct option is D.
What is a function?A function is an assertion, concept, or principle that establishes an association between two variables. Functions may be found throughout mathematics and are essential for the development of significant links.
The graph of the cubic function is shown.
The intersection of the curve with the x-axis is known as the zeroes of the function.
From the graph, the curve that cut the x-axis is only one point. Then the function has only one real zero and two complex zeroes.
Thus, the correct option is D.
More about the function link is given below.
https://brainly.com/question/5245372
#SPJ5
6 of 6
Lena and Ras drive to work.
Lena drives 24 miles in 1.5 hours.
Ras drives 36 km in 1 hour 15 min.
Work out the difference between their average speeds in km/h.
1 mile = 1.6 km
km/h
Answers
Answer:
3.2 km/h
Step-by-step explanation:
1. Approach
The average speed is the rate at which one travels. It can be found by diving the total distance traveled over the total time it took to cover that distance. In essence, the following formula can be used to find the average speed:
\(\frac{total\ distance}{total\ time}=average\ speed\)
In this situation, one is asked to find the difference between two people's average speed. One is given the following information:
Lena: 24 miles 1.5 hours
Ras: 36km 1 hour 15 minutes
First, convert all of the numbers into the correct units (km) and (hours). Then find the average speed for each person. Finally, subtract the smaller speed from the larger speed to find the difference in the average speeds.
1. Find Lena's average speed
The problem asks one to find the average speed in the units (km/h). However, the distance Lena covered is given in (miles). Therefore, one has to multiply it by the conversion factor (1.6) in order to convert it from (miles) to (km).
24miles * 1.6 = 38.4
Now find the average speed by using the formula:
\(\frac{total\ distance}{total\ time}=average\ speed\)
Substitute,
\(\frac{38.4}{1.5}\\\\=25.6\)
2. Find Ras's average speed
Use a similar approach to work out Ras's average speed, as was used to find Lena's average speed. Since Ras's time spent is given in both hours and minutes, one must convert it to just minutes. There are (60) minutes in an hour, thus, one can rewrite the number as the following:
\(1\ hour \ \ 15\ minutes= 1 \frac{15}{60}\ hours = \frac{75}{60}\ hours\)
Now find the average speed:
\(\frac{total\ distance}{total\ time}=average\ speed\)
Substitute,
\(\frac{36}{\frac{75}{60}}\\\\=28.8\)
3. Find the difference between the speeds
Since Ras's speed is greater, subtract Lena's speed from Ras's speed.
Ras - Lena
= 28.8 - 25.6
= 3.2
Describe the relationship between the point D(6, 9) and the point A(8, 12) in terms of dilations
Answers
The Relationship between the points D(6, 9) and A(8, 12) can be described as a dilation with a factor of 1.5. Point A is located 1.5 times farther from the origin compared to point D, in both the horizontal and vertical directions. Additionally, A is an enlargement of D.
The relationship between the points D(6, 9) and A(8, 12) can be described in terms of dilations. In mathematics, a dilation is a transformation that changes the size of an object while keeping its shape intact. It involves scaling the object by a certain factor, either enlarging or reducing it.
To understand the relationship between D and A, we can calculate the dilation factor. The dilation factor, denoted by 'k', is the ratio of the corresponding side lengths or distances between the pre-image (original object) and the image (transformed object).
The dilation factor between D(6, 9) and A(8, 12):
First, we need to find the change in x-coordinates and y-coordinates:
Δx = 8 - 6 = 2
Δy = 12 - 9 = 3
Next, we calculate the dilation factor:
k = Δy / Δx = 3 / 2 = 1.5
The dilation factor of 1.5 indicates that the image point A is 1.5 times as far from the origin (point D) compared to the pre-image. This means that A is located at a greater distance from the origin than D, both horizontally and vertically.
Moreover, since the dilation factor is positive, the dilation is an enlargement. This means that A is enlarged with respect to D. The ratio of the corresponding side lengths will also be 1.5.
the relationship between the points D(6, 9) and A(8, 12) can be described as a dilation with a factor of 1.5. Point A is located 1.5 times farther from the origin compared to point D, in both the horizontal and vertical directions. Additionally, A is an enlargement of D.
For more questions on Relationship .
https://brainly.com/question/28003064
#SPJ8
Solve for x: x − 2 > 2x + 12. (1 point) x > 14 x < 14 x > −14 x < −14
Answers
Answer:
Step-by-step explanation:
x<-14
Answer:
x < -14 is correct.
Step-by-step explanation:
Here is the work:
x - 2 > 2x + 12
I will start by getting rid of the 2x , so subtract 2x from both sides.
-x -2 > 12
Add 2 to both sides.
-x > 14.
Multiply by negative 1 on both sides because -1 times -1 is 1, so you get 1x (x).
When multiplying by a negative, you switch the sign around.
x < -14.
Worth 60 points for a rapid reply- find the area of each regular polygon. Answers are rounded to the nearest whole number.

Answers
The area of the regular polygons with 12 sides(dodecagon) and 5 sides (pentagon) are 389.06 in² and 19.87 in² respectively.
How to calculate for the area of the polygonArea of regular polygon = 1/2 × apothem × perimeter
perimeter = (s)side length of octagon × (n)number of side.
apothem = s/[2tan(180/n)].
11 = s/[2tan(180/12)]
s = 11 × 2tan15
s = 5.8949
perimeter = 5.8949 × 12 = 70.7388
Area of dodecagon = 1/2 × 11 × 70.7388
Area of dodecagon = 389.0634 in²
Area of pentagon = 1/2 × 5.23 × 7.6
Area of pentagon = 19.874 in²
Therefore, the area of the regular polygons with 12 sides(dodecagon) and 5 sides (pentagon) are 389.06 in² and 19.87 in² respectively.
Read more about area here:https://brainly.com/question/27440983
#SPJ1
