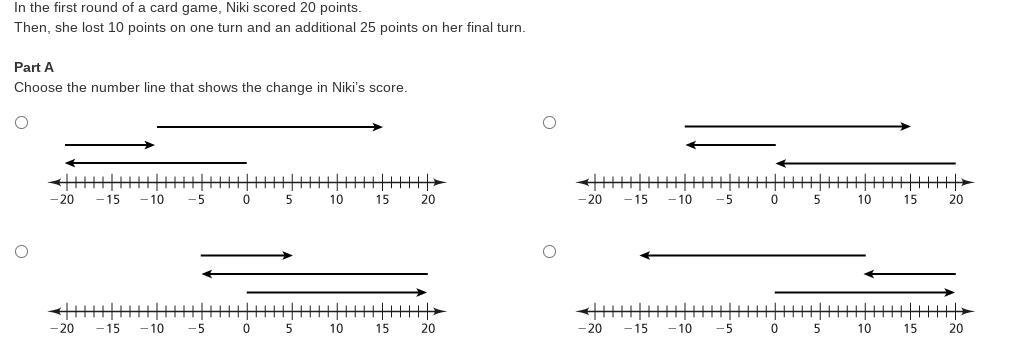
Answers
Answer: D (the bottom right)
Step-by-step explanation: The first problem stated is that Niki scored 20 points (positive) so you would point the arrow directed positively. Then she lost 10 points, which would be negative so the direction of the arrow would point back to a positive 10. Then lost another 25 points, leading to -15 (10+(-25)= -15
Related Questions
A school cafeteria spent $2,700 for ingredients necessary to prepare 450 meals. What is the rate spent per meal?
Answers
Answer:
$6
Step-by-step explanation:
If we divide the amount they spend by the amount of meals they make, we get 6. So this means that they spend $6 per meal.
Find the derivative of the function by the limit process. f(x) = x² + x − 8 f'(x) = Submit Answer 2. [-/2 Points] DETAILS The limit represents f '(c) for a function f(x) and a number c. Find f(x) and c. [7 − 2(3 + Ax)] − 1 - lim ΔΧ - 0 Ax f(x) = C =
Answers
1. The derivative of the function by the limit process is f'(x) = 2x + 1.
How do we find the derivative of a function by limit process?1. For the function f(x) = x² + x − 8, we can find the derivative through the limit process this following way;
the derivative of a function at a point \(x = c, f'(c)\), and is defined by the limit as Δx approaches 0 of ⇒ \(\frac{(f(c + \triangle x) - f(c))}{ \triangle x}\)
For f(x) = x² + x - 8, we have:
\(f(x + \triangle x) = (x + \triangle x)^2 + (x + \triangle x) - 8\)
\(= x^2 + 2x \triangle x + \triangle x^2 + x + \triangle x - 8.\)
Substituting into the definition of the derivative gives us:
\(f'(x) = lim (\triangle x = > 0) [(f(x + \triangle x) - f(x)) / \triangle x]\)
= lim (Δx → 0) {(x² + 2xΔx + Δx² + x + Δx - 8) - (x² + x - 8)} / Δx
= lim (Δx → 0) [2xΔx + Δx² + Δx] / Δx
= lim (Δx →0) [2x + Δx + 1]
= 2x + 1 (after Δx → 0).
Find more exercises on limit process;
https://brainly.com/question/5313449
#SPJ4
George wants to buy a new television that is on sale for 1/4 off the regular price of $599.96. The sales tax is 7%. What is the final price of the television including tax?
Answers
Answer:
641.96
Step-by-step explanation:
In a theater, there are 4,500 lower-level seats and 2,000
upper-level seats. What is the ratio of lower-level seats to total
seats?
Answers
The ratio of lower-level seats to the total seats in the theater is approximately 0.6923. This means that for every 1 seat in the upper level, there are approximately 0.6923 seats in the lower level.
The ratio of lower-level seats to the total seats in the theater can be calculated by dividing the number of lower-level seats by the sum of lower-level seats and upper-level seats. In this case, the theater has 4,500 lower-level seats and 2,000 upper-level seats.
To find the ratio, we add the number of lower-level seats and upper-level seats: 4,500 + 2,000 = 6,500.
Then, we divide the number of lower-level seats (4,500) by the total number of seats (6,500): 4,500 / 6,500 = 0.6923.
Therefore, the ratio of lower-level seats to the total seats in the theater is approximately 0.6923. This means that for every 1 seat in the upper level, there are approximately 0.6923 seats in the lower level.
It's important to note that the ratio is typically expressed in the form of "x:y" or "x/y," where x represents the number of lower-level seats and y represents the total number of seats. In this case, the ratio is approximately 4,500:6,500 or 0.6923:1.
Learn more About ratio from the link
https://brainly.com/question/12024093
#SPJ11
Type the correct answer in the box. Use numerals instead of words. What value of x makes this equation true? -2x + 3 = -15 x =
Answers
Answer:
x=9
Step-by-step explanation:
plug in the number 9
-2(9)= -18
-18+3= -15
Una profesora compra 28 manzanas para compartir con sus estudiantes; al día siguiente revisa la cesta con las frutas y ve que se le han dañado 2/7 del total de manzanas que había comprado. Para reponer las frutas dañadas ella debe comprar
Answers
Answer:
La profesora debe comprar 8 manzanas para reponer la cesta de frutas.
Step-by-step explanation:
La profesora debe reponer la cesta de frutas por la cantidad de manzanas que se encuentran dañadas. La cantidad de manzanas dañadas es igual a las dos séptimas partes del total de manzanas. Es decir:
\(x = \frac{2}{7} \times (28\,manzanas)\)
\(x = \frac{56\,manzanas}{7}\)
\(x = 8\,manzanas\)
La profesora debe comprar 8 manzanas para reponer la cesta de frutas.
Which equation can be used to find A, the area of the parallelogram shown?
A parallelogram with a base six meters, height seven meters, and diagonal side length eleven meters
A = 6 × 7
A = 6 × 11
A = 12 × 6 × 7
A = 12 × 6 × 11
Answers
Answer:
A = 6 x 7
Step-by-step explanation:
To find the area of a parallelogram we use the equation of Area = base x height. In this case since the base is 6 and the height is 7, we plus in these numbers for the variables (b x h) to get the area.
Triangle LMN is dilated by a factor of 1.25 to create triangle PQR what is the length of PQ A 20 cm B 18.75 cm C 17 cm di 12 cm
Answers
Answer:
See explanation
Step-by-step explanation:
Given
\(\triangle LMN \to \triangle PQR\)
\(k = 1.25\)
Required
The length of PQ
\(\triangle LMN \to \triangle PQR\) means that the side lengths of LMN are multiplied by 1.25 to get the side lengths of PQR
And it implies that the following sides are corresponding
\(LM \to PQ\)
\(MN \to QR\)
\(LN \to PR\)
So, we have:
\(PQ = k * LM\)
\(PQ = 1.25* LM\)
The question is incomplete.
Assume LM = 16, then:
\(PQ = 1.25* 16\)
\(PQ = 20\)
Please help!
Theresa's Book Barn sold $10,347 worth of books during September. In October, their sales were $12,115. How much higher were Theresa's book sales during October than in September? Explain how you got your answer.
Answers
Answer:
awnser is 1718
Step-by-step explanation:
Answer:
$12,115 - $10,347 = $1,768. the difference is $1,768 this is how much more in sales they had in October
Helpppp!! I’ll mark brainliest if you put it In fraction form as well!!!

Answers
A car windshield wiper and arm is 26 inches long and rotates at an angle of 108.6°. What is the area of the region that the wiper and arm combination cover over the windshield?
Answers
The area of the region that the wiper covers is 640.315 inches²
What is the arc of a sector formula?This formula is used when θ is in radian. Arc Length = θ × (π/180) × r; where θ = Central angle subtended by the arc, and r = radius of the circle. This formula is used when θ is in degrees.
Given here: A car windshield wiper and arm is 26 inches long and rotates at an angle of 108.6°.
A = (θ/360°) × πr²
θ is the sector angle subtended by the arcs at the center (in degrees), r is the radius of the circle. If the subtended angle θ is in radians, the area is given by, A = 1/2 × r² × θ.
A=108.6/360 ×3.14×26²
=0.30166×3.14×676
=640.315 inches²
Learn more about Area here:
https://brainly.com/question/14200825
#SPJ1
A total of 150 students voted for the class president.Bianca got 43 votes and Carlos recieved 38% of the votes. Which student recieved more votes how many more? Please help me This is due tomorrow
Answers
Answer:
Carlos Got more votes.
Step-by-step explanation:
If you do the math and find out what 38% of 150 is then you will have your answer
a.what is the value of this expression (5•7-2²•9+4³) divided by 9 b.Simplify the expression using the distributive property and combining like terms -8x(2x)+5(2x-12)+(-2)(5y-2)+(-3)(3y)
Answers
Answer:
A. 7
B.−16x^2+10x−19y−56
Explanation:
A. In the first attachment
B. In the second attachment


3. A man bought a car for $60 320. After using it for 2 years he decides to trade in the car. The company estimated a depreciation of 10% for the first year of its use and a further 15% on its reduced value for the second year.(a) Calculate the value of the car after two years.(b) Express the value of the car after two years as a percentage of the original value.
Answers
Answer:
a. £46144.8
b. ?
Step-by-step explanation:
Use Matlab to plot the function f(x) = - 4x² + sin(5x) and its derivative on the same plot for x between -10 and 10, in steps of 0.5 with appropriate legend and axis labels (use a dashed red line for f(x) and a solid blue line for its derivative). The derivative of f(x) is: (-4x² + sin(57x)) = - 8x + 5π cos(5x) dx Also, create an output file named "results.txt" and write x, f(x) and its derivative into the file. Use 2 decimal places. X f(x) df/dx
Answers
To plot the function f(x) = -4x^2 + sin(5x) and its derivative, and to save the results in a file named "results.txt" with 2 decimal places.
You can use the following MATLAB code:
```matlab
x = -10:0.5:10; % Generate x values
f = -4*x.^2 + sin(5*x); % Calculate f(x)
df_dx = -8*x + 5*pi*cos(5*x); % Calculate the derivative
% Saving results to file
output = [x', f', df_dx'];
dlmwrite('results.txt', output, 'delimiter', '\t', 'precision', '%.2f');
1. First, we define the range of x values using the vector `-10:0.5:10` to cover the desired interval with a step size of 0.5.
2. Next, we calculate the values of f(x) and its derivative using the defined mathematical expressions.
3. We then plot the function and its derivative using the `plot` function. The red dashed line represents f(x), and the blue solid line represents its derivative.
4. To save the results, we create a matrix `output` that concatenates the x values, f(x), and the derivative column-wise.
Learn more about decimal places here: brainly.com/question/20563248
#SPJ11
Box A is 12 ounces and cost 1.92 box B is 18 ounces and cost 3.42 which box will give Micah more for her money and by how much?
Answers
Answer:
box b 0.03
Step-by-step explanation:
i divided and got 1 ounces each

Determine the equation of the circle graphed below.

Answers
The equation of the circle graphed below is (x - 1)² + (y - 1)² = 4.
To determine the equation of a circle, we need to know the coordinates of its center and the radius. The general equation of a circle with center (h, k) and radius r is given by:
(x - h)² + (y - k)² = r²
where (x,y) are the coordinates of any point on the circle. The equation shows that the distance between any point (x,y) on the circle and the center (h,k) is always equal to the radius r.
To determine the equation of the circle graphed below, we need to identify the coordinates of its center and the radius. One way to do this is to use the distance formula between two points. We can choose any two points on the circle and use their coordinates to find the distance between them, which is equal to the diameter of the circle. Then, we can divide the diameter by 2 to find the radius.
To find the radius, we can choose any point on the circle and use the distance formula to find the distance between that point and the center. We can use the point (5,1), which is on the right side of the circle. The distance between (5,1) and (1,1) is 4 units, which means that the radius is 2 units.
Substituting the values of (h,k) and r in the general equation of the circle, we get:
(x - 1)² + (y - 1)² = 4
To know more about circle here
https://brainly.com/question/483402
#SPJ1
A rectangle has sides measuring (2x 7) units and (5x 9) units. Part A: What is the expression that represents the area of the rectangle? Show your work. (4 points) Part B: What are the degree and classification of the expression obtained in Part A? (3 points) Part C: How does Part A demonstrate the closure property for polynomials? (3 points).
Answers
If rectangle has sides measuring (2x +7) units and (5x +9) units then expression that represents the area of the rectangle is \(10x^2+53x+63\) and degree of this expression is 2 and we proved that it satisfy closure property .
what is a rectangle?A quadrilateral with four right angles is called rectangle .
Given that sides are (2x+7) and (5x+9)
Hence area of rectangle can be calculated as
\((2x+7)(5x+9)\\\\2x(5x+9)+7(5x+9)\\\\10x^2+18x+35x+63\\\\10x^2+53x+63\\\)
Now we can see that this is a second degree polynomial
We got polynomial \(10x^2+53x+63\) by multiplying two polynomial (2x+7) and (5x+9) hence it's closure property .
If rectangle has sides measuring (2x +7) units and (5x +9) units then expression that represents the area of the rectangle is \(10x^2+53x+63\) and degree of this expression is 2 and we proved that it satisfy closure property .
To learn more about rectangle visit :https://brainly.com/question/19819849
a rectangular lawn of sides 400m and 300m is surrounded by a path of width 3 m . find the area of path
Answers
Answer:
2109 meter squared
Step-by-step explanation:
\(Area \: of \: path \\ = (400+3)(300+3)-400 \times 300 \\ = 403 \times 303 - 120000 \\ = 122,109 - 120000 \\ = 2109 \: {m}^{2} \)
find the value of the discriminant. determine the number and type of solutions of the following quadratic equation without solving.
-6x^2+7x+3=0
Answers
Answer:
2 real and irrational roots
Step-by-step explanation:
given a quadratic equation in standard form
ax² + bx + c = 0 ( a ≠ )
then the nature of the roots can be determined using the discriminant
Δ = b² - 4ac
• if b² - 4ac > 0 then 2 real and irrational roots
• if b² - 4ac > 0 and a perfect square then 2 real and rational roots
• if b² - 4ac = 0 then 2 real and equal roots
• if b² - 4ac < 0 then 2 complex roots
- 6x² + 7x + 3 = 0 ← is in standard form
with a = - 6 , b = 7 , c = 3
b² - 4ac = 7² - (4 × - 6 × 3) = 49 - (- 72) = 49 + 72 = 121
since b² - 4ac > 0 then the equation has 2 real and irrational roots
Quadratic equation -
\(\: \:\:\:\: \small \underline{ \boxed{ \sf{ -6x^2 +7x+3 =0}}}\\\)
Where-
a =-6b=7c =3To find the Discriminant of this equation is given by -
\(\longrightarrow\underline\purple{\boxed{\pmb{D = b^2-4ac}}}\)
On substituting the values -
\( \: \:\:\:\: \longrightarrow\sf { D = \bigg(7\bigg)^2 - 4\times -6\times 3}\\\)
\( \: \:\:\:\: \longrightarrow\sf { D = 49+72}\\\)
\( \: \:\:\:\: \longrightarrow\pmb{ \underline{\purple{D =121}}}\\\)
Since, D>0 hence, this equation has two distinct real roots.
With this diagram, what could be the values of q and r ?
=147
q
=
14
7
, =−2.05
r
=
-
2.05
=0
q
=
0
, =−204
r
=
-
20
4
=3
q
=
3
, =−65
r
=
-
6
5
=−23
q
=
-
2
3
, =8

Answers
Answer:
the third one i belive so
Step-by-step explanation:
it makes more scence
Find the nth and 1525th term for each of the following sequences
a.6, 4.8, 3.6, 2.4, 1.2, …
b.13, 11, 9, 7, 5,
3. Given the explicit formula for an arithmetic sequence find the first five terms and the term named in the problem.
nth = 65 − 100n. Find 39th term (To find the nth term, replace the n with 1, 2, 3, 4, 5 and 39)
Example : 1st term = 65 - 100(1) = -35
Answers
The given sequence is 6, 4.8, 3.6, 2.4, 1.2, ...
To find the nth term of this sequence, we can observe that each term is obtained by multiplying the previous term by 0.8. Therefore, the common ratio between the terms is 0.8.
To find the nth term, we can use the formula: an = \(a1 * r^{n-1)},\) where an is the nth term, a1 is the first term, r is the common ratio, and n is the term number.
For this sequence, a1 = 6 and r = 0.8.
For the 1st term (n = 1): a1 = 6
For the 2nd term (n = 2): a2 =\(6 * 0.8^{(2-1)}\) = 4.8
For the 3rd term (n = 3): a3 =\(6 * 0.8^{(3-1)}\) = 3.84
For the 4th term (n = 4): a4 = \(6 * 0.8^{(4-1)}\)= 3.072
For the 5th term (n = 5): a5 =\(6 * 0.8^{(5-1)}\) = 2.4576
Therefore, the nth term for this sequence is an = 6 * 0.8^(n-1), and the 1525th term would be a1525 = \(6 * 0.8^{(1525-1)}.\)
The given sequence is 13, 11, 9, 7, 5, ...
To find the nth term of this sequence, we can observe that each term is obtained by subtracting 2 from the previous term. Therefore, the common difference between the terms is -2.
To find the nth term, we can use the formula: an = a1 + d * (n-1), where an is the nth term, a1 is the first term, d is the common difference, and n is the term number.
For this sequence, a1 = 13 and d = -2.
For the 1st term (n = 1): \(a1 = 13\)
For the 2nd term (n = 2): \(a2 = 13 + (-2) * (2-1) = 11\)
For the 3rd term (n = 3): \(a3 = 13 + (-2) * (3-1) = 9\)
For the 4th term (n = 4): \(a4 = 13 + (-2) * (4-1) = 7\)
For the 5th term (n = 5): \(a5 = 13 + (-2) * (5-1) = 5\)
Therefore, the nth term for this sequence is an = \(13 + (-2) * (n-1\)), and the 1525th term would be \(a1525 = 13 + (-2) * (1525-1).\)
The given explicit formula for the arithmetic sequence is nth = 65 - 100n.
To find the first five terms, we substitute n = 1, 2, 3, 4, and 5 into the formula:
For the 1st term (n = 1): \(a1 = 65 - 100 * 1 = -35\)
For the 2nd term (n = 2): \(a3 = 65 - 100 * 3 = -235\)
For the 3rd term(n = 3): \(a3 = 65 - 100 * 3 = -235\)
For the 4th term (n = 4): \(a4 = 65 - 100 * 4 = -335\)
For the 5th term (n = 5): \(a5 = 65 - 100 * 5 = -435\)
Therefore, the first five terms of this arithmetic sequence are: -35, -135, -235, -335, -435.
To find the 39th term, we substitute n = 39 into the formula:
\(a39 = 65 - 100 * 39 = 65 - 3900 = -3835\)
Therefore, the 39th term of this arithmetic sequence is -3835.
For more questions on sequence
https://brainly.com/question/7882626
#SPJ11
What is the quotient when 1.272 divided by 0.003?
Answers
Answer:
The answer is 424.
1. Nasim thinks of a number.
When he multiplies his number by 5 and subtracts 16 from the result, he gets the same
answer as when ads 10 to his number and multiplies that result by 3.
Find the number Nasim is thinking of.
Answers
Step-by-step explanation:
5x-16 = 3 (10+x)
=> x= 23
Solve the equation for y.
12 13 y + 12 = 1/3 - 20
-32
-80
-320
320
Answers
Answer:
No
Step-by-step explanation:
sorry iiiiiimmm bad at math
Reduce 240 in the ratio 2:3
Answers
Answer:
96 , 144
Step-by-step explanation:
Ratio = 2 : 3
2x + 3x = 240
5x = 240
x = 240/5
x = 48
2x = 2*48 = 96
3x = 3*48 = 144
evaluate the iterated integral by changing to cylindrical coordinates. 2 −2 4 −4 √16 − x2 (x2 y2)3/2 dy dx dz −√16 − x2
Answers
The iterated integral by changing to cylindrical coordinates 2 −2 4 −4 √16 − x2 (x2 y2)3/2 dy dx dz −√16 − x2 is 128π.
To evaluate the iterated integral using cylindrical coordinates, first, we need to change the given rectangular coordinates (x, y, z) to cylindrical coordinates (ρ, φ, z). In cylindrical coordinates, x = ρcosφ, y = ρsinφ, and z = z. The Jacobian for the transformation is |J| = ρ. The given integral can be rewritten as:
∫(φ=0 to 2π) ∫(ρ=0 to 4) ∫(z=-√16-ρ² to √16-ρ²) (ρ²)³/2 * ρ dz dρ dφ
Now, we can evaluate the integral step by step:
1. Integrate with respect to z:
∫(φ=0 to 2π) ∫(ρ=0 to 4) [(z * ρ³) | (z = -√16-ρ²) to (z = √16-ρ²)] dρ dφ
2. Integrate with respect to ρ:
∫(φ=0 to 2π) [(1/4 * ρ⁴) | (ρ = 0) to (ρ = 4)] dφ
3. Integrate with respect to φ:
[(1/4 * 4⁴) * (φ | φ=0 to 2π)] = (256/4) * 2π = 128π
So the value of the iterated integral in cylindrical coordinates is 128π.
For more such questions on Iterated Integral.
https://brainly.com/question/29667432#
#SPJ11
PRE CALC PEOPLE HELP PLSSSSS
Find three additional polar representations of the point (2, 3π/4)
using −2 < < 2.
(r, ) = smallest value?
(r, ) = ?
(r, ) = largest value?
Answers
To find three additional polar representations of the point (2, 3π/4), we can add or subtract 2πk to the angle, where k is an integer. Using this method, we get:
(2, -5π/4) - subtract 2π
(2, 11π/4) - add 2π
(2, -3π/4) - subtract 2π
To find the smallest and largest values of the angle, we need to consider the interval −2π < θ < 2π. The given angle of 3π/4 lies in the second quadrant. Adding or subtracting 2π to this angle will give us angles in the third and fourth quadrants. Therefore, the smallest value of the angle is −3π/4, and the largest value is 5π/4. Thus, the polar representations are:
(2, 3π/4)
(2, -5π/4)
(2, 11π/4)
(2, -3π/4)
(2, 5π/4)
How to solve these? I would like explanation please

Answers
Step-by-step explanation:
9.
it is a rectangle. 18m × 4m = 72 m²
the paving costs $35 per m², and we have 72 m², so it does not take a genius to figure out what to do next ...
right : we multiply 35 by 72
35×72 = $2520
10.
how much volume is a liter ?
a liter fits into a cube of 10cm side length.
and 1 meter = 100 cm = 10×10cm.
so, 1 m³ = 10×10×10 = 1000 such cubes of 10cm side length = 1000 liters.
the pool is 5 m × 15 m × 1.5 m = 112.5 m³ = 112500 liters
we need 2 kg salt for every 10000 liters water, so we have how many units of 10000 liters in the pool ?
112500 / 10000 = 11.25
so, we need
11.25 × 2 = 22.5 kg salt
11.
12 seconds = 1/5 of a minute.
so, batman runs at 3 km / min (= 60×3 km/hour = 180 km/h - not possible in real life for any human being, but let's play ...) for 12 seconds = 1/5th of a minute, and so he runs 3km/5 = 600 meters in that time.
that means he has 2km - 600m = 1400m left to run in the 2 km race.
it takes him 1400/3000th of a minute (3000 m would take him the full minute)
1400 m × minute / 3000 m = 14/30 = 7/15 minutes
1/15th minute = 60 seconds / 15 = 4 seconds.
so, 7/15th of a minute = 7×4 seconds = 28 seconds.
the bionic woman runs the full 2000 m with 5 km / minute.
it takes her 2000/5000th of a minute
2000 m × minute / 5000 = 2/5th of a minute.
1/5th of a minute is 60 seconds / 5 = 12 seconds.
so, 2/5th of a minute is 12×2 = 24 seconds.
therefore, the bionic woman wins by 4 seconds (24 seconds vs. 28 seconds).
12.
there is enough food for 150 students for 5 days = 150×5 =750 "food units".
therefore, if there were only 100 students, the food would last 750/100 = 7.5 days.
and if the food runs out after 4 days it means there are
750/4 = 187.5 students (how much sense that makes to have half a student ...).
13.
x = the workload to be done
Michelle's work speed is x/6 days
Danielle's work speed is x/4 days
on each day working together they achieve
1× x/6 + 1× x/4 of the total work load.
that is
2x/12 + 3x/12 = 5x/12
so, they need 5x/12 × a days to finish the whole x.
5x/12 × a = x
5/12 × a = 1
5a = 12
a = 12/5 = 2.4 days to finish the whole work when working together.
NEED HELP GRAPHING I HAVE ALL THE ANSWERS JUST NEED A GRAPH
Find the slope and y-intercept of the following line.
Graph the line.
y = 5x-8
A. The slope is 5.
What is the y-intercept of the line? (0,-8)
Use the graphing tool to graph the line. Use the slope
and y-intercept when drawing the line.
Answers
Answer: See below for the graph
The graph is a straight line through (0,-8) and (1,-3)
======================================================
Further explanation:
You have the correct y intercept. This is where the graph crosses the y axis.
From this starting point, move up 5 units and to the right 1 unit. This motion of "up 5, right 1" is directly from the slope of 5 aka 5/1
slope = rise/run = 5/1
rise = 5 = how far you go up
run = 1 = how far you move to the right
So if we started at (0,-8) and moved up 5, right 1, then we would arrive at (1,-3)
Once these two points are plotted together, we can draw a straight line through them as you see below. I used GeoGebra to make the graph, but you could use Desmos (or similar) if you prefer.