Can you do questions 3, 6, 11, and 12 please? Please explain how you do them too...


Answers
Answer:
3. d = -1
6. x = 5
11. y = -1/6x+2
12. y = 9x-12
Step-by-step explanation:
Attached a picture showing the work for the problems, if you need any additional help, let me know.

Related Questions
12=15(z-1/5) does anybody know how to solve this
Answers
Answer:
-15
Step-by-step explanation:
Michelle has $8 and wants to buy a combination of dog food to feed at least two dogs at the animal shelter. A serving of dry food costs $1, and a serving of wet food costs $3. This system of inequalities models the scenario: x + 3y ≤ 8 x + y ≥ 2 Part A: Describe the graph of the system of inequalities, including shading and the types of lines graphed. Provide a description of the solution set. (4 points) Part B: Is the point (8, 2) included in the solution area for the system? Justify your answer mathematically. (3 points) Part C: Choose a point in the solution set and interpret what it means in terms of the real-world context. (3 points)
Answers
Part A: The shaded region represents the feasible region where both inequalities are satisfied simultaneously. It is below the line x + 3y = 8 and above the line x + y = 2.
Part B: The point (8, 2) is not included in the solution area.
Part C: The point (3, 1) represents one feasible solution that meets the constraints of the problem.
Part A: The graph of the system of inequalities consists of two lines and a shaded region. The line x + 3y = 8 is a solid line because it includes the equality symbol, indicating that points on the line are included in the solution set. The line x + y = 2 is also a solid line. The shaded region represents the feasible region where both inequalities are satisfied simultaneously. It is below the line x + 3y = 8 and above the line x + y = 2.
Part B: To determine if the point (8, 2) is included in the solution area, we substitute the x and y values into the inequalities:
8 + 3(2) ≤ 8
8 + 6 ≤ 8
14 ≤ 8 (False)
Since the inequality is not satisfied, the point (8, 2) is not included in the solution area.
Part C: Let's choose a point in the solution set, such as (3, 1). This point satisfies both inequalities: x + 3y ≤ 8 and x + y ≥ 2. In the context of the real-world scenario, this means that Michelle can buy 3 servings of dry food (x = 3) and 1 serving of wet food (y = 1) with her $8 budget. This combination of dog food allows her to feed at least two dogs at the animal shelter while staying within her budget. The point (3, 1) represents one feasible solution that meets the constraints of the problem.
For more such questions on feasible region
https://brainly.com/question/29084868
#SPJ8
how do I solve this?

Answers
Answer:
sinJ = \(\frac{12}{13}\)
Step-by-step explanation:
sinJ = \(\frac{opposite}{hypotenuse}\) = \(\frac{IK}{JK}\) = \(\frac{12}{13}\)
Suppose the linear approximation for a function f(x) at a = 3 is given by the tangent line y = −2x + 12. What are f(3) and f '(3)? f(3) = f '(3) = If g(x) =[f(x)]2 , find the linear approximation for g(x) at a = 3, L(x) = _____
Answers
The linear approximation for g(x) at a = 3 is L(x) = -24x + 108.
The equation of the tangent line to a function f(x) at a point x = a is given by: y = f(a) + f'(a)(x - a)
In this case, the linear approximation for f(x) at a = 3 is given by the tangent line:
y = -2x + 12
Comparing this to the equation of the tangent line, we have:
f(a) = -2a + 12 = -2(3) + 12 = 6
f'(a) = -2
Therefore, f(3) = 6 and f'(3) = -2.
To find the linear approximation for g(x) = [f(x)]^2 at a = 3, we can use the chain rule:
g'(x) = 2f(x)f'(x)
At a = 3, we have:
g(3) = [f(3)]^2 = 6^2 = 36
g'(3) = 2f(3)f'(3) = 2(6)(-2) = -24
The equation of the tangent line to g(x) at a = 3 is then: y = g(3) + g'(3)(x - 3)
Substituting in the values we found, we get:
y = 36 - 24(x - 3) = -24x + 108
Therefore, the linear approximation for g(x) at a = 3 is L(x) = -24x + 108.
For such more question on linear:
https://brainly.com/question/28732353
#SPJ11
What fraction is equivalent to 3/12?
A.12/48
B.1/4
C.18/60
D.24/96
Answers
plz answer only if u know ur correct

Answers
Answer:
1/2
Step-by-step explanation:
Answer:
Slope is 1/2
Step-by-step explanation:
Points (10,20) (30,30)
Y2-y1/x2-x1
30- 20/30-10
10/20
1/2
The circumference of a circle is 7π in. What is the area, in square inches? Express your answer in terms of π.
Answers
Answer:
\(\dfrac{49}{4}\pi=12.25\pi \; \sf in^2\)
Step-by-step explanation:
To find the area of the circle with a circumference of 7π inches, first need to find the radius of the circle.
The formula for the circumference of a circle is:
\(\boxed{C = 2 \pi r}\)
where r is the radius of the circle.
If the circumference of a circle is 7π inches, substitute C = 7π into the formula and solve for the radius, r:
\(\begin{aligned}\implies 2\pi r&=7\pi\\\\\dfrac{2\pi r}{2\pi}&=\dfrac{7\pi}{2\pi}\\\\r&=\dfrac{7}{2}\; \sf in\end{aligned}\)
The formula for the area of a circle is:
\(\boxed{A=\pi r^2}\)
where r is the radius of the circle.
Substitute the found value of r into the area formula to find the area of the circle:
\(\begin{aligned}\implies \sf Area&=\pi r^2\\\\&=\pi \cdot \left(\dfrac{7}{2}\right)^2\\\\&=\pi \cdot \left(\dfrac{7^2}{2^2}\right)\\\\&=\pi \cdot \left(\dfrac{49}{4}\right)\\\\&=\dfrac{49}{4}\pi \\\\&=12.25\pi \sf \; in^2\end{aligned}\)
Therefore, the area of the circle in terms of π is (49/4)π square inches.
If someone could help that would be so helpful

Answers
The center of the circle is (-3, -1). The new center of the new circle is (-3, -5). The new equation of the circle is:
(x -3)² + (y - 5)² = 10².
What is equation of circle?With a circle's center and radius, one may mathematically describe a circle using the equation of a circle. A circle's equation is distinct from the formulae used to determine a circle's area or circumference. Many circles-related coordinate geometry issues employ this equation. We require the circle's equation in order to represent a circle on the Cartesian plane. If we are aware of the radius's length and the circle's centre, we can draw a circle on a sheet of paper. The same is true for drawing circles on a Cartesian plane if we are aware of the center's and radius's coordinates.
The general equation of the circle is given as:
(x - h)² + (y - k)² = r²
Where, h and k are the coordinates of the center.
The given equation is (x -3)² + (y - 1)² = 10²
The center is (-3, -1).
Given that, the circle is shifted 4 up.
The y-coordinate is:
y - (1 + 4) = y - 5
Thus, the new equation of the circle is:
(x -3)² + (y - 5)² = 10²
The new center of the new circle is (-3, -5).
Hence, the center of the circle is (-3, -1). The new center of the new circle is (-3, -5). The new equation of the circle is:
(x -3)² + (y - 5)² = 10²
Learn more about equation of circle here:
https://brainly.com/question/23799314
#SPJ1
Two line segments are parallel to each other. The first line segment has
endpoints (2, 5) and (8, 8). The second line segment has endpoints (4, 0) and (8,
y). What is the value of y?
A. -2
B. 2
C. 4
D. -4
Answers
Step-by-step explanation:
b.2 is the correct answer
Learn at brainlyHow many solutions does the equation have?-4x+6=6x-2
Answers
Answer:
\( - 4x + 6 = 6x - 2 \\ 6x + 4x = 6 + 2 \\ 10x = 8 \\ x = \frac{8}{10} = \frac{4}{5} \\ x = 0.8 \)
Please help solve this equation. -3(5w-3y-2)
Answers
Answer:
-15w+9y+6
Step-by-step explanation:
I think that you are asking to simplify the expression. An equation has an equal sign and I do not see one.
We need to distribute the -3 to everything inside of the parentheses.
A negative times a negative is a positive.
A negative times a positive is a negative.
-3(5w-3y-2)
-3(5w) -3(-3y) -3(-2)
-15w + 9y + 6
Hi!
To simplify this, use the Distributive Property:
\(\tt{a(b+c)=ab+ac}\) | Basically, we distribute a so that it gets multiplied by b and c.Now, let's simplify the given expression:
\(\dashrightarrow\sf{-3(5w-2y-2)}\)
Like the property said, We should distribute -3 so that it's multiplied by each term:
\(\bullet\dashrightarrow\sf{-15w+9y+6}\)
Therefore,
\(\bullet\dashrightarrow\stackrel{\heartsuit}{\boxed{\boxed{\boldsymbol{-15w+9y+6}}}}}\dashleftarrow\bullet\)
Good luck.- stargazing :')
What is the value of this product

Answers
Answer:
The value of the product is 2²
what is the solution of the equation 4x + 12 = 48
Answers
Answer:
x =9
Step-by-step explanation:
48-12=36
4x=36
divide by 4
x=9
Answer: A) x=9
48-12=36.
36/4=9
More detailed explanation:
4x+12=48
-12 -12
4x = 36
/4 /4
x = 9
Step-by-step explanation:
subtract 12 from both sides , then divide both sides by 4
Find the area of the shaded regions. Give your answer as a
completely simplified exact value in terms of л (no
approximations).
D
6
(1209
3 cm
A
0
B
4 cm
C
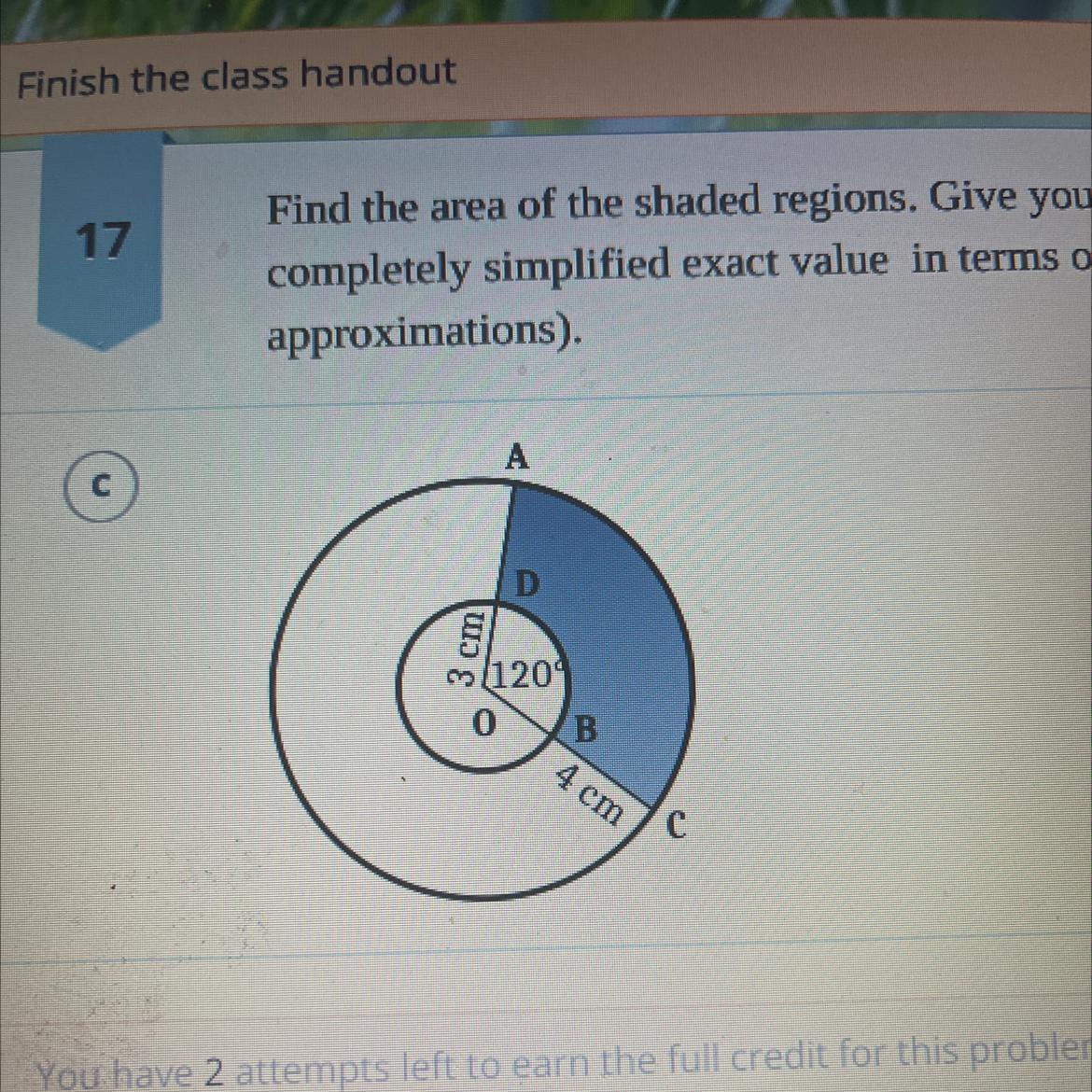
Answers
The area of the shaded region is 41.86 cm².
Given are two concentric circles with radii 7 cm and 3 cm and a common central angle of 120°, we need to find the area which shown shaded.
So, to find the area of the same region we will find the area of the bigger sector and the smaller sector the will subtract the smaller sector to bigger sector.
So, area of a sector = central angle / 360° × π × radius²
So, area of the required region = (120° / 360° × 3.14 × 49) - (120° / 360° × 3.14 × 9)
= 1/3 × 3.14 (49-9)
= 41.86
Hence the area of the shaded region is 41.86 cm².
Learn more about area of a sector click;
https://brainly.com/question/29055300
#SPJ1
If the measures of the angles in the following triangle were listed in increasing order, which measure would be second? (2x+24) ° (4x+43) ° (x^2+1) °
Answers
Answer:
x²+1 is the second
Step-by-step explanation:
2x+24=40°
4x+43=75°
x²+1=65°
(2x+24) + (4x +43) + (x²+1)=180
x²+6x+68=180
x1=-14
x2=8
since there's no negative angle, we'll use x=8
help asap if you can pls an thank u!!!!!!!

Answers
The value of angle S is 53°
What is exterior angle theorem?Exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of two remote interior angles.
With this theorem we can say that
7x+2 = 4x+13+19
collecting like terms
7x -4x = 13+19-2
3x = 30
divide both sides by 3
x = 30/3
x = 10
Since x = 10
angle S = 4x+13
angle S = 4(10) +13
= 40+13
= 53°
Therefore the measure of angle S is 53°
learn more about exterior angle theorem from
https://brainly.com/question/17307144
#SPJ1
Find a functiony x( )whose second derivative is y x x ( ) 12 2 , given f x x ( ) 5 is tangent to y x x ( ) at 1.
Answers
The tangent of y(x) at x = 1 is y'(1) = 4 + C₁, and the value of f(1) is 5, we can solve for C₁ to get C₁ = 1. Therefore, the function y(x) = x⁴ / 4 + x + C₂, where C₂ is another constant.
The given equation is f (x) = 5, and it is the tangent of the function y = x³ / 3 at x = 1.To get y = x (x² / 2 + C), we integrate the second derivative of y with respect to x.∫(d²y/dx²)dx = ∫(12x²)dx => y = 4x³ + C₁ Solve for C₁ by applying the point-slope equation at the point x = 1:f(1)
= 5
= y(1)
= 4(1)³ + C₁
=> C₁ = 1Therefore, the equation of y is: y = 4x³ + 1.For a more in-depth and better explanation, here are 150 words: A second derivative represents the rate of change of the first derivative with respect to x.
Therefore, if we have a second derivative of y with respect to x, we can integrate it twice to get a function of y with respect to x. Given y''(x) = 12x², we can integrate it once to obtain y'(x) = 4x³ + C₁, where C₁ is a constant. We integrate y'(x) once again to get y(x) = x⁴ / 4 + C₁x + C₂, where C₂ is another constant. Now, to find C₁ and C₂, we need to use the fact that the function f(x) = 5 is tangent to y(x) at x = 1.
Learn more about derivative:
https://brainly.com/question/29144258
#SPJ11
The tangent of y(x) at x = 1 is y'(1) = 4 + C₁, and the value of f(1) is 5, we can solve for C₁ to get C₁ = 1. Therefore, the function y(x) = x⁴ / 4 + x + C₂, where C₂ is another constant.
The given equation is f (x) = 5, and it is the tangent of the function
y = x³ / 3 at x = 1.
To get y = x (x² / 2 + C),
we integrate the second derivative of y with respect to x.
∫(d²y/dx²)dx = ∫(12x²)dx
=> y = 4x³ + C₁
Solve for C₁ by applying the point-slope equation at the point
x = 1:f(1)
= 5
= y(1)
= 4(1)³ + C₁
=> C₁ = 1Therefore, the equation of y is: y = 4x³ + 1
.For a more in-depth and better explanation, here are 150 words: A second derivative represents the rate of change of the first derivative with respect to x.
Therefore, if we have a second derivative of y with respect to x, we can integrate it twice to get a function of y with respect to x.
Given y''(x) = 12x²,
we can integrate it once to obtain
y'(x) = 4x³ + C₁, where C₁ is a constant.
We integrate y'(x) once again to get
y(x) = x⁴ / 4 + C₁x + C₂, where C₂ is another constant.
Now, to find C₁ and C₂, we need to use the fact that the function
f(x) = 5 is tangent to y(x) at x = 1.
Learn more about derivative:
brainly.com/question/29144258
#SPJ11
what is 16% of 4kilogram
Answers
Answer:
0.64 kilogram
Step-by-step explanation:
Given the figure below, find the values of x and z.

Answers
Answer:
make me brainlaiest.....

Answer:
The value of x = 5
The value of z = 107
Step-by-step explanation:
=> (6x+43)° +107° = 180° { linear pair }
=> 6x+43 +107 = 180
=> 6x + 150 = 180
=> 6x = 180-150
=> x = 30/6
=> x = 5
Now solve for z ,
107 = z { Vertically opposite angle }
A box has the shape of a rectangular prism with height 28 cm. If the height is increased by 0.6 cm.
i have nothing to do so add my roblox acccount i might be inactive alot
user- dennisalvez1_alt
Answers
Answer:
The surface area of the box increase by 0.2P (the perimeter of the base multiplied by 0.2)
Step-by-step explanation:
we know that
The surface area of the rectangular prism is equal to where B is the area of the base P is the perimeter of the base h is the height of the prism If the height is increased by 0.2 then The surface area of the box increase by 0.2P (the perimeter of the base multiplied by 0.2)
Answer:
who even plays roblox anymore
Step-by-step explanation:
4. How many 5 -digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Answers
There are 336 different 5-digit telephone numbers that can be constructed using the digits 0 to 9, starting with "67" and with no repeated digits.
To answer your question, we need to find the number of ways to arrange the remaining three digits after "67" is fixed.
Since we cannot repeat any digit, the first digit has 8 possibilities (0 to 9 except for 6 and 7).
the second digit has 7 possibilities, and the third digit has 6 possibilities.
To find the total number of arrangements, we multiply the number of possibilities for each digit together:
8 × 7 × 6 = 336.
Therefore, there are 336 different 5-digit telephone numbers that can be constructed using the digits 0 to 9, starting with "67" and with no repeated digits.
To know more about numbers visit :
https://brainly.com/question/32585587
#SPJ11
Maximize the objective function P = 3x + 5y for the given constraints

Answers
A 20 oz. smoothie cost $3.59. What is the unit price rounded to the nearest cent?
Answers
turn 311/34 to a mixed number
Answers
Step 1 - Find Whole Number
Calculate out how many times the denominator goes into the numerator. To do that, divide 311 by 34 and keep only what is to the left of the decimal point: 311 / 34 = 9.1471 = 9
Step 2 - Find New Numerator
Multiply the answer from Step 1 by the denominator and deduct that from the original numerator. 311 - (34 x 9) = 5
Step 3 - Get Solution
Keep the original denominator and use the answers from Step 1 and Step 2 to get the answer. 311/34 as a mixed number is
9
5/34
If x / 2y = 0.4 , A / 5B = 0.25 Then A + y / 5 =…....
Answers
Answer:
\( \frac{x}{2y} = \frac{4}{10} \\ 8y = 10x \\ y = \frac{10x}{8} - - - - - 1 \\ \\ \frac{a}{5b} = \frac{25}{100} \\ \frac{a}{5b} = \frac{1}{4} \\ 4a = 5b \\ a = \frac{5b}{4} - - - 2 \\ \\ so \: \: \frac{a + y}{5} \\ = (a + y) \times \frac{1}{5} \\ = ( \frac{5b}{4} + \frac{5x}{4} ) \times \frac{1}{5} \\ = \frac{5b + 5x}{4} \times \frac{1}{5} \\ = \frac{5(b + x)}{4} \times \frac{1}{5} \\ = \frac{b + x}{4} \\ \\ so \: \: \: \frac{a + y}{5} = \frac{b + x}{4} \)
Given that \(\frac{x}{2y} = 0.4 \ and \frac{A}{5B} = 0.25.\) The value of equation \(\ \frac{A+y}{5} = \frac{x+10B}{40}\)
An equation is a mathematical statement with an 'equal to' symbol between two expressions that have equal values. The expressions may contain any constants, variables and algebraic operators.
Given the equations,
equation 1:
\(= \frac{x}{2y} = 0.4 = \frac{4}{10} \\\\= 10x = 80y \\\\= x = 8y\\\\=y = \frac{x}{8}\)
equation 2:
\(\frac{A}{5B} = 0.25 = \frac{25}{100} = \frac{1}{4}\\ \\=4A = 5B\\\\=A = \frac{5B}{4}\)
We need to find \(\frac{A + y}{5}\),
putting the value of A and y in the equation,
\(= \frac{A + y}{5}\\\\=\frac{\frac{x}{8}+\frac{5B}{4} }{5} \\\\= \frac{x+10B}{40}\)
Learn more about equations here
https://brainly.com/question/33622350
#SPJ2
An aquarium 4 ft long, 2 ft wide, and 4 ft deep is full of water. (recall that the weight density of water is 62. 5 lb/ft3. ) (a) find the hydrostatic pressure (in lb/ft2) on the bottom of the aquarium
Answers
The hydrostatic pressure on the bottom of the aquarium is 8044 lb/ft2.
The hydrostatic pressure on the bottom of the aquarium can be found using the formula:
P = ρgh
where P is the pressure, ρ is the density of the fluid (water), g is the acceleration due to gravity, and h is the depth of the fluid.
Here, ρ = 62.5 lb/ft3, g = 32.2 ft/s2 (acceleration due to gravity), and h = 4 ft (depth of water).
Thus, the hydrostatic pressure on the bottom of the aquarium is:
P = (62.5 lb/ft3) x (32.2 ft/s2) x (4 ft)
= 8044 lb/ft2
Therefore, the hydrostatic pressure on the bottom of the aquarium is 8044 lb/ft2.
Learn more about hydrostatic pressure here:
https://brainly.com/question/14810152
#SPJ11
•Sequences and functions
( 10 points )
Please help me loves with the answer and understanding
•Please actually help me out I want to better understand this
•trolls will be reported

Answers
when it comes to geometric progression the common ratio (r) must be the same.
to find r, use this formula :
r = T2/T1
= 12/72 = 1/6
= 2/12 = 1/6
explain how you could use the construction tool or compass and straightedge to create a line segment that is twice as long as AB.
(a 1 inch segment line to a two inch segment line)
Answers
You can use a compass and straightedge to construct a line segment that is twice as long as AB, going from a 1-inch segment to a two-inch segment
To construct a line segment that is twice as long as AB (a 1-inch segment) using a compass and straightedge, you can follow these steps:
Start by drawing line segment AB with a length of 1 inch.
Place the point of the compass on point A and extend the compass to any convenient distance.
Without changing the compass width, draw an arc that intersects line segment AB. Label the intersection point as C.
With the compass width still unchanged, place the point of the compass on point C and draw another arc intersecting the previously drawn arc. Label the new intersection point as D.
Use a straightedge to draw a line segment from point A to point D. This line segment, AD, will be twice the length of line segment AB.
By following these steps, you can use a compass and straightedge to construct a line segment that is twice as long as AB, going from a 1-inch segment to a two-inch segment.
For more questions on construct
https://brainly.com/question/30408163
#SPJ8
Write the equation of a line in point slope form that passes through the point (5,9) and
has a slope of -3
Answers
Answer:
Write the point slope form of the equation of the line that passes through the points (5,-9).
---
slope = m = (1--9)/(-6-5) = 10/-11 = -10/11
-------------------
Form:: y = mx + b
Solve for "b"::
-9 = (-10/11)5 + b
-------
Step-by-step explanation:
ur really pretty btw :p
Gabby took a math quiz last week. There were 28 problems on the quiz and Gabby answered 25% of them correctly. How many problems did Gabby get correct? problems
Answers
Answer:
7
Step-by-step explanation:
25% of 28 =
= 0.25 × 28
= 7
Answer: 7
25 percent becomes 0.25 when u multiply it with 28 it equals to 7 so 7 is the answer