Answers
Answer:
∠EBF = 51°
∠DBE = 17°
∠ABF = 141°
∠EBA = 90°
∠DBC = 107°
∠DBF = 68°
Step-by-step explanation:
Hope this helps
Answer:
1.
a. m<EBF = 90 - 39 = 51
b. m<EBA = 90
c. m<DBE = 90 - 73 = 17
d. m<DBC = 90 + 17 = 107
e. m<ABF = 90 + 51 = 141
f. m<DBF = 17 + 51 = 68
2.
<ABD, <DBE, <EBF, <FBC, <DBF
3.
<ABF, <DBC
4.
<ABE, <EBC
Related Questions
D(5, 7), E(4, 3), and F(8, 2) form the vertices of a triangle. What is mZDEF?
Answers
Answer: \(m\angle DE F=90^{\circ}\)
Step-by-step explanation:
The slope of \(DE\) is \(\frac{7-3}{5-4}=4\).
The slope of \(EF\) is \(\frac{3-2}{4-8}=-\frac{1}{4}\).
Thus, \(DE \perp EF\), meaning \(m\angle DE F=90^{\circ}\).
Find the volume of the solid formed by rotating the region inside the first quadrant enclosed by
y=x4 and y=125x
Answers
The volume of the solid formed by rotating the region inside the first quadrant enclosed by y=x⁴ and y=125x is 138438\(\pi\).
Let,
f(x) = 125x
g(x) = x⁴
Intersection points will be,
x⁴ = 125x
x = 0 , 3.3437
Volume V = \(\pi\)\(\int\limits^{3.34}_0{(125x)^{2} - x^8 } \, dx\)
=\(\pi\)\(\int\limits^{3.34}_0 {15625x^2-x^8} \, dx\)
=\(\pi\)[15625x³/3 - x⁹/9]₀³
=\(\pi\)[140625 - 2187]
= 138438\(\pi\)
The volume of the solid formed by rotating the region inside the first quadrant enclosed by two curves can be found using the method of cylindrical shells. This method involves cutting the solid into thin cylindrical shells and finding the volume of each shell. The sum of the volumes of the shells is equal to the volume of the solid.
To learn more about volume of the solid click on,
https://brainly.com/question/22807624
#SPJ4
calculate the sales tax
and total cost.
price: $275.25
tax rate: 7%
Answers
The total cost is $294.52
$275.25 x 0.07 = $19.27
$275.25 x 1.07 = $294.52 :)
Which expressions are less than 7/8? Choose2 answers 7/8 x 9/19 7/8 x 3/4 7/8 x 9/9 7/8 x 4/3
Answers
The two expressions that are less than 7/8 are 7/8 x 9/19 and 7/8 x 3/4.
To determine which expressions are less than 7/8, we can compare them individually to 7/8 and evaluate their values.
Let's consider each expression one by one:
7/8 x 9/19:
To compare this expression to 7/8, we multiply the fractions:
(7/8) x (9/19) = 63/152.
Since 63/152 is less than 7/8, this expression is less than 7/8.
7/8 x 3/4:
Multiplying the fractions:
(7/8) x (3/4) = 21/32.
Since 21/32 is less than 7/8, this expression is less than 7/8.
7/8 x 9/9:
The fraction 9/9 simplifies to 1, so the expression becomes:
(7/8) x 1 = 7/8.
Since 7/8 is equal to 7/8 (not less than), this expression is not less than 7/8.
7/8 x 4/3:
Multiplying the fractions:
(7/8) x (4/3) = 28/24.
We can simplify 28/24 to 7/6.
Since 7/6 is greater than 7/8, this expression is not less than 7/8.
Therefore, the two expressions that are less than 7/8 are 7/8 x 9/19 and 7/8 x 3/4.
for such more question on expressions
https://brainly.com/question/12270624
#SPJ8
differenciate the Function 1/ X3
Answers
Step-by-step explanation:
To differentiate the function f(x) = 1/x^3, we can use the power rule of differentiation. Here's the step-by-step process:
Write the function: f(x) = 1/x^3.
Apply the power rule: For a function of the form f(x) = x^n, the derivative is given by f'(x) = nx^(n-1).
Differentiate the function: In our case, n = -3, so the derivative is:
f'(x) = -3 * x^(-3-1) = -3 * x^(-4) = -3/x^4.
Therefore, the derivative of the function f(x) = 1/x^3 is f'(x) = -3/x^4.
helppppppppppppppppppppppppppppppppppppppppppppppppppppp


Answers
Answer:
first second sum
5 2 7
7 -3 4
-10 6 -4
second picture
D, C, B, A
Step-by-step explanation:
Answer:
Step-by-step explanation:
First second sum
5 2 7
7 -3 4
-10 6 -4
Second question
d,c,a,b
Help!! Factor the common factor out of each expression

Answers
Therefore , the solution of the given problem of equation comes out to be factor is (5b)(-5b+3).
What is the equation?A formula for connecting two statements using the equal sign (=) to denote equivalence is known as a mathematical equation. A mathematical equation in algebra is a statement that proves the equality of two mathematical expressions. For instance, the formula 3x + 5 = 14 places an equal sign between the variables 3x + 5 and 14. The mathematical relationship between the two sentences on either side of a letter is established. Most of the time, the symbol serves as both the one and only variable. for instance, 2x – 4 = 2.
Here,
the two numbers' primary factors are as follows:
-25\(b^{2}\) + 15b
Common prime factors can be multiplied to determine the GCF:
=> -25\(b^{2}\) = -(5)(5) * \(b^{2}\)
=> 15b = (5)(3)b
The expression can be factored in the following fashion because the GCF is 5b:
=> -(5)(5) * \(b^{2}\) + (5)(3)b
=> (5b)(-5b+3)
Therefore , the solution of the given problem of equation comes out to be factor is (5b)(-5b+3).
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
What is -1 - 9
Solve for 2x-4y =20
X=4
Answers
Answer:
So -1-9= -10
And if x =4 then 2(4)-4y=20
Y= -3
Step-by-step explanation:
2(4)-4y=20
8-4y=20
-4y=12
y=-3
Answer:
-1 - 9 = -10 &
y = -3
Step-by-step explanation:
2x - 4y = 20
2(4) - 4y = 20
8 - 4y = 20
-4y = 12
y = -3
good luck, i hope this helps :)
Can someone help please?
ASAP

Answers
Answer:
Angle A = tan^-1(11/5)
Angle C = 90 - tan^-1(11/5)
AC = sqrt(146)
Step-by-step explanation:
As this is a right triangle, we can apply the Pythagorean theorem a^2 + b^2 = c^2, where c is the hypotenuse while a and b are the legs, to solve for AC.
11^2 + 5^2 = AC^2
121 + 25 = AC^2
146 = AC^2
sqrt(146) = AC^2
Next, to find angle A, we can use one of the trigonometric functions. Let’s use tangent for simplicity. Tangent of an angle is “opposite divided by adjacent”. If we set the angle to A, opposite is side BC and the adjacent is side AB. Thus, tan(A) = 11/5 and tan^-1(11/5) = A.
Since the sum of angles in a triangle is 180, we can find angle C by setting up this equation: C = 180 - 90 - tan^-1(11/5), which is 90 - tan^-1(11/5)
...............................................................

Answers
Answer:
a) 53.33 miles per hour
b) 1.7 pages per minute
c)2.25 $ per avocado
Step-by-step explanation:
a) 320/6 = 53.33333
b) 68/40 = 1.7
c) 27 /12 = 2.25
Least to greatest 34.039 32.94 34.198 32.102 33.6, 33.1
Answers
Answer:
32.102 < 32.94 < 33.1 < 33.6 < 34.039 < 34.198
Step-by-step explanation:
34.039, 32.94, 34.198, 32.102, 33.6, 33.1
32 < 33 < 34, so start by moving the two numbers beginning with 32 to the left, follow by the numbers with 33, then the numbers with 34.
Now compare the first digit to the right of the decimal point, the tenths digit.
32.102, 32.94, 33.1, 33.6, 34.039, 34.198
32.102 < 32.94 < 33.1 < 33.6 < 34.039 < 34.198
39. From the top of a vertical cliff 50 meters high, the angles of depression of an object that is levelled with
the base of the cliff is 30°. How far is the object from the base of the cliff?
A. 50 meters
B. 50-√3 meters
C. 100 meters
D. 100-√3 meters
40. What expression is used to answer: "A 4-m tall man stands on horizontal ground 43 m from a tree.
The angle of depression from the top of the tree to his eyes is 22°. Estimate the height of the tree."
A. sin 22
B. cos 22
C. tan 22
D. cot 22
41. From the top of the building of a food chain, the angle of depression from where Miguel stands is
45°. If the building is 12 meters high, how far is he from it?
A. 11 meters
B. 12 meters
C. 13 meters
D. 14 meters
42. A plane, at an altitude of 3,000 feet, observes the airport at an angle of 27°. What is the
horizontal distance between the plane and the airport to the nearest foot?
A. 3,000 feet
B. 4,000 feet
C. 5,000 feet
D. 6,000 feet
43. An escalator has an angle of elevation of 10° and a vertical rise of 6 m. Find the length of the
escalator.
C. 34.55 m
D. 36 m
A. 6,09 m
B. 34,03 m
Answers
Answer: cos4
Step-by-step explanation: 50 meters
B. 50-√3 meters
C. 100 meters
D. 100-√3 meters
40. What expression is used to answer: "A 4-m tall man stands on horizontal ground 43 m from a tree.
The angle of depression from the top of the tree to his eyes is 22°. Estimate the height of the tree."
A. sin 22
B. cos 22
C. tan 22
D. cot 22
Write a quadratic function to model the vertical motion for each situation, given h(t) equals negative 16t squared plus v0t+h0. Find the maximum height. Initial velocity 152
Answers
The maximum height reached by the ball is 908.5 feet.
Using the given values, we can substitute v0 = 152 and h0 = 6 into the equation:
\(h(t) = -16t^2 + 152t + 6\)
This quadratic function models the height of the ball at any time t after it is thrown.
To find the maximum height of the ball, we need to find the vertex of the parabolic curve described by the quadratic function. The vertex can be found using the formula:
t = -b / 2a
where a = -16 and b = 152 are the coefficients of the quadratic function.
t = -152 / 2(-16) = 4.75
So the maximum height is reached after 4.75 seconds. To find the maximum height, we can substitute this value back into the equation:
\(h(4.75) = -16(4.75)^2 + 152(4.75) + 6 = 908.5\)feet
Therefore, the maximum height reached by the ball is 908.5 feet.
for such more question on height
https://brainly.com/question/27987869
#SPJ11
Question
A ball is thrown vertically upward from a height of 6 feet with an initial velocity of 152 feet per second. Write a quadratic function to model the vertical motion of the ball, given that the height of the ball at time t is given by: h(t) = -16t^2 + v0t + h0
2
Let g(x) = x + 4x-7.
What is g(x) in graphing form?
(x + 2) - 7 = 4
O g(x) = (x + 2)²-7
Onone of the answer choices
x² + 4x-7=0
O g(x) = (x + 2)² - 11

Answers
The graphing form of the function g(x) is: C) none of the answer choices.
The function g(x) = \(x^2 + 4x - 7\)is already in the standard form of a quadratic equation. In graphing form, a quadratic equation can be represented as y =\(ax^2 + bx + c,\) where a, b, and c are constants.
Comparing the given function g(x) =\(x^2 + 4x - 7\)with the standard form, we can identify the coefficients:
a = 1 (coefficient of x^2)
b = 4 (coefficient of x)
c = -7 (constant term)
Therefore, the graphing form of the function g(x) is:
C) none of the answer choices
None of the given answer choices (A, B, D, or E) accurately represents the graphing form of the function g(x) =\(x^2 + 4x - 7\). The function is already in the correct form, and there is no equivalent transformation provided in the answer choices. The given options either represent different equations or incorrect transformations of the original function.
In graphing form, the equation y = \(x^2 + 4x - 7\) represents a parabolic curve. The coefficient a determines the concavity of the curve, where a positive value (in this case, 1) indicates an upward-opening parabola.
The coefficients b and c affect the position of the vertex and the intercepts of the curve. To graph the function, one can plot points or use techniques such as completing the square or the quadratic formula to find the vertex and intercepts. Option C
For more such questions on graphing visit:
https://brainly.com/question/19040584
#SPJ8
I need help with this question

Answers
9514 1404 393
Answer:
g(x) = x² -3
Step-by-step explanation:
There is no vertical scaling (a=1) or horizontal shift (h=0). The only shift is a down shift by 3 units (k=-3), so the transformed equation is ...
g(x) = x² -3
The figure shows four box-and-whisker plots. These represent variation in travel time for four different types of transportation from the beginning to the end of one route.
Conrad is at one end of the route. He is trying to decide how to get to an appointment at the other end. His appointment is in 30 minutes. Which type of transportation is LEAST likely to take more than 30 minutes?
Select one:
a.
bus
b.
car
c.
subway
d.
train

Answers
Comparing the median of each box-and-whisker plot, the type of transportation that is LEAST likely to take more than 30 minutes is: d. train.
How to Interpret a Box-and-whisker Plot?
In order to determine the transportation that is LEAST likely to take more than 30 minutes, we have to compare the median of each data set represented on the box-and-whisker plot for each transportation.
The box-and-whisker plot that has the lowest median would definitely represent the the transportation that is LEAST likely to take more than 30 minutes, since median represents the typical minutes or center of the data.
Therefore, from the box-and-whisker plots given, the one for train has the lowest median. Therefore train would LEAST likely take more than 30 minutes.
Learn more about box-and-whisker plots on:
brainly.com/question/27849170
#SPJ1
A package of 25 fishing hooks costs $9.95 , while a package with 40 hooks costs $13.99 . Which is the better buy? Round your answer to the nearest cent if necessary.
Answers
Therefore, the package with 40 hooks is the better buy in terms of cost efficiency.
To determine which package is the better buy, we need to compare the cost per hook for each package.
For the package of 25 hooks costing $9.95, we divide the total cost by the number of hooks:
Cost per hook = $9.95 / 25 = $0.398
Rounding to the nearest cent, the cost per hook is $0.40.
For the package of 40 hooks costing $13.99, we divide the total cost by the number of hooks:
Cost per hook = $13.99 / 40 = $0.3498
Rounding to the nearest cent, the cost per hook is $0.35.
Comparing the two costs per hook, we can see that the package with 40 hooks for $13.99 offers a better deal, as the cost per hook is lower at $0.35.
For such more question on package
https://brainly.com/question/12251427
#SPJ8
The surface area of a cube may be found using the formula A=6s^2. What is the edge length of a cube with a surface area of 81 cm^2? Round your answer to the nearest tenth.
Answers
Answer: s = 3.7 (rounded 3.67 to the nearest tenth)
Step-by-step explanation:
Surface Area = 81 cm^2
Surface Area of the cube = 6s^2
A = 6s^2
81 = 6s^2
S^2 = 81/6
S = 3.67
If you add Natalie's age and Fred's age, the result is 44. If you add Fred's age to 4 times
Natalie's age, the result is 83. Write and solve a system of equations to find how old Fred and Natalie
are
Answers
Answer: 31, 13
Step-by-step explanation:
You draw a rectangle with vertices at (-3.5,3), (3.5,3), (3.5,-3), and (-3.5,-3).
What is the perimeter and area of the rectangle?
Answers
The perimeter and the area of the rectangle are 26 units and 42 square units, respectively.
What is a rectangle?A rectangle is a quadrilateral with all four interior angles 90°.
Given that, the vertices of the rectangle are (-3.5,3), (3.5,3), (3.5,-3), and (-3.5,-3).
The length of the rectangle is:
l = 3.5 - (-3.5)
l = 3.5 + 3.5
l = 7
The width of the rectangle is:
w = 3-(-3)
w = 3 + 3
w = 6
The perimeter of the rectangle is given by:
P = 2 (l +w)
P = 2(7 + 6)
P = 26
The area of the rectangle is:
A = l × w
A = 7 × 6
A = 42
Hence, the perimeter and the area of the rectangle are 26 units and 42 square units, respectively.
Learn more on rectangles here:
https://brainly.com/question/15019502
#SPJ1
..A tin of paint was 2/3 litres full. Tom used 1/2 of
the paint to paint his table. How much was left ?
Answers
Multiply the amount of paint started with by the amount used:
2/3 x 1/2 = (2 x 1) / (3 x 2) = 2/6 = 1/3
There is 1/3 liter left
3s + 4 = -5 , what would the working be for this?
Answers
Answer:
-3
Step-by-step explanation:
3s + 4 = -5
3s + 4 - 4 = -5 - 4
3s = -9
3s/3 = -9/3
s = -3
Hope this is right
In analyzing this diagram, which statement represents a crucial step to proving the pythagorean theorem using this diagram?
A) The large square on the left contains two smaller squares
B) The large square on the right contains a smaller square with side length c
C) The perimeter of the blue square is equal to the perimeter of the yellow square.
D) Recognize that BOTH of the large squares contain 4 right triangles with base a and height b
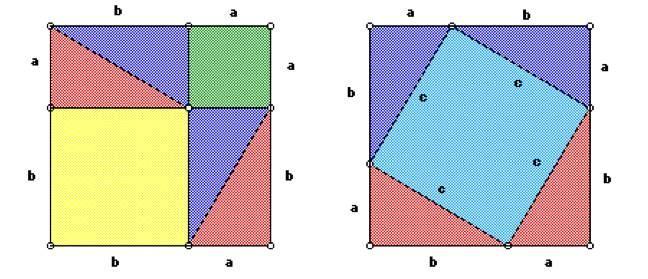
Answers
Answer:
D: recognize that BOTH of the large squares contain 4 right triangles with base a and height b
Step-by-step explanation:
Unions, intersections, and complements involving 2 sets
Sets B and C are subsets of the universal set U.
These sets are defined as follows.
U={f, k, m, s, x, y, z)
B={k, s, y}'
C={s,z}
(a) B'UC' = 1
(b) B'nc =
Answers
Intersection of B'∩C = {k, y}
To find the intersection of B' and C, we need to first find the complement of set B (B') and then find the intersection between B' and C.
1. Complement of set B (B'):
The complement of set B (B') consists of all elements in the universal set U that are not in set B. From the given information, set B is defined as {k, s, y}', which means it contains all elements in U except for k, s, and y. Therefore, the complement of set B is {f, m, x, z}.
2. Intersection between B' and C:
Now, we need to find the intersection between B' (complement of B) and set C. From the given information, set C is defined as {s, z}. To find the intersection, we need to identify the common elements between B' and C.
The elements present in both B' and C are k and y. Therefore, the intersection of B' and C is {k, y}.
So, the answer to (b) is B'∩C = {k, y}.
For more such questions on Intersection, click on:
https://brainly.com/question/30915785
#SPJ8
Choose the most reasonable unit of measure.
3) Area of a baseball infield: 925
A) mm² B) km² C) m² D) cm²
4) Area of a lake: 4
A) mm² B) km² C) m² D) cm²
5) Area of a door: 20
A) yd² B) in.² C) ft² D) mi²
Answers
The most reasonable unit of measurement for 3) is option (C): \(m^2\), 4) is option (B): \(km^2\), 5) is \(in^2\).
3) The most reasonable unit for the measurement of the baseball field is \(m^2\) because the baseball field covers a large distance which is not accurately measured by small units \(cm^2\) or \(mm^2\) where it is not that big to be measured in large units like \(km^2\). So option C is the correct option.
4) The most reasonable unit for the measurement of a lake is \(km^2\) because lakes are generally very large water bodies that cover a large distance and are not accurately measured by small units like \(cm^2\) , \(mm^2\) , and \(m^2\). So option B is the correct option.
5) The most reasonable unit for the measurement of the area of a door is \(in^2\) because doors are relatively small compared to the other options and are often measured in square inches or square feet. So option B is the correct option.
Therefore the correct answers question-wise are:
3) \(m^2\)
4) \(km^2\)
5) \(in^2\)
Learn more about the unit of measurement at:
https://brainly.com/question/30644235
#SPJ1
1. Show using the preimage theorem that the tangent space to the Stiefel manifold of orthonormal 2 -frames inRnat a point[v1,v2], is the vector space of vectors(u,w)∈Rn×Rnsatisfyingv1⋅uv2⋅wv1⋅w+v2⋅u=0=0=0.
Answers
As a result, the set of all [u, w] Rn Rn satisfying the previous equation is the tangent space to F at [v1, v2] by using preimage theorem.
Let F be the Stiefel manifold of orthonormal 2-frames in Rn to apply the preimage theorem. The collection of all tangent vectors to curves passing through [v1, v2] in F is what is known as the tangent space T[F] at a location [v1, v2]. Let (t) be a straight line in F such that (v1, v2) is a smooth curve. The tangent vector to t at time t = 0 is then given by
γ′(0) = [u, w] ∈ T[F].
We must now determine the requirements that [u, w] must meet in order to be in T[F]. Assume that V is a matrix with columns named v1 and v2. If Q is an orthogonal matrix, then any orthonormal 2-frame [v1′, v2′] in Rn can be represented as VQ. The category to which [v1′, v2′] belong Q is a 2 by 2 matrix with determinant 1, and F is equivalent to Q. Given that Q(0) = I, let Q(t) be a smooth curve in SO(2). Then, there is
γ(t) = VQ(t) (t),
and
γ′(0) = VQ′(0) (0).
We have Q since Q(t) is orthogonal (t)
TQ(t) = I, indicating
Q′(0)T + Q′(0) = 0.
Let [u, w] T[F] now. Once this is the case, a smooth curve Q(t) in SO(2) exists with Q(0) = I and
[u, w] = VQ′(0) (0).
Applying the equation above, we obtain
v1uv2w plus v1wv2u equals 0.
As a result, the set of all [u, w] Rn Rn satisfying the previous equation is the tangent space to F at [v1, v2].
to know more about" theorem" at https://brainly.com/question/343682
#SPJ4
A sum amount
to rupees 34476 in two and a half years at 4% CI. the sum is
Answers
Given:
Amount = Rs. 34476
Rate of compound interest = 4%
Time = \(2\dfrac{1}{2}=2.5\) years
To find:
The principal value.
Solution:
Formula for amount is
\(A=P\left(1+\dfrac{r}{100}\right)^t\)
Where, P is principal value, r is rate of interest and t is time in years.
Putting the given values, we get
\(34476=P\left(1+\dfrac{4}{100}\right)^{2.5}\)
\(34476=P\left(1+0.04\right)^{2.5}\)
\(34476=P\left(1.04\right)^{2.5}\)
\(\dfrac{34476}{\left(1.04\right)^{2.5}}=P\)
Now,
\(P=31256.0090\)
\(P\approx 31256\)
Therefore, the value of sum or principal value is Rs.31256.
(a) Copy and complete the table of values for y= 2x²-x-4 for-3 ≤x≤3.
X
y
-3
17
-2 -1
0
(c) Use the graph to find the:
-4
1
2 3
(b) Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 units on the y-axis,
draw the graph of y=2x²-x-4 for -3 ≤x≤3.
(i) roots of the equation 2x2-x-4 = 0;
(ii) values of x for which y increases as x increases,
(iii) minimum point of y.
Answers
The minimum point of y is (0, -4).
X | y
-3 | 17
-2 | -4
-1 | -7
0 | -4
1 | -1
2 | 4
3 | 11
Using these values, we can proceed with the requested tasks:
(b) To draw the graph of y = 2x² - x - 4, we will use a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 units on the y-axis. Here's how the graph looks:
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
----+---+---+---+---+---+---+--
-3 -2 -1 0 1 2 3
The graph will have a parabolic shape, opening upward.
(i) To find the roots of the equation 2x² - x - 4 = 0, we need to find the x-values where the graph intersects the x-axis. From the graph, we can see that the roots are approximately x = -2 and x = 1. These are the values where the graph crosses the x-axis.
(ii) To find the values of x for which y increases as x increases, we need to identify the intervals on the x-axis where the graph is moving upwards. From the graph, we can see that as x increases from -3 to -2, and from 1 to 3, y is increasing. Therefore, the values of x for which y increases as x increases are x ∈ (-3, -2) and x ∈ (1, 3).
(iii) To find the minimum point of y, we need to locate the vertex of the parabolic graph. From the graph, we can see that the vertex is approximately at x = 0, y = -4. Therefore, the minimum point of y is (0, -4).
For more questions on minimum point
https://brainly.com/question/30236354
#SPJ8
Factor the quadratic expression completely.
-3x^2+17x-20=
Answers
Answer:
To factor -3x^2 + 17x - 20 completely, we need to find two binomials that when multiplied together give us the original quadratic expression.
First, we can multiply the leading coefficient (-3) by the constant term (-20) to get -60. Then, we need to find two numbers that multiply to -60 and add up to the coefficient of the x-term (17). After some trial and error, we find that the two numbers are 12 and -5.
Now, we can rewrite the quadratic expression as:
-3x^2 + 17x - 20 = -3x^2 + 12x - 5x - 20
Next, we group the first two terms and the last two terms:
(-3x^2 + 12x) + (-5x - 20)
We can factor out 3x from the first group and -5 from the second group:
3x(x - 4) - 5(x + 4)
Now we can factor out a negative one from the second grouping:
3x(x - 4) - 5( -1)(x + 4)
And simplify:
3x(x - 4) + 5(x + 4)
Therefore, the quadratic expression -3x^2 + 17x - 20 can be factored completely as (3x - 5)(x - 4).
Casey buys a bracelet. She pays for the bracelet and pays $0.72 sales tax. The sales tax rate is 6%, percent.
What is the original price of the bracelet, before tax?
Answers
Answer:
12$
Step-by-step explanation: 100/6 then multiply it by .72=12$
Answer
$12
Step-by-step explanation:
theres a picture on how I did it that I linked.

