Answers
Answer:
\(XY=2YZ\\XY=2\times4\\XY=8\)
The value of XY is given by the trigonometric relation and the measure of side of the triangle is XY = 8
What are trigonometric relations?Trigonometry is the study of the relationships between the angles and the lengths of the sides of triangles
The six trigonometric functions are sin , cos , tan , cosec , sec and cot
Let the angle be θ , such that
sin θ = opposite / hypotenuse
cos θ = adjacent / hypotenuse
tan θ = opposite / adjacent
tan θ = sin θ / cos θ
cosec θ = 1/sin θ
sec θ = 1/cos θ
cot θ = 1/tan θ
Given data ,
Let the triangle be represented as XYZ
Let the measure of the side XY of the triangle be A
The measure of side YZ = 4
Now , from the trigonometric relations , we get
sin θ = opposite / hypotenuse
when θ = 30°
Substitute the value of θ in the equation , we get
sin θ = YZ / XY
On simplifying the equation , we get
sin 30° = 4 / XY
Multiply by XY on both sides of the equation , we get
XY ( sin 30° ) = 4
The value of sin 30° = 1/2
So , XY / 2 = 4
Multiply by 2 on both sides of the equation , we get
XY = 8
Hence , the measure of side XY of triangle is XY =8
To learn more about trigonometric relations click :
https://brainly.com/question/14746686
#SPJ2
Related Questions
Find the experimental probability of tossing heads.
H stands for heads and T stands for Tails.
Coin Toss Results: T, H, T, H, T, H, T, T, T, T, H, T, H, T, T
Answers
The value of the experimental probability of tossing heads is,
⇒ 1 / 3
We have to given that;
Coin Toss Results: T, H, T, H, T, H, T, T, T, T, H, T, H, T, T
Where, H stands for heads and T stands for Tails.
Hence, Total outcomes = 15
And, Head outcomes = 5
Thus, The value of the experimental probability of tossing heads is,
⇒ 5 / 15
⇒ 1 / 3
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
Which expression is equivalent to 1/2 x + (-70) - 2 1/4 x - (-2) *
Answers
Answer:
-7/4x-68
Step-by-step explanation:
the slope of (3, 12) and (4, 16)
Answers
Answer:it’s 1/4
Step-by-step explanation:
Find all values of m for which the equation has two real solutions.
3x² + 7x- (m + 1) = 0

Answers
A restaurant has 23 tables. Some of the tables seat 4 persons and the rest seat two persons. In all, 76 persons can be seated at once. How many tables of each kind are there?
Answers
Answer:
15 tables with 4 seats and 8 tables with 2 seats.
Step-by-step explanation:
x = 4 seated tables
y = 2 seated tables
x + y = 23
4x + 2y = 76
Multiply first equation by -2 to cancel y's:
-2x - 2y = -46
4x + 2y = 76
2x = 30
x = 30 / 2
x = 15
And we said 23 tables so:
23 - 15 = 8
x = 15
y = 8
To factor 4x^2-25, you can first rewrite the expression as:
a. (2x-5)^2
b. (2x)^2-(5)^2
c. (x)^2-(2)^2
d. None of the above
Answers
To factor the expression 4x^2 - 25, we can use the difference of squares formula, which states that a^2 - b^2 can be factored as (a + b)(a - b).
In this case, we have 4x^2 - 25, which can be written as (2x)^2 - 5^2. Comparing it with the difference of squares formula, we can identify that a = 2x and b = 5. Therefore, the correct option is:
b. (2x)^2 - (5)^2
Using the difference of squares formula, we can factor it as follows:
(2x + 5)(2x - 5)
Hence, the correct factorization of 4x^2 - 25 is (2x + 5)(2x - 5), which is equivalent to option b.
For such more question on factor
https://brainly.com/question/24351176
#SPJ8
A coin having probability p=2/3 of coming up heads is flipped 6 times. Compute the entropy of the outcome of this experiment.
Answers
The entropy of the outcome of this experiment = 9
A probability is a number that reflects the chance or likelihood that a particular event will occur. Probabilities can be expressed as proportions that range from 0 to 1, and they can also be expressed as percentages ranging from 0% to 100%.
Given that,
A coin having probability p=2/3
Heads is flipped 6 times
If the coin is flipped 6 times
The Total Number of Trial in the Experiment =2/3
It comes up heads 6 times
This Means: Number of Successful Outcome of HEADS =6
In an experimental probability,
Experimental probability of the coin’s coming up heads
=Number of Successful Outcome of HEADS/Total Number of Trials in the Experiment
= 6/(2/3)
= 6*3/2
= 18/2
= 9
Therefore,
The entropy of the outcome of this experiment = 9
To learn more about of Probability visit :
brainly.com/question/29509157
#SPJ4
Two cars leave towns 680 kilometers apart at the same time and travel toward each other. One car's rate is 16 kilometers per hour less than the other's. If they
meet in 4 hours, what is the rate of the slower car?
Do not do any rounding.
Answers
The rate of the slower car is 77km/hr
What is velocity?Velocity is the rate of change of displacement with time. It is measured in meter per second and it is a vector quantity.
velocity = displacement/time
displacement = velocity × time
represent the faster car by v1 and the slower car by v2
v1 = v2+16
V2 = v1-16
Total displacement = 680km
680 =( v1+V2)t
680 = (v1+V2)4
v1+v2 = 680/4
v2+16+v2 = 170
2v2 = 170-16
2v2 = 154
v2 = 154/2
v2 = 77km/hr
therefore the rate of the slower car is 77km/hr
learn more about velocity from
https://brainly.com/question/80295
#SPJ1
Suppose a geyser has a mean time between irruption’s of 75 minutes. If the interval of time between the eruption is normally distributed with a standard deviation 20 minutes, answer the following questions. (A) What is the probability that a randomly selected Time interval between irruption’s is longer than 84 minutes? (B) what is the probability that a random sample of 13 time intervals between irruption‘s has a mean longer than 84 minutes? (C) what is the probability that a random sample of 20 time intervals between irruption‘s has a mean longer than 84 minutes? (D) what effect does increasing the sample size have on the probability? Provide an exclamation for this result. Choose the correct answer below. (E) what might you conclude if a random sample of 20 time intervals between irruption‘s has a mean longer than 84 minutes? Choose the best answer below. I’m not entirely certain about my answer for a bit I am completely and utterly lost on the other questions... please help.
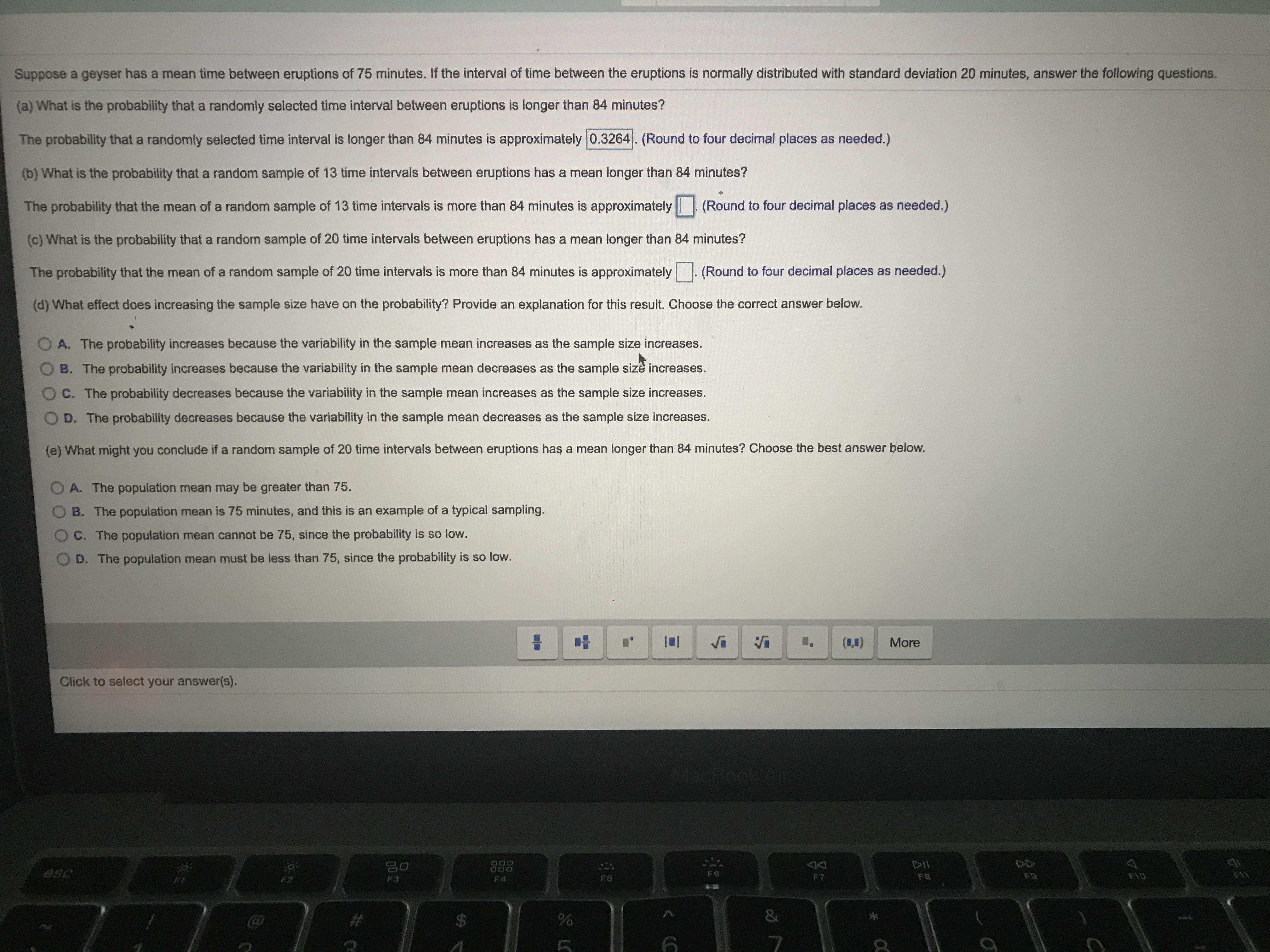
Answers
Answer:
(a) The probability that a randomly selected Time interval between irruption is longer than 84 minutes is 0.3264.
(b) The probability that a random sample of 13 time intervals between irruption has a mean longer than 84 minutes is 0.0526.
(c) The probability that a random sample of 20 time intervals between irruption has a mean longer than 84 minutes is 0.0222.
(d) The probability decreases because the variability in the sample mean decreases as we increase the sample size
(e) The population mean may be larger than 75 minutes between irruption.
Step-by-step explanation:
We are given that a geyser has a mean time between irruption of 75 minutes. Also, the interval of time between the eruption is normally distributed with a standard deviation of 20 minutes.
(a) Let X = the interval of time between the eruption
So, X ~ Normal(\(\mu=75, \sigma^{2} =20\))
The z-score probability distribution for the normal distribution is given by;
Z = \(\frac{X-\mu}{\sigma}\) ~ N(0,1)
where, \(\mu\) = population mean time between irruption = 75 minutes
\(\sigma\) = standard deviation = 20 minutes
Now, the probability that a randomly selected Time interval between irruption is longer than 84 minutes is given by = P(X > 84 min)
P(X > 84 min) = P( \(\frac{X-\mu}{\sigma}\) > \(\frac{84-75}{20}\) ) = P(Z > 0.45) = 1 - P(Z \(\leq\) 0.45)
= 1 - 0.6736 = 0.3264
The above probability is calculated by looking at the value of x = 0.45 in the z table which has an area of 0.6736.
(b) Let \(\bar X\) = sample time intervals between the eruption
The z-score probability distribution for the sample mean is given by;
Z = \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) ~ N(0,1)
where, \(\mu\) = population mean time between irruption = 75 minutes
\(\sigma\) = standard deviation = 20 minutes
n = sample of time intervals = 13
Now, the probability that a random sample of 13 time intervals between irruption has a mean longer than 84 minutes is given by = P(\(\bar X\) > 84 min)
P(\(\bar X\) > 84 min) = P( \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) > \(\frac{84-75}{\frac{20}{\sqrt{13} } }\) ) = P(Z > 1.62) = 1 - P(Z \(\leq\) 1.62)
= 1 - 0.9474 = 0.0526
The above probability is calculated by looking at the value of x = 1.62 in the z table which has an area of 0.9474.
(c) Let \(\bar X\) = sample time intervals between the eruption
The z-score probability distribution for the sample mean is given by;
Z = \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) ~ N(0,1)
where, \(\mu\) = population mean time between irruption = 75 minutes
\(\sigma\) = standard deviation = 20 minutes
n = sample of time intervals = 20
Now, the probability that a random sample of 20 time intervals between irruption has a mean longer than 84 minutes is given by = P(\(\bar X\) > 84 min)
P(\(\bar X\) > 84 min) = P( \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) > \(\frac{84-75}{\frac{20}{\sqrt{20} } }\) ) = P(Z > 2.01) = 1 - P(Z \(\leq\) 2.01)
= 1 - 0.9778 = 0.0222
The above probability is calculated by looking at the value of x = 2.01 in the z table which has an area of 0.9778.
(d) When increasing the sample size, the probability decreases because the variability in the sample mean decreases as we increase the sample size which we can clearly see in part (b) and (c) of the question.
(e) Since it is clear that the probability that a random sample of 20 time intervals between irruption has a mean longer than 84 minutes is very slow(less than 5%0 which means that this is an unusual event. So, we can conclude that the population mean may be larger than 75 minutes between irruption.
Write a linear function for the graph, and state and interpret the slope and y-intercept for the given scenario:
Bamboo grows very quickly. Use the information in the graph to write an equation that models the height (y) at time (x).
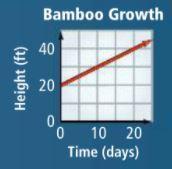
Answers
The linear function for the given graph is y = x + 20.
What is a linear function?
A straight line on the coordinate plane is represented by a linear function. It has one independent variable and one dependent variable. For slope (m) and y-intercept (b) form, the equation is given by:
y = mx + b
From the graph,
The coordinates of the given graph are (0,20) and (20,40)
Then, slope (m) = (40-20)/(20-0) = 20/20 = 1
and y-intercept (b) = 20
So, the equation will be y = 1x + 20
Hence, the linear function for the given graph is y = x + 20.
To learn more about a linear function
https://brainly.com/question/29213103
#SPJ1
7. Mrs. Paulson is constructing a 90% confidence interval for the difference of means based on independent
simple random samples from two populations. The sample sizes are n, = 6 and n, =14. She draws dotplots
of the sample data to check one of the conditions for using two-sample i procedures. Which of the following
descriptions of those dotplots would suggest that it is safe to perform inference?
(a) Both dotplots are roughly symmetric. There are no outliers in either dotplot.
(b) Both dotplots are roughly symmetric. The dotplot of sample 2 has an outlier.
(c) Both dotplots are strongly skewed to the right. There are no outliers in either dotplot.
(d) Both dotplots are roughly symmetric. Both dotplots have one upper outlier
(e) i procedures are not recommended in any of these cases.
Answers
The description that will show that it is safe to perform inference is that (a) Both dotplots are roughly symmetric. There are no outliers in either dotplot.
What description would make it possible to make inferences?In order to use the two-sample t procedure to make inferences, certain conditions need to be met such as the sample being random and independent.
The variances for the groups in the data need to be equal which is why the presence of no outliers in either dotplot would present an safe opportunity to be able to perform inferences on the data.
In conclusion, option A is correct.
Find out more on two-sample t-tests at https://brainly.com/question/17438355.
A team of researchers wants to determine whether pet owners are generally more satisfied with their lives than non-pet owners. To test their theory, the researchers randomly select 500 pet owners and 500 non-pet owners from several major metropolitan areas in the country. The researchers then interview the individuals, asking them a series of questions. Each response is assessed with a point value that is later translated to a satisfaction indicator. Of the pet owners surveyed, 380 of the 500 were found to be satisfied with their lives, while 336 of the 500 non-pet owners were found to be satisfied.
Would this study be considered an experiment or an observational study?
Answers
Answer:
observational study
Step-by-step explanation:
Task 3 Instructions and information The original triangle has an area equal to 729 small dotty triangles. This can be checked by counting, but there is a more efficient way. Notice that the small dotty triangles in the original triangle form rows of triangles. The first row, at the top of the triangle has I small triangle. • The second row has 3 triangles How triangles are there in the 3rd and 4th rows? n How many rows are there? Use your knowledge of series to check the total number of small triangles in the original triangle.
Answers
If the original triangle has an area equal to 729 small dotty triangles. The original triangle has an area of 8 square units.
How to find the original triangle?Let's first find the pattern of the number of small triangles in each row. The first row has 1 small triangle. The second row has 3 small triangles. The third row has 5 small triangles, and the fourth row has 7 small triangles. We can see that the pattern is that each row has 2 more small triangles than the previous row.
To find how many small triangles are in the third row, we add 2 to the number of small triangles in the second row:
3 + 2 = 5
So there are 5 small triangles in the third row.
To find how many small triangles are in the fourth row, we add 2 to the number of small triangles in the third row:
5 + 2 = 7
So there are 7 small triangles in the fourth row.
To find the total number of rows, we can count the number of rows from the top of the triangle to the bottom. Alternatively, we can use the formula for the sum of an arithmetic series to find the number of terms in the sequence. In this case, the first term is 1, the common difference is 2, and the last term is 7. Using the formula:
n = (last term - first term) / common difference + 1
n = (7 - 1) / 2 + 1
n = 4
So there are 4 rows in the triangle.
Finally, we can use the formula for the sum of an arithmetic series to find the total number of small triangles in the original triangle. In this case, the first term is 1, the common difference is 2, and the number of terms is 4. Using the formula:
sum = (n / 2) * (first term + last term)
sum = (4 / 2) * (1 + 7)
sum = 4 * 4
sum = 16
So there are 16 small triangles in the original triangle. Since each small triangle has an area of 1/2, the total area of the original triangle is:
area = 16 * (1/2)
area = 8
Therefore, the original triangle has an area of 8 square units.
Learn more about triangle here:https://brainly.com/question/17335144
#SPJ1
PLEASE HELP D:
What is the area of a triangle that has a height of 10 feet and a base length of 8 feet?
A - 10 feet^2
B - 20 feet^2
C - 40 feet^2
D - 80 feet^2
Answers
Answer:
C. 40 ft²Step-by-step explanation:
Triangle area formula:
A = bh/2, where b- base, h- heightWe have:
b = 8 ft, h = 10 ftThe area is:
A = 8*10/2 = 40 ft²Correct choice is C
Jenny earns $30 a day working part time at a supermarket. Write an expression to represent the amount of money she will earn in d days.
Answers
Answer: d($30)
Explanation: $30 times d which d is the number of days.
OMG PLZZZZ HELP ME!! I NEED DA ASMWER ASAP!!

Answers
Answer:
I am not sure but I would say rectangular prisim
Step-by-step explanation:
HELP!!!!!!!! Which system of linear equations can be solved using the information below?

Answers
The system of linear equations that can be solved from the matrices is given as follows:
-5x + 4y = 3.-8x + y = -6.How to obtain the system of equations?Considering that the row [3, -6] is common to matrices Ax and Ay, the matrix A is given as follows:
A = [-5 4; -8 1]
Hence the multiplication of matrices representing the system is given as follows:
[-5 4; -8 1][x; y] = [3; -6]
Applying the multiplication of matrices, the system of equations is given as follows:
-5x + 4y = 3.-8x + y = -6.More can be learned about a system of equations at https://brainly.com/question/13729904
#SPJ1
1 in a school test consisting of 10 questions, 5 points are awarded for a correct answer but 3 points are deducted for an incorrect answer. a blank answer scores 0. mike scored a total of 0 and he did not leave all of the answers blank
Answers
a) Either 3 or 4 questions did Mike answer correctly.
b) Either 7 or 8 questions did Sheila answer correctly.
What is a equation in math?In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal. For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an 'equal' sign.
a) Let mike did x correct
then, incorrect will be (10- x)
The equation is:
Now, 5x + (10 - x) (-3) = 0
=> 5x - 30 + 3x = 0
=> 8x = 30
=> x = 30/8
=> x > 3 and x < 4
b) Let Sheila did y correct
then, incorrect = (10 - y)
Now, 5y + (10 - y) (-3) = 32
=> 5y - 30 + 3y = 32
=> 8y = 62
=> y > 7 and y< 8
Learn more about Equation at:
https://brainly.com/question/29657992
#SPJ4
The given question is incomplete, complete question is:
In a school test consisting of 10 questions, 5 points are awarded for a correct answer but 3 points are deducted for an incorrect answer.
A blank answer scores (). Mike scored a total of () and he did not leave all of the answers blank. (a) How many questions did Mike answer correctly? _ _ _ _ _ _ _ _ Sheila scored a total of 32. (b) How many questions did Sheila answer correctly?
Suppose x is a random variable best described by a uniform probability distribution with c = 10 and d = 70. Find P(x < 25).
Answers
If you're talking about a discrete distribution, then
\(P(X=x)=\begin{cases}\frac1{61}&\text{for }x\in\{10,11,12,\ldots,70\}\\0&\text{otherwise}\end{cases}\)
(1/61 because there are 61 numbers in the range of integers from 10 to 70) so that
\(P(X<25)=\displaystyle\sum_{x=10}^{24}P(X=x)=\boxed{\dfrac{15}{61}}\)
If the distribution is continuous, we would have the same density function, but x can be any real number in the interval [10, 70]. So we have
\(P(X<25)=\displaystyle\int_{-\infty}^{25}P(X=x)\,\mathrm dx=\frac1{60}\int_{10}^{25}\mathrm dx=\dfrac{15}{60}=\boxed{\dfrac14}\)
h e l p m e please its 20 points

Answers
Answer:
its just a rotation. its as simple as rotating it back to its origonal form and matching up the corners
Step-by-step explanation:
help.........................

Answers
Answer:
32,64,128
Step-by-step explanation:
previous number × 2
Which linear function has the same y-intercept as the one that is represented by the graph?
On a coordinate plane, a line goes through points (3, 4) and (5, 0).
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 3, negative 1, 1, 3. Column 2 is labeled y with entries negative 4, 2, 8, 14.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 4, negative 2, 2, 4. Column 2 is labeled y with entries negative 26, negative 18, negative 2, 6.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 5, negative 3, 3, 5. Column 2 is labeled y with entries negative 15, negative 11, 1, 5.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 6, negative 4, 4, 6. Column 2 is lab
eled y with entries negative 26, negative 14, 34, 46.
Answers
The linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
To determine the linear function with the same y-intercept as the graph, we need to find the equation of the line passing through the points (3, 4) and (5, 0).
First, let's find the slope of the line using the formula:
slope (m) = (change in y) / (change in x)
m = (0 - 4) / (5 - 3)
m = -4 / 2
m = -2
Now that we have the slope, we can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Using the point (3, 4) as our reference point, we have:
y - 4 = -2(x - 3)
Expanding the equation:
y - 4 = -2x + 6
Simplifying:
y = -2x + 10
Now, let's check the given options to find the linear function with the same y-intercept:
Option 1: The table with x-values (-3, -1, 1, 3) and y-values (-4, 2, 8, 14)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 2: The table with x-values (-4, -2, 2, 4) and y-values (-26, -18, -2, 6)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 3: The table with x-values (-5, -3, 3, 5) and y-values (-15, -11, 1, 5)
The y-intercept is the same as the given line (10). So, this option is correct.
Option 4: The table with x-values (-6, -4, 4, 6) and y-values (-26, -14, 34, 46)
The y-intercept is not the same as the given line. So, this option is not correct.
Therefore, the linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
for such more question on linear function
https://brainly.com/question/9753782
#SPJ8
Find the equivalent fraction of 2/6, show the equivalent fractions on the number lines.

Answers
In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
2/6
equivalent fraction = ?
Step 02:
number line
\(\frac{2\text{ /2}}{6\text{ /2}}\text{ = }\frac{1}{3}\)The equivalent fraction in the number line is 1 /3 .
The answer is:
The equivalent fraction in the number line is 1 /3 .

Use this formula to calculate compound interest:
Principal x (1 + Interest Rate)(Time)
$100
Interest Rate = 4%
Time= 5 years
Using the information above, how much money would you have after 5 years? Choose the answer that is closest to the exact answer.
Answers
The amount after 5 years on $100 using the compound interest is $122.
According to the question,
We have the following information:
Principal = $100
Interest Rate = 4%
Time= 5 years
We know that the following formula is used to find the total amount if there is compound interest:
Compound amount = \(P(1+\frac{r}{100})^{t}\) where P is the principal, r is interest rate and t is the time in years
(Note that there are different formulas for compound interest depending on how it is calculated.)
A = \(100(1+\frac{4}{100})^{5}\)
A = \(100(\frac{104}{100})^{5}\\100(1.04})^{5}\)
A = 100*1.22
A = $122
Hence, the amount after 5 years on $100 using the compound interest is $122.
To know more about compound interest here
https://brainly.com/question/12106357
#SPJ1
Determine the value c so that each of the following functions can serve as a probability distribution of the discrete random variable X:(a) f(x) = c(x2 + 4), for x = 0, 1, 2, 3;(b) f(x) = c (2x) (33-x) , for x = 0, 1, 2. 2.^^(2 is supposed to be directly above x, but not in fraction form, same for 3 and 3-x)
Answers
The value of c is 1/17.
What is Probability?It is a branch of mathematics that deals with the occurrence of a random event.
Here it is given that the function f(x) can serve as a probability distribution of the discrete random variable X when f(x) = c(x² + 4), for x = 0, 1 ,2
We have to find the value of c
Since f(x) represents the probability distribution x = 0, 1 ,2
So we have f(0)+f(1)+f(2)=1
c(0²+4)+c(1²+4)+c(2²+4)=1
4c+5c+8c=1
17c=1
Divide both sides by 17
c=1/17
Hence, the value of c is 1/17.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ1
Determine the value c so that each of the following function can serve as a probability distribution of the discrete random variable X when f(x)=c(x2+4), for x=0, 1,2?
a.
1/3
b.
1/17
c.
1/2
d.
1/13
Complete the square to factorise x^2+4x-6
Answers
SOMEBODY PLS HELP ME <3

Answers
\(\boxed{\sf Slope=m=tan\Theta=\dfrac{y_2-y_1}{x_2-x_1}}\)
Looking at options
#A
\(\\ \sf\longmapsto m=\dfrac{3}{-3}=-1\)
Negative slope#B
\(\\ \sf\longmapsto m=tan\Theta=tan0=0\)
omitted#C
Line parallel to y axis hence any points have same x co-ordinate for which the x_2-x_1=0\(\\ \sf\longmapsto m=tan90=\infty\)
omitted#D
\(\\ \sf\longmapsto m=\dfrac{3}{3}=1\)
Positive slopeHence option D is correct
Answer:
• The first graph.
→ Consinder points (-2, 0) and (-3, -1) from the graph:
\({ \tt{slope = \frac{y _{2} - y _{1} }{x _{2} - x _{1} } }} \\ \\ { \tt{slope = \frac{0 - ( - 1)}{ - 2 - ( - 3)} = \frac{1}{1} }} \\ \\ { \boxed{ \tt{slope = {}^{ + } 1}}}\)

Fraser scores 43% in a spelling test. What percentage did he get wrong?
Answers
Answer:
100-43= 57
Explanation:
So, Frazer did 57% wrong
Answer:
57% incorrect wow he should have studied better lol ;)
Step-by-step explanation:
If he SCORED 43%, than out of 100% the remaining is 57%
The sum of two numbers is 4 1/2. The difference is 3 1/4. Find the numbers.
Answers
Answer:
let the two number is x and y
x + y = 4 1/2 .....(i)
x - y = 3 1/4 ......(ii)
adding question (i) and (ii)
x + y = 9/2
x - y = 31/4
=> 2x = 31/4
x = 8/31
substituting the value x in equation 1
8/31 + y = 9/ 2
y = 9/2 - 8/31
y =203/62
the value of x = 8/31
y = 203/62
The equation y-20000(0.95)* represents the purchasing power of $20,000, with an inflation rate of five percent. X represents the
number of years
Use the equation to predict the purchasing power in five years.
Round to the nearest dollar.
$15,476
$17,652
$18,523
$19,500
Answers
The purchasing power in five years will be $15,476.
To predict the purchasing power in five years, we can substitute the value of X as 5 into the equation y = 20000(0.95)^X.
Plugging in X = 5, we have:
\(y = 20000(0.95)^5\)
Calculating the expression, we find:
\(y ≈ 20000(0.774)\)
Simplifying further, we get:
\(y ≈ 15480\)
Rounding the result to the nearest dollar, the predicted purchasing power in five years would be approximately $15,480.
Therefore, the closest option to the predicted purchasing power in five years is $15,476.
So the correct answer is:
$15,476.
For more questions on purchasing
https://brainly.com/question/27975123
#SPJ8
Rounding to the nearest dollar, the predicted purchasing power in five years is approximately $15,480.
To predict the purchasing power in five years using the given equation, we substitute the value of x (representing the number of years) as 5 and calculate the result.
The equation provided is: y = 20000(0.95)^x
Substituting x = 5 into the equation, we have:
y = 20000(0.95)⁵
Now, let's calculate the result:
y ≈ 20000(0.95)⁵
≈ 20000(0.774)
y ≈ 20000(0.774)
≈ 15,480
This means that, according to the given equation, the purchasing power of $20,000, with an inflation rate of five percent, would be predicted to be approximately $15,480 after five years.
By changing the value of x (representing the number of years) to 5, we can use the preceding equation to forecast the buying power in five years.
The example equation is: y = 20000(0.95)^x
When x = 5 is substituted into the equation, we get y = 20000(0.95).⁵
Let's now compute the outcome:
y ≈ 20000(0.95)⁵ ≈ 20000(0.774)
y ≈ 20000(0.774) ≈ 15,480
This indicates that based on the equation, after five years, the purchasing power of $20,000 would be estimated to be around $15,480 with a five percent inflation rate.
For similar questions on purchasing power
https://brainly.com/question/3794707
#SPJ8
